Rep:Mod:ht309mod3

3rd Year Computational Labs: Physical

The Cope Rearrangement Tutorial

Introduction

In this investigation the low-energy minima and the transition structures of 1,5-hexadiene were located to determine the preferred reaction mechanism for the Cope Rearrangement, i.e. [3,3]-sigmatropic shift rearrangement using Gaussian. Literature reports the mechanism to proceed via an aromatic loose-chair transition state, i.e. a concerted transition state.

Optimisation of 1,5-Hexadiene

At first, several conformers of 1,5-hexadiene were assessed on GaussView using the HF/3-21g method and basis set. These conformers readily interconvert via free rotation of C-C σ bonds at room temperature. As well as optimising the conformers, the energy of the conformers were determined.

Raw Gaussian Data

Conformer	Structure	Point Group	Energy (HF/3-21G)/Eh	Energy (DFT/B3LYP/6-)/Eh	Σ(Eelec + ZPE)/Eh	Σ(Eelec + Etherm)/Eh	Σ(Helec + Htherm)/Eh	Σ(Gelec + Gtherm)/Eh	DOI (freq.log)
Anti 1		C2	-231.69260	-234.61180	-234.46929	-234.46197	-234.46102	-234.50016	DOI:10042/to-10028
Anti 2		Ci	-231.69254	-234.61170	-234.46921	-234.46186	-234.46091	-234.50082	DOI:10042/to-10024
Anti 3		C2h	-231.68907	-234.60964	-234.46699	-234.45982	-234.45887	-234.49734	DOI:10042/to-10029
Anti 4		C1	-231.69097	-234.61079	-234.46819	-234.46094	-234.46000	-234.49948	DOI:10042/to-10027
Gauche 1		C2	-231.68772	-234.60788	-234.46525	-234.45812	-234.45718	-234.49548	DOI:10042/to-10025
Gauche 2		C2	-231.69167	-234.61070	-234.46821	-234.46094	-234.45600	-234.49910	DOI:10042/to-10070
Gauche 3		C1	-231.69266	-234.61133	-234.46849	-234.46146	-234.46052	-234.50011	DOI:10042/to-10030
Gauche 4		C2	-231.69153	-234.61048	-234.46778	-234.46052	-234.45958	-234.49869	DOI:10042/to-10031
Gauche 5		C1	-231.68962	-234.60911	-234.46637	-234.45921	-234.45827	-234.49744	DOI:10042/to-10057
Gauche 6		C1	-231.68916	-234.60889	-234.46628	-234.45910	-234.45816	-234.49737	DOI:10042/to-10032

DOI: Energies

Conformation	DOI
Anti 1	HF/3-21GDOI:10042/to-10077 DFT/B3LYP/6-31G*DOI:10042/to-10026
Anti 2	HF/3-21GDOI:10042/to-10072 DFT/B3LYP/6-31G*DOI:10042/to-10075
Anti 3	HF/3-21GDOI:10042/to-10080 DFT/B3LYP/6-31G*DOI:10042/to-10071
Anti 4	HF/3-21GDOI:10042/to-10078 DFT/B3LYP/6-31G*DOI:10042/to-10079
Gauche 1	HF/3-21GDOI:10042/to-10074 DFT/B3LYP/6-31G*DOI:10042/to-10073
Gauche 2	HF/3-21GDOI:10042/to-10090 DFT/B3LYP/6-31G*DOI:10042/to-10091
Gauche 3	HF/3-21GDOI:10042/to-10082 DFT/B3LYP/6-31G*DOI:10042/to-10083
Gauche 4	HF/3-21GDOI:10042/to-10086 DFT/B3LYP/6-31G*DOI:10042/to-10084
Gauche 5	HF/3-21GDOI:10042/to-10088 DFT/B3LYP/6-31G*DOI:10042/to-10089
Gauche 6	HF/3-21GDOI:10042/to-10084 DFT/B3LYP/6-31G*DOI:10042/to-10085

The HF/3-21g method is primitive, thus the conformers were reoptimised using the DFT B3LYP method with 6-21G* basis set.

Relative Energies: References (Gauche 3 for HF/3-21G) (Anti 1 for DFT/B3LYP/6-31G)

Conformation	Energy[HF/3-21G]/Eh	(Rel)ΔE/kcalmol-1	Energy[DFT/B3LYP/6-31G]/Eh	(Rel)ΔE/kcalmol-1
Anti 1	-231.69260	0.037	-234.61180	0.000
Anti 2	-231.69254	0.079	-234.61170	0.063
Anti 3	-231.68907	2.253	-234.60964	1.355
Anti 4	-231.69097	1.061	-234.61079	0.634
Gauche 1	-231.68772	3.103	-234.60788	2.460
Gauche 2	-231.69167	0.624	-234.61070	0.690
Gauche 3	-231.69266	0.000	-234.61133	0.295
Gauche 4	-231.69153	0.710	-234.61048	0.828
Gauche 5	-231.68962	1.911	-234.60911	1.688
Gauche 6	-231.68916	2.197	-234.60889	1.826

The results were surprising in that the HF method predicted the Gauche 3, Anti 1, and Anti 2 forms to be most stable whereas the DFT B3LYP method predicted only predicted the Anti 1 and Anti 2 formers to be most stable.

Key Notes:

Σ(E_elec + ZPE)/Eh - refers to the potential energy at 0 K including the zero-point vibrational energy.

Σ(E_elec + E_therm)/Eh - refers to the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature.

Σ(H_elec + H_therm)/Eh - contains an additional correction for RT (H = E + RT).

Σ(G_elec + G_therm)/Eh - contains the entropic contributions to the free energy (G = H - TS)

Temperature Corrections

# freq=(readisotopes) rb 3lyp/6-31g(d) geom=connectivity

The thermochemistry of anti 2 was recalculated under 0 K.

Optimising Transition States

In terms of the energy diagram the minima, i.e. the products, and the reactants (in this case as the investigation is on a rearrangement), were determined in the optimisation of the conformers of 1,5-hexadiene.

To optimise the transition states of the rearrangement, the two possible transition states were possible: chair and boat. To do this an allyl fragment (CH₂CHCH₂) was optimised and orientated in the correct positions for the two transition states and optimised to determine the guess structures for the two transition states.

Chair TS - TS(Berny) Optimisation

opt=(calcfc,ts,noeigen freq hf/3-21g geom=connectivity

The fragments on the guess structure were positioned approximately 0.220 nm apart angled at 109.5^o between the two terminal ends.

The optimisation seemed successful. There was an imaginary vibrational frequency at -817.86 cm^-1. The vibrational mode may be found here. The full optimisation may be found here DOI:10042/to-10093 .

The distance between the terminal ends had shortened to 0.202 nm.

Chair TS - Frozen Coordinate Method

opt=(calcfc,modredundant) rhf/3-21g geom=connectivity

In this method, the terminal ends were "frozen" (i.e. fixed) to 0.220 nm using the Redundant Coord Editor on GaussView and optimised. Then when the job had finished, the fragments were "unfrozen" and optimised again. ( DOI:10042/to-10167 DOI:10042/to-10168 )

The distance between the two terminal ends was 0.220 nm for the frozen structure and 0.202 nm for the unfrozen structure. The final conformations were the same indicating both methods were in agreement with each other.

Boat TS - QST2 Method

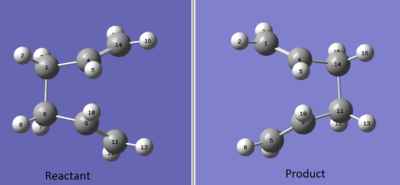
For this investigation two anti 2 conformers were taken and the atoms were labelled fully for both Reactant and Product. For the boat transition state to be located the central C-C-C-C dihedral angle was changed to 0^o, and the central C-C-C were reduced to 100^o.

After the atoms were orientated in a specific way the structures were optimised using :

opt=qst2 freq hf/3-21g geom=connectivity

There was an imaginary vibrational frequency at -840.08 cm^-1. The vibrational mode may be found here. The full optimisation may be found here DOI:10042/to-10101 .

The distance between the two terminal ends was found to be 0.214 nm, slightly further apart than the chair transition state.

Discussion

The symmetry of the transition states were C_2h (Chair TS) and C_2v (Boat TS) respectively.

Intrinsic Reaction Coordinate Analysis

To check that the optimised transition states above had optimised fully the intrinsic reaction coordinate calculations were run which uses the imaginary vibrational mode found in the frequency analysis above (showing the Cope Rearrangement reaction pathway) and determines the energy stability in steps. This gives a good indication on whether the transition state is at a maximum of an energy diagram.

Chair Analysis

# irc=(forward, maxpoints=50,calcfc) ram1 geom=connectivity

GaussView predicted the following IRC pathway.

Chair IRC Initial (Maxpoints=50)DOI:10042/to-10108

Final Conformation	Total Energy	RMS Gradient

It was fairly obvious looking at the energy diagram that although the transition state was at the maximum, no enough steps had been determined in the forward direction and that the graph did not reach an asymptote. Hence the code was changed so that the force constants would be determined at every step.

# irc=(forward, maxpoints=50,calcall) ram1 geom=connectivity

Chair IRC Edit (Maxpoints=50,calcall)

Final Conformation	Total Energy
DOI:10042/to-10159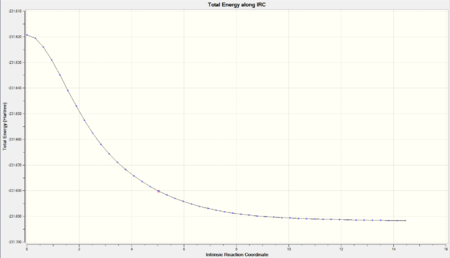

This time the energy path converged to an asymptote, which structural and energy analysis determined to be Gauche 2 (from the 1,5-hexadiene conformers).

Boat

# irc=(forward, maxpoints=50,calcfc) ram1 geom=connectivity

Boat IRC Initial (Maxpoints=50)DOI:10042/to-10100

Final Conformation	Total Energy	RMS Gradient

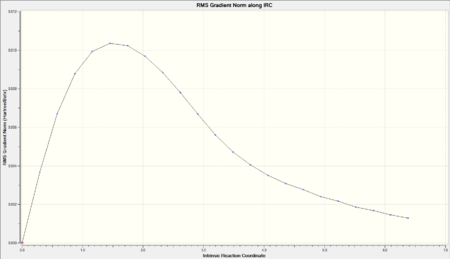A similar problem encountered for the IRC analysis of the boat transition state. Again, "calcall" was used however that proved unsuccessful. Thus the maxpoints was increased to 100.

# irc=(forward, maxpoints=100,calcall) ram1 geom=connectivity

Boat IRC Edit (Maxpoints=100)

Final Conformation	Total Energy
DOI:10042/to-10160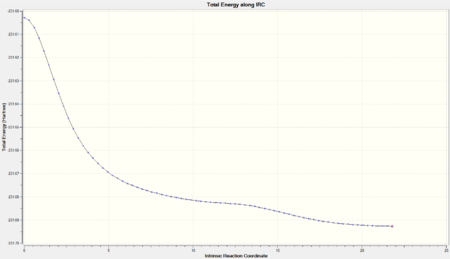

The energy path converged to an asymptote, which structural and energy analysis determined to be Gauche 3 (from the 1,5-hexadiene conformers).

Activation Energies

The activation energies were determined by taking the difference in energy, i.e. ΔE, between the energies of the transition state (the maximum) and the energies of anti 2 (the minimum). The sum of electronic and zero-point energies gave the energy difference, i.e. the activation energy, at 0 K and the sum of electronic and thermal energies gave the energy difference at 298.15 K. (The conversion of 1 Eh = 627.509 kcal/mol was used). The energy values for Anti 2 were used as suggested in the script.

Energies

	HF/3-21g: ChairDOI:10042/to-10153 and BoatDOI:10042/to-10152 TS			DFT B3LYP/6-31 G*: ChairDOI:10042/to-10158 and BoatDOI:10042/to-10157 TS
Transition State	Electronic Energy/Eh	Sum of Electronic and Zero-Point Energies/Eh	Sum of Electronic and Thermal Energies/Eh	Electronic Energy/Eh	Sum of Electronic and Zero-Point Energies/Eh	Sum of Electronic and Thermal Energies/Eh
Chair TS	-231.61932	-231.46670	-231.46134	-234.55698	-234.41493	-234.40901
Boat TS	-231.60280	-231.45093	-231.44530	-234.54309	-234.40234	-234.39601
Reactant (Anti 2)	-231.69254	-231.53954	-231.53257	-234.61170	-234.46921	-234.46186

Summary of Activation Energies /kcalmol^-1

	HF/3-21g		DFT B3LYP/6-31G*		Lit.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	44.70	34.06	33.16	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.96	41.32	44.7 ± 2.0

The values obtained for the activation energies agreed with the literature. It was believed the DFT B3LYP/6-31G* method with basis set was sufficiently accurate.

Discussion

The chair transition state converged/minimised to a Gauche 2 and the boat transition state converged to a Gauche 3. It was considered after activation energies were derived that perhaps ΔE should be calculated from the energy values obtained for Gauche 2 (for chair TS) and Gauche 3 (for boat TS) rather than Anti 2.

Activation Energies Revisited DFT B3LYP/6-31G*

Transition State	Sum of Electronic and Zero-Point Energies/Eh	Sum of Electronic and Thermal Energies/Eh
Chair TS	-234.41493	-234.40901
Reactant (Gauche 2)	-234.46821	-234.46094
Boat TS	-234.40234	-234.39601
Reactant (Gauche 3)	-234.46849	-234.46146

Thus the activation energies were 33.43 (0 K) and 32.59 (298.15 K) for the Chair TS and 41.51 (0 K) and 41.07 (298.15 K). These were not as accurate as the previous results obtained using anti 2. This was interesting as no free rotation would occur at absolute zero and thus the calculated minima (conformers) would be expected.

It was also worthwhile mentioning that the length between the terminal ends are different for HF calculations than DFT.

Distance between the allyl terminal ends /nm

Transition State	Computational Method	Distance /nm
Chair	HF	0.202
Chair	DFT	0.197
Boat	HF	0.214
Boat	DFT	0.221

The Diels-Alder Cycloaddition

Introduction

Cis-butadiene and ethylene react via a [4π_s + 2π_s] Diels-Alder Cycloaddition to produce cyclohexene. The transition states in this investigation was found using AM1 semi-empirical calculations.

Frontier Orbitals of the Fragments

HOMO/LUMO of Fragments

Cis-butadiene HOMO	Cis-butadiene LUMO
Ethylene HOMO	Ethylene LUMO

Summary of Orbital Symmetries

System	Molecular Orbital	Symmetry in the Horizontal Plane	Symmetry in the Vertical Plane
Cis butadiene HOMO		Antisymmetric	Antisymmetric
Cis butadiene LUMO		Antisymmetric	Symmetric
Ethylene HOMO		Antisymmetric	Symmetric
Ethylene LUMO		Anyisymmetric	Antisymmetric

The HOMO of ethylene and the LUMO of cis butadiene were symmetric with repect to the vertical plane of symmetry whereas the LUMO of ethylene and the HOMO of cis butadiene were antisymmetric.

Transition State Optimisation

opt=(calcfc,ts,noeigen) freq am1 geom=connectivity

The transition state was calculated.

There was an imaginary frequency at -955.59cm^-1 which showed a syn- reaction pathway. (View hereDOI:10042/to-10141 ).

Low real frequencies did not show the reaction pathway with certainty (147.12 cm^-1 showed wagging, 246.64 cm-1 showed rocking) but a vibrational mode at 272.37 cm^-1 showed certain elements of the reaction path.

The two partly formed C-C σ bonds were found to be 0.212 nm long.

A DFT level calculation was also run.

# opt=(calc,ts) freq rb31yp/6-31g(d) geom=connectivity

IRC

# irc=(forward,maxpoints=100,calcall) ram1 geom=connectivity

# irc=(reverse,maxpoints=100,calcall) ram1 geom=connectivity

Reverse/Forward maxpoints=100

Element	ReverseDOI:10042/to-10143	ForwardDOI:10042/to-10142
Product Conformation	Distance between fragments = 0.212 nm	Distance between fragments = 0.152 nm
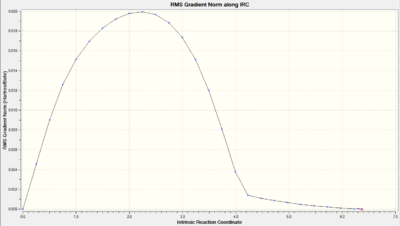
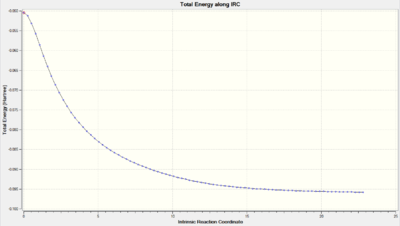
Total Energy along IRC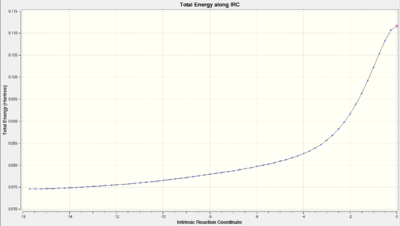
RMS Gradient along IRC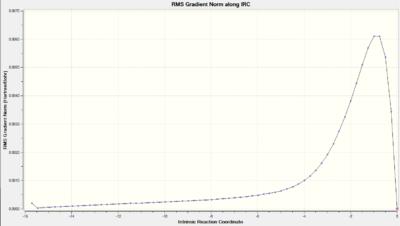

As we can observe from the Total Energy along the IRC, the transition state was indeed at the maximum on the energy graph. It was also worth noting that the shape of the energy curve suggests a fast optimisation to the transition state but quite a slow bond-making step (i.e. the process of the π orbitals of the dienophile forming two new σ bonds with the π orbitals of the diene).

MO of TS

HOMO/LUMO of TS DOI:10042/to-10141

HOMO (-0.324)	LUMO (0.023)

Summary of Orbital Symmetries

System	Molecular Orbital	Symmetry in the Horizontal Plane	Symmetry in the Vertical Plane
HOMO of TS		Antisymmetric	Antisymmetric
LUMO of TS		Antisymmetric	Symmetric

The HOMO of the transition state has been made from the HOMO of cis butadiene and the LUMO of ethylene whereas the LUMO of the transition state has been made from the LUMO of cis butadiene and the HOMO of ethylene. The information agreed with the symmetries: the HOMO of TS is antisymmetric made from two antisymmetric fragments, the LUMO of TS is symmetric made from two symmetric fragments.

The Study of the Regioselectivity of the Diels-Alder Reaction

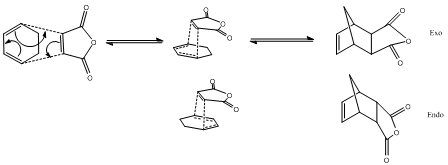
The cycloaddition of cyclohexa-1,3-diene with maleic anhydride produces two isomers, endo and exo. The primary product is the endo adduct. The reaction is supposedly under kinetic control thus the exo transition state is believed to be higher in energy.

The Optimisation of the Transition States

The optimisation was run using the AM1 method.

Frequency Data

Conformation	Imaginary Frequency (cm-1)	Vibrational Motion	Visualisation	DOI
Endo	-806.38		Visualise	DOI:10042/to-10144
Exo	-812.21		Visualise	DOI:10042/to-10145

IRC Analysis

IRC was run to check for the completion of the optimisation of the transition states.

IRC Data

Isomer	Reverse: Total Energy	Forward: Total Energy	Initial Conformation (Reverse)	Final Conformation (Forward)
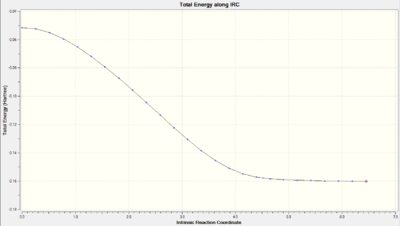
Endo	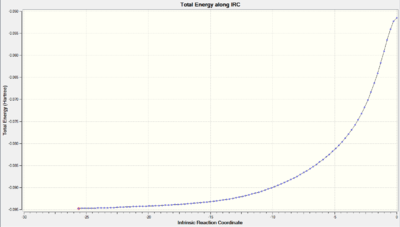DOI:10042/to-10147	DOI:10042/to-10146
Exo	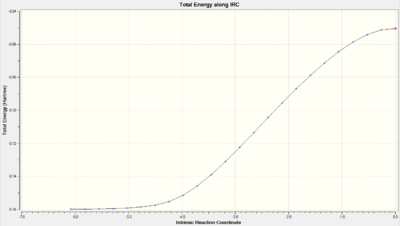DOI:10042/to-10148	DOI:10042/to-10149

The transition states were indeed at the maxima however the curves produced were interestingly not of the same shape. The IRC energy path of the exo seemed to proceed in different directions (i.e. forward for reverse and reverse for forward).

Relative Energies

The relative energies of the transition states were as follows - the end products were also observed:

Relative Energies

Isomer	Relative Energy (AM1)/Eh		Isomer End Product	Relative Energy (AM1)/Eh
Endo	-0.051505		Endo End Product (IRC Forward: Step 26)	-0.160170
Exo	-0.050420		Exo End Product (IRC Forward: Step 24)	-0.159909

The endo transition state was lower in energy (i.e. more stable) as well as the endo end product (obviously the transition state being much less stable than the end product). The end products do not differ in energy by a large amount (0.163780 kcal/mol) but the transition state relative energies differ by 0.680845 kcal/mol. This showed that the the endo form was more kinectically, and thermodynamically stable.

MO Analysis

Molecular Orbital Data

Isomer	HOMO Front	HOMO Back	LUMO Front	LUMO Back
Endo (HOMO -0.345) (LUMO -0.036 )
Exo (HOMO -0.343) (LUMO -0.040)

The HOMO and the LUMO of the two transition states looked fairly similar however there were some major differences.

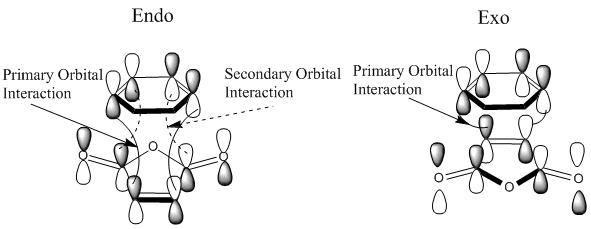
Secondary Orbital Interactions

Secondary Orbital Interactions (LUMO+2)

Isomer	Front	Side
Endo 0.029
Exo 0.034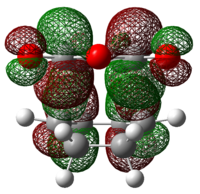

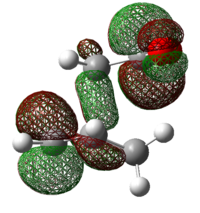
Secondary Orbital Interactions (SOI) were found in the LUMO+2 of the transition states. As seen from the diagram above, the endo transitions has SOI but not exo.