Rep:Mod:ht309mod2
3rd Year Computational Labs: Hideki Tanimura
Introduction
In this investigation quantum mechanics is be used to calculate the structure of molecules. There are many methods/algorithms written to take into account a wide range of molecular interactions, both inter- and intra-. Of course some mechanical models are more complex than other and such methods require more computational power and time. This is why the DFT (Density Functional Theory) calculations using the B3LYP method was used to compute all of the molecules in this investigation as this is excellent for predicting molecular structures to high accuracy while requiring little computational processing[1].
Analysis of BH3
Optimisation of BH3
BH3 was optimised on Gaussian using the (Density Function Theory) DFT/B3LYP method with a STO 3-21g basis set. The bond B-H was originally set to 1.5Å. The summary file looked like thus:
BH3 optimisation File Name = BH3_opt File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 3-21G Charge = 0 Spin = Singlet E(RB3LYP) = -26.46226338 a.u. RMS Gradient Norm = 0.00020672 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 0 minutes 19.0 seconds.
The RMS gradient was 0.00020672 a.u. which was less than 0.001> and thus the optimisation was thought to be successful and complete. This is due to the fact the optimsed form should lie on the stationary point of the Energy graph (i.e. located at the minimum of the 1st derivative). The convergence of the job was also checked.
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1935 -DE/DX = 0.0004 !
! R2 R(1,3) 1.1935 -DE/DX = 0.0004 !
! R3 R(1,4) 1.1935 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad

The data showed that the bond lengths (B-H) were all 1.1935Å (Lit.[2] 1.19Å) and the bond angles (H-B-H) were all 120o suggesting the molecule was trigonal planar (i.e. a point group of D3h (). The primitive STO 3-21g basis set was good enough for the optimisation of BH3 as the molecule is very simple and highly symmetric (Dh3).
To check that the optimisation was complete and correct the output values were annalysed:
We can observe from the two graphs that the structure was optimised using 4 steps. Both total energy and RMS gradient tend to an assymptote. For the total energy, the assymptote lies around -26.4 a.u. which was the value determined by the optimisation calculation earlier. The assymptote for the RMS gradient lies around 0. Optimisation step 4 is fairly close to this line suggesting that the optimisation was complete (i.e. -dV/dx=0, the minimum, or the potential well).
Vibrational Analysis of BH3
The completion of the optimisation was checked by analysing the vibrational frequencies of BH3. The calculations were done using the 3-21G basis set.
| Number | Form of the Vibration | Frequency | Intensity | Symmetry D3h Point Group | Animation |
|---|---|---|---|---|---|
| 1 | Wagging (umbrella motion) | 1144.15 | 92.9 | A2" | |
| 2 | In-plane Scissoring (Bending motion) | 1203.64 | 12.3 | E' | |
| 3 | Rocking (Bending motion) | 1203.64 | 12.3 | E' | |
| 4 | Symmetrical Stretching | 2598.42 | n/a | A1' | |
| 5 | Asymmetrical Stretching | 2737.44 | 103.7 | E' | |
| 6 | Asymmetrical Stretching | 2737.44 | 103.7 | E' |
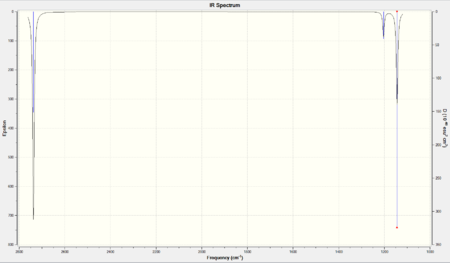
There were six vibrational modes. The positive values of the frequencies suggested complete optimisation of the molecule on Gaussian as a negative frequency would have been an indication of the structure being in the transition state; i.e. not in the ground state.
There were six vibrational modes however only 3 peaks were present on the IR spectrum. The reason for this was that the symmetrical stretching mode (mode 4) does has a net dipole moment of 0. This was why the intensity of the peak was 0 due to its IR inactivity (only molecular vibrations with which involve changes in dipole moments are IR active). Modes 2 and 3 (1204cm-1), and 5 and 6(2737cm-1), were degenerate. This meant the peaks were superimposed as pairs.
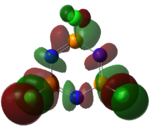
Molecular Orbital Analysis of BH3
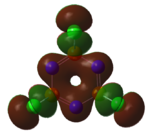
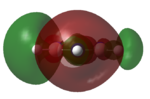
Using Gaussian the following MO diagram was constructed.
Gaussian managed to predict the two pairs of degenerate orbitals 1e' and 2e' correctly. The energies provided with the relevant molecular orbitals seemed to show the energy splitting. Gaussian calculated that 3a1' was higher in energy than 2e'. The ordering for these is relatively difficult as a1' energy levels are lower than e' but s-s interactions are stronger than s-p. A small error in the energy of the degenerate energy levels were expected however there were no discrepancies in the energy values. An explanation for this could have been the highly symmetrical of this very simple molecule.
NBO Analysis of BH3
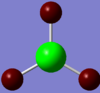
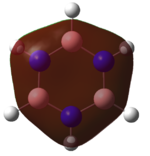
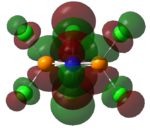
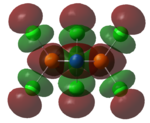
The charge distribution on BH3 was calculated using DFT/B3LYP with the STO 3-21g basis set. To the right is the representation of the charge distribution. The Boron atom is green as it has a positive charge of 0.33161, and the hydrogen atoms are red as they have a negative charge of -0.11054 each. The net charge here is 0 as the molecule is completely symmetrical.
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.33161 1.99903 2.66935 0.00000 4.66839
H 2 -0.11054 0.00000 1.11021 0.00032 1.11054
H 3 -0.11054 0.00000 1.11021 0.00032 1.11054
H 4 -0.11054 0.00000 1.11021 0.00032 1.11054
=======================================================================
* Total * 0.00000 1.99903 6.00000 0.00097 8.00000
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99853) BD ( 1) B 1 - H 2
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 2 s(100.00%)
1.0000 0.0000
2. (1.99853) BD ( 1) B 1 - H 3
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 3 s(100.00%)
1.0000 0.0000
3. (1.99853) BD ( 1) B 1 - H 4
( 44.48%) 0.6669* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.52%) 0.7451* H 4 s(100.00%)
1.0000 0.0000
4. (1.99903) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
The data above showed that the molecule was sp2 hybridised. This was correct as the molecule is trigonal planar. The lone pair was labelled as having 100% s-character although theoretically it is the empty p orbital orthogonal to the plane.
Analysis of TlBr3
Optimisation of TlBr3
TlBr3 was optimised using the DFT/B3LYP method using the LANL2DZ basis set. The conformation was constrained to D3h to save calculation time as TlBr3 due to the molecule containing many (186 = 81(Tl) + 3 x 35(Br)) electrons. With such large atoms involved a pseudo-potential had to be used as both atoms exhibit relativistic effects which cannot be recovered by the standard Schrödinger wave equation. The optimisation calculated the bond angle of 120o (which it was originally constraint to) and the bond length of 0.265 nm (lit.[3] 0.265 nm).
TlBr3 optimisation File Name = tlbr3_optimisation File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -91.21812851 a.u. RMS Gradient Norm = 0.00000090 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 0 minutes 29.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.083881D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.651 -DE/DX = 0.0 !
! R2 R(1,3) 2.651 -DE/DX = 0.0 !
! R3 R(1,4) 2.651 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
All parameters had converged fully and thus optimisation was complete.
Frequency Analysis of TlBr3
The following data were obtained using Gaussian.
tlbr3_hidekitanimura_freq File Name = tlbr3_freq File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -91.21812851 a.u. RMS Gradient Norm = 0.00000088 a.u. Imaginary Freq = 0 Dipole Moment = 0.0000 Debye Point Group = D3H Job cpu time: 0 days 0 hours 0 minutes 28.0 seconds.
| Number | Form of the Vibration | Frequency | Intensity | Symmetry D3h Point Group | Animation |
|---|---|---|---|---|---|
| 1 | Wagging (Umbrella motion) | 46.43 | 3.7 | E' | |
| 2 | In-plane Scissoring (Bending motion) | 46.43 | 3.7 | E' | |
| 3 | Rocking (Bending motion) | 52.14 | 5.8 | A2" | |
| 4 | Symmetrical Stretching | 165.27 | n/a | A1' | |
| 5 | Asymmetrical Stretching | 210.69 | 25.5 | E' | |
| 6 | Asymmetrical Stretching | 210.69 | 25.5 | E' |
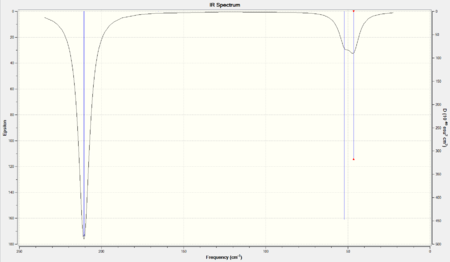
The vibrational frequencies calculation produced the vibrational modes to BH3. This was expected as both molecules are D3h. A similar explanation used for the BH3 to explain the IR spectrum may be repeated here.
The major difference between the spectra for BH3 and TlBr3 was that the frequencies of the vibrational modes obtained for TlBr3 were substantially lower than those obtained for BH3. This was believed to be due to the mass of the atoms involved; since the mass of the atoms were considerably larger than the boron - hydrogen model that the maximum displacement of the oscillation (or the stretch) was higher (since mass and amplitude are directly proportional in a harmonic oscillator). A higher amplitude results in a lower frequency naturally.
Below are the "Low frequencies" found in the .log file.
Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367
The lowerst "real" normal mode was at 46.43 cm-1.
What is a Bond?
A bond is an inter-atomic attraction caused by electromagnetic forces. It is the net result of attractions and repulsions between opposite charges (i.e. the electrons and the nuclei) of the two atoms involved in the bond. The attractive force is proportional to the length of the bond, or the length between the two atoms, but is not constant as the two atoms interact in the way harmonic oscillators do. This results in the shortening, and lengthening of the bond (or the stretching) and the definitive "bond length" is situated at the equilibrium where the potential well is situated.
Analysis of Isomers of Mo(CO)4L2 - Cis Trans Isomerism
Optimisation
The structures were initially calculated using the DFT/B3LYP method with the LANL2MB basis set with the additional keyword of opt=loose to allow for a fast calculation of the rough structures.
cis mo optimisation File Name = cis_mo_opt File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2MB Charge = 0 Spin = Singlet E(RB3LYP) = -617.52474543 a.u. RMS Gradient Norm = 0.00012927 a.u. Imaginary Freq = Dipole Moment = 8.8270 Debye Point Group = C1 Job cpu time: 0 days 0 hours 11 minutes 34.8 seconds.
transmo optimisation File Name = Mo trans opt File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2MB Charge = 0 Spin = Singlet E(RB3LYP) = -617.52205032 a.u. RMS Gradient Norm = 0.00013831 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = C1 Job cpu time: 0 days 0 hours 5 minutes 56.0 seconds.

The cis isomer was found to be more stable than the trans. The dipole moments for the two isomers were 8.83D (surprisingly large) and 0D (expected due to symmetry). Then the optimised geometries were manually altered (see right) and re-optimised using the LANL2DZ basis set with the additional keywords in=ultrafine sc=conver=9.
cis mo optimisation File Name = cismodz File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -623.57707196 a.u. RMS Gradient Norm = 0.00000333 a.u. Imaginary Freq = Dipole Moment = 1.3101 Debye Point Group = C1 Job cpu time: 0 days 1 hours 5 minutes 9.8 seconds.
transmo optimisation File Name = trans_opt_corr File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = LANL2DZ Charge = 0 Spin = Singlet E(RB3LYP) = -623.57603106 a.u. RMS Gradient Norm = 0.00002235 a.u. Imaginary Freq = Dipole Moment = 0.3010 Debye Point Group = C1 Job cpu time: 0 days 1 hours 2 minutes 4.4 seconds.
The second optimisation agained calculated the cis as the more stable isomer. The dipole moments were now 1.31D (cis) and 0.30D (trans) respectively. The dipole moment in the trans isomer was due to the manual alterations to the molecule; i.e. the loss of centre of inversion, and thus symmetry. (The .log files can be found here cis:DOI:10042/to-9691 , trans:DOI:10042/to-9692 ). The difference in energy was -623.57603106 + 623.57707196 = 0.0010409 Ha. This converts to 2.73 kJmol-1 (a small energy gap). Literature[4] reports that the trans isomer is more stable than cis and that the cis isomerises to the trans in room temperature. This contradiction may be explained by the fact PPh3 was substituted by PCl3.
Bond Lengths and Angles
The structures were investigated further by comparing bond lengths and bond angles.
| Bond | Length |
|---|---|
| P - Mo | 0.253 |
| C - Mo | 0.211 |
| P - Cl | 0.240 |
| C - O | 0.119 |
| Bond | Length |
|---|---|
| P - Mo | 0.244 |
| C - Mo | 0.206 |
| P - Cl | 0.224 |
| C - O | 0.117 |
Generally bond lengths were longer in the cis isomer hence the extra stability minimising steric repulsion.
The bond angles of P-Mo-P of cis and trans were (94.1o and 177.4o respectively). The cis isomer showed that there was definite steric repulsion between the two large PCl3 ligands. The trans isomer showed that the structure was not perfectly symmetrical.
Frequency
| Cis-Isomer | Trans-Isomer |
|---|---|
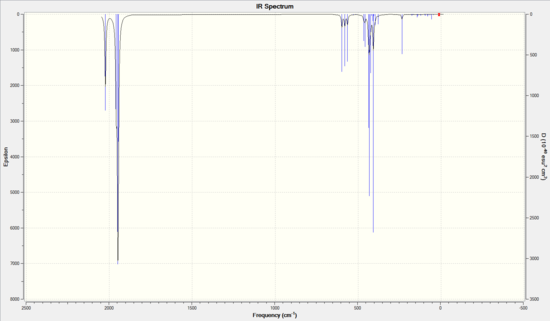 |
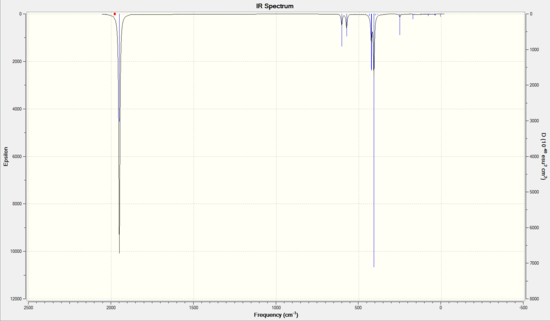
|
The main difference in the IR spectra of the two isomers was found to be in the carbonyl stretching region.

| Mode | Frequency | Intensity | 3D |
|---|---|---|---|
| 42 | 1945.31 | 762.9 | |
| 43 | 1948.67 | 1498.4 | |
| 44 | 1958.36 | 632.8 | |
| 45 | 2023.32 | 597.8 |

| Mode | Frequency | Intensity | 3D |
|---|---|---|---|
| 42 | 1950.31 | 1475.5 | |
| 43 | 1950.91 | 1466.7 | |
| 44 | 1977.19 | 0.5 | |
| 45 | 2030.98 | 3.7 |
There were four vibrational modes in the carbonyl region. The cis isomer showed two peaks and the trans showed one. The cis isomer had three overlapping peaks around 1950 cm-1, with the other at 2023 cm-1. The trans had two superimposed peaks at 1950 cm-1. The other peaks were of too low an intensity to be visible on the spectrum.
Mini Project
Introduction
The investigation concentrated on three aromatic ring structures benzene, borazine, and phosphazene. Using GaussView, their optimised structures, MOs and vibrations were analysed.
Optimisation Analysis
The following optimisations were calculated using the DFT/B3LYP method with the 6-311G(d,p) basis set. (Benzene: DOI:10042/to-9717 , Borazine: DOI:10042/to-9718 , Phosphazene: DOI:10042/to-9737 )
benzene_optimisation File Name = log_47675 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-311G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -232.30854378 a.u. RMS Gradient Norm = 0.00002493 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = C1 Job cpu time: 0 days 0 hours 7 minutes 21.9 seconds.
borazine_opt File Name = log_47676-1 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-311G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -242.74449029 a.u. RMS Gradient Norm = 0.00010442 a.u. Imaginary Freq = Dipole Moment = 0.0047 Debye Point Group = C1 Job cpu time: 0 days 0 hours 19 minutes 32.7 seconds.
phosphazene_opt File Name = log_47681-1 File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-311G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -3949.90748627 a.u. RMS Gradient Norm = 0.00006746 a.u. Imaginary Freq = Dipole Moment = 0.0049 Debye Point Group = C1 Job cpu time: 0 days 3 hours 42 minutes 3.1 seconds.
| Benzene | Borazine | Phosphazene |
|---|---|---|
|
|
The structures calculated by Gaussian were all planar (with the Cl-P-Cl line orthogonal to the plane of the ring in phosphazene). The dipole moments should have been all 0. The point groups should have been D6h (Benzene), D3h (Borazine), and D3h (Phosphazene). Interestingly the phosphazene proved to be the most stable molecule out of the three by far. Borazine was more stable than benzene.
Bond Lengths and Angles

| Molecule (Bond) | Bond Length/nm |
|---|---|
| Benzene (C=C) | 0.139 |
| Benzene (C-C) | 0.139 |
| Benzene (C-H) | 0.108 |
| Borazine (B-N) | 0.143 |
| Borazine (B-H) | 0.119 |
| Borazine (N-H) | 0.101 |
| Phosphazene (P-N) | 0.159 |
| Phosphazene (P-Cl) | 0.204 |
| Molecule (Angle) | Bond Angle/o |
|---|---|
| Benzene (C=C-C) | 120.0 |
| Benzene (H-C-C) | 120.0 |
| Borazine (N-B-N) | 117.1 |
| Borazine (B-N-B) | 122.9 |
| Borazine (H-N-B) | 118.5 |
| Borazine (H-B-N) | 121.5 |
| Phosphazene (N-P=N) | 116.9 |
| Phosphazene (P=N-P) | 123.1 |
| Phosphazene (Cl-P-Cl) | 102.3 |
Other than benzene the structures were not perfect rings. Both borazine and phosphazene did not have a constant bond angle of 120o inside the ring. This was due to the size of the atoms; there was more steric repulsion between larger atoms which increased the angle between them (i.e.B-N-B and P-N=P). In all structures the bond lengths between neighbouring atoms on the rings were the same.
The "diameter" of the rings were 0.279 nm (between oppposite carbons on the benzene ring), 0.286 nm (between opposite nitrogen and boron on the borazine ring), and 0.319 nm (between opposite nitrogen and phosphorus on the phosphazene ring).
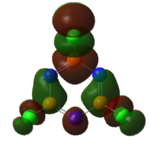
Molecular Orbital Analysis
The following MOs were calculated using DFT/B3LYP with the STO 6-311 d,p basis set (BenzeneDOI:10042/to-9740 , Borazine DOI:10042/to-9739 , Phosphazene DOI:10042/to-9738 ).
| Molecular Orbital | Benzene | Borazine | Phosphazene |
|---|---|---|---|
| LUMO+2 |  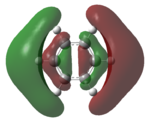 |
  |
 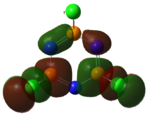
|
| LUMO+1 | 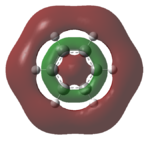 |
 |
|
| LUMO | 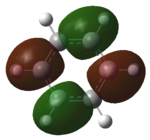  |
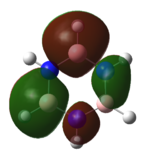  |
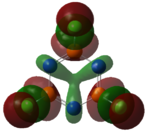
|
| HOMO |  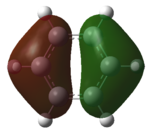 |
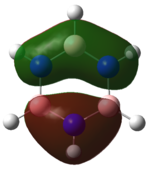 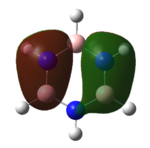 |
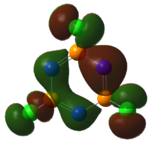 
|
| HOMO-1 | 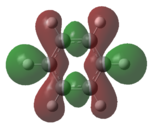 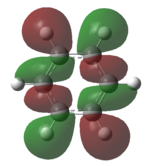 |
 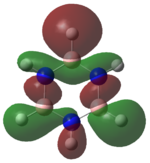 |
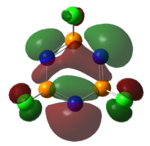 
|
| HOMO-2 |  |
 |
|
| Molecular Orbital | Benzene | Borazine | Phosphazene |
|---|---|---|---|
| LUMO+2 |   |
  |
|
| LUMO+1 |  |
 |
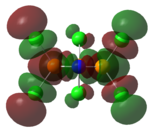 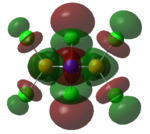
|
| LUMO | 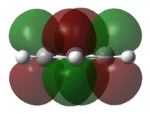 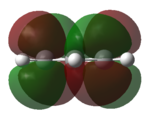 |
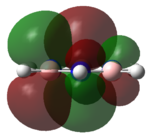 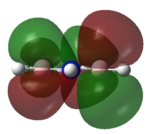 |
|
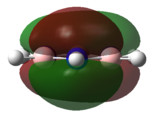
| HOMO | 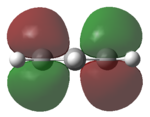 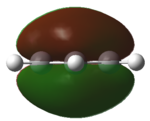 |
  |
|
| HOMO-1 | 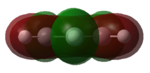 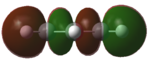 |
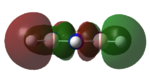 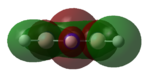 |
|
| HOMO-2 | 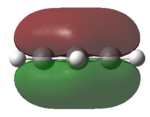 |
 |

|
| Benzene | Borazine | Phosphazene |
|---|---|---|
 |
 |

|
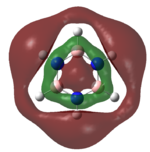
The MOs of the region between LUMO+2 and HOMO-2 were analysed.
Analysis of Benzene and Borazine MOs
The two MOs were very similar in structure and degeneracy. The values of the energy levels were very similar too. The benzene HOMO lay at -0.25637 kJmol-1 and the borazine one at -0.28513 kJmol-1. This was interesting as the LUMO for benzene was at -0.00943 kJmol-1 which was still a negative value but the borazine LUMO was at 0.01164 kJmol-1 and thus positive. The HOMO-LUMO energy gap was 0.24694 kJmol-1(benzene) and 0.29677 kJmol-1 (borazine).

Analysing the shapes of the actual MOs for HOMO and LUMO, both MOs were symmetrical, however the borazine MO was more complex. The benzene MO contained two lines of symmetry, whereas the borazine MO contained only one. This was thought to be the main source of the discrepancy between the two MO structures. The unbalance between the boron and nitrogen atoms created an overall uneven symmetry when observing the MOs from birdseye view (i.e. above and below the plane of the ring). Perhaps the main cause of this was due to the incomplete symmetry (D3h) of the optimised borazine however the symmetry of the MOs are of triangular nature compared to the ones for benzene. This triangular nature was observed easily when considering LUMO+1. The benzene MO had three delocalised rings of circular (hexagonal) nature whereas the borazine MO had three delocalised rings of triangular nature. Again, with LUMO+2, this was observed.
The π orbital energy diagram of both are as follows:
It could be concluded that borazine is less aromatic than benzene due to the unequal distribution of the p electron density. This difference in property may be demonstrated by the fact the borazine undergoes addition reactions where electrobegative substituents attack the boron and electropositive substituents attack the nitrogen. This also explains the large HOMO-LUMO energy gap.
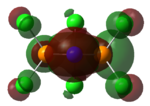
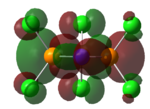
Analysis of Phosphazene
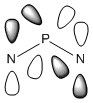
Phosphazene was somewhat harder to analyse. This was due to the fact benzene and borazine have pπ-pπ bonding but phosphazene has pπ-dπ bonding. The hybridisation at the nitrogen atom is sp2 hybridised and at the phosphorus atom is sp3 hybrised. This allows for a σ-bonded framework: The non-bonding/overlapping sp2 orbital is thus occupied a lone pair, and the pz orbital is available for further π-interaction with dxy and dyz orbitals on the phosphorus.
In terms of the molecular orbitals phosphazene was similar to borazine; the uneven distribution of p electron density is the factor again.
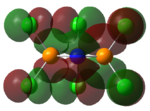
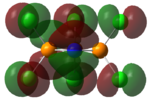
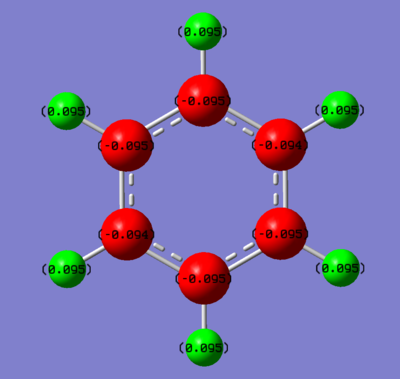
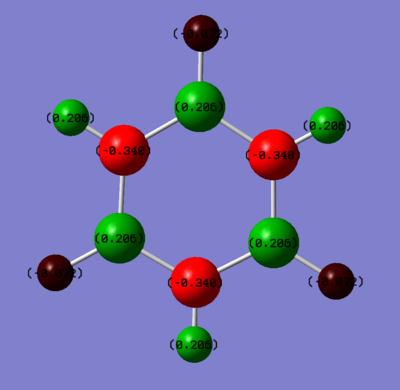
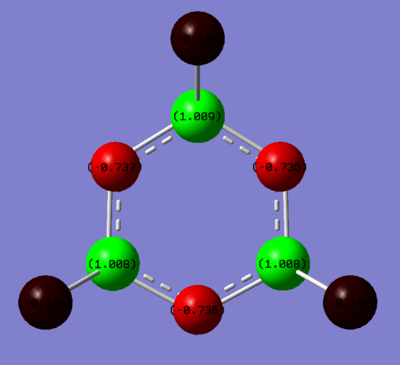
Charge Distribution/NBO
| Benzene | Borazine | Phosphazene |
|---|---|---|
 |
 |
|
Benzene
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
C 1 -0.19959 1.99911 4.18479 0.01569 6.19959
C 2 -0.19960 1.99911 4.18480 0.01569 6.19960
C 3 -0.19957 1.99911 4.18477 0.01569 6.19957
C 4 -0.19959 1.99911 4.18479 0.01569 6.19959
C 5 -0.19960 1.99911 4.18480 0.01569 6.19960
C 6 -0.19957 1.99911 4.18477 0.01569 6.19957
H 7 0.19959 0.00000 0.79790 0.00250 0.80041
H 8 0.19959 0.00000 0.79790 0.00250 0.80041
H 9 0.19959 0.00000 0.79791 0.00251 0.80041
H 10 0.19959 0.00000 0.79790 0.00250 0.80041
H 11 0.19959 0.00000 0.79790 0.00250 0.80041
H 12 0.19959 0.00000 0.79791 0.00251 0.80041
=======================================================================
* Total * 0.00000 11.99465 29.89616 0.10919 42.00000
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.97919) BD ( 1) C 1 - C 2
( 50.00%) 0.7071* C 1 s( 36.09%)p 1.77( 63.87%)d 0.00( 0.04%)
0.0001 0.6006 0.0127 0.0003 -0.6372
0.0363 -0.0008 -0.4804 -0.0225 -0.0003
0.0000 0.0000 0.0000 0.0177 0.0000
0.0000 0.0011 -0.0114
( 50.00%) 0.7071* C 2 s( 36.09%)p 1.77( 63.87%)d 0.00( 0.04%)
0.0001 0.6006 0.0127 0.0003 0.5977
0.0148 0.0005 0.5287 -0.0400 0.0007
0.0000 0.0000 0.0000 0.0167 0.0000
0.0000 0.0059 -0.0114
12. (1.97964) BD ( 1) C 4 - H 10
( 60.12%) 0.7754* C 4 s( 27.79%)p 2.60( 72.16%)d 0.00( 0.05%)
0.0004 -0.5267 0.0226 0.0006 -0.1365
-0.0025 0.0008 0.8383 0.0153 -0.0049
0.0000 0.0000 0.0000 0.0060 0.0000
0.0000 0.0179 0.0122
( 39.88%) 0.6315* H 10 s( 99.95%)p 0.00( 0.05%)
-0.9998 -0.0004 -0.0011 0.0035 -0.0215
0.0000
16. (1.99911) CR ( 1) C 1 s(100.00%)p 0.00( 0.00%)
1.0000 0.0001 0.0000 0.0000 -0.0001
0.0000 0.0000 0.0004 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000
The carbon atoms showed sp2 hybridised character (consider 1: s(36.09%), p(63.87%) - the p character is nearly double the s character.
Borazine
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
N 1 -1.04509 1.99934 6.04038 0.00537 8.04509
H 2 0.39529 0.00000 0.60186 0.00286 0.60471
N 3 -1.04507 1.99934 6.04036 0.00537 8.04507
H 4 0.39527 0.00000 0.60187 0.00286 0.60473
N 5 -1.04509 1.99934 6.04037 0.00537 8.04509
H 6 0.39528 0.00000 0.60186 0.00286 0.60472
B 7 0.73980 1.99919 2.24368 0.01733 4.26020
H 8 -0.08998 0.00000 1.08861 0.00137 1.08998
B 9 0.73979 1.99919 2.24369 0.01733 4.26021
H 10 -0.08998 0.00000 1.08861 0.00137 1.08998
B 11 0.73977 1.99919 2.24371 0.01734 4.26023
H 12 -0.08997 0.00000 1.08861 0.00137 1.08997
=======================================================================
* Total * 0.00000 11.99558 29.92361 0.08080 42.00000
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98561) BD ( 1) N 1 - H 2
( 70.14%) 0.8375* N 1 s( 22.09%)p 3.53( 77.87%)d 0.00( 0.05%)
-0.0003 0.4698 0.0127 0.0001 0.8780
0.0097 0.0006 0.0876 0.0010 0.0001
0.0007 0.0000 0.0000 0.0035 0.0001
0.0000 0.0174 -0.0119
( 29.86%) 0.5465* H 2 s( 99.94%)p 0.00( 0.06%)
0.9997 0.0024 0.0029 -0.0250 -0.0025
0.0000
2. (1.98546) BD ( 1) N 1 - B 7
( 75.74%) 0.8703* N 1 s( 38.90%)p 1.57( 61.07%)d 0.00( 0.03%)
0.0001 -0.6237 0.0045 0.0000 0.2604
-0.0200 0.0000 0.7365 0.0016 0.0000
0.0001 0.0000 0.0000 -0.0095 0.0000
0.0000 0.0091 0.0117
( 24.26%) 0.4926* B 7 s( 31.72%)p 2.15( 68.15%)d 0.00( 0.14%)
0.0001 -0.5623 -0.0310 -0.0011 -0.3227
-0.0514 -0.0053 -0.7571 -0.0355 0.0126
0.0005 0.0000 0.0000 -0.0186 0.0000
0.0000 0.0214 0.0236
13. (1.98376) BD ( 1) B 7 - H 8
( 45.23%) 0.6726* B 7 s( 36.64%)p 1.73( 63.32%)d 0.00( 0.04%)
-0.0007 0.6047 -0.0281 -0.0001 0.4639
-0.0184 -0.0003 -0.6458 0.0256 0.0004
0.0004 0.0000 0.0000 -0.0145 0.0000
0.0000 -0.0049 -0.0110
( 54.77%) 0.7400* H 8 s( 99.92%)p 0.00( 0.08%)
0.9996 0.0002 -0.0001 -0.0164 0.0228
0.0000
Again, both the boron and nitrogen atoms showed sp2 hybridised characteristics (2: B(s(38.90%), p(61.07%)), N(s(31.72%),p(68.15%))).
Phosphazene
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
N 1 -1.40641 1.99925 6.39131 0.01586 8.40641
N 2 -1.40655 1.99925 6.39144 0.01586 8.40655
N 3 -1.40658 1.99924 6.39148 0.01586 8.40658
Cl 4 -0.19481 9.99972 7.18161 0.01348 17.19481
Cl 5 -0.19453 9.99972 7.18131 0.01349 17.19453
Cl 6 -0.19476 9.99972 7.18156 0.01348 17.19476
Cl 7 -0.19473 9.99972 7.18152 0.01348 17.19473
Cl 8 -0.19473 9.99972 7.18152 0.01349 17.19473
Cl 9 -0.19456 9.99972 7.18134 0.01350 17.19456
P 10 1.79598 9.99722 3.06224 0.14456 13.20402
P 11 1.79586 9.99722 3.06241 0.14450 13.20414
P 12 1.79583 9.99722 3.06236 0.14460 13.20417
=======================================================================
* Total * 0.00000 95.98775 71.45009 0.56216 168.00000
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.97622) BD ( 1) N 1 - P 11
( 70.41%) 0.8391* N 1 s( 35.59%)p 1.81( 64.35%)d 0.00( 0.05%)
-0.0005 0.5966 -0.0058 -0.0004 -0.5849
-0.0114 -0.0056 0.5488 -0.0014 0.0002
-0.0002 0.0000 0.0000 -0.0165 0.0000
0.0000 -0.0104 -0.0129
( 29.59%) 0.5440* P 11 s( 29.74%)p 2.31( 68.77%)d 0.05( 1.49%)
0.0000 0.0001 0.5452 0.0139 -0.0015
0.0001 0.0002 0.6108 0.0061 0.0092
-0.0029 -0.0003 -0.5588 -0.0457 -0.0138
0.0028 0.0000 0.0007 0.0000 0.0000
0.0000 -0.1069 0.0002 -0.0001 0.0171
-0.0563
2. (1.81616) BD ( 2) N 1 - P 11
( 92.46%) 0.9616* N 1 s( 0.00%)p 1.00( 99.90%)d 0.00( 0.10%)
0.0000 0.0000 0.0000 0.0000 0.0002
0.0000 0.0000 0.0006 0.0000 0.0000
0.9995 -0.0015 -0.0038 0.0000 0.0071
0.0303 0.0000 -0.0001
( 7.54%) 0.2746* P 11 s( 0.00%)p 1.00( 58.61%)d 0.71( 41.39%)
0.0000 0.0000 -0.0001 -0.0001 0.0000
0.0000 0.0000 -0.0002 0.0000 0.0000
0.0000 0.0000 0.0008 0.0000 0.0001
0.0000 0.0014 0.7450 -0.0919 0.1502
0.0027 0.0006 0.6086 -0.2085 0.0001
0.0004
16. (1.99924) CR ( 1) N 1 s(100.00%)p 0.00( 0.00%)
1.0000 0.0002 0.0000 0.0000 0.0003
0.0000 0.0000 0.0010 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000
49. (2.00000) CR ( 1) P 10 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000
64. (1.83952) LP ( 1) N 1 s( 28.83%)p 2.47( 71.09%)d 0.00( 0.08%)
0.0007 0.5366 0.0184 0.0005 -0.2175
0.0009 0.0006 -0.8146 0.0032 0.0021
0.0005 0.0000 0.0000 -0.0133 0.0000
0.0000 0.0231 0.0110
The phosphazene hybridisation was different. The nitrogen atom showed sp2 hybridised characteristics (1: s(35.59%),p(64.35%)) as well as the phosphorus (1: s(29.74%), p(68.77%)) however they both showed different characteristics as well. The nitrogen sometimes has a p orbital (2: p(99.9%)) and the phosphorus has a p-d orbital (2: p(58.61%),d(41.39%)). As explained in the MO analysis section, P-N bonding is slightly more complex than C-C or B-N as phosphorus has d orbitals. The nitrogen has a lone pair which has sp3 hybridised characteristics - this is the non-bonding pz orbital.
Vibrational Frequencies
The major peaks on the IR were analysed. To analyse them fully, the symmetries were constrained to D6h (benzeneDOI:10042/to-9942 ), and D3h (borazineDOI:10042/to-9946 , phosphazeneDOI:10042/to-9947 ) - the symmetrical stretche (i.e. IR inactive) peaks were ignored.
Benzene
Low frequencies --- -0.0096 -0.0047 -0.0047 10.0410 10.0410 14.0914
Low frequencies --- 412.4836 412.4836 623.3059
1 2 3
E2U E2U E2G
Frequencies -- 412.4836 412.4836 623.3059
4 5 6
E2G A2U B2G
Frequencies -- 623.3059 687.1341 722.9800
7 8 9
E1G E1G E2U
Frequencies -- 861.1923 861.1923 980.3667
10 11 12
E2U A1G B2G
Frequencies -- 980.3667 1013.0127 1015.4615
13 14 15
B1U E1U E1U
Frequencies -- 1023.4434 1060.3396 1060.3396
16 17 18
B2U E2G E2G
Frequencies -- 1174.6557 1197.5691 1197.5691
19 20 21
B2U A2G E1U
Frequencies -- 1334.6342 1381.9262 1513.0041
22 23 24
E1U E2G E2G
Frequencies -- 1513.0041 1637.1672 1637.1672
25 26 27
B1U E2G E2G
Frequencies -- 3155.5713 3165.1992 3165.1992
28 29 30
E1U E1U A1G
Frequencies -- 3180.9870 3180.9870 3191.5956
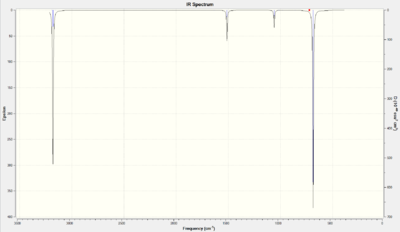
| Number | Form of the Vibration | Frequency | Intensity | Animation | Symmetry Point Group |
|---|---|---|---|---|---|
| 5 | Wagging (Umbrella motion) | 687.1 | 110.7 | E2g | |
| 14 | In-plane Scissoring (Bending motion) | 1060.3 | 5.2 | B1u | |
| 15 | In-plane Scissoring (Bending motion) | 1060.3 | 5.2 | E1u | |
| 21 | In-plane Scissoring (Bending motion) | 1513.0 | 8.9 | E1u | |
| 22 | In-plane Scissoring (Bending motion) | 1513.0 | 8.9 | E1u | |
| 28 | Asymmetrical Stretching | 3181.0 | 44.2 | E1u | |
| 29 | Asymmetrical Stretching | 3181.0 | 44.2 | E1u |
There were four distinct peaks on the benzene IR spectrum: these were 3 pairs of degenerate energy levels (14&15, 21&22, 28&29) and one very intense peak for wagging at 687.1 cm-1. There were 30 vibrational modes due to 3 x 12 - 6 = 30.
Borazine
Low frequencies --- -18.8372 -18.7399 -16.5390 -0.0105 0.0177 0.0564
Low frequencies --- 289.5569 289.5613 408.6377
1 2 3
E" E" A2"
Frequencies -- 289.5562 289.5605 408.6377
4 5 6
E' E' E"
Frequencies -- 528.1088 528.1113 715.8125
7 8 9
E" A2" A1'
Frequencies -- 715.8146 729.4025 864.4246
10 11 12
E" E" A2"
Frequencies -- 924.2432 924.2449 936.0837
13 14 15
E' E' A1'
Frequencies -- 939.4777 939.4825 946.3617
16 17 18
A2' E' E'
Frequencies -- 1046.6737 1080.8339 1080.8366
19 20 21
A2' A2' E'
Frequencies -- 1228.2135 1324.4562 1398.1837
22 23 24
E' E' E'
Frequencies -- 1398.1951 1485.1877 1485.1881
25 26 27
E' E' A1'
Frequencies -- 2609.1170 2609.1187 2619.3182
28 29 30
A1' E' E'
Frequencies -- 3627.9598 3629.8417 3629.8417
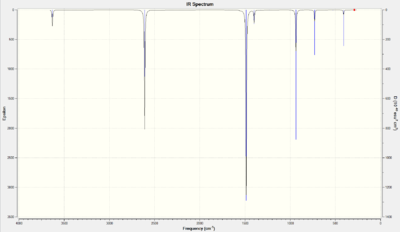
| Number | Form of the Vibration | Frequency | Intensity | Animation | Symmetry Point Group |
|---|---|---|---|---|---|
| 3 | Wagging (Umbrella motion) | 408.6 | 24.9 | A2" | |
| 4 | In-plane Twisting | 528.1 | 0.5 | E' | |
| 5 | In-plane Scissoring (Bending motion) | 528.1 | 0.5 | E' | |
| 8 | Wagging (Umbrella motion) | 729.4 | 55.5 | A2" | |
| 12 | Wagging | 936.1 | 205.6 | A2" | |
| 13 | In-plane Scissoring (Bending motion) | 939.5 | 0.1 | E' | |
| 14 | In-plane Scissoring (Bending motion) | 939.5 | 0.1 | E' | |
| 17 | Wagging (umbrella motion) | 1080.8 | 0.0 | E' | |
| 18 | In-plane Scissoring (Bending motion) | 1080.8 | 0.0 | E' | |
| 21 | In-plane Scissoring (Bending motion) | 1398.2 | 33.3 | E' | |
| 22 | In-plane Scissoring (Bending motion) | 1398.2 | 33.3 | E' | |
| 23 | Asymmetrical Stretching | 1485.2 | 479.6 | E' | |
| 24 | Asymmetrical Stretching | 1485.2 | 479.6 | E' | |
| 25 | Asymmetrical Stretching | 2609.1 | 295.3 | E' | |
| 26 | Asymmetrical Stretching | 2609.1 | 295.3 | E' | |
| 29 | Asymmetrical Stretching | 3629.8 | 43.7 | E' | |
| 30 | Asymmetrical Stretching | 3629.8 | 43.7 | E' |
There were 7 distinct peaks: 4 degenerate pairs (21&22, 23&24, 25&26, 29&30), and peaks at 408.6 cm-1, 729.4 cm-1, and 936.1 cm-1. The other vibrational modes were of too low an intensity to consider. There were 30 vibrational modes due to 3 x 12 - 6 = 30.
Phosphazene
Low frequencies --- -4.5473 -4.5473 -4.3025 -0.0063 -0.0061 -0.0042
Low frequencies --- 36.2412 36.2412 36.8539
1 2 3
E" E" A2"
Frequencies -- 36.2368 36.2368 36.8539
4 5 6
A1" E' E'
Frequencies -- 115.4255 150.6916 150.6916
7 8 9
A1' E" E"
Frequencies -- 168.1668 191.8803 191.8803
10 11 12
E' E' E"
Frequencies -- 211.1592 211.1592 311.2966
13 14 15
E" A2' E'
Frequencies -- 311.2966 311.5826 324.6814
16 17 18
E' A1' A2"
Frequencies -- 324.6814 343.1592 374.3319
19 20 21
E' E' E"
Frequencies -- 506.3861 506.3861 549.6213
22 23 24
E" A2" A1'
Frequencies -- 549.6213 607.6235 654.3398
25 26 27
A1' E' E'
Frequencies -- 769.0054 855.2266 855.2266
28 29 30
A2' E' E'
Frequencies -- 1124.7577 1224.1376 1224.1376
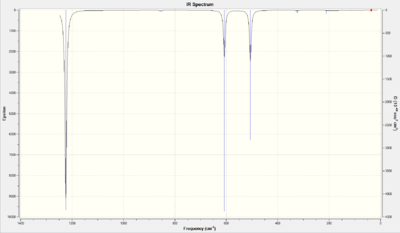
| Number | Form of the Vibration | Frequency | Intensity | Animation | Symmetry Point Group |
|---|---|---|---|---|---|
| 3 | Rocking | 36.9 | 0.3 | Visualise | A2" |
| 5 | In-plane Scissoring (Bending motion) | 150.7 | 0.0 | Visualise | E' |
| 6 | In-plane Scissoring (Bending motion) | 150.7 | 0.0 | Visualise | E' |
| 10 | Wagging | 211.2 | 4.4 | Visualise | E' |
| 11 | Wagging | 211.2 | 4.4 | Visualise | E' |
| 15 | Wagging | 324.7 | 4.5 | Visualise | E' |
| 16 | Wagging | 324.7 | 4.5 | Visualise | E' |
| 18 | Rocking | 374.3 | 0.6 | Visualise | A2" |
| 19 | Rocking | 506.4 | 358.8 | Visualise | E' |
| 20 | Rocking | 506.4 | 358.8 | Visualise | E' |
| 23 | Rocking | 607.6 | 666.6 | Visualise | A2" |
| 26 | In-plane Scissoring | 855.2 | 7.3 | Visualise | E' |
| 27 | In-plane Scissoring | 855.2 | 7.3 | Visualise | E' |
| 29 | In-plane Scissoring | 1224.1 | 1333.8 | Visualise | E' |
| 30 | In-plane Scissoring | 1224.1 | 1333.8 | Visualise | E' |
There were three distinct peaks: 2 degenerate pairs (19&20, 29&30), and one peak at 607.6 cm-1. There were 30 vibrational modes due to 3 x 12 - 6 = 30.
Analysis
The main interest in the IR spectra was the frequency given by the components in the six membered ring, i.e. (C=C) in benzene, (B-N) in borazine, and (P-N) in phosphazene. Literature values for the stretching motion eare 1495 cm-1 (C=C), 1435 cm-1 (B-N)[5], 1293 cm-1 (P-N)[6].
Compared to the literature values there was an error of +18 cm-1 for benzene, +50 cm-1 for borazine, and -69 cm-1 for phosphazene. The shifts in the frequencies were low enough.
Comparing the three frequencies, the benzene ring components produced the highest peak, then the borazine components, and then phosphazene components. These were good comparisons as the stretching peaks are of similar values. C-C is fairly similar to B-N as the three atoms are all in the same period and are in neighbouring groups; i.e. isoelectronic. P-N is however different as the p-d interactions increase the aromaticity of phosphazene and phosphorus is in Period 3, Group 15, the same group as nitrogen. This is why the P-N stretching peak is situated at a lower frequency than the other two.
Conclusion
It would have been interesting investigating other six-membered inorganic rings such as (NSF)3, or 1,2-azaborine[7] and other derivatives of borazarene comparing the parallels between the two isoelectronic rings (benzene, and borazene).
A better basis set should have been used to optimise the geometries; although the geometries agreed with the literature symmetries were lost during the calculations.
The isoelectronic nature of benzene and borazine were successfully determined through optimisation, MO, NBO, and IR analyses. The phosphazene required a more advanced algorithm for more accuracy. Perhaps the chlorine atoms could have been substituted with a smaller atom, say hydrogen for further analysis. The calculations were fairly accurate, the investigation was a success.
References
- ↑ K. Burke, J. Werschnik, E.K.U. Gross, "Time-dependent density functional theory: Past, present, and future", J. Chem. Phys., 2005, 123, 123-131DOI:10.1063/1.1904586
- ↑ M.S. Schuurman, W.D. Allen, H.F. Schaefer III, "The ab initio limit quartic force field of BH3", J. Comp. Chem., 2005, 26 (11), 1106-1112DOI:10.1002/jcc.20238
- ↑ M. Atanasov, D. Reinen, J. Phys. Chem. A, 2001, 105 (22), 5467 DOI:10.1021/jp004511j
- ↑ D. W. Bennett, T. A. Siddiquee, D. T. Haworth, S. E. Kabir, F. K. Camellia, J. Chem. Cryst., 2004, 34 (6), 353DOI:10.1023/B:JOCC.0000028667.12964.28
- ↑ J. Li, S. Bernard, V. Salles, C. Gervais, P. Miele, "Preparation of Polyborazylene-Derived Bulk Boron Nitride with Tunable Properties by Warm-Pressing and Pressureless Pyrolysis", Chem. Mater., 2010, 22, 2010-2019DOI:10.1021/cm902972p
- ↑ H. Baran, E.Cil, M. Arslan, "Synthesis and Characterization of Cycloamino and Oxime-Linear Phosphazenes", Russ. J. Inorg. Chem., 2007, 52(12) 1892-1895DOI:10.1134/S0036023607120157
- ↑ M. J. S. Dewar, P. A. Marr, "A Derivative of Borazarene", J. Am. Chem. Soc., 1962, 84, 3782DOI:10.1021/ja00878a045