Rep:Mod:holyzarquonsingingfish
Module 1
The Hydrogenation of Cyclopentadiene Dimer
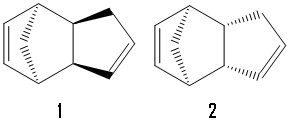
There are two possible conformations for the cyclopentadiene dimer, 1 and 2 with the exo form 2 predominating. Optimising the geometry of each conformation using an MM2 force field gives a total energy of 31.9 kcal/mol for 1 and 34.0 kcal/mol for 2 showing conformer 1 to be the more thermodynamically stable. Since the less thermodynamically stable conformer predominates the reaction is shown to be kinetically controled.
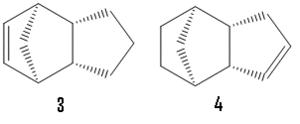
When dimer 2 is hydrogenated only one double bond will hydrogenate initially forming dihydro derivative either 3 or 4 before proceeding though to the tetrahydro devivative. Using the same technique as above total energies of 35.9 kcal/mol and 31.2 kcal/mol are derived for 3 and 4 respectively with the greatest contributions to the differing energies coming from bending and non-1,4 van der waals energies (differences of 4.5 kcal/mol and 0.8 kcal/mol respectively). This allows us to predict that 4 will be the major dihydro derivative product under thermodynamic conditions.
Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD+ analogue)
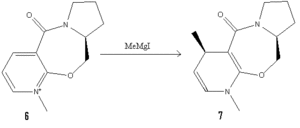
A model (MM2) of prolinol derivative 5 with energy 26.4 kJ/mol as seen below shows a dihedral angle between the carbonyl and aromatic ring of 24º.
derivative 5 |
When 5 reacts with a gringard reagent the benzene ring alkylates with absolute stereochemistry 6. Producing this stereochemistry involves addition of the methyl group onto the face of the benzene ring which brings the reagent closest to the out of plane carbonyl. It is therefore likely that the reaction proceeds via complexation of the magnesium atom to the carbonyl oxygen.[1]
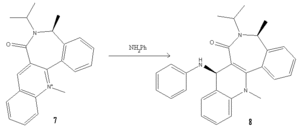
In the case of the model (MM2) of piridinium derivative 7 with energy 15.9kJ/mol as seen below the dihedral angle between the carbonyl and the aromatic ring is even greater at -43º.
derivative 7 |
When 7 is reacted with aniline derivative 8 is formed. In contrast to the case of derivative 5 analine adds away from the carbonyl of 7 acting under steric control. [2]
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
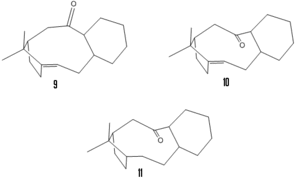
An intermediate in the synthesis of taxol can be synthesised in one of two isomers 9 and 10 however on standing it will isomerise leaving only the more stable isomer. Modelling both isomers (MM2) returns an energy of 64.7 kcal/mol for isomer 9 and 49.9 kcal/mol for isomer 10. Isomer 10 is therefore the more stable with a much lower bending energy. This is most likely due to the conformation of the attached cyclohexane. In isomer 10 this is able to take the lower energy boat conformation whereas in isomer 9 the ring is forced into the highly strained twist-boat conformation.[3]
The double bond in this compound reacts abnormally slowly. When the saturated compound 11 is modelled (MM2) it is found to have a higher energy than the parent alkene. This difference in energy is the olefinic strain which originates in the strain energy of the bridgehead. For this compond the olefinic strain (MM2) is calculated as 21.7 kcal/mol.[4]
How One Might Induce Room Temperature Hydrolysis of a Peptide
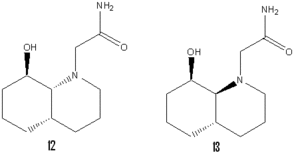
Amides normally hydrolyse very slowly at room temperature with an average half life of 500 years. Amides 12 and 13 however will hydrolyse within a reasonable experimental time frame. 12 hydrolyses the fastest with a half life of just 21 minutes compared to the 840 minute half life of amide 13. Both amides react so quickly because the conformation of the molecule holds the OH group in the correct position relative to the carbonyl for the reaction to proceed. The difference in speed between the two isomers comes from the different conformers which they can adopt. Calculating using molecular modelling (MM2) we see that both isomers prefer to adopt a conformation in which the ring N-substituent is equatorial to the ring with an energy difference between conformations of 2.94 kcal/mol and 6.32 kcal/mol for 12 and 13 respectively. The difference in reaction speed is explained by the fact that the reactive conformer for 12 is the equatorial conformer whereas for 13 the reactive conformer is the axial introducing an energy barrier to hydrolysis.[5]
| Nitrogen position | Equatorial | Axial | ||||||
| Amide 12 |
|
| ||||||
| Amide 13 |
|
|
Regioselective Addition of Dichlorocarbene
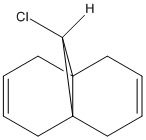
The molecular orbitals of compound 12 were calculated using the HF/STO-3G self-consistant-field MO method after first optimising the geometry using MM2. The move from a classical to a quantum mechanical approach results in minor changes in the geometry of the compound. Particularly a flattening of the ring exo to the chlorine atom with all four non-zero internal dihedral angles reducing from ~10 to ~8 degrees/angstrom. The calculated frontier orbitals are as follows:
 |
 |
 |
 |
 |
Since the electron density in the highest ocupied molecular orbital is mainly concentrated around the double bond exo to the chlorine we can expect this to be the site of electrophilic attack.
A version of compound 12 with the bond exo to the chlorine hydrogenated was otimised in the same manner as the dialkene and the vibrational modes of both complexes were calculated using the b3lyp/6-31G(d) method. The models were visulised using gaussview and key vibrations identified. The alkene has two c=c stretching vibrations. The bond exo to the chlorine vibrates at 1760 cm-1 with an infrared intensity of 3.90. The bond anti to the chlorine vibrates at 1741 cm-1 with an infrared intensity of 4.14. The equivalent bond in the hydrogenated version also vibrates at 1741 cm-1 with an reduced infrared intensity of 3.20. There are no pure C-Cl vibrations in either molecule but there is a vibration in each which contains a significant C-Cl streching componant and has a large intensity. This lies at 772.6 cm-1 with an infrared intensity of 25.2 in the dialkene and at 757.7 cm-1 with an infrared intensity of 27.4 in the hydrogenated product indicating a slight weakening of the C-Cl bond upon hydrogenation.
Mini project

This photocycloaddition and reduction was reported by L.M.Tedaldi and J.R. Baker [6]. Although it is shown here as a two step reaction for clarity the reduction takes place in-situ as part of a one pot reaction to prevent the photochemical degedation of the product keytone. The reaction product is assigned by them as the isomer (1RS, 5RS, 7SR, 8SR) 2-oxa-tricylo[5.3.0.0]decan-8-ol and both 13C and 1H NMR results are given. This geometry is confirmed here by calculation of the 13C NMR of this isomer and isomers 2, to confirm the stereochemistry of the reduction, and 3, to confirm the regioselectivity of the cycloaddition.

The experimental NMR assignment is as follows 13C NMR (125MHz, CDCl3, δ) 91.58 (C1), 89.11 (C4), 68.23 (C9), 43.25 (C5), 40.70 (C7), 32.45 (C8), 31.79 (C3), 31.21 (C2), 17.84 (C6)[6]
The calculated NMR for isomer 1 13C NMR (CDCl3, δ) 92.02 (C1), 72.18 (C4), 66.13 (C9), 47.02 (C5), 43.39 (C7), 39.52 (C3), 34.92 (C2), 32.74 (C8), 18.95 (C6) (unable to publish)
The calculated NMR for isomer 2 13C NMR (CDCl3, δ) 82.10 (C1), 72.90 (C4), 56.94 (C9), 39.52 (C5), 33.95 (C7), 29.60 (C3), 25.48 (C2), 23.55 (C8), 18.71 (C6) (unable to publish)
The calculated NMR for isomer 3 13C NMR (CDCl3, δ) 87.90 (C1), 70.48 (C4), 59.11 (C9), 56.21 (C5), 36.37 (C1), 33.47 (C2), 32.98 (C8), 30.81 (C6), 28.15 (C7) (unable to publish)
Unfortuneately calculated the NMRs for isomers 1 and 2 were run with a conformational error. Most probably the positioning of carbon 3 with respect to the ring. However, the chemical shift of carbon 1 still suggests that the isomer assigned in the paper is the correct one.
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838
- ↑ Leleu, Stephane; Papamicael, Cyril; Marsais, Francis; Dupas, Georges; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928
- ↑ J. G. Vinter and H. M. R. Hoffman, J. Am. Chem. Soc., 1974, 96, 5466
- ↑ Wilhelm F. Maier and Paul von Raguc Schleyer, J. Am. Chem. Soc., 1981, 103, 1891
- ↑ M. Fernandes, F. Fache, M. Rosen, P.-L. Nguyen, and D. E. Hansen, 'Rapid Cleavage of Unactivated, Unstrained Amide Bonds at Neutral pH', J. Org. Chem., 2008, 73, 6413–6416
- ↑ 6.0 6.1 Lauren M. Tedaldi and James R. Baker, Org. Lett., Article ASAP, DOI: 10.1021/ol8026494, Publication Date (Web): January 22, 2009 Cite error: Invalid
<ref>tag; name "cyclo" defined multiple times with different content
