Rep:Mod:holbein16
Module 1: The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations
Objectives
The aim of this experiment is to use molecular mechanics to predict the stereochemistry and regioselectivity for a range of molecules. In addition to this a mini project is carried out using semi-empirical and DFT molecular orbital theory to investigate the stereoselectivity of an imino Diels-Alder reaction taken from experimental literature.
The Hydrogenation of Cyclopentadiene Dimer
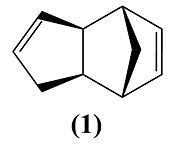
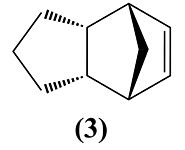
Cyclopentadiene dimerises to produce specifically the endo dimer 2 rather than the exo dimer 1. Hydrogenation of this dimer proceeds to give initially one of the dihydro derivatives 3 or 4.
 |
 |
 |
 |
Dimerisation of Cyclopentadiene
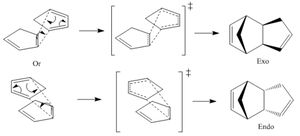
Cyclopentadiene dimerises to form a dimer via the mechanism of the [π4+π2] Diels-Alder cycloaddition reaction (shown on the right). This can theoretically result in either the exo product (molecule 1) or the endo product (molecule 2).
The endo product is favoured and so is the only one which is formed. This is known as the endo dimer is less strained within its conformation and therefore more thermodynamically stable (thermodynamic product). This means that the exo dimer is the kinetic product by it being higher in energy. The endo product is also favoured due to it's formation being faster due to a lower energy transition state because of secondary orbital interaction.[1]
| Molecule | Total Energy (kcal/mol) |
|---|---|
| 1 (Exo Dimer) | 31.88 |
| 2 (Endo Dimer) | 34.01 |
Hydrogenation
Table 2 shows the total energy and individual contributions between molecules 3 and 4. Molecule 4 is less hindered than molecule 3 by it having a total energy of 31.1594 kcal/mol when molecule 3 has a total energy of 35.6989 kcal/mol. From this it can be deduced that molecule 4 is more thermodynamically stable and this is mainly due to molecule 4's bend value being 5.2819 kcal/mol more stable. This therefore means more bend strain was released within the hydrogenation of creating molecule 4 to that of molecule 3.
So from this data we can conclude that molecule 4 is theoretically more likely to be the product of the hydrogenation of the cyclopentadiene dimer.
| Relative Contributions | Molecule 3 Energies (kcal/mol) | Molecule 4 Energies (kcal/mol) |
|---|---|---|
| Stretch | 1.3040 | 1.0899 |
| Bend | 19.8180 | 14.5361 |
| Torsion | 10.8217 | 12.5062 |
| 1,4 VDW | 5.6307 | 4.5110 |
| Total Energy | 35.6989 | 31.1594 |
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
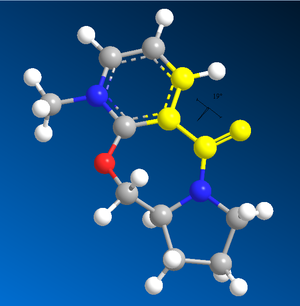
You cannot include the MeMgI component (Grignard reagent) for the MM2 energy minimisation due to Magnesium not being supported by ChemBio3D Ultra. However the addition of MeMgI would increase the total energy of the molecule.
The MMFF94 energy minimisation has a flaw by the calculation going to a local energy minimum and not a universal one. Therefore the conformation of the molecule after the MMFF94 calculation might not be the lowest energy conformation. To get around this problem I carried out an MMFF94 energy minimisation on molecules 5 and 7, noted down the total energy and dihedral angle (shown in the image on the right), moved multiple atoms and carried out the minimisation again. This was done a total of 6 times and the lowest energy was taken (with its respective angle).
| Molecule | Total Energy (kcal/mol) | Dihedral Angle |
|---|---|---|
| 5 | 57.4193 | 6.94 o |
| 7 | 98.3665 | -35.69 o |
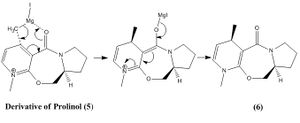
Molecule 5 is an optically active derivative of Prolinol. When it is reacted with methyl magnesium iodide it gives product 6, which is shown within the mechanism on the right. The origin of stereocontrol within this reaction is determined by the coordination between the electronegative oxygen from the carbonyl group and the electropositive Mg of the Grignard reagent, which takes place within a mechanism involving a 6 electron pericyclic transition state.
Also from the results in table 3 it can be seen that the carbonyl bond is 6.94 ° above the aromatic ring. Therefore the MeMgI attacks molecule 5 from above and the addition of the methyl to the molecule would also happen above the ring due to the coordination[2]. This therefore explains the stereochemistry of molecule 6 and thus the stereocontrol within this reaction.
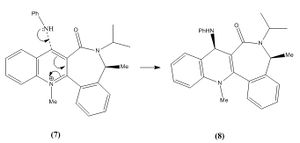
A similar reaction of another pyridinium ring (molecule 7) reacting with aniline was also analysed for its stereocontrol (mechanism on the right).
The reason for stereocontrol within this reaction is due to the repulsions between the lone pairs on the aniline nitrogen and the oxygen on the carbonyl group. In addition to this the relative position of the carbonyl group affects the direction at which the aniline attacks molecule 7. Also steric hindrance between the carbonyl and large phenyl group influence the selectivity. From the results in table 3 it can be seen that the carbonyl bond is 35.69 ° below (-35.69 above) the aromatic ring. This means that the aniline group would attack from the top, which gives the stereospecific conformation of molecule 8.
| Molecule 5 | Molecule 6 | Molecule 7 | Molecule 8 | ||||||||||||
|
|
|
|
We can improve the simple models of the MM2 or MMFF94 minimizations by using the MOPAC/PM6 method since it takes into account electronic structure and molecular orbitals, which leads to more accurate energies and conformations.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
A key intermediate within the total synthesis of Taxol [3] are the atropisomers (9 and 10) shown below. They show a type of stereoisomerism because the rotation about single bonds are hindered, which is due to the steric barrier of rotation being too large for interconversion between the two isomers and therefore both of the conformations are isolated.
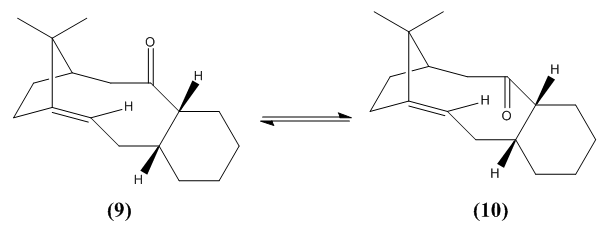
From studying table 4 below it can be deduced that molecule 10, which has the carbonyl group pointing down is thermodynamically more stable than molecule 9. This is seen in both MM2 and MMFF94 minimisations by molecule 10 being 10.0392 kcal/mol lower in energy than molecule 9 within the MM2 calculation and 22.1336 kcal/mol in the MMFF94 calculation.
| Molecule | MM2 Total Energy (kcal/mol) | MMFF94 Total Energy (kcal/mol) |
|---|---|---|
| 9 | 54.3889 | 82.7068 |
| 10 | 44.3497 | 60.5732 |
| Molecule 9 | Molecule 10 | ||||||
|
|
The alkene reacts slowly within both conformations due to it being hyperstable[4]. This is due to it being a hyperstable alkene (or known as a hyperstable olefin) and occurs when the olefin strain energy is negative. This energy is normally positive within alkenes and is negative here because the interactions between the hydrogens on the alkene are stabilising the double bond, which is known as the 1,3-effect (gecko effect).
Modelling Using Semi-empirical Molecular Orbital Theory
(9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene) was drawn on ChemBio3D Ultra and the conformation was minimised by the MM2 calculation, which gave the total energy of 17.8967 kcal/mol. Molecule 12 was then again minimised using the MOPAC/PM6 method.
The addition of dichlorocabene to molecule 12 (shown below) demonstrates high π-selectivity by the mono-adduct (syn-trichloride) and the di-adduct products having the ratio 72:23[5].

From studying the HOMO orbital below it can be seen that the largest amount of electron density is on the syn-alkene, which makes it more nucleophilic than the alternative site site of attack, the electron poor anti-alkene. Since dichlorocarbene is an electrophile it will therefore attack the syn-alkene and not the anti-alkene. In addition to this factor there is a stabilising anti-periplanar interaction amongst the anti-alkene π orbital (HOMO-1) and C-Cl σ* orbital (LUMO+1) which leads to the anti-alkene π orbital to lower its energy relative to the syn-alkene π orbital (HOMO) by 0.08eV[5]. From this it can be deduced that the anti-alkene π orbital is less reactive by it being thermodynamically more stable to that of the syn-alkene π orbital and therefore explains the regioselectivity above.
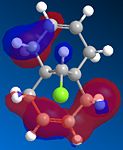 |
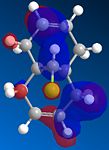 |
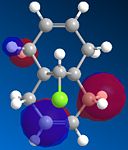 |
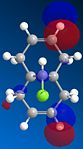 |
 |
Guassview 5.0 was used to calculate the IR spectra of various different derivatives of molecule 12, which is shown below in table 5. The first observation to be made is that the wavenumber for the C-Cl bond stretch within molecule 12 and the monohydrogenated molecule 12 are 770.90 and 779.80 cm-1, which corresponds to the literature value[6] of 600-800 cm-1.
The wavenumbers of the C=C bonds are higher than that of the literature values[6](1620-1680 cm-1) which suggests that the C=C bonds are stronger and more stable in the molecule 12 derivatives since higher wavenumbers mean the bonds are more stable. This extra stability will originate from the rigid structure of the bicyclic compound and the chlorine may donate electron density to the π bonds.
From studying the the IR of molecule 12 one would find that the syn C=C stretch is lower to that of the anti C=C stretch, which would therefore mean that the syn bond is less stable and therefore more reactive than the anti and therefore seems to contradict the evidence from looking at the molecular orbitals. However when we were studying the molecular orbitals we were just taking the π aspect of the bond into account and not the σ contribution. So the overall stability of the syn C=C bond is lower to that of the anti C=C bond, where the de-stability will be due the σ contribution or any other destabilising interactions within the molecule. In addition to this the frequencies of the syn C=C stretch within molecule 12 and the monohydrogenated molecule 12 are very similar to each other, which means that the anti C=C bond does not influence the stability of the syn C=C drastically.
From modifying the substituents on the anti alkene from the =C-H group to =C-OH, =C-CN, =C-BH2 and =C-SiH3 groups the effects on the Cl-C and C=C frequencies could be investigated. From this we can initially see that the syn C=C stretch and C-Cl stretch was not greatly altered by any of the substituents being added. However the anti C=C bond does change significantly with the various substituents.
The largest change is with the BH2 group and this will be due to it acting as Lewis acid and accepting electrons from the π bond to go into its low lying unoccupied p-orbital which would weaken the alkene bond. This will be the same reason to why the anti alkene bonds stability is lowered with the silyl group but the affect will be less due to the electrons being promoted to silicon's d-orbitals, which are higher in energy and more diffuse, thus less weakening. The cyano substituent also de-stabilises the anti C=C due to it again withdrawing electrons by the nitrogen by being more electronegative than carbon. The hydroxy group however stabilises the the anti alkene by oxygen donating electrons via resonance to the C=C bond and therefore strengthening it.
| Molecule | |||
|---|---|---|---|
| C-Cl Stretch | Anti C=C Stretch | Syn C=C Stretch | |
| Frequency (cm-1) | 770.90 | 1737.06 | 1757.35 |
| Intensity | 3.9367 | 4.1981 | 60.5732 |
| C-Cl Stretch | Anti C=C Stretch | Syn C=C Stretch | |
| Frequency (cm-1) | 779.80 | n/a | 1753.80 |
| Intensity | 21.4817 | n/a | 5.0431 |
| C-Cl Stretch | Anti C=C Stretch | Syn C=C Stretch | |
| Frequency (cm-1) | 765.29 | 1753.03 | 1757.76 |
| Intensity | 6.6520 | 59.0175 | 37.6681 |
| C-Cl Stretch | Anti C=C Stretch | Syn C=C Stretch | |
| Frequency (cm-1) | 765.79 | 1706.31 | 1756.54 |
| Intensity | 8.0676 | 11.4291 | 4.8241 |
| C-Cl Stretch | Anti C=C Stretch | Syn C=C Stretch | |
| Frequency (cm-1) | 759.04 | 1657.21 | 1756.55 |
| Intensity | 3.8281 | 131.9383 | 4.5261 |
| C-Cl Stretch | Anti C=C Stretch | Syn C=C Stretch | |
| Frequency (cm-1) | 763.822 | 1690.33 | 1756.24 |
| Intensity | 17.4369 | 19.038 | 5.5053 |
Structure based Mini project using DFT-based Molecular orbital methods: Indium trichloride (InCl3) catalyzed imino Diels-Alder reactions
The mini project will investigate the indium trichloride (InCl3) catalyzed imino Diels-Alder reaction[7] between N-benzylideneaniline and cyclohex-2-enone, which produces two different stereoisomers.
The aim of this project is to differentiate between the two stereoisomers by using computational calculations of various spectroscopy techniques. From the spectra we will be able to make comparisons between the calculated and experimental data. In addition to this molecular modelling calculations will be made to try and explain the regioselectivity and the ratios of the synthesised stereoisomers for the reaction.
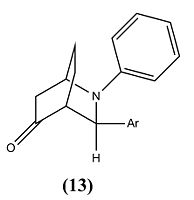
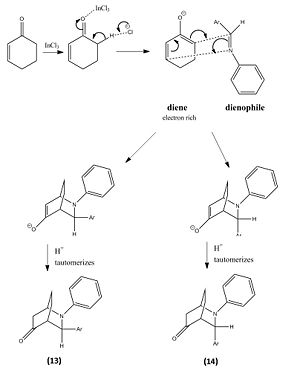
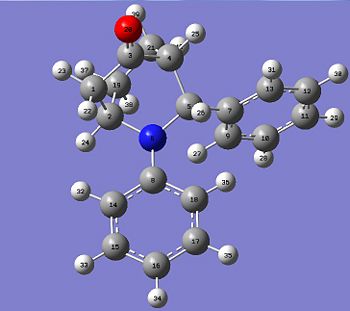
The reaction involved reacting with at room temperature for 24 hours, which produced molecule 13 and 14 in a hetero Diels-Alder reaction, however within the literature they envisaged the formation of phenanthridinone derivatives 15 and 16. This happened due to chemioselectivity within the first step of the mechanism by the indium trichloride (InCl3) coordinating strongly with the cyclohexadienolate ion. This lead to the cyclohex-2-enone becoming electron rich and therefore reacting as the diene and the imine acting as the dienophile, which was the opposite to the proposed roles of both reactants.
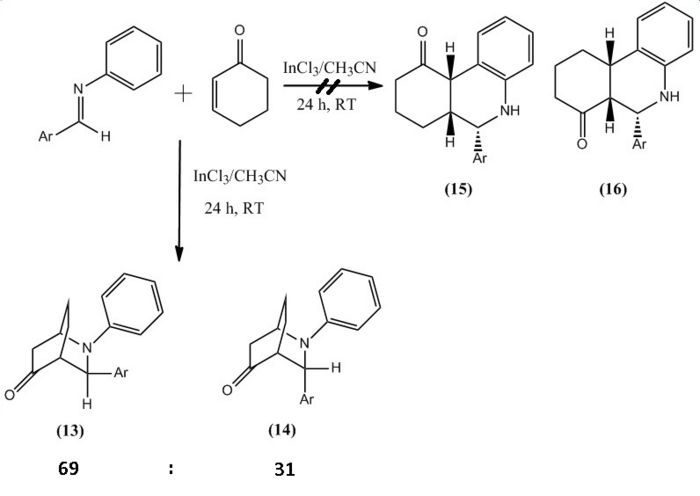
| Product 13 | Product 14 | ||||||||
|
|
From this reaction two other possible regioisomers were theoretically possible however none were formed due to how the mechanism took place. The image below shows the other possible mechanism which would lead to the other 2 regioisomers for this reaction. However the 1,2-alkene bond on the cyclohexadienolate ion is highly delta negative due to the O- donating a significant amount of electron density to it and therefore the electrons within the C=N π bond attacking 1,2-alkene is not likely. This argument is further strengthened by the 1,2-alkene having a larger amount of electron density in the HOMO compared to the 5,6-alkene, which is the other possible site the cyclohexadienolate ion could attack the imine from. A final factor to why the alternative reaction does not take place is due to the carbon within the C=N bond having more electron density in the LUMO to that of the nitrogen. Thus makes the carbon a more likely place for the electrons to attack.
 |
 |
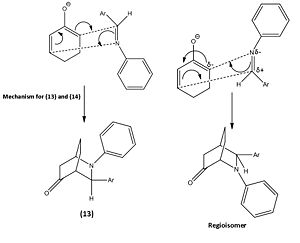 |
The ratio of molecule 13 to 14 is 69:31[7]. From studying this it was deduced that the molecules stabilities could play a vital role into an explanation of why equal amounts of products were not synthesised. However by looking at table 6 and 7 this is obviously not the case. Therefore the reason will most likely be that the transition state of molecule 13 is more thermodynamically stable at room temperature and so 13 is favoured over 14.
| Relative Contributions | Molecule 13 Energies (kcal/mol) | Molecule 14 Energies (kcal/mol) |
|---|---|---|
| Stretch | 2.0824 | 2.1202 |
| Bend | 9.2284 | 9.0755 |
| Torsion | -5.0755 | -5.2468 |
| 1,4 VDW | 21.4885 | 21.4109 |
| Total Energy | 27.5287 | 27.1443 |
| Molecule | Total Energies (kcal/mol) |
|---|---|
| Molecule 13 | 39.7093 |
| Molecule 14 | 41.1574 |
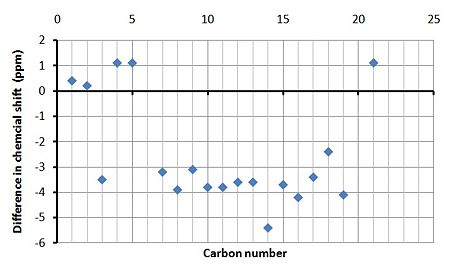
From analysing the 13C NMR data below it can be deduced that it is not possible to clearly distinguish between molecule 13 and 14 by using 13C NMR spectroscopy. This will also be the case with 1H NMR since the chemical shifts will be slightly different and therefore unnecessary to analyse. However it is possible to compare it to other experimental values and so distinguish which NMR belongs to which isomer, however this means relying on other academics experimental data and this is not recommended or ideal.
From table 8 and 9 below the simulated 13C NMR spectra can be compared to that of the experimental NMR and therefore does support the structural assignment in the paper. In spite of this though the simulated spectra did not totally match the experimental due to various reasons. The main factor is that some of the carbon peaks overlapped with other carbons with similar chemical shifts and since you cannot carry out integration on 13C NMR the experimental data did not give the amount of carbons responsible for each peak. This meant that in both experimental cases only 15 peaks were recorded however in the simulated cases 19 were calculated (since chemical formula is C19H14NO). So below some experimental peaks have been assigned multiple carbon atoms from the simulated spectra which are most likely contributing to them.
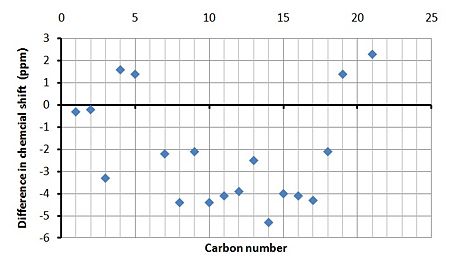
By studying the graphs showing the the difference in the calculated and experimental chemical shifts it it clear that the majority of the calculated peaks have a lower chemical shift in both cases. This will most likely be due to other conformers/chemicals within the experimental NMR sample and that the calculations are approximations and therefore not perfect.
| Carbon number | Calculated chemical shift (ppm) | Experimental chemical shift[7] (ppm) |
|---|---|---|
| 3 | 210.3 | 213.6 |
| 8 | 143.7 | 148.1 |
| 7 | 137.8 | 140.0 |
| 17 | 125.7 | 130.0 |
| 12, 15, 10 | 125.4, 125.3, 124.9 | 129.3 |
| 11 | 123.7 | 127.8 |
| 9, 13 | 123.0, 122.6 | 125.1 |
| 16 | 113.5 | 117.6 |
| 18, 14 | 110.9, 107.7 | 113.0 |
| 5 | 63.7 | 62.3 |
| 4 | 52.5 | 50.9 |
| 2 | 47.9 | 48.1 |
| 1 | 41.9 | 42.2 |
| 19 | 27.3 | 25.9 |
| 21 | 18.6 | 16.3 |
| Carbon number | Calculated chemical shift (ppm) | Experimental chemical shift[7] (ppm) |
|---|---|---|
| 3 | 208.3 | 211.8 |
| 8 | 143.8 | 147.7 |
| 7 | 138.9 | 142.1 |
| 17 | 125.8 | 129.2 |
| 12, 15, 10 | 125.3, 125.2, 125.1 | 128.9 |
| 11 | 123.7 | 127.5 |
| 9, 13 | 122.4, 121.9 | 125.5 |
| 16 | 113.4 | 117.6 |
| 18, 14 | 110.8, 107.8 | 113.2 |
| 5 | 66.9 | 65.8 |
| 4 | 53.2 | 52.1 |
| 2 | 48.6 | 48.4 |
| 1 | 46.2 | 45.8 |
| 19 | 25.5 | 29.6 |
| 21 | 23.7 | 22.6 |
 |
 |
 |
 |
 |
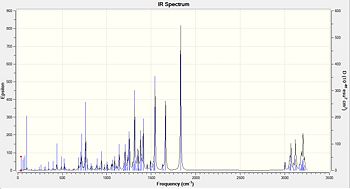
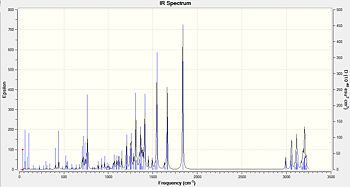
Again it is not possible to distinguish between the two isomers by looking at the IR spectra. However once again it is possible to compare the calculated spectra to the experimental in order to see if it confirms the structural assignment in the paper. Within table 10 and 11 it can be seen that some calculated peaks are exactly the same to the experimental peaks. Although there are other peaks that do not match up and this will be to some bug within the calculation or not a pure product within the experimental.
| Functional group | Calculated frequency (cm-1) | Experimental frequency[7] (cm-1) | Literature value[6] (cm-1) |
|---|---|---|---|
| C=C aromatic | 1492.26 | 1497 | 1400-1600 |
| C=O carbonyl | 1830.22 | 1721 | 1670 - 1820 |
| C-H Alkane | 3003.66 | 2936 | 2850 - 3000 |
| OH or NH by-products | too large a frequency | 3382 | 3200 - 3600(OH) or 3300 - 3500(NH) |
| Functional group | Calculated frequency (cm-1) | Experimental frequency[7] (cm-1) | Literature value[6] (cm-1) |
|---|---|---|---|
| C=C aromatic | 1492.38 | 1491 | 1400-1600 |
| C=O carbonyl | 1835.92 | 1722 | 1670 - 1820 |
| C-H Alkane | 2992.01 | 2928 | 2850 - 3000 |
| OH or NH by-products | too large a frequency | 3392 | 3200 - 3600(OH) or 3300 - 3500(NH) |
 |
 |
Spectroscopy techniques that will differentiate the isomers
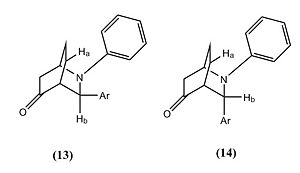
Nuclear Overhauser Effect Spectroscopy (NOESY) would differentiate between the two isomers. This would be possible due to it being able to measure the distance between two hydrogens within the structure. An example of how this could differentiate between the isomers 13 and 14 is shown on the right.
Another spectroscopic technique would be X-ray crystallography since again it would give you the angles and distances between the carbons and hydrogens within the structure and this was how the structure was ascertained within the literature.
References
- ↑ P. Caramella, P. Quadrelli, L. Toma., J. Am. Chem. Soc., 2002, 124, 7, pp. 1130–1131.[1]
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, pp. 838.[2]
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, pp. 319.[3]
- ↑ W.F. Maier, P.V.R. Schleyer, J. Am. Chem. Soc., 1981, 103, pp. 1895.[4]
- ↑ 5.0 5.1 B. Halton, S. G. G. Russell. J. Org. Chem., Vol.56,No.19, 1991, pp. 5553–5556.[5]
- ↑ 6.0 6.1 6.2 6.3 IR Correlation Table.[6]
- ↑ 7.0 7.1 7.2 7.3 7.4 7.5 7.6 G. Babu, P. T. Perumal, Vol. 54, 1998, pp. 1627-1638.[7]
- ↑ Digital repository NMR prediction for molecule 13.[8]
- ↑ Digital repository NMR prediction for molecule 14.[9]