Rep:Mod:hnt14Y3
Introduction
In this project, a series of pericyclic reactions were explored. Diels-Alder cycloaddition, chelotropic and electrocyclic reactions were all studied. A Diels-Alder cycloaddition between a diene and a dienophile can be normal or inverse demand. A normal demand reaction occurs when the HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) of a transition state or product are formed from the diene HOMO and the dienophile LUMO. Inverse demand occurs as a result of interaction between the diene LUMO and dienophile HOMO. Both inverse and normal demand Diels-Alder cycloaddition were under investigation.
The reactants, products and transition states were built in GaussView and optimised using the semi-empirical PM6 method and Density Functional Theory (DFT) B3LYP method. This allowed the MOs (molecular orbitals) of each to be visualised and their relative energy levels to be determined. The MOs are built by linearly combining basis sets. Hence, this is a quantum mechanical approach to generating MOs. The PM6 optimisation is faster and thus offers an initial optimisation which can be more accurately optimised using the more complex B3LYP where necessary.
A potential energy surface (PES) shows how the potential energy of a system changes along numerous reaction coordinates. Along a particular coordinate, the transition state is a maximum, where the gradient is zero. Transition states occur at maxima because they are high in energy and unstable. However, the transition state is also a minimum in all other directions, thus making it a saddle point. The reactants and products along a reaction coordinate will be minima, also with a zero gradient. As the first derivative is zero in both cases, a second derivative (the curvature) is determined to distinguish between maxima and minima. The second derivative will have a negative value for a maximum and a positive value for a minimum. Thus, when trying to locate a transition state in GaussView by running a frequency calculation, a single negative frequency value will be an indication that a transition state has been found.
Nf710 (talk) 09:19, 23 March 2018 (UTC) Your discussion of the levels of theory is quite brief and more detail/ equations could have happened here. And remember to say that when on the PES you should be in 3N-6 coords.
Question 1ː Reaction of Butadiene with Ethylene
(Fv611 (talk) Very good job across the whole section. Well done.)
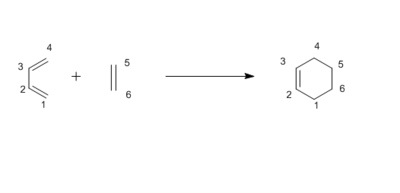
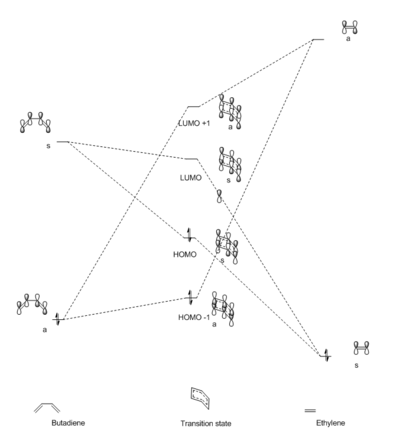
Figure 1 shows the reaction scheme for the cycloaddition between butadiene and ethylene. In Figure 2, an MO diagram is constructed based on the interacting orbitals in the transition state of the Diels-Alder cycloaddition. These were determined by observing the relevant orbitals of the transition state formed from the HOMO and LUMO of each of the reactants in GaussView. The orbitals drawn in the MO diagram in Figure 2 correlate with those extracted from GaussView, which are shown in Table 1. It can be concluded from the resulting MOs in the transition state that only orbitals of the same symmetry are allowed to interact. Thus, there is a symmetry requirement for two interacting orbitals. In the case of orbitals with different symmetry, the interaction is forbidden and the orbital overlap integral will be zero. For orbitals of the same symmetry, the interaction is allowed and the overlap integral is non-zero. The results are summarised in Table 2.
|
|
|
| ||||||||||||
|
|
|
|
| Allowed | Forbidden | Orbital Overlap Integral | |
|---|---|---|---|
| Symmetric-Symmetric | X | Non-zero | |
| Asymmetric-Asymmetric | X | Non-zero | |
| Symmetric-Asymmetric | X | Zero |
In the reaction, the distances between atoms vary depending on whether a bond is being made or broken. Where a bond is being broken, its length will increase in the transition state until the bond eventually breaks. In the case of a bond being made, the distance between the atoms decreases as the bond forms. Where a bond is going from a single bond to a double bond, the bond length shortens and vice versa. The typical bond length for a single sp3-sp3 C-C bond is 1.54 Å [1] and 1.34 Å [1] for a double sp3-sp2 bond. In the transition state, the two bonds being formed are between C4-C5 and C1-C6. Both have a length of 2.11 Å between the carbon atoms in the transition state. This is considerably less than twice the Van der Waals radius of the carbon atom which is 3.4 Å. Hence, it can be concluded that there is an interaction between C4-C5 and C1-C6 in the transition state. In the product, bonds are formed at these sites that have a length of 1.54 Å, as expected for carbon-carbon single bonds. The overall change in bond lengths can be seen in Table 3.
| Butadiene | Ethylene | Transition State | Product | Change in bond | |
|---|---|---|---|---|---|
| C1-C2 | 1.3335 | - | 1.3798 | 1.4926 | Longer |
| C2-C3 | 1.4708 | - | 1.4111 | 1.3331 | Shorter |
| C3-C4 | 1.3334 | - | 1.3798 | 1.4926 | Longer |
| C4-C5 | - | - | 2.1146 | 1.5358 | - |
| C5-C6 | - | 1.3273 | 1.3818 | 1.5376 | Longer |
| C1-C6 | - | - | 2.1149 | 1.5358 | - |
The vibration shown below corresponds to the vibration along the reaction path that occurs at the transition state of the reaction. As the two new bonds at C4-C5 and C1-C6 form at the same time, the reaction is concerted and the formation of the two bonds is synchronous.
Figure 3-Vibration Mode at the Transition State |
Files for the optimised reactants at PM6 levelː Ethylene Optimisation, Butadiene Optimisation
Files for the optimised transition state and the IRC at PM6 level: TS Optimisation,IRC
File for the optimised product at PM6 levelː Product Optimisation
Question 2ː Reaction of Cyclohexadiene and 1,3-Dioxole
(Fv611 (talk) The MO diagram is good, but you should have discussed the differences between the endo and exo conformations in terms of relative TS MO energies.)
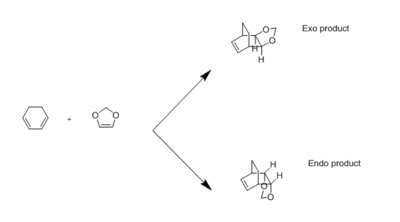
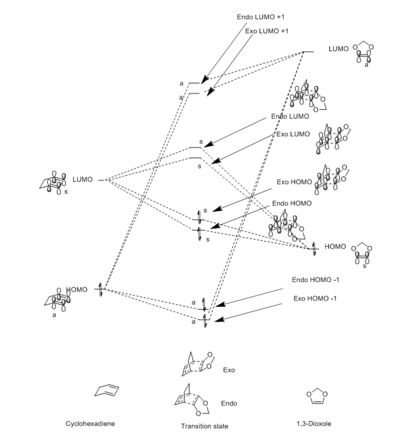
The MO's of both the exo and endo transition states can be seen in Figure 5. The relative energy levels were determined using the B3LYP optimisations of the reactants and transition states in GaussView. The orbitals in Table 4 correlate with the energy levels and MOs in figure 5.
This reaction is an inverse demand Diels-Alder reaction because the HOMOs and LUMOs of both the exo and endo transition states occur as a result of the interaction between the diene (cyclohexadiene) LUMO and the dienophile (1,3-dioxole) HOMO.
|
|
|
|
|
| ||||||||||||||||||
|
|
|
|
|
|
| Adduct | Reaction Barrier (kJ/mol) | Reaction Energy (kJ/mol) |
|---|---|---|
| Exo | 166.30 | -65.15 |
| Endo | 158.51 | -68.75 |
The endo adduct has a lower reaction barrier (due to the endo ts being of lower energy) than the exo adduct, indicating the endo product will be the kinetically favourable product (faster formation). Furthermore, the endo adduct also has a lower reaction energy than the exo adduct, meaning the endo product is also the thermodynamically favourable product. The energies can be seen in Table 5.
The lower energy of the endo ts is due to the secondary orbital interactions arising from orbital overlap between the O p orbital and the diene pi system. TS Stabilisation is hence a result of conjugation. This can only be achieved in the endo conformation, where the orbitals are in the correct orientation for overlap, as opposed to the orbitals in the exo adduct. This is in accordance with the endo rule.
The energies in Table 5 were calculated using the free energies of the reactants, products and transition states of the endo and exo adducts, which can be found in the log files below extracted from GaussView.
Files for the optimised reactants at B3LYP levelː Cyclohexadiene Optimisation, 1,3-Dioxole Optimisation
Files for the optimised transition states at B3LYP levelːExo TS Optimisation, Endo TS Optimisation
Files for the IRCs of the optimised transition states at PM6 levelː Exo IRC, Endo IRC
Files for the optimised products at B3LYP levelː Exo Product Optimisation, Endo Product Optimisation
Nf710 (talk) 09:22, 23 March 2018 (UTC) You got your energies correct, and have made some very brief conclusions, but in general there is not enough detail in this section. There are a few things you didnt do, such as properly investigating the electron demand of the reaction.
Question 3ː Diels-Alder vs Chelotropic

The reaction scheme in Figure 6 shows both the Diels-Alder and chelotropic reaction pathways at one of the dienes in xylylene. The Diels-Alder reaction can result in both an endo and exo product.


The IRCs of the exo, endo and chelotropic reactions can be seen in Figures 7, 8 and 9 respectively. These allow the reaction coordinates to be visualised. Xylylene is highly unstable because the ring prefers to be aromatic to lower the molecule's energy. Formation of the products would result in the formation of a benzenoid ring. This 'aromatisation' makes these reactions favourable and results in overall stabilisation. This can be observed in the IRCs, where the bond lengths in the six-membered ring become equal throughout the reaction, indicating the ring is aromatic.
| Adduct | Reaction Barrier (kJ/mol) | Reaction Energy (kJ/mol) |
|---|---|---|
| Exo | 87.19 | -98.23 |
| Endo | 83.22 | -97.58 |
| Chelotropic | 105.53 | -154.56 |
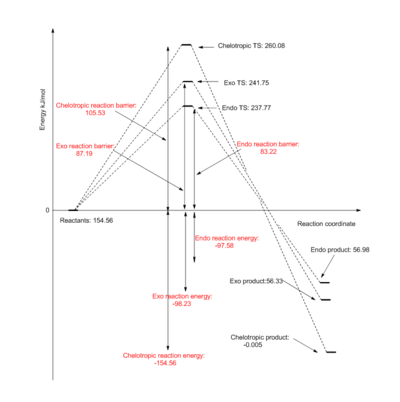
In Table 5, the reaction barriers and energies are calculated for each of endo, exo and chelotropic adducts as before. As can be seen, the exo adduct has a lower reaction energy, making the exo product the more thermodynamically favourable product (compared to the endo product). This is because steric strain is minimised in the exo conformation. On the other hand,the endo adduct affords the lowest reaction barrier due to secondary orbital interactions, making the endo product the fastest forming (kinetically favourable) product. However, the exo and endo energies are only marginally different. In contrast, The chelotropic adduct has a much higher reaction barrier, meaning its formation is considerably slower than both the exo and endo products. The exo and endo adducts form stable six-membered ring transition states (resulting in faster formation), whereas the chelotropic transition state contains a 5-membered ring, making it sterically unfavourable due to ring strain. However, the chelotropic adduct has the lowest reaction energy by far, making it the most thermodynamically favourable product. The driving force is the formation of the double S=O bond compared with the much weaker single S-O bonds. This results in increased stabilisation and thus lower energy (thermodynamically stable) products. The relative reaction profiles for each of the two Diels-Alder reactions and the chelotropic reaction can be seen in figure 10.
Files for the optimsed reactions at PM6 levelː Xylylene optimisation, SO2 optimisation
File for the optimised transition states at PM6 levelː Exo TS optimisation, Endo TS optimisation, Chelotropic TS optimisation
Files for IRCs at PM6 levelː Exo TS IRC, Endo TS IRC, Chelotropic TS IRC
Files for the optimised products at PM6 levelː Exo product optimisation, Exo product optimisation, Chelotropic product optimisation
Reaction at Cyclic Diene
Both the Diels-Alder and chelotropic reactions can occur at the cyclic diene as well. This will also result in exo, endo and chelotropic products. The reaction barriers and energies are reported in Table 6.
| Adduct | Reaction Barrier (kJ/mol) | Reaction Energy (kJ/mol) |
|---|---|---|
| Exo | 121.27 | 22.15 |
| Endo | 113.42 | 17.70 |
| Chelotropic | 142.14 | 48.74 |
As can be observed, the reaction barriers for all three adducts are very high, meaning reaction at the cyclic diene is kinetically unfavourable. Furthermore, the reaction energies of all three adducts are very high, probably due to the non-aromatic product formation. Hence reaction at this diene is also thermodynamically unfavourable.
Files for the optimised transition states at PM6 levelːAlternative exo TS optimisation, Alternative endo TS optimisation,
Alternative chelotropic TS optimisation
Files for the IRCs at PM6 levelː Alternative exo IRC, Alternative endo IRC, Alternative chelotropic IRC
Files for the optimised products at PM6 levelː Alternative exo product optimisation, Alternative endo product optimisation, Alternative chelotropic product optimisation
Future Work

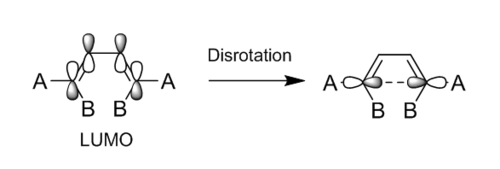
The scheme shown in Figure 11 represents an electrocyclic reaction occuring by disrotation. The bond formation is suprafacial, as seen in Figure 12. The LUMO of the reactant and the HOMO of the transition state that are visualised with Gaussview are consistent with those in figure 12, confirming that the reaction proceeds by disrotation. The visualised MOs are observed in Table 7.
|
|
(This reaction is conrotation under thermal conditions, which it will be under PM6. Confirm this by visualising the IRC Tam10 (talk) 15:46, 16 March 2018 (UTC))
File for optimised reactant at PM6 levelː Reactant optimisation
File for optimised TS at PM6 levelː TS optimisation
File for IRC at PM6 levelː IRC
File for optimised product at PM6 levelː Product optimisation
Conclusion
Gaussview was used to visualise a series of pericyclic reactionsː Diels-Alder, chelotropic and electrocyclic reactions. With Gaussian, molecules and transition states for a large range of reactions can be optimised. Furthermore, MOs and reaction coordinates can be visualised and free energies extracted which can then be used for finding reaction barriers and energies. In this project, this data was extracted for well known reactions. However, the same software and methods can be used for reactions of which the outcome is less well known. This means computational methods can be used to predict the outcome and likelihood of a reaction, giving quantitative results on how a reaction may proceed. Hence, invaluable information can be extracted using these techniques, highlighting the importance of computational chemistry.
References
<references> [1]
