Rep:Mod:hl1910 1

Introduction

Computational chemistry provides an alternative method to experimental chemistry and it's increasingly important in the chemical industry. Not only calculations are quick for relatively simple molecules, but it also avoids the need to be in contact with toxic substances. In addition, dynamic studies of transition states became easily accessible with reasonable accuracy without the need of expensive equipments such as femtosecond laser (typical lifetime of transition state is less than 10^-12

In this course, we're going to familiarise ourselves with Gaussview 5.0, look at the transition states of the Cope rearrangement of 1,5-hexadiene, Diels-Alder cycloaddition and various other thermodynamic properties of those compounds. We'll be using Gaussview to perform optimisations, frequency analysis, intrinsic reaction coordinate (IRC), activation energy calculations, population analysis etc.

Computational chemistry can determine the energy, thermoodynamic and kinetic properties of molecules up to very high degree of accuracy and therefore one can tell, by computing the reaction, whether a reaction is thermodynamically feasible or not, what are the thermodynamic / kinetic products.

The Cope rearrangement of 1,5-hexadiene

The Cope rearrangement of 1,5 hexadiene

The [3,3] sigmatropic rearrangement of 1,5 diene was proposed by Arthur C. Cope in 1940. Under heat, 1,5-hexadiene will undergo a concerted cyclic reaction where the one C-C σ bond is broken on one side and being made at the other end. It has been suggested that the the Cope rearrangement has two possible transition structures: "chair" or "boat". It is also worth noting that since 6π (4n+2 where n=1) electrons are involved and the reactant is heated, the reaction will undergo Hückel suprafacial topology. In the first part of this section, we're going to focus on the possible conformers of 1,5-hexadiene and their energies; and on the second part, we'll turn our attention to the transition state, the "chair" and "boat" transition structures.

Optimisation using HF/3-21G

Antiperiplanar (app) and Gauche conformers

App and Gauche (of the centre 4 carbon atoms) 1,5-hexadiene was created using Gaussview 5.0. The structure was first roughly approximated using the "Clean" function in Gaussview (the default "Clean" function settings were used). Optimisation of the cleaned 1,5-hexadiene (app) is then done using the Hartree-Fock (HF) method and 3-21G basis set.

The HF method is a derivation of the Schrodinger equation and it approximates structures in Gaussview by solving the ground state wave function and energy. Although 1,5-hexadiene is not a large molecule but calculations takes considerably longer time as more atoms is added to a molecule. The basis set 3-21G was hence used to provide reasonable accuracy with quick calculations.

• Method: Hartree-Fock
• Basis set: 3-21G

Optimising a molecule in Gaussview means solving the Schrodinger equation to find the lowest energy structure, i.e. the structure with least electronic, nuclear repulsion and maximum electrostatic attraction. The Schrodinger equation involves solving the kinetic and potential energy part of the wave function of a molecule. By trial and error, Gaussview is able to find the minimum energy in the potential well (e.g. the Lennard-Jones potential). This also explains why larger molecules take considerably longer time to compute as the number of possible structures increase exponentially as number of atoms in a molecule increases.

After Gaussview finishes the calculation, The energy of the optimised 1,5-hexadiene can be assessed by opening the .log file in Gaussview and click "Summary" in the "Results" tab.

Below is an example of one of the optimised 1,5-hexadiene (C_i point group symmetry) with its Summary table.

1,5-hexadiene app optimisation summary
1,5-hexadiene APP

This sample item table was extracted from the raw .log file of 1,5-hexadiene (C_i) generated from Gaussview. It shows that the placement of the optimisation was converged, stationary point was found and the optimisation was successful. This procedure was done after each optimisation to ensure that the job is successfully executed. The other item tables will not be posted explicitly in order to keep the wiki page concise.

        Item               Value     Threshold  Converged?
Maximum Force            0.000060     0.000450     YES
RMS     Force            0.000010     0.000300     YES
Maximum Displacement     0.000464     0.001800     YES
RMS     Displacement     0.000171     0.001200     YES
Predicted change in Energy=-2.037161D-08
Optimization completed.

Other 9 conformers were also optimised and the below table is a summary of those conformers. The raw .log file can be accessed by clicking the link. In general, antiperiplanar conformation will have a lower energy than gauche conformation because there are less steric repulsion between adjacent groups. My guess for the lowest energy conformer would be 1,5-hexadiene with C_i point group symmetry because it's takes a zig-zag like structure and there's least steric repulsion.

Optimisation of 1,5-hexadiene

Conformer	Structure	Point Group	Energy (a.u.)	Reference Energy (a.u.)	Relative Energy(kcal mol-1)	raw .log file
Antiperiplanar (App) 1	app C1	C1	-231.69097048	-231.69097	2.25	File:APP C1.LOG
App 2	app C2	C2	-231.69260232	-231.69260	1.06	File:APP C2.LOG
App 3	app C2h	C2h	-231.68907057	-231.68907	0.08	File:APP C2h.LOG
app 4	app Ci	Ci	-231.69253528	-231.69254	0.04	File:App Ci.LOG
Gauche 1	Gauche_C1_1	C1	-231.69266113	-231.69266	0.00	File:GAUCHE C1 1.LOG
Gauche 2	Gauche_C1_2	C1	-231.68961575	-231.68962	1.91	File:GAUCHE C1 2.LOG
Gauche 3	Gauche_C1_3	C1	-231.68916020	-231.68916	2.20	File:GAUCHE C1 3.LOG
Gauche 4	Gauche_C2_1	C2	-231.69166702	-231.69167	0.62	File:GAUCHE C2 1.LOG
Gauche 5	Gauche_C2_3	C2	-231.69153033	-231.69153	0.71	File:GAUCHE C2 2.LOG
Gauche 6	Gauche_C2_3	C2	-231.689771615	-231.68772	3.10	File:GAUCHE C2 3.LOG

Lowest energy 1,5-hexadiene (HF, 3-21G)

Most of the energies calculated were indeed, as predicted, overall lower in the antiperiplanar conformation. However, the lowest energy conformation (-231.69266113 a.u.) was actually the 1,5-hexadiene with gauche conformation and C1 point group symmetry (as shown on the right hand side). This could be explained by the fact that steric repulsion forms only part of the Schrodinger equation, the orbital overlap integral in this conformer might be larger than the antiperiplanar conformer (due to less diffused MOs); Compromising both repulsion and attraction, leading to a overall energy lowest energy. Further investigation can be done by doing a population analysis and generating the MOs of this conformer.

The computed energies agree closely with the reference energy meaning that the conformations computed were the ones required. In the following section, we're going to use a higher level basis set and compare the final structure and energy.

Optimisation using DFT, B3LYP/6-31G

The method DFT, B3LYP combined with the basis set 6-31G is widely used nowadays as it provides a good accuracy in a reasonable time. In this section, we're going to pick a few of the lowest energy conformers to compare with the results computed using 3-21G basis set. It's worth pointing out that conformers can only be compared when the same method and basis set are used. Comparison of the energy in this case only shows that DFT, B3LYP is a higher level and more accurate method.

Optimisation using the DFT,B3LYP method and 6-31G basis set

Conformer	App 4	App 3	Gauche 1
Structure (Optimised with 6-31G)	1,5-hexadiene APP	1,5-hexadiene APP	Gauche_C1_1_631G
Point Group	Ci	C2h	C1
3-21G Energy (a.u.)	-231.69253528	-231.68907057	-231.69266113
6-31G Energy (a.u.)	-234.55970423	-234.55770073	-234.55933663
C-C Bond lengths (Å) 3-21G	1.509 / 1.553	1.514 / 1.535	1.509 / 1.553
C-C Bond lengths (Å) 6-31G	1.507 / 1.555	1.511 / 1.534	1.508 / 1.557
C=C Bond lengths (Å) 3-21G	1.316	1.317	1.316
C=C Bond lengths (Å) 6-31G	1.338	1.339	1.339
C-C-C-C dihedral angle (o) 3-21G	180.0	180.0	67.7
C-C-C-C dihedral angle (o) 6-31G	180.0	180.0	66.5
C=C-C-C dihedral angle (o) 3-21G	114.7	0.0	117.2
C=C-C-C dihedral angle (o) 6-31G	118.7	0.0	120.0
raw .log file of 6-31G	File:APP CI 631G.LOG	File:APP C2H 631G.LOG	File:GAUCHE C1 1 631G.LOG

The above table shows the comparison between energies, dihedral angles and bond lengths computed using different methods and basis sets. The energy shows that by using a higher level basis set, a more negative energy is obtained meaning that the basis set is a more sophisticated one and is closer to the real molecular structure in its ground state.

Although the C-C-C-C dihedral angle and C-C bond length didn't change much, however, there's a significant lengthening in C=C bond length and widening of C=C-C-C dihedral angle. From the above observation, we can say that the difference in energy might have come from different approach to calculate the C=C in 3-21G compared to 6-31G basis set. The longer C=C bond suggests that the π orbitals might be slightly more diffused or the repulsion between carbon atoms is greater when 6-31G basis set is used.

Frequency analysis of C_i conformer

Low frequencies ---   -9.6237   -0.0003    0.0009    0.0009    0.4914   12.2665
Low frequencies ---   71.8214   79.9299  116.7438

The above data is abstracted from the raw .log file frequency analysis. There are 6 "zero" low frequencies suggesting that there are 3N-6 vibrational motions. There are 6 carbons and 10 hydrogens in 1,5-hexadiene case suggesting that there are 42 (3N-6, where N=16) vibrational motions. Indeed, from the "Vibrations" under "Results" tab, 42 different vibrational motions were computed.

Another useful feature doing the frequency analysis is to confirm that the optimisation was successfully executed, where the second line of the "low freqencies", the "real frequencies" shows no negative values. Negative values indicates that the vibration is imaginary and either something has gone wrong with the optimisation or frequency analysis. In addition the "zero" frequencies (first line) are within +/- 15cm^-1 indicates the frequency analysis was done with reasonable accuracy. In short, the optimisation and the frequency analysis were successfully executed.

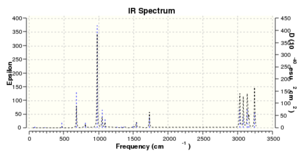
The generated IR spectrum is compared with an experimental IR spectrum, we can see that the computed spectrum assembles closely to the real IR spectrum, indicating the high accuracy and advantage of using computational chemistry.

Computed IR spectrum of 1,5-hexadiene (Ci conformer) (DFT, B3LYP, 6-31G)

Experimental IR spectrum of 1,5-hexadiene (Ci conformer)

Thermochemistry

Zero-point correction=                           0.143460 (Hartree/Particle)
Thermal correction to Energy=                    0.150751
Thermal correction to Enthalpy=                  0.151695
Thermal correction to Gibbs Free Energy=         0.111854
1. Sum of electronic and zero-point Energies=           -234.416244
2. Sum of electronic and thermal Energies=              -234.408953
3. Sum of electronic and thermal Enthalpies=            -234.408009
4. Sum of electronic and thermal Free Energies=         -234.447850

The above data was extracted from the raw .log file of the frequency analysis of C_i conformer.

• 1. Sum of electronic energy and the zero point energy, energy at 0K (E = E_elec + Zero Point Energy)
• 2. Energy at room temperature and atmospheric pressure, 298.15K and 1 atm, which includes the electronic energy and the three kinetic energies: Vibrational, rotational and translatioinal (E = E₀ + E_vib + E_rot + E_trans)
• 3. Sum of electronic and thermal enthalpies, useful when calculating dissociation energy (H = E₀ + RT)
• 4. Sum of electronic and free energies, which is the entropic part of the free energy, (G = H-TS)

"Chair" and "Boat" Transition Structures

As mentioned in the previous section, Cope rearrangement undergoes two possible transition states. In this section, we're going to use Gaussview to compute these TS using different methods. 3. QST2 method The chair TS has a symmetry point group of C_2h and the boat TS has C_2v

Chair TS optimisation

1. Optimisation using the "guess" method The chair TS was optimised by the following approach

• Optimising a allyl C₃H₅ fragments .log file
• Placing 2 fragments at a distance of around 2.2 Å apart for the terminal carbons
• Optimise using the following settings: HF / 3-21G; Opt+Freq; Optimization to TS (Berny); force constant: Once; Additional Keyword: Opt=NoEigen

The optimised .log file can be found here

guess1

Low frequencies --- -818.0568   -0.0007   -0.0005    0.0001    4.3559    5.2734
Low frequencies ---    6.8275  209.7212  395.9291
******    1 imaginary frequencies (negative Signs) ****** 

The imaginary vibration frequency at approx. -818cm^-1

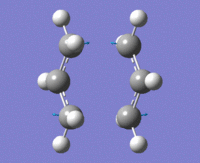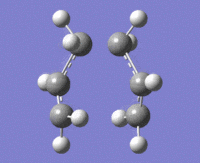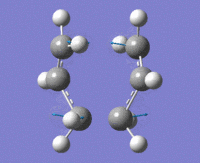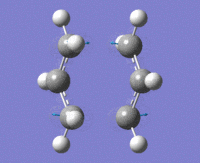
The above data was extracted from the .log file of the optimised "guess" method. It is confirmed that there's one imaginary frequency at approx. -818cm^-1

As we can see from the diagram on the right, one end of terminal carbon atoms from the imaginary vibration is moving towards each other, and the other end moving away, similar to the bond make/break motion of the Cope rearrangement.

2. Freeze coordinate method

This method involves two parts, the first part consists of freezing the terminal carbons in the allyl and optimising the other atoms to the minimum energy in both C₃H₅fragments and the second part involves unfreezing the frozen terminal carbons and optimising it to obtain the overall minimum energy.

• First Part: Set the terminal carbons as "Bond" and "Freeze coordinate" in "Redundant coordinate" in the Edit tab. Then optimise the molecule using HF/3-21G basis set. .log file

guess3

• Second Part: unfreeze the terminal carbon atoms and minimising their energy by setting the terminal carbons as "Bond" and "derivatives" under "Redundant coordinate". .log file

guess4

Bond Length and Angles of the optimised Chair TS

Method	Basis Set	Total energy (a.u.)	Distance between terminal Carbons (Å)	C=C Bond lengths (Å)	Bond angle within fragment (°)
Hartree Fock	3-21G	-231.61932247	2.02	1.39	120.50
Freeze Coordinate	3-21G	-231.61932157	2.02	1.39	120.51

From the above table, we can see that other than the total energy is very slightly lower using the hartree fock method, the other parameters virtually remain unchanged. Given that the basis set used is the same, this signifies that both Hartree Fock and Freeze Coordinate method are similar.

Boat TS optimisation

An alternative method was used to compute the Boat TS using the method QST2 (Synchronous Transit-Guided Quasi-Newton ) as opposed to the "guess" method. One of the advantages of using this method (QST2) is that it's fully automated and we don't have to guess the position and the distance between fragments before starting. Due to the nature of this method, the reactant and product are required as inputs and it automatically works backwards to simulate the transition structure. However, one of the downside of this approach would be the computer wouldn't automatically rotating the bond to make the conversion possible. Instead, we'll either have to use one of the gauche conformers or manually rotating the antiperiplanar C_i conformer such that the reactant and product geometry is closer to the transition state. An more reliable method, QST3 can also be used but it requires the initial structure of the transition state as well as reactant and product.

To make the QST2 method possible, we first have to relabel the optimised (HF / 3-21G) 1,5-hexadiene such that the computer recognize the change in geometry between reactant and product; enabling the TS state to be computed. The relabeled reactant and product are shown below.

Secondly, the dihedral angle of the centre 4 carbon atoms was set to 0^o followed by setting the central 3 carbon atoms to 100^o. This step is required to "guide" the computer to the the right direction, otherwise, the calculation could have gone for ages without finding a possible pathway to get from reactant or product to the transition structure, eventually terminating the calculation and shown as error. Fortunately for us, thanks to the guide in the lab script, we're able to compute the result without too much trouble. The result .log file can be accessed here

Relabeling of the reactant, 1,5-hexadiene (Ci conformer)

Relabeling of the product, 1,5-hexadiene (Ci conformer)

The animation of the imaginary vibrational motion at approx. -840 cm-1 Please click the image for animation

Low frequencies --- -839.9914   -7.4236   -7.1658   -2.0292   -0.0007   -0.0005
Low frequencies ---    0.0002  155.0920  382.2380
******    1 imaginary frequencies (negative Signs) ****** 

The .log file extracted from the computed shows that there's only 1 imaginary frequency and its motion is shown above.

boat_ts_qst2

The above jmol shows the boat transition state of the Cope rearrangement of 1,5-hexdiene

• Method: QST2
• Basis set: 3-21G

Bond Length and Angles of the Boat TS

Energy (a.u.)	Distance between terminal Carbons	C=C Bond lengths	Bond angle of within fragment
-231.60280239	2.14 Å	1.38 Å	121.67°

Boat TS has an energy of -231.60280239 a.u. whilst the Chair TS has approx. -231.61932200. It make sense that the Chair TS has a lower overall energy due to less steric repulsion between both allyl fragments. This is confirmed by the higher distance between terminal carbons, (2.14 Å in boat v.s. 2.02 Å in chair).

Similar to cyclohexane, the chair conformer is more stable than the boat conformer. On a side note, since cylohexane exist as half chair conformation and twisted boat as well, half chair TS and twisted boat TS might also exist in the 1,5-hexadiene Cope rearrangement. My guess is that half chair TS and twisted boat TS are actually part of the transition of the chair / boat TS therefore they might not be as well defined as the half chair and twisted boat in cyclohexane.

Intrinsic Reaction Coordinate

Simply by observing the vibrational motion of the TS, it's hard to tell which conformer is actually forming. The intrinsic reaction coordinate (IRC) is useful in this case in a sense that it changes the geometry of the reactant or product (depending on settings) little by little in the direction of lower energy until a minima is found which corresponds to either the reactant or product.

IRC can be computed by opening the .chk file and choosing "IRC" under the Job type. There are a few options we can choose,

• 1. Compute the forward, backward reaction or both
• 2. Calculate the force constant once or always (in order to verify that the optimised geometry is a transition state)
• 3. Number of points along IRC

1. Since reactant and product is symmetricial in the Cope rearragement, therefore it's sufficient to compute only the forward reaction. However, in the following I'll compute both directions for both transition structure since it gives the whole picture of the rearrangement.

2. Although force constant can be calculated once only but it's more reliable to calculate it each step. Further more, the molecule we're trying to compute is not excessively large therefore the time it takes to complete the calculation will hopefully not be too long.

3. Although more time will be needed for this single calculation, but in order to avoid having to repeat the calculation, 100 points along IRC was computed.

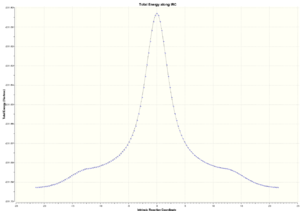
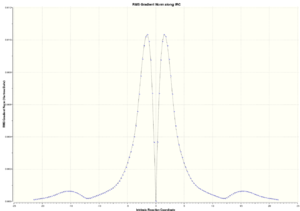
Chair IRC

100 number of points along IRC and both directions of the Cope rearrangement were computed. As we can see from the total energy plot, the maximum represents the chair transition structure and the bottom of the curve represents the reactant or product. The RMS gradient plot represents the change in gradient of total energy; there's a drop in the middle of the curve where the change in gradient is zero representing the transition structure.

The .log file can be accessed here

The IRC of the chair TS of 1,5-hexadiene in animation (HF, 3-21G)

The total energy plot from the reactant to the chair transition structure

Root mean square gradient for the IRC of the chair TS

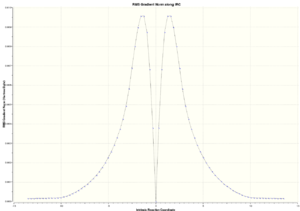Boat IRC

The same as the Chair IRC, 100 number of points along IRC and both directions of the Cope rearrangement were computed. The total energy plot of the boat IRC is more interesting as it shows that the energy goes through a point of inflection and this can be clearly seen in the RMS gradient plot, where the change in gradient goes near zero. My guess for this occurrence is that, similar to the twist boat in cyclohexane, the structure undergoes an intermediate energy minimum when going through from the reactant to the transition state.

The .log file can be accessed here

The IRC of the boat TS of 1,5-hexadiene in animation (HF, 3-21G)

The total energy plot from the reactant to the boat transition structure

Root mean square gradient for the IRC of the boat TS

Activation energy of 1,5-hexadiene Cope rearrangement

To obtain a better accuracy of the thermodynamic data, higher level basis set (B3LYP / 6-31G) was used to reoptimise the chair and boat transition structures. The activation energy is calculated by taking the difference between the energy of the reactant and the energy of the transition state.

Reoptimised Chair TS			Reoptimised Boat TS
Chair Reopt			Boat Reopt
	HF / 3-21G	B3LYP / 6-31G		QST2 / 3-21G	B3LYP / 6-31G
Energy (a.u.)	-231.61932157	-234.50546654	Energy (a.u.)	-231.60280239	-234.49291522
Distance between terminal carbons (Å)	2.02	2.03	Distance between terminal carbons (Å)	2.14	2.26
C=C bond length (Å)	1.39	1.41	C=C bond length (Å)	1.38	1.40
Bond angle within fragment (°)	120.50	120.96	Bond angle within fragment (°)	121.67	122.87

From the above table, when using a higher level of basis set, the energy is lower. Once again, we cannot directly compare the results when using different basis sets, but what we can see from the above data is that the distance between terminal carbons, the bond length and the angle within the fragment are quite similar, indicating that in terms of geometry, HF / 3-21G gives a similar result to B3LYP / 6-31G but the parameters used to compute the energy is very different.

Below are the thermochemistry data extracted from the .log file after reoptimisation.

Chair TS

Sum of electronic and zero-point Energies=           -234.362689
Sum of electronic and thermal Energies=              -234.356773

Boat TS

Sum of electronic and zero-point Energies=           -234.351364
Sum of electronic and thermal Energies=              -234.345059

The log files can be accessed below

Chair Reoptimisation .log

Boat Reoptimisation .log

Before calculating the activation energy, we have to know the energy of the reactant. There are two approaches, as follow:

Identify, from IRC, which of conformers the reactant is most likely to have assembled from. This can be done by comparing the reactant (or product, since it's symmetrical) with the range of conformers computed previously. After knowing which conformer assembles the transition structures by visual inspection, reoptimisation is need to be performed (DFT, B3LYP / 6-31G) to ensure the methods and basis set used are the same for data to be comparable. Lastly, frequency analysis is performed to obtain the thermochemistry data for comparison.

• 1. Visual identify
• 2. Reoptimisation using B3LYP / 6-31G
• 3. Frequency analysis

Alternatively, we can take the reactant structure out from the IRC, reoptimising it and perform frequency analysis to compare the energies. This seems to be the better method (and will be used) as it eliminates the risk of visually identifying the wrong conformer.

The Chair TS most like came from Gauche 4, the conformer with relative energy 0.62 kcal/mol.

Gauche 4(HF/3-21G)

Reactant of the chair TS from IRC

And for the Boat TS, most like came from Gauche 1, the conformer with relative energy 0.00 kcal/mol.

Gauche 1(HF/3-21G)

Reactant of the Boat TS from IRC

Activation energies

	0K			298.15K
Structure	Activation Energy (a.u.)	Activation Energy (kcal/mol)	Experimental (kcal/mol)	Activation Energy (a.u.)	Activation Energy (kcal/mol)	Experimental (kcal/mol)
Chair TS	0.000433	0.272	34.06	0.000516	0.324	33.17
Boat TS	0.64381	403.7	41.96	0.63513	398.3	41.32

From the above table, we can see that the computed activation energy deviates strongly from the experimental data. This has suggested that taking the structure calculated from 3-21G basis set and optimising using 6-31G might not be a good pathway to obtain the activation energy in this case. Further work can be done by using solely the 3-21G basis set to obtain the energy of the reactant and the transition state to recalculate the activation energy.

Reoptimised reactant of the chair TS (Structure taken from the IRC for reoptimisation)

Sum of electronic and zero-point Energies=           -234.415312
Sum of electronic and thermal Energies=              -234.408056

Reoptimised reactant of the boat TS (Structure taken from the IRC for reoptimisation)

Sum of electronic and zero-point Energies=           -234.415745
Sum of electronic and thermal Energies=              -234.408572

Diels-Alder Cycloaddition

Introduction

Hückel topology, suprafacial stereospecific prodcut

Diels-Alder reaction is a type of cycloaddition where a conjugated diene (e.g. cyclopentadiene, butadiene) and a dienophile (e.g. ethylene, cyclohexenone) react through a concerted cyclic fashion to create a six-membered ring with one C=C bond.

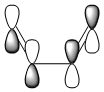
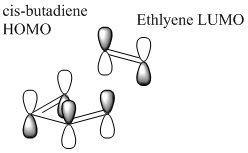
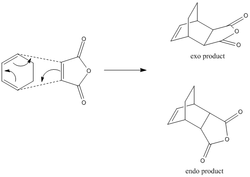
A typical Diels-Alder reaction involves 4π electrons from the diene and 2π electrons from the dienophile, breaking 3π bonds and creating 2 new σ bonds. The reaction is stereospecfic and in general, thermally controlled; there are 6 electrons (4n+2, where n=1) involved. This signifies that the pericyclic reaction goes according to Hückel suprafacial topology, resulting in stereospecific product, as shown on the right.

There are two Diels-Alder reaction we're going to consider in this second half of the course. First, the reaction between cis-butadiene and ethlyene (shown in the bottom left diagram) where cis-butadiene is the diene and ethylene is the dienophile. It is important that butadiene is on its cis-conformation as the reaction will not proceed with trans-butadiene (no concerted cycloaddition possible). In this reaction, having Hückel or Möbius topology don't make a difference because all atoms attached are identical hydrogen.

The reaction between cyclohexa-1,3-diene (diene) and maleic anhydride (dienophile) is concerned in the second reaction. Since the substituents on the carbon atoms are different, one must to consider whether the end product is an exo or an endo one. Second-orbital overlap (SOO) plays an important role in determining the major product in this reaction.

reaction scheme of cis-butadiene and ethlyene

Reaction scheme cyclohexa-1,3-diene and maleic anhydride

Reaction of cis-butadiene with ethylene

cis-butadiene and ethylene were drawn and optimised using the following method:

• Method: Semi-Emperical
• Basis Set: AM1

butadiene log Ethylene log

Optimisation using B3LYP, 6-31G was also attempted and it has been found although the geometries looked similar but there's a large difference in energy (e.g. 0.02619024 a.u. v.s. -78.57203626 a.u. for ethylene). The fact that cis-butadiene and ethlyene have positive total energy when using AM1 basis set means that AM1 is a low level basis set, as we know that cis-butadiene and ethlyene does exist in nature in its pure form as gases.

butadiene B3LYP 6-31G log ethlyene B3LYP 6-31G log

MO analysis of cis-butadiene and ethlyene

The HOMO and LUMO of the two molecules are tabulated below. The MOs are important piece of information as it shows whether the reaction between is allowed or forbidden. Only MO with the same symmetry are allowed to react. From the below LCAO or the computed MO, we can predict that cis-butadiene LUMO is allowed to react with ethlyene's HOMO and cis-butadiene HOMO is allowed to react with ethylene LUMO. Although the MOs are allowed interact but whether they will interact or not depends on the energy of these MOs. If the energy gap between MOs are too large and the mixing result in overall increase in energy, the interaction will not happen. On a side note, we can see that the LUAOs resemble closely to the computed MOs showing that the LCAO is a very powerful method of representing the real molecular orbitals.

Frontier orbitals of cis-butadiene and ethlyene

MO	LCAO	Visualised MO	MO symmetry wrt plane	MO symmetry wrt perpendicular plane	Energy (au)
cis-butadiene HOMO			Anti symmetric	Anti symmetric	-0.34382
cis-butadiene LUMO			Anti symmetric	Symmetric	0.01709
Ethlyene HOMO			Anti symmetric	Symmetric	-0.38777
Ethlyene LUMO			Anti symmetric	Anti-symmetric	0.05284

Below shows the MO diagram together with the computed MOs.

For Butadiene, the HOMO and LUMO are determined by the number of nodes perpendicular to the plane of molecule. Ψ₂, or HOMO, consist of 1 node in the middle and has a negative energy; Ψ₃, or LUMO consist of 2 nodes and has a positive energy.

MO diagram of cis-butadiene

MO diagram of ethylene

Transition state of the reaction of cis-butadiene and ethlyene

The transition state of this Diels-Alder reaction involves an envelope type structure, as the hydrogens attahed are identicial, the exo and endo products are also identical.

The molecule bicyclo[2,2,2]octane was used as a template and the CH₂-CH₂ group was removed to create the transition structure for the optimisation. The frozen coordinate method was used, and the distance between the terminal carbons was set to be 2.2Å ( literature: 2.27Å ) and optimisation was done using the following settings:

• Job Type: Opt+Freq, TS (Berny), Calculate Force Constant: Once, Additional Keyword: opt=noeigen
• Method: Semi-Empeirical
• Basis set: AM1

Imaginary frequency of the TS at -956.3220cm^-1

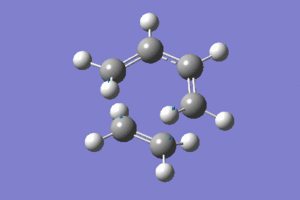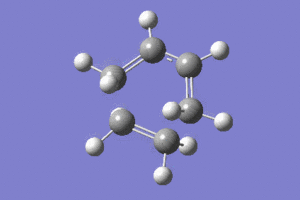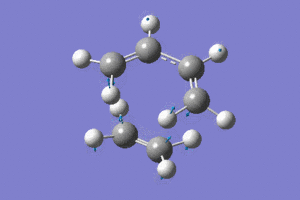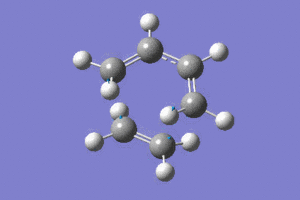
Chair Reopt

The .log file for the first step can be found here

The final energy computed for the transition state for the was 0.11165468 a.u. and the .log file can be found here

As expected, one large imaginary frequency was found at -956.3220cm^-1 and its animation is shown on the right.

Low frequencies --- -956.3220   -2.3477   -0.0681   -0.0033    0.0090    2.0249
Low frequencies ---    2.6871  147.0434  246.6198
******    1 imaginary frequencies (negative Signs) ******

Bond lengths of cis-butadiene and Ethylene, their TS and comparison of different methods

	cis-butadiene (AM1)	cis-butadiene (6-31G)	Ethylene (AM1)	Ethylene (6-31G)	cis-butadiene TS (AM1)	cis-butadiene TS (6-31G)	Ethylene TS	Ethylene TS (6-31G)
C=C (Å)	1.33	1.34	1.34	1.34	1.38	1.39	1.38	1.39
C-C (Å)	1.45	1.47	n/a	n/a	1.40	1.40	n/a	n/a
C-H (Å)	1.10	1.09	1.09	1.09	1.09	1.09	1.09	1.09
Bond Angle (o)	125.7	127.2	n/a	n/a	121.2	122.0	n/a	n/a

The above table shows the difference in bond lengths when computing cis-butadiene, ethlyene and their transition state using Semi-empirical AM1 and B3LYP 6-31G. The log files can be found below:

Butadiene and Ethlyene AM1 & 6-31G

TS AM1

TS 6-31G

As we can see from the above table, as we move from the reactant to the transition structure, bond angle within the cis-butadiene decreases, C-C bond length decreases, C=C bond length increases and C-H bond length remained constant.

• Bond angle of butadiene decreases: as the reactant move towards the transition state, σ-bond and a 6 membered ring is partially formed between the terminal carbon atoms and ethlyene. As 6 membered ring is more strained than a free cis-butadiene therefore the bond angle is decreased.
• C-C bond length decreases: the product of the Diels-Alder reaction between cis-butadiene and ethlyene is a cyclohexene and it's the C-C bond in the cis-butadiene that's turning in the C=C bond. As bond order increase, the bond length decreases, hence the observed phenomenon.
• C=C bond length: this is the exact opposite of the above phenomenon, in the transition state, the C=C bond order in cis-butadiene decreases due to the population of the antibonding orbital and the partially formation of σ-bond, causing the bond to weaken and lengthen. This can be clearly seen from the IRC animation, where the C=C weaken and turning into a C-C bond and the terminal carbons are transformed from sp² hybridised to sp³ hybridised.
• C-H bond length: remains constant as expected because C-H bond is not involved in the reaction

The average bond length for a C-C sp²–sp² is 1.47 Å, 1.34 Å for C=C and 1.09 Å for sp² C-H. From the above table, the 6-31G basis set shows a better agreement with the literature, although the difference is only 0.01 Å. This again, highlights that the 6-31G basis set shows a higher accuracy than AM1. On the other hand, the 6-31G basis set took a significantly longer time to compute as we'll soon find out from the IRC analysis using 6-31G basis set.

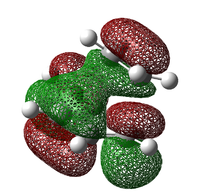
MO analysis

The HOMO of the TS of the reaction between cis-butadiene and ethlyene	The LUMO of the TS of the reaction between cis-butadiene and ethlyene
The LCAO of the HOMO of the TS of the reaction between cis-butadiene and ethlyene	The LCAO of the LUMO of the TS of the reaction between cis-butadiene and ethlyene

From the above computed MOs of the TS, we can see the electron distribution map of the transition state - just before the formation of σ-bonds. Once again, the LCAO shows a close agreement with the computed MOs and points out the fact that orbitals must have the same symmetry for interactions to be allowed.

The MO diagram showing the HOMO LUMO interaction between cis-butadiene and Ethylene

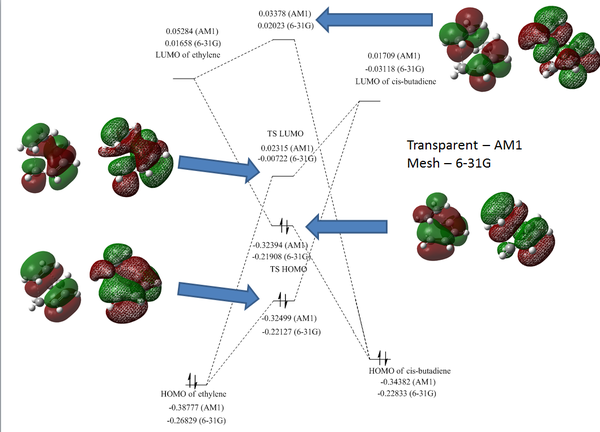
The MO diagram above shows a rather complicated interaction between the HOMO and LUMO interaction of cis-butadiene and ethylene but nevertheless, the energy of the transition state is clearly above both cis-butadiene and ethlyene. The energy plot will be available in the next section showing the energy profile from the reactant to the product.

The mesh MOs represents MO computed using 6-31G basis set and the transparent represents AM1, it's interesting that the HOMO-1 and the HOMO MOs are swapped when different basis sets are used. Moreover, contribution form hydrogen can also be seen when 6-31G is used meaning that the real MO might consists of non π orbital contribution, where the AO of hydrogen is also part of the full MO - something that LCAO didn't account for.

Comparison of HOMO & LUMO energies of different methods

	cis-butadiene (AM1) (a.u.)	cis-butadiene (6-31G) (a.u.)	Ethylene (AM1) (a.u.)	Ethylene (6-31G) (a.u.)
HOMO	-0.34382	-0.22833	-0.38777	-0.26829
LUMO	0.01709	-0.03118	0.05284	0.01658

The above table shows that the calculated energies are different when different basis sets are used. Although knowing that 6-31G basis set is a higher level one, however, the LUMO of cis-butadiene actually turned out to be negative, suggesting that cis-butadiene can be a potential electron acceptor. If we turn our attention back to the LUMO in the MO diagram above, the difference in calculated energy between AM1 and 6-31G basis sets seemed to have come from the σ-orbital contribution from hydrogen. This might explain why the LUMO energy seems to be negative. In addition, it also points out that the LCAO method is better in replicating the AM1 basis set.

IRC analysis

The formation of the σ bond was computed using the IRC option in Gaussview and two different basis sets were used: AM1 and 6-31G.

Both basis sets were run in both directions, force constant always and 100 points were computed. The result .log file can be found here: AM1 6-31G

From the CPU run time alone, we can see that the 6-31G is a much higher level basis set than AM1; the time taken to run the IRC using AM1 was approx. 5 mins, whilst using 6-31G took a staggering 5.5 hours!! The total energy graph and the energy gradient RMS looked pretty much identical however.

Due to the way Gaussian work, unfortunately, the IRC animation is the other way round, showing the product going through the transition state and back to the higher energy reactant.

The IRC showing the Diels-Alder reaction between Butadiene and Ethlyene (AM1)

The IRC showing the Diels-Alder reaction between Butadiene and Ethlyene (6-31G)

The IRC showing the Diels-Alder reaction between Butadiene and Ethlyene (AM1)

The IRC showing the Diels-Alder reaction between Butadiene and Ethlyene (6-31G)

The IRC showing the Diels-Alder reaction between Butadiene and Ethlyene (AM1)

The IRC showing the Diels-Alder reaction between Butadiene and Ethlyene (6-31G)

Reaction of cyclohexa-1,3-diene with maleic anhydride

The exo and endo products of cyclohexa-1,3-diene with maleic anhydride

The reaction between cyclohexadiene and maleic anhydride is different to the reaction between cis-butadiene and ethlyene since the substituents on the carbons are different.

Maleic anhydride in this reaction is the dienophile, it is electron deficient due to the electron-withdrawing effect of oxygen. Due to Secondary orbital overlap effect, the transition state is stabilised by a secondary pi-orbital overlap, lowering the total energy of the transition state, leading to the fast, kinetic product (endo). Therefore the major product is the endo product. On the other hand, the thermodynamic product is the exo form. We shall explore this theory quantitatively, by computing the transition states and obtain the energies for confirmation.

• Job Type: Opt+Freq
• DFT / B3LYP, 6-31G

	Cyclo-1,3-hexadiene	Maleic Anhydride
jmol	CD	MA
Total energy (a.u.)	-233.41891079	-379.28954441
.log file	cyclohexadiene.log	Maleic Anhydride.log

HOMO & LUMO energy of the reactants

	Cyclo-1,3-hexadiene (6-31G) (a.u.)	MO plot	Symmetry wrt plane of molecule	Symmetry perpendicular to plane of molecule	Maleic Anhydride (6-31G) (a.u.)	MO plot	Symmetry wrt plane of molecule	Symmetry perpendicular to plane of molecule
HOMO	-0.20872		Anti-symmetric	Anti-symmetric	-0.29927		Symmetric	Anti-symmetric
LUMO	-0.01496		Anti-symmetric	Symmetric	-0.11713		Anti-symmetric	Anti-symmetric

From the table above, we can work out whether the symmetry of the LUMO and HOMO matches and the reaction is allowed or not. We can then work out the energy difference between HOMOs and LUMOs and predict whether cyclohexadiene's HOMO will react with maleic anhydride's LUMO or the other way round.

• Cyclohexadiene LUMO + maleic anhydride HOMO: energy difference = 0.28431 a.u. = 178.4 kcal/mol
• Cyclohexadiene HOMO + maleic anhydride LUMO: energy difference = 0.09159 a.u. = 57.5 kcal/mol

The calculated energy difference shows that the HOMO of cyclohexadiene is likely to react with LUMO of maleic anhydride due to smaller energy difference. It's interesting that both molecules have negative energies in their LUMO indicating that the equilibrium lies on the product side of the diels-alder cycloaddition. However, whether the molecules are allowed to react or not depend on another important factor, symmetry. The fact that the cyclohexadiene HOMO matches the maleic anhyride LUMO symmetry, we now can quite safely say it's the cyclohexadiene HOMO that will react with the LUMO of maleic anhydride and the concerted cycloaddition is favourable. We shall confirm this in the next section by computing the MOs of the transition state.

exo and endo transition states

The freezing coordinate method was used because the diels alder reaction between maleic anhydride and cyclohexadiene is well known and a reasonable guess of the position of the two compounds can be made. Both the exo and endo transition structures were computed using DFT/B3LYP, 6-31G methods and basis set because it compromises both time needed to compute and accuracy. In addition, this was the method used to optimise maleic anhydride and cyclohexadiene previously and therefore consistency can be kept.

The result .log & .chk file can be found below

Exo product.log Exo product.chk

The Exo product with its major bond length is shown on the right:	guess1	guess1
The Endo product with its major bond length is shown on the right:	guess1	guess1

The total energy of the exo and endo product is listed below:

exo -612.563959666 a.u.

endo -612.56577194 a.u.

difference: 0.001812274 a.u. = 1.14 kcal/mol

As we could see from the above jmol of the products, most of the bond length in the exo and endo form are identical. The only difference is the distance between the carbon on the carbonyl of maleic anhydride & the nearest hydrogen on the cyclohexadiene; where in the exo form is 2.64Å and in the endo form, it's 3.51Å, the below diagram illustrate the through space distance with the carbon and hydrogen highlighted. The slightly more strained structure might explained the reason for a higher energy of the exo-form.

Exo-form product

Endo-form product

Activation energy

Exo and endo for activation energies calculation

	Exo	Endo
Sum of total energy of cyclohexadiene and maleic anhydride at 298.15K (a.u.)	-612.519391	-612.519391
Sum of electronic and thermal energies for the transition states (a.u.)	-612.367692	-612.370003
Activation Energy (a.u.)	0.151699	0.149388
Activation Energy (kcal/mol)	95.194	93.744

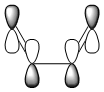
The exo transition state form shows a higher activation energy, which agrees with the finding that the endo-form is the kinetic product and exo form is the thermodynamic product. In other words, the endo-form is the faster product. As mentioned before, the secondary orbital overlap effect plays a important role in stabilising the transition state, leading to a lowering in the energy barrier. The LCAO of the secondary orbital overlap effect is shown in the below diagram:

the LCAO showing the interaction between the primary and secondary overlap interaction

The HOMO of the exo-form (6-31G)

The HOMO of the endo-form (6-31G)

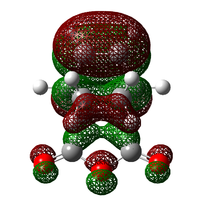Conclusion

This computational lab course has introduced us to compute the transition state of reactions, in particular, the cope rearrangement and the Diels-Alder cycloaddition. It has provided us a complete alternative to experimental chemistry with both accuracy and time-efficiency. We've tried using different method and basis sets such as AM1, B3LYP/6-31G and saw the difference it made to the energy and geometry of the molecules.

The Cope rearrangement involves a [3,3] sigmatropic rearrangement of 1,5 diene and undergoes boat or chair transition states. It has been confirmed that the chair conformation has a lower energy. The Diels-Alder cycloaddition involves a concerted cyclic reaction where 4π electrons from the diene and 2π electrons from the dienophile, total 3π bonds are broken and 2 new σ bonds are created. We've compute the reaction of cis-butadiene with ethylene and looked at how the bond length changes as the reaction proceeds in the first part of Diels-Alder cycloaddition section; and the reaction of cyclohexa-1,3-diene with maleic anhydride where there are two possible products, the exo and endo form, due to Secondary Orbital Overlap effect (SOO) the endo form is the kinetic, faster transition state with lower activation energy and hence is the dominating product.

Although some of the calculations didn't work straight away and some took a considerable amount of time to compute, but overall, I enjoyed the course, in particular the IRC part where we could really see the molecules in action and the sense of achievement that we now could compute a reaction during our own time and see all the interesting bits and pieces going on in a reaction in animation.