Rep:Mod:hj1213
Introduction
In this computational lab the Thermal properties, Free energy, DOS function and the phonon dispersion of Magnesium oxide was studied using primarily classical theory and to a lesser externt quantum mechanics. Both the size of the grid and the temperature was varied allowing the dependence of the value for the lattice parameter of MgO to be determined which in turn allowed the thermal expansion coefficient to be calculated.
Magnesium oxide (MgO) takes up a chrystal structure of Face-centered cubic (FCC) much the same as the Halite structure of Sodium chloride and consists of a lattice of doubly oxidized Mg2+ ions which cap each corner and face of the FCC lattice leaving the oxygen atoms in the center and at the edges.
The applications of MgO include Thermal and electrical insulation for wires, Fire retardant and medication for the relief of heart burn. Many of these applications owe there suitability to the thermal properties which can be predicted computationally.
Phonon dispersion
Phonons are discrete entities of vibrational energy which can be exited by thermal energy. Phonons exist in two branches, the optical, higher energy branch and the vibrational branch each exists at lower frequency vibrations.
The phonon desperation graph of MgO is shown above. This Graph shows the relationship between Vibrational frequencies of the phonon against K values in reciprocal space. In turn vibrational frequency can be converted to energy using the equation
This allows energies of individual phonon states to be assigned.
On the phonon dispersion graph there are six phonons for every value of K, as can be seen from the six lines on the graph. However for all symmetry points shown there is at least 2 degenerate phonons, as can be seen from the crossing lines resulting in the actual number of phonon states available at a given energy being less than 6. For Γ (k=0,0,0) there are 2 sets of doubly degenerate phonons with one tending to 0cm-1 (0 energy) and the other at around 400cm-1. The 2 phonon’s tending to 0 can be seen as in the acoustic region therefore as there is no vibration these modes must be associated with purely translational motion.
Phonon DOS
The density of states is the number of accessible vibrational states per energy interval. Graphically this can be represented by plotting the number of states per K value (obtained from the phonon dispersion graph) against the Vibration frequency. A grater number of K points sampled for the DOS calculation will result in a more accurate calculation. Large values of k will however be computationally tasking due to the large data sample therefore each calculation will be a compromise between computational workload and the accuracy of a result needed.

The (1x1x1) grid is associated with the L point on the Phonon dispersion graph. This is evident as the (1x1x1) DOS graph has 4 peaks which are associated with 4 separate phonon energy states. As there are six phonon lines in the dispersion relation this means that two sets of the phonons must be degenerate. Furthermore the intensity of the lower 2 peaks being double that of the higher 2 on the DOS graph indicate that the degenerate sets of phonons are the lower energy pairs. This means that the (1x1x1) grid must have 2 lower energy, acoustic, degenerate bands and 2 higher energy none degenerate, optical, bands which corresponds to the symmetry point L. The (1x1x1) grid however proved limited in the estimation of the MgO phonon description due to the small number of states.
Higher order grids were then used, (2x2x2), (4x4x4), (8x8x8), (16x16x16), (32x32x32), to attempt to calculate the optimum grid size for the approximation of the MgO DOS. It was noted that in the ranges studied that as the grid sizes increased the intensity of the peaks decreased, generally by a grater factor than the factor of increasing grid sizing. It was also noted that more peaks were evident in the higher order grids than in the lower. At higher wave numbers it became obvious that increasing the grid size also resulted in a ‘smoothening’ of the function graph. This can be rationalized by a grater number of sampling points.
From left to right (2x2x2), (4x4x4), (8x8x8), (16x16x16), (32x32x32)
For a minimum approximation for the density of states a smooth function, with fewVan Hove singularity’s should be obtained with no abrupt drops in the function to zero. As can be seen from the diagrams the lower grid sizes, bellow the 8th order grid, show drops in the DOS to zero at many points therefore are unsuitable approximations for the DOS. The (8x8x8) grid still contains many Van Hove singularity’s despite having no drops to zero this makes it inappropriate. The (16x16x16) grid is relatively smooth with no abrupt drops in the DOS to 0 therefore is a suitable approximation. It should be noted that the (32x32x32) grid appears even more suitable however is much more computationally expensive. Therefore the (16x16x16) grid was chosen as the most suitable approximation.
With regards to the structure of the DOS diagrams bellow the 4th order grid there is no obvious structure to the density of states. Above this grid a structure begins to appear with the lower energy acoustic states being more populated than the higher frequency optical states as can be seen from the higher DOS bellow 400cm-1 than above this value. An obvious peak begins to appear centered at around 400cm-1, growing wider between the 2nd order and the 8th order peaks before remaining a constant width between the (16x16x16) and (32x32x32) grid.
Free Energy
In this exercise the quasi-harmonic approximation aproximation was used to estimate the free energy of the MgO system. This approximation relies on the summing of all vibrational modes over the entirety of an infinite MgO chrystal.
The same grid sizes were used as in the phonon calculations. It was seen that the Helmholtz free energy converged with increasing grid sizes to around -40.9265eV. for the 4x4x4 grid there was a very small change in free energy with increasing grid size. If the (32x32x32) grid is taken to be the true accurate value for the Helmholtz energy then the precision of the calculation for varying grid sizes is given bellow.
The 1x1x1 can be seen to be a relatively large overestimate of the negativity of the calculated free energy as can the 2x2x2 grid to a lesser extent with a negative overestimate of 0.1meV. In the 4x4x4 and the 8x8x8 grid there is a slight positive overestimate of the value of the converged free energy. It can therefore be seen that the free energy can accurately be predicted by the 4x4x4 grid. The 1x1x1 grid was found to be in a precision range of 1meV, the 2x2x2 grid was found to be in the range of 0.5meV and the 4x4x4 grid was in a range of 0.1meV.
The initial increase in free energies with grid size can be rationalized by the idea that the free energy is made up from contributions from all of the phonons and a contribution from the interatomic pair potential. It is therefore logical that with increasing grid size the number of vibrational modes sampled was grater thus resulting in a larger value for the free energy. As with changing grid size the size of the cell remained constant at higher grid sizes the system could not access more vibrational modes as it could at lower grid sizes. This therefore led to the convergence of the free energy at higher grid sizes.
As Mgo and CaO both have the same FCC chrystal structure it is likely that the 4x4x4 grid, used for MgO, will be suitable for the for CaO. A small difference will arise as the unit cell of CaO is larger than that of MgO (4.82A)(1) which therefore results in the reciprocal cell being smaller. The reciprocal cell will therefore result in a more detailed DOS plot.
The size of the unit cell for Faujasite (24.7A) is much larger than MgO resulting in the unit cell in reciprocal space being 1/6th of the size of the MgO cell(2). This results in a grid 6 times smaller than the MgO grid to be used. The (1x1x1) grid will therefore be suitable for this compound.
Lithium adopts a body centered cubic crystal structure with a lattice constant of 3.490A(3). this make the unit cell slightly smaller than theta of MgO. Therefore the unit cell in reciprocal space will be larger for an equal density of K values. Therefore a larger grid should be used of at least the (8x8x8) grid should be used.
The thermal expansion of MgO
When MgO is heated it undergoes thermal expansion. This phenomena arises as an increase in temperature results in an increase in atom vibrations in turn results in the mean spacing between atoms to increase to avoid atomic collisions during vibrations. This not only results in increased atomic spacing but also changes the primitive cells motif. The thermal expansion of a chrystal is a phenomena which would not be predicted with classical, harmonic approximations of a solid as in this approximation the mean bond lengths across the atom stay constant with temperature.
The extent in which a given material thermally expands is given by the thermal expansion coefficient (α) and is expressed by the formula:
The free energy temperature dependance graph demonstrates a decreasing relationship between free energy and temperature. as the temperature increases further the gradient at which the function becomes more negative also increases.
This relationship is constant with the formula for the free energy 𝑓=−𝑘𝐵𝑇𝑙𝑛(𝑄)=0.5ħ𝜔+𝑘𝐵𝑇𝑙𝑛[1−𝑒^(-ħ𝜔/𝑘𝐵𝑇) ]. it can be seen that the logarithmic term in the expression dominates the relationship over the linear term hence the logarithmic appearance of the graph.
Above 400K the lattice vector was seen to increase linearly with temperature. Bellow 200K there was a constant relationship between temperature and lattice vector. This means that bellow 400K the model is inappropriate for modelling the lattice vector.
In this model it is assumed that the helmholtz free energy of every vibration is given by the formula 𝑓=0.5ħ𝜔+𝑘𝐵𝑇𝑙𝑛[1−𝑒^(-ħ𝜔/𝑘𝐵𝑇) ] therefore the total energy of the lattice is made up of the the sum of this formula over the entire lattice. It is also assumed that the energy of the entire system is a contribution from the vibrational modes and the potential between the individual atoms. the interatomic potential is modelled by the Leonard johnes potential. therefore the total energy is given by:
where the Ev us the vibrational energy and Ea is the interatomic energy.
When the QHA system was set up at high temperatures, close to the melting point of MgO, a large amount of atomic displacement was observed from the equilibrium positions. displacements were seen to be of such an amplitude that atoms may oscillate in to an adjacent unit cell. This is unlikely to happen due to the high energy of a system in which this occurs. therefore it can be concluded that at high temperature, close to the melting point of MgO, the QHA model is unsuitable for the modelling the system.
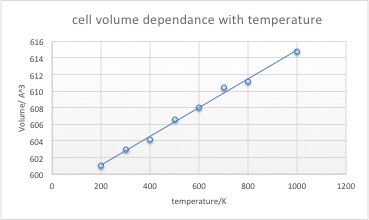
MD calculations yield a linear relationship between temperature and lattice volume.
When both QHA and MD methods are used to calculate the expansion coefficient a difference in results arises due to the different methods each calculation uses to generate a result. The molecular dynamics calculation uses potential energy surfaces in a classical mechanical approach whereas the QHA uses a model of Vibrating atoms which is mathematically describes as a harmonic function.
References
(1) C.H. Shen, R.S. Liu, J.G. Lin, and C.Y. Huang, Materials Research Bulletin, 2001, 36, 1139. (2)http://www.personal.utulsa.edu/~geoffrey-price/zeolite/fau.htm (3)R. S. Wei, August 1985, Volume 37, Issue 4, pp 191-203 , T. K. Gaylord