Rep:Mod:hgmd3

Module 3

by Hayleigh Gascoigne

Computational chemistry was used in this module to find transition states for reactions. This was dome using various methods, such as TS (Berny), frozen co ordinates and QST2. These transitions states were confirmed by the presence of one imaginary frequency in the frequency analysis.

The Cope Rearrangement

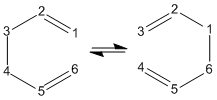
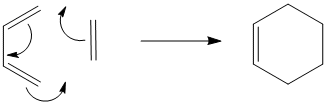
The Cope rearrangement of 1,5-hexadiene is seen below. The carbon atoms are numbered so the rearrangement can be seen more easily.

This reaction proceeds via a [3,3]-sigmatropic shift in a concerted fashion where the transition state is either a boat or chair structure, as shown below.

First, an anti periplanar conformer of the reactant was drawn and optimised using HF/3-21G level of theory. Using the same level of theory, a gauche conformer was drawn. The molecules were symmetrised and their point groups noted. This can be seen in the table below.

The energy and point group of two conformers of 1,5-hexadiene

Conformer
Energy (a. u. ):	-231.6925	-231.6917
Point Group:	Ci	C2

Generally, anti periplanar conformers have lower energy. This is because there is less steric hindrance with this structure. However, it was found in this case that a gauche structure had the lowest energy. Gauche structures have the lowest energy is some cases because, it is favourable to have H-H interactions at certain distances, and this particular structure allows lots of these kinds of Van der Waals interactions. However, the gauche conformer shown above was not the conformer with the lowest energy. The structure with the lowest energy was found to be the structure shown below, and is known as 'gauche3' in the reference table. It has the point group C₁ and the energy -231.6927 a. u. This corresponds to the one with the lowest energy in the reference table given. The previous anti corresponds to 'anti2' and the gauche corresponds to 'gauche2'.

The structure with the lowest energy was then optimised with a higher level of theory, B3LYP/6-31G*. This structure can be seen below. It has the energy -234.6117 a. u. This cannot be compared to the previous energies, as a different level of theory was used.

By comparison, the structures look virtually identical. However, certain dihedral and bond angles as well as bond lengths were measured and the results can be seen in the table below. The numbers correspond to the numbers seen on the reactant molecule in the above diagram.

A comparison of angles and bond lengths in optimised structures of the anti2 conformer

Property	1st Opt (B3LYP/3-21G)	2nd Opt (B3LYP/6-31G*)
Dihedral Angle: C1-C2-C3-C4	114.7o	118.5o
Bond Angle: C1-C2-C3	124.8o	125.3o
Bond Angle: C2-C3-C4	111.3o	112.7o
Bond length: C1-C2	1.32Å	1.33Å
Bond Length: C2-C3	1.51Å	1.50Å
Bond Length: C3-C4	1.55Å	1.55Å

The angles have been quoted to an accuracy of 0.1^o and the angles 0.01Å. It would be incorrect to quote them to more decimal places, as the calculations made to receive these results are not that accurate.

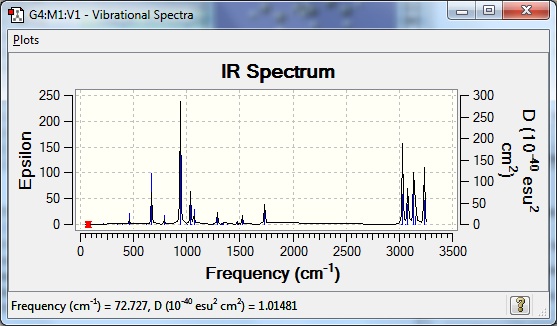
A frequency calculation was then carried out on the anti2 conformer to see if only real frequencies existed. This was confirmed as there were no negative frequencies. A table of the most important vibrations are shown below.

Vibrations of the anti2 conformer

Frequency (cm-1)	Animated Vibration	Description
1734		C=C stretch
3031		alkane C-H stretch
3080		alkane C-H stretch
3137		C-H stretch
3155		alkene C-H stretch
3234		alkene C-H stretch

The literature says that alkane C-H stretches occur at 2950-2800cm^-1 whilst alkene C-H stretches occur at 3100-3010cm^-1. The C=C stretch is said to occur at 1690-1630cm^-1. Therefore it can be seen that all the calculated frequencies are higher than the tabulated ones. This is expected as it is due to the estimations that the calculation makes about the nature of the bonds. It estimates them as harmonic oscillators, whereas in reality they are anharmonic oscillators. Another reason that the calculated frequencies may be higher is the complexity of the basis set used. The accuracy of the calculated frequencies would be improved by improving the basis set, but this computationally expensive and this is why it has not been done.

The spectrum has also been visualised below.

The energies from the part of the log file named 'Thermochemistry' are shown below.

Thermochemistry

Energy	Value (a. u.)
Sum of electronic and zero-point Energies	-234.469212
Sum of electronic and thermal Energies	-234.461856
Sum of electronic and thermal Enthalpies	-234.460912
Sum of electronic and thermal Free Energies	-234.500821

The Sum of electronic and zero-point Energies is the potential energy at 0 K including the zero-point vibrational energy (E = Eelec + ZPE).

The Sum of electronic and thermal Energies is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes (E = E + Evib + Erot + Etrans).

The Sum of electronic and thermal Enthalpies contains an extra correction for RT (H = E + RT), which is particularly important when looking at dissociation reactions.

The Sum of electronic and thermal Free Energies includes the entropic contribution to the free energy (G = H - TS).

After the optimisation of the reactants, the transition state chair and boat structures were also optimised. First a fragment, CH2CHCH2, was optimised using the HF/3-21G level of theory. Two of these were pasted into the same window, and arranged into a chair conformation. This structure was then optimised separately in two different ways.

The first was by computing the force constants at the beginning of the calculation and this only works well if the initial guess structure is close to the real one. The optimisation was carried out to a 'TS (Berny)'. The force constants were calculated once and Opt=NoEigen was typed into the additional keywords. Once optimised, the structure gave an imaginary frequency of 818cm^-1. This is animated below, and it can be seen that it corresponds to the connection/disconnection of the appropriate bonds for the cope rearrangement.

The second method was done by using the redundant coordinate editor. The reaction coordinate was frozen, using the keywords Opt=ModRedundant, and then the rest of the molecule was minimised. Once the molecule is relaxed, the coordinates can be unfrozen and the molecule optimisation can be started again. The carbon atoms involved in the reaction coordinate were frozen at 2.2Å apart. The optimised chair transition state of this molecule also had a vibrational frequency at -818cm^-1.

The bond forming/bond making bond length of the first optimised transition structure was 2.02046Å and for the transition structure optimised in the second way was 2.02079Å. It is usual to quote these lengths to two decimal places, and so therefore these two lengths are the same. Other bond lengths were the same, and bond angles were also the same to the required accuracy.

The energy of the transition state for structure optimised with the first method was -231.61932248 a. u. whereas the energy of the second transition state was -231.61932159 a. u. These energies are therefore the same as the small discrepancy is due to errors. It can be seen therefore that both of these methods are valid since they reach the same optimised transition state. They have their advantages and disadvantages which must be considered when using them for other molecules. The second method is more time consuming, but may be easier to get the right structure in the end. The first method is only good if the initial structure is close to the minima required.

The QST2 method was used to optimise the boat structure. The anti2 structure was opened and copied and pasted in the same window. These were viewed alongside each other and the atoms on the product were renumbered according to the numbering system seen at the beginning of the page. The job was submitted but with optimisation to a 'TS(QST2)'. The job failed, since the reactant nor the product resembled the boat transition structure. So the structure was then modified to this effect. The central dihedral angle was changed to 0^o , and the inside C-C-C bond angles changed to 100^o. This job was submitted to receive the transition structure. To prove this was the transition structure, a frequency analysis was done. One imaginary frequency was visualised at -840cm^-1. This means the transition structure was found. The vibration is shown below. The connection/disconnection of the bonds is asynchronous.

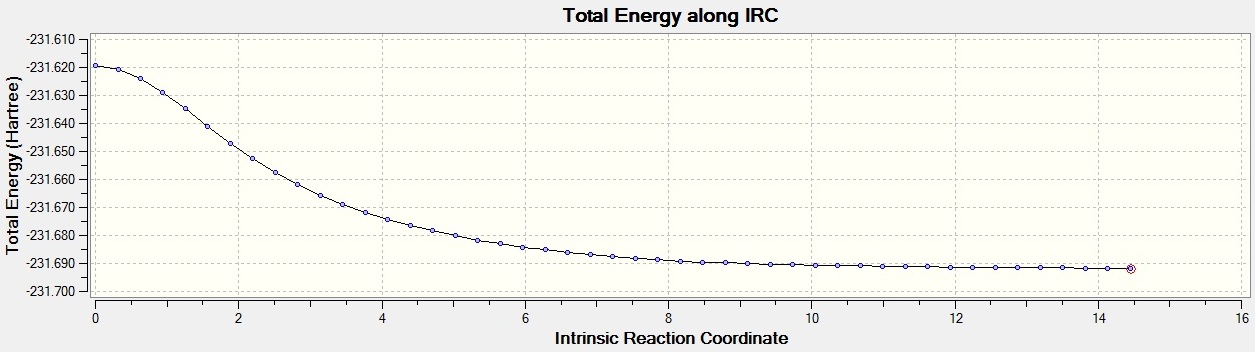
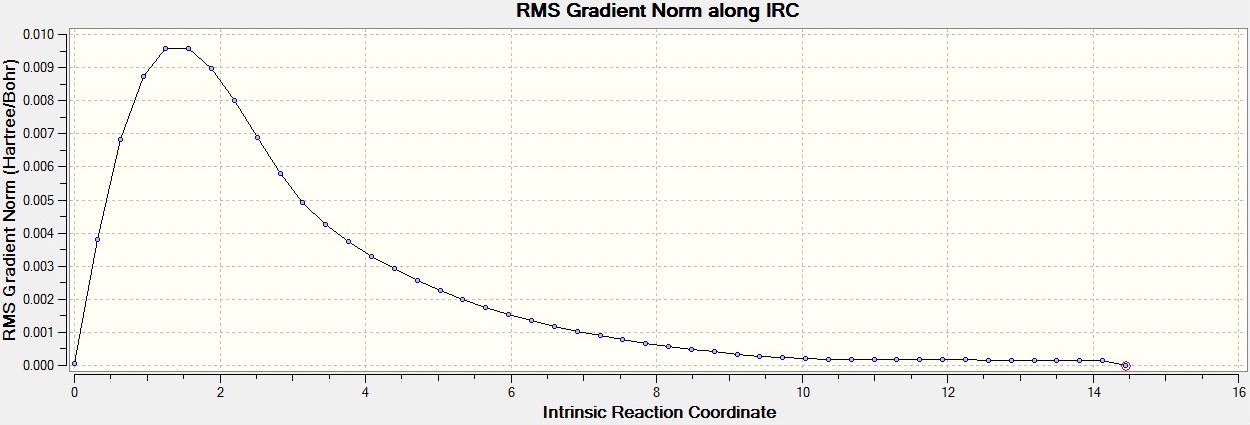
The boat transition state is thought to form the gauche1 conformer, and the chair transition state is thought to form gauche2. This is the closest structure that they resemble however, it is hard to tell what will happen in reality. However, the Intrinsic Reaction Coordinate which allows you to follow the minimum energy path from the transition structure to its local minimum on a potential energy surface. A series of points of small geometry steps along the steepest part of the slope are created. For the first calculation 50 points were taken along the IRC, as the default of 6 is not enough. Once this job had finished, it was seen that a minimum had not been reached. There were only 26 steps, so the job didn't terminate for the reason that it reached the limit of steps. In order to find the minima, two different methods were invoked. The first was to run the IRC again with the same method but with starting from the last structure from the previous calculation. This was done, but a minima was still not found. So, a different method was then used. The IRC was rerun from the beginning structure but this time calculating the force constants along every step. This turned out to be more reliable, though more expensive, since the optimum structure was found in 47 steps. This was confirmed to be a minimum when the structure was optimised and the resulting molecule was the same. The molecule is shown below:

It can be seen that this corresponds to the gauche2 structure.

Here is the progression of the IRC by the second method.

Starting from the HF/3-21G optimised structures of the chair and boat, the structures were optimised again using the B3LYP/6-31G* level of theory. Comparisons for the two differently optimised chair and boat structures are shown below.

Chair transition state optimisation

	3-21G	6-31G*
Energy (a. u.)	-231.6193	-234.5570
C-C-C Bond Angle	120.5o	120.0o
Bond forming/breaking Bond Length	2.02Å	1.97Å
C-C Bond Length	1.39Å	1.41Å

Boat transition state optimisation

	3-21G	6-31G*
Energy (a. u.)	-231.6028	-234.5431
C-C-C Bond Angle	121.7o	122.3o
Bond forming/breaking Bond Length	2.14Å	2.21Å
C-C Bond Length	1.38Å	1.39Å

It can be seen that the geometries between the two optimisations are similar, and there is not much difference between the angles and lengths. The energies however are markedly different. These cannot really be compared since a different level of theory was used to work each out. The literature shows that the interallyl bond length should be 2.062Å. Therefore it can be seen that the values obtained here are close to this, and therefore the calculation and basis set used were good since they closely resemble reality. The activation energies were worked out at both levels of theory and for each transition structure, and are compared to experimental values in the table below.

Activation Energies at 0K (kcal/mol)

	HF/3-21G	B3LYP/6-31G*	Experiment
Chair	45.93	34.32	33±0.5
Boat	56.29	43.05	44.7±2.0

The activation energy for the chair transition state is lower than for the boat. This is also what is seen in the literature. The chair transition state gives less steric hindrance and so has a lower activation energy barrier. The calculated values are close to literature for the calculations where the higher level of theory is used. Therefore, it can be seen that this basis set is better and works well for this system as it creates accurate results. However, using the lower level of theory first and then going on to use this structure for the higher level of theory is a good method, as it is more computationally efficient.

Using the thermochemistry data, a table has been compiled showing the energies corresponding to the one in the reference table given. The energies match very closely, and so the correct transition states and the correct anti2 structure were found.

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61932159	-231.466696	-231.461336	-234.55698130	-234.414905	-234.408980
Boat TS	-231.60280243	-231.450927	-231.445299	-234.54309307	-234.402342	-234.396009
Reactant (anti2)	-231.69253529	-231.539540	-231.532568	-234.61170278	-234.469212	-234.461856

The Diels Alder Cycloaddition

The Diels-Alder reaction is a cycloaddition between a diene and a dienophile. π orbitals of the dieneophile are used to form new σ bonds with π orbitals of the diene. The HOMO/LUMO of one of the fragment interacts with the HOMO/LUMO of the other and forms two new bonding and anti-bonding MOs. The most simple of these reactions is between ethylene and cis-butadiene. This will be studied along with a case where the reactants have substitents, such as is the case for maleic anhydride (the dienophile) and cyclohexadiene (the diene). Transition structures for these reactions was found by using the AM1 semi-emperical molecular orbital method.

Ethylene and Cis-butadiene

Here is the reaction scheme.

Firstly cis-butadiene and ethylene were optimised separately with the AM1 method, and the molecular orbitals were plotted.

Molecular Orbitals

	Molecule	HOMO	LUMO
Cis-butadiene
		Antisymmetric	Symmetric
Ethylene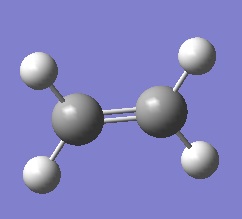
		Symmetric	Antisymmetric

The transition structure was found using the freeze co-ordinates method. Firstly, the TS (Berny) method was used, but the minima was not located, and so the structure was not optimised. The two optimised fragments were pasted into the same window, and frozen at 2.2Å apart, then optimised to a minimum. The structure was unfrozen, and then optimised as a transition state. This was a better method, since the minimum was found. This was confirmed by the presence of one negative frequency at -956.96cm^-1 in the frequency analysis. This frequency is shown below. It can be seen that the bond formation is synchronous, which is evidence for the fact that this reaction is concerted.

The lowest real frequency is seen at 147cm^-1 and this is animated below. It is seen that it is a wagging mode rather than the stretching mode that was seen above. The real frequency is also different in that it is asynchronous.

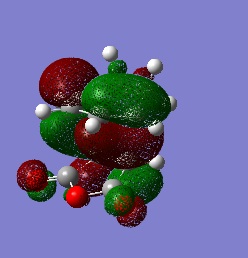
This are the HOMO and the LUMO and it can be seen that the HOMO is antisymmetric.

Molecular Orbitals of transition state

HOMO	LUMO

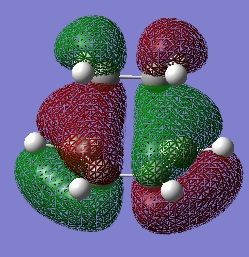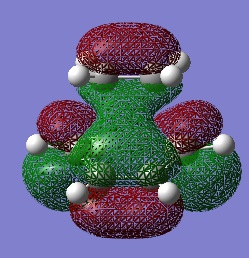
These are formed by interaction of the MOs with the same symmetry, as these are the only ones that are allowed. The HOMO of the cis-butadiene interacts with the LUMO of the ethylene, as these are both antisymmetric and hence forming the HOMO of the transtion state. Whilst the LUMO of the cis-butadiene interacts with the HOMO of ethylene, as these are both symmetric, thus forming the symmetric LUMO.

The molecule can be seen here.

Here are some of the angles and lengths, in order that the structure can be analysed.

Geometry of Transition State

	From Fragments	Transition State
Partly formed bond length	N/A	2.12Å
Ethylene C=C length	1.33Å	1.38Å
Butadiene C=C length	1.34Å	1.38Å
Butadiene C-C length	1.45Å	1.40Å
Butadiene C=C-C angle	125.7o	121.2o

The C-C distance for the formation of the new bond was found to be 2.12Å. This is significantly longer than any of the other C-C bond lengths, and this is obviously because this is the transition structure, and the bonds have not formed yet. It can be seen in the transition state that the various C-C bond lengths are more uniform than the C-C bond lengths from the individual fragments, again, indicative of a transition state, as the bond lengths in the product would be expected to be approximately equal. The bond angle has reduced in the transition state, which is also expected, as the internal angles within a hexagon (or six membered carbon ring) are 120^o.

A typical sp² C-C bond length was found in the literature to be 1.3Å whilst a typical sp³ bond length was 1.54Å. In the above fragments, it can be seen that bond length measurements are close to the literature, but in the transition state, The Van der Waals radius of the carbon atom is 1.70Å. This is smaller than the partly formed bond length, but larger than the bonds already formed. This is the expected outcome.

Cyclohexa-1,3-diene and Maleic Anhydride

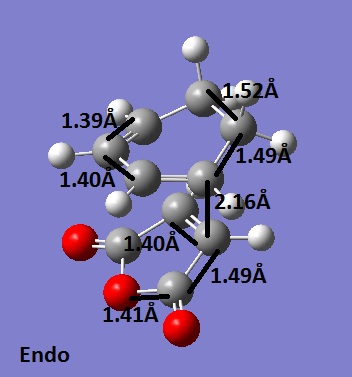
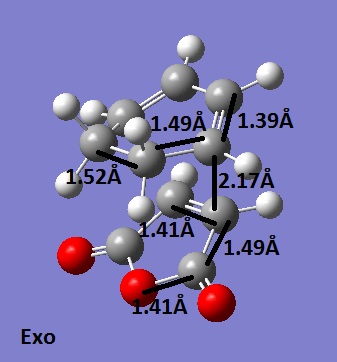
These molecules react to give the endo adduct as the major product. The regiochemistry is controlled by π orbitals on the dienophile, by virtue of their symmetry. The presence of these extra orbitals contributes to the bonding and so gives that structure extra stabilisation. This is known as the secondary orbital effect. It is thought that as the reaction is kinetically controlled, the exo product has a higher energy. Using the frozen co ordinates method once again, both of these transition structures were located. They were confirmed as transition states because both had one negative frequency.

The endo structure had a negative frequency at -806.92cm^-1

The exo structure had a negative frequency at -812.23cm^-1

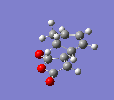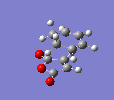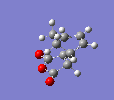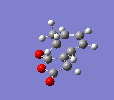
The important bond lengths for the endo structure are shown.

The C-C through space bond length between the (C=O)-O-(C=O) and the CH=CH was found to be 2.89Å.

The important bond lengths for the exo structure are shown.

The C-C through space bond length between the (C=O)-O-(C=O) and the CH₂-CH₂ was found to be 2.94Å.

HOMOs of the transition structures

Endo	Exo

The endo structure optimisation shows that the fragments are closer together (shown by the bond forming bond length and the C-C through space length in particular), thus supporting the idea that this is the major product, as it is favourable for the reactants to be in a close proximity and therefore react. The other bond lengths are about the same, but due to the orientation in the exo structure, the longer C-C makes the C-C through space bond longer. The energy for the endo structure was -0.05150445 a. u. and the energy for the exo structure was -0.05041928 a. u.

It can be seen that in the endo structure, the two alkene bonds are positioned closely to the two carbonyl groups whereas in the exo structure, they are positioned further away. It is more favourable to have them close because this allows for the secondary orbital overlap effect to come about as there is significant orbital overlap between the orbitals of the diene and the orbitals of the dienophile.

In the (C=O)-O-(C=O) part of the molecule, for exo, it seen that there is no electron density, and thus no positive orbital overlap, and so this structure is less stabilised. There is more strain in the exo structure, than the endo, which is another reason for its increased instability.

Overall, it can be seen that the endo structure, although thermodynamically less stable, is the product observed, mainly due to the positive orbital overlap, which allows the orbitals of the same symmetry on the two fragments for the endo structure to overlap, and hence stabilise this structure. In addition to this, there is contribution from the substituents, making the transition state even more stabilised. The exo structure does not have this kind of stabilisation and hence is strained.

In conclusion, it can be seen that gaussian can predict the most stable structure based on the energy, and human observation of the orbitals. However, it is limited since there is an error of ~0.038 a. u. and so if there is only a small energy difference between the two transition states, it can be hard to tell which one is the major one. Gaussian is only making calculations on this one molecule as created in gaussview, whereas in reality there would be many more molecules all affecting each other and all in slightly different conformations, and so it would be better if the calculation took into account statistical mechanics using a boltzmann distribution. Of course, all the energy calculations are approximated and at different levels depending on the basis set used. And so, all the energy approximations can be improved and be closer to the energies seen in reality if a better basis set is used.