Rep:Mod:hgmd1

Modelling using Molecular Mechanics

Using Molecular Mechanics, it can be seen which conformer of a certain molecule is the most stable. The model uses data it has about which bond lengths between specific atoms are ideal, and any deviation from this it gives a kind of energy penalty. The model does the same for any other deviations from ideality for bending, torsion, Van der Waals forces and dipole/dipole forces. Using varying sizes of basis sets will vary the accuracy of the answers. However the efficiency is compromised because the larger basis sets take much longer to do.

The Hydrogenation of Cyclopentadiene Dimer

At room temperature, cyclopentadiene dimerises, for which the reaction scheme is shown below, giving two products; the endo and the exo dimer, which can be seen (as a jmol) along with their energies below.

It can be seen that the transition state of the endo product is less sterically hindered and therefore is more likely to form, therefore making the endo form the minor product.

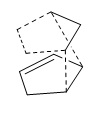
The exo (1) and endo (2) dimers were modelled and are shown below.

‎

Energy Breakdown (kcalmol^-1) for Molecules 1 and 2

Type	Molecule 1	Molecule 2
Stretch:	1.2729	1.2611
Bend:	20.5787	20.8214
Stretch-Bend:	-0.8332	-0.8408
Torsion:	7.6769	9.5211
Non-1,4 VDW:	-1.4200	-1.5452
1,4 VDW:	4.2365	4.3363
Dipole/Dipole:	0.3781	0.4488
Total Energy:	31.8898 kcal/mol	34.0026 kcal/mol

So, in fact, the product with the higher energy is actually observed. Therefore the observed endo product is known as the thermodynamic product. Whereas the exo product, although it has the lower energy, is not seen and is known as the kinetic product. The individual energies for each component of the total energy are very similar for both isomers. However the energy showing the most difference is the torsion component. Meaning more energy is needed as a result of the twisting of the bonds in the endo dimer, which is why the total energy is more than in the exo dimer.

The dimer can then be hydrogenated to give one of two products.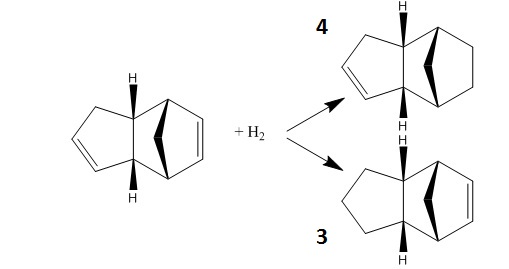

The two hydrogenated products' relative energies are shown in the tables below:

Energy Breakdown(kcalmol^-1) for Molecules 3 and 4

Type	Molecule 3	Molecule 4
Stretch:	1.2779	1.0963
Bend:	19.8726	14.5074
Stretch-Bend:	-0.8360	-0.5493
Torsion:	10.7691	12.4972
Non-1,4 VDW:	-1.1724	-1.0507
1,4 VDW:	5.6308	4.5124
Dipole/Dipole:	0.1622	0.1407
Total Energy:	35.7042 kcal/mol	31.1540 kcal/mol

Molecule 3 has significantly more contribution for the bending component of the energy, which is justified by the fact that the bond angle is calculated to be 108^o, which is particularly different from the optimal alkene angle of 122^o. The bond angle for molecule 4 is 112^o, which is closer to the optimal angle and so the "penalty" bending energy is less, thus contributing to overall energy being less than that of molecule 3. As Molecule 4 has the lower energy, this means the double bond in the cyclohexene is more easily hydrogenated.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD⁺ analogue)

Molecule 5 is a Prolinol derivative and is an optically active compound. When reacted with methyl magnesium iodide gives the product 6 with the stereochemistry shown, as the reaction is highly regio- and stereo- selective.

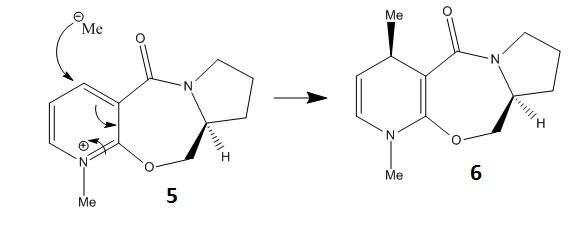
The molecule was modelled using molecular mechanics and by changing the conformation slightly, in order that the dihedral angle between the carbonyl and the aromatic ring could be measured and along with the relative energy be compared to one another to see what the optimum configuration was. The reactant 5 can be seen below.

The list of energies and angles are tabulated below.

Total Energies and Dihedral Angles for Molecule 5

Total Energy (kcal/mol)	Dihedral Angle
43.1118	10.6557
44.6298	-11.3416
188.2334	-11.8453
297.4164	-33.1365
43.1495	8.3312

The literature suggests that there are only two conformation minima possible. One of which the carbonyl is above the plane of the pyridine ring anti to the hydrogen atom at the chiral centre and the other conformer has the carbonyl group and pyridine ring coplanar. It suggests that there are no conformers with the carbonyl below the ring. The data extracted from using Molecular Mechanics would suggest that the only two viable angles are 8^o and 11^o. These could correspond to the two conformers, however they are very close and even the lower angle cannot really be used to describe two groups that are coplanar. The calculated angle of 33^o is almost certainly not observed since the energy is too high at 297 kcalmol^-1. The stereochemistry seen in the reaction scheme is that despite the small dihedral angle, when the molecule is attacked by MeMgI, the magnesium atom coordinates itself to the oxygen from underneath and so to avoid a steric clash the methyl group will attack from above.

A similar reaction of another pyridinium ring (molecule 7) with aniline was also modelled in the same way.

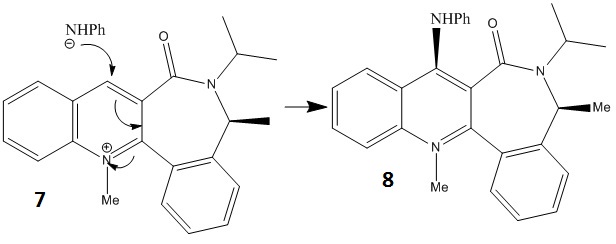
A link to the reactant molecule is given.

And its energies and corresponding angles are:

Total Energies and Dihedral Angles for Molecule 7

Total Energy (kcal/mol)	Dihedral Angle
66.5119	-21.4824
63.4288	20.5482
258.1695	21.0575
369.8821	46.9472
62.6971	-20.2741
302.5277	-49.192
151.6324	-91.4107
86.9202	-124.7601

The literature shows that the product in the reaction may give two isomers. The Molecular Mechanics method cannot take into account the reaction scheme and will not calculate the energy if there are two molecules in the window, and so the results shown here may not necessarily match those in the literature. The stereocontrol seen in the reaction scheme seen above is due to other groups in the molecule. The carbonyl points down in space due to the methyl and isopropyl groups that point upwards. This makes the attack of the aryl group more facile if the attack is from above and there is less clash with the oxygen's lone pears.

A way to improve upon using the simple MM2 Molecular Mechanics model is to use MOPAC instead. This uses algorithms that take into account molecular orbitals and so as a result is much more accurate. This method was used later on for the regioselective addition of dichlorocarbene.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

An intermediate step in the synthesis of the drug taxol involves the molecule pictured below, which can isomerise. The type of isomerism seen is atropisomerism. These molecules are conformers of one another, but due to the very high energy barrier to rotation of a particular bond, they can be isolated.

It was found that the isomer 10 was more stable. Before optimisation the energy molecule 10 was 54.5021 kcal/mol with the MM2 force field option and 77.8558 kcal/mol with the MMFF94 option. After optimisation, which involved changing the structure of the cyclohexane ring from a boat like structure to a chair, the MM2 energy was given as 49.4695 kcal/mol. This is the molecule shown in the link.

Molecule 9 had a slightly higher energy of 58.1248 kcal/mol. The reason that molecule 9 has a higher energy is that the position of the carbonyl group locks the cyclohexane ring into an energetically expensive twist boat conformation, whereas the position of the carbonyl in molecule 10 allows the cyclohexane to be in the more stable (and therefore energetically favourable) chair conformation. As these molecules are in equilibrium, molecule 9 will isomerise into molecule 10 to avoid the unfavourable interactions. The alkene functionality on these molecules is particularly stable and as a result reacts very slowly. Molecules of this type are known as 'Hyperstable Olefins', and have negative olefin strain energies, which means that the strain energy of the olefin is less than that of its parent hydrocarbon. It is therefore thermodynamically unfavourable to hydrogenate the bond, hence the slow reaction time. It is the position of the double bond which determines this particular property. In this molecule one end of the double bond, which lies within a medium-sized polycyclic system, terminates at a bridgehead.

Modelling using Semi-Emperical Molecular Orbital Theory

This model is slightly more sophisticated than using the force field methods to calculate the energy. Yet, it is not as complicated as solving the schrodinger equation. It uses elements of both. The simplifications of EΨ= HΨ involve emperically derived parameters to make calculated values more similar to observed values.

Regioselective Addition of Dichlorocarbene

The reaction scheme for tetrahydronaphthalene with dichlorocarbene is shown below.

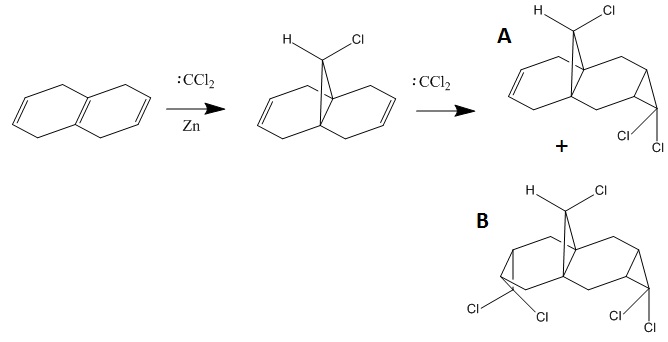
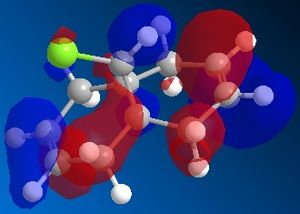
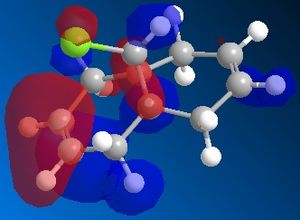
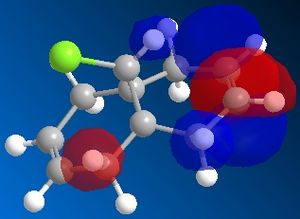
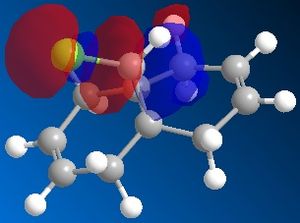
72% of Molecule A (the mono-adduct) and 23% of Molecule B (the di-adduct) are seen when the above reaction takes place and the remaining 5% could not be isolated. Calculations and observations of the Molecular Orbitals can help explain the reactivity seen in the above reaction. The Molecular Orbitals for 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene are shown below.

Molecular Orbitals for compound 12

HOMO-1	HOMO	LUMO	LUMO+1	LUMO+2

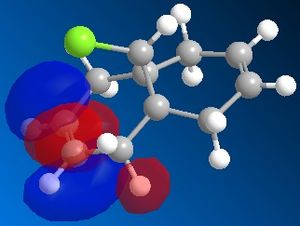The HOMO looks the same as the HOMO in the literature, which shows that there is a lot of electron density around the syn-alkene. As dichlorocarbene is an electrophile, it will attack the alkene with the most nucleophilic character which, according to the HOMO picture, is the double bond syn to the chlorine. Hence, the only isolated mono-adduct is the one where the anti alkene remains. Another contribution to the higher reactivity of the syn alkene, is the anti-periplanar interaction between the C-Cl σ* and the anti alkene π orbitals, which stabilises the double bond by lowering the energy of the orbital and thus making it less susceptible to attack.

The same program was used to also predict the IR spectra. and the IR stretching frequencies are tabulated below.

Stretching Frequencies (cm^-1)

Derivative	C-Cl stretch	Anti-alkene stretch	Syn-alkene stretch
Di-alkene (Compound 12)	770.81	1737.03	1757.44
Monoalkene	774.98	n/a	1758.07
with OH group	771.52	n/a	1778.73

The C-Cl stretch literature value was found to be 785-540cm^-1, and the predicted values lie within this region. The literature value for an alkene was found to be 1690-1630cm^-1, and the predicted values for this are ~100 wavenumbers too high. The reasons for this are two fold; first of all the program that predicts the IR frequencies uses an ideal harmonic, which models the bond as a spring, and the atoms as balls. In reality, non-idealities exist and the stretch is anharmonic. Also, the basis set used,6-31G, was of a medium level, and so was not as accurate. The accuracy of the predictions can be improved by changing the size of the basis set and also by changing the harmonic model to an anharmonic one. However, this complicates the calculation a lot, and therefore takes up a lot more power and time. It would take too long and this is why it has not been done.

It can be seen that the syn-alkene stretch has a higher wavenumber, this means more energy is required to carry out the stretch and therefore it is a stronger bond. It would be expected that a stronger bond would be harder to attack. However, the IR stretching frequencies take into account both the π and σ bonds, whereas the reactivity is purely based on the π bond, and so perhaps the σ bond is particularly strong. Also, quite obviously, the two double bonds have different locations within the molecule, and as the stretching of a bond affects the whole molecule (as can be seen by the animations), the location may help determine the wavenumber as the chlorine in the bridge will affect how well these bonds can stretch.

The strength of the C-Cl improves slightly with the hydrogenation of the anti-alkene whereas the syn-alkene stretching frequency remains near enough constant. This suggests that the syn-alkene bond remains unaffected by the absence of the anti-alkene. An OH group was added to the mono-adduct, anti to the chlorine to see how this affected the other bonds in this molecule. The C-C, remains unaffected whereas the syn-alkene's wavenumber rises, meaning a stronger bond. The hydroxyl group is a resonance donator and so adds alectron density to the molecule which may be best received by the π bond in the alkene, and then it could be assumed the bond strengthens, as it is being donated into a bonding orbital.

The stretches associated with C-H bonds are represented on the spectrum as having large peaks, and this is expected. Generally, it can be seen that the program and basis set selected give a good prediction for the IR spectra, with the (easy to correct) exception that each peak is about 100 wavenumbers out. Both molecules have the C_s symmetry point group since they both possess the σ^h symmetry element, meaning they have a symmetry plane.

Structure based Mini Project using DFT-based Molecular Orbital Methods

A journal was selected that showed a reaction where the products gives a mixture of isomers, so this could be studied. The two molecules that were isomers of each other were drawn on ChemBio 3D and their structures optimised using MM2. They could then have their structures changed by hand to see which had the structure with the lowest energy. The structures were then also optimised with the MOPAC/PM6 method as well. The structure was further refined with the DFT method. On receiving this file, this could be sent again for an NMR shift calculation.

Origin of Chiral Induction in Radical Reactions with the Diastereoisomers (5R)- and (5S)-5-l-Menthyloxyfuran-2[5H]-one

The following reaction yielded a mixture of two diastereoisomers, (5R)- and (5S)-5-l-menthyloxyfuran-2[5H]-one from acetalization of 5-hydroxyfuran-2[5H]-one with l-menthol. The (5R) molecule is labelled as 1, and the (5S) molecule is labelled as 2.

The molecules were drawn on ChemBio 3D are shown below.

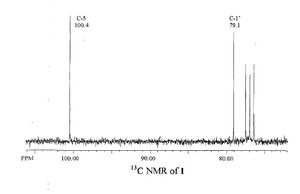
The literature and the calculated NMR spectra are shown below.

NMR Spectra for Molecule 1

Literature	Calculated

The literature only showed peaks above ~70ppm, therefore the calculated one has been altered so it shows this too for easier comparison. Only two peaks are labelled on the literature spectrum and these have been compared to the peaks that they correspond to in the calculated spectrum in the following table. The literature peaks that are not labelled are thought to be solvent peaks, as also, these do not appear in the calculated spectrum.

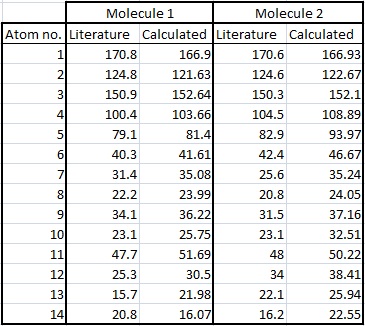
The picture gives the atoms labels so they can be easily recognised.

NMR Peaks for Molecule 1

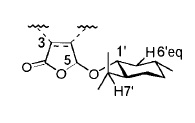
Atom No.	Literature Shift	Calculated Shift	Difference
C-5	100.4	103.661	3.261
C-1'	79.1	81.402	2.302

It can be seen that there is very little difference between the literature values and the calculated values. This is good, as it means the structure calculated by the program was very close to the actual structure as proposed by the literature and therefore the calculations used are good approximations.

NMR Spectra for Molecule 2

Literature	Calculated

NMR Peaks for Molecule 2

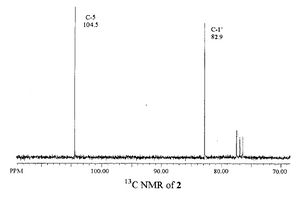Atom No.	Literature Shift	Calculated Shift	Difference
C-5	104.5	108.890	4.390
C-1'	82.9	93.965	11.065

In this case the differences are more marked. The calculated shift is ~11ppm higher than the literature value, this is quite significant. It seems to be that the approximations made in the calculation for molecule 2 were not good enough. This is the best explanation as it can't be that the other atoms in the molecule 2 affected the accuracy (eg O atoms), as they are the same ones as in molecule 1! Therefore, any discrepancies with interference from other atoms or functional groups would affect both molecules.

Below, all the NMR peaks are assigned to atoms for molecules 1 and 2 in order that they can be compared, and the number labelled molecule corresponds to the numbers in the table. The graphs show the differences between the calculated and literature values.

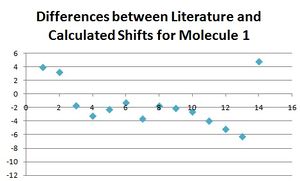
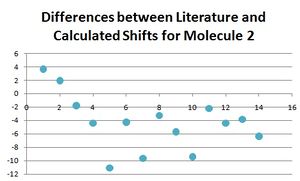
The differences for nearly all of these peaks is larger for molecule 2 than for molecule 1. This is not the case for the first four atoms which are the carbon atoms in the furan ring. This could be for the reason that for both molecules, this part of the molecule remains the most unchanged, and so the differences between calculated and literature are constant for both. Experimental NMR takes into account all the conformers of the molecule (even if they only differ slightly) that exist at room temperature (or whichever temperature the NMR spectrum is taken at), whereas the calculated NMR has only taken into account one conformer. It would make sense that the reason the data fits well for molecule 1 (but not perfectly) is that the major conformer was found. Whereas, the reason the data did not fit for the molecule 2 as well is that perhaps a minor conformer was modelled on the program, and therefore the data did not match as well. There would be a be a better fit for the data for molecule 1 if one of the calculated peaks was omitted and the other values moved along. Apart from this, it can be seen that for molecule 1 the literature and calculated values fit well, with the largest difference being only 4, and hence the approximations made in the program calculating the spectra are adequate and close to what is seen in reality.

Between the two isomers, it can be seen that the main differences in the literature peaks are between carbon atoms on side chains of the ring, such as the methyl and the isopropyl groups. The rest of the carbon NMR assignments are particularly close, and so the orientation of these side chains must change reasonably significantly. This difference between the two spectra could be used to distinguish the two isomers, however this would be quite difficult, and other techniques would be better, such as measuring the optical rotation.

Overall, it can be seen that the program has predicted the NMR spectra well, and the peaks are approximately where you would expect them to be and so the program, calculations and basis set were a good selection. However, it is limited by the fact it takes the spectrum of the static molecule, and cannot take into account atoms that exchange with each other, and it does not know which atoms are equivalent.

NMR spectroscopy could not be used to distinguish these products as can be seen from above, their spectra are too similar. After viewing the proton NMR spectra from the literature, these were more different than using the carbon NMR technique. This must be at least down in part to the differing position in space of the hydrogen at the 5 position.

The energy of each isomer was calculated to be 39.61kcalmol^-1 and 38.47kcalmol^-1 respectively for molecules 1 and 2. As there is such little difference in the energy, this corresponds well with the fact that the literature states that both products were yielded in equal amounts.

The literature gives values for certain distances in the molecule. These are as follows:

H-H distances in Molecule 1(Å)

Atoms	Literature	Calculated
H5-H6'	2.36	4.2071
H5-H7'	4.41	4.5080

The H5-H7' distance is quite close in value, whereas the H5-H6' distance doesn't match. This means that the model made did not match the actual structure found in the literature. More conformations must be tested to see which ones fit the literature data better. It is thought perhaps that one of the bonds was twisted the wrong way to create an H-H distance that is ~2Å out.

The best way to tell apart these two isomers would be to measure their optical rotations, and these could also be compared to literature values. This can be done using a full quantum mechanical calculation, however it is generally found that these calculations are inefficient as they take a long time and the results are not that close to the ones in reality.

In conclusion of the mini project, it can be seen that the approximations made in the calculations work well to an extent but cannot be completely relied upon to give accurate results representative of what is seen in reality. Even if a larger basis set was used, the model is still limited by other approximations it makes and by the fact that the model is static and only one of a varying array of slightly different conformers.