Rep:Mod:hgl0903

Module 3: Transition States and Reactivity

Introduction

Apart from studying the structures and bonding of molecules, computational chemistry is also a powerful tool used to study the transition states and reactivity of molecules. In this modules, the transition structures on potential energy surfaces for the Cope rearrangement and Diels Alder cycloaddition are characterised using orbital-based methods. The reaction paths and barrier heights are calculated as well.

The Cope Rearrangement

The [3,3]-sigmatropic rearrangement undergoes via the following reaction scheme:

There are two possible transition structures, a chair and a boat. The boat is known to have a higher energy than the chair. In this experiment, such activation energies and enthalpies are calculated using Gaussian09W.

Optimising the Reactants and Products

Optimisation of 1,5-hexadiene

The anti structure was optimized at the HF/3-21G level with %mem=250MB. The structure obtained after optimisation has a point group of C2. A gauche structure was created by adjusting the dihedral angles of the optimised anti structure, submitted with the same setting used for the anti one. The point group obtained is also C2. The summary of optimisation of both structures are shown below. It would be expected the anti structure has lower energy than that of the gauche one since there are less steric effect.

optimisation of anti1 linkage structure

optimisation of gauche2 linkage structure

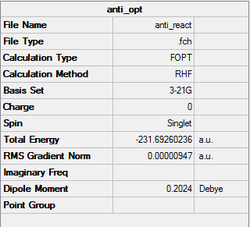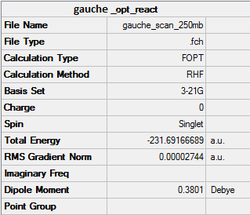Referring to Appendix 1, it is found that the anti structure obtained is anti1 while the gauche structure obtained is gauche2.

Optimisation of 1,5-hexadiene of C₂ symmetry

Structures	Total Enegy (a.u.)	Energy (kJ/mol)
anti1 anti1	-231.69260	-145389.3
gauche2 gauche2	-231.69167	-145388.7

The results do agree with the prediction. Since the four centre carbons on anti1 all have antiperiplanar confomations, it was predicted to be the one having the lowest energies. To test my hypothesis, several anti and gauche structures were tested and the results are all summarized in the Table 1.

Table 1: Optimisation of different conformers of 1,5-hexadiene

Conformers	Total Energy(a.u)	Point Group	Relative Energy (kcal/mol)	References
anti1	-231.69260	C2	0.04	DOI:10042/to-57902
anti2	-231.69254	Ci	0.08	DOI:10042/to-58114
anti3	-231.68907	C2h	2.25	DOI:10042/to-57929
anti4	-231.69097	C1	1.06	DOI:10042/to-58343
gauche1	-231.68772	C2	3.10	DOI:10042/to-57930
gauche2	-231.69167	C2	0.62	DOI:10042/to-57903
gauche3	-231.69266	C1	0.00	DOI:10042/to-58234
gauche4	-231.69153	C2	0.71	DOI:10042/to-58118
gauche5	-231.68962	C1	1.91	DOI:10042/to-58543
gauche6	-231.68916	C1	2.20	DOI:10042/to-58544

Surprisingly, gauche3 turns out to be the one having the lowest energy and the predicted structure anti1 is the 2nd lowest energy among the tested structures. However, the difference between them is not significant. A further test was carried out using B3LYP/6-31G* levels. The results obtained do agree with the prediction. The results are shown in Table 2.

Table 2: Optimisation at B3LYP/6-31G*

Conformers	Total Enegy (a.u.)	Relative Energy (kcal/mol)	Point Group	DOI
anti1	-234.61179	0.00	C2	DOI:10042/to-58564
gauche3	-234.61133	0.29	C2	DOI:10042/to-58562

After optimisation at higher levels, anti1 has the lowest energy than that of gauche3, which agrees with my prediction. However, the high stability of gauche3 is due to the stabilisation resulted from overlap of the C=C π orbital with the C-H σ orbital, dominant over the steric repulsion within the structure.

C_i anti2 conformer

Optimisation of C_i anti2 conformer

C_i anti2 of 1,5-hexadiene was also optimised at the B3LYP/6-31G*. The final structures are compared in Table 3. The structures are symmetrical and therefore only half of the bond lengths and dihedral angles are reported.

Table 2: Optimisation at B3LYP/6-31G*

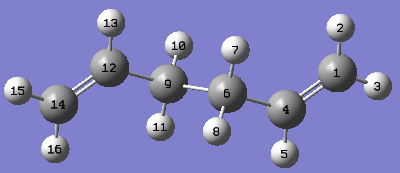
	Total Enegy (a.u.)	Point Group	Bond Length (Å)	DOI
anti2 optimised at HF/3-21G	-231.69254	Ci	C(14)=C(12) 1.32; C(12)-C(9) 1.51; C(9)-C(6)1.55; C(14)-H(15) 1.07; C(12)-H(13) 1.08; C(9)-H(10) 1.09	DOI:10042/to-58114
anti2 optimised at B3LYP/6-31G*	-234.61171	Ci	C(14)=C(12) 1.33; C(12)-C(9) 1.50; C(9)-C(6)1.55; C(14)-H(15) 1.09; C(12)-H(13) 1.09; C(9)-H(10) 1.10	DOI:10042/to-58419

The C=C double bonds become longer and the C-C bonds are shorted after optimisating at the higher DFT/6-31G*. The difference between the enegy is about 2.9 a.u. which is equivalent to 7614kJ/mol. The overall geometry roughly stays the same.

Frequency Analysis

A frequency calculation was submitted to SCAN using the optimised anti2 conformers obtained at B3LYP/6-31G*. All vibrational frequencies obtained are real and positive. In addition, another frequency calculation was carried at 0K by setting the temperature at 0.00001K and pressure at 1 atm. The results are shown below. It is found that at absolute zero temperature, all four sums are the same. The sum of electronic and zero-point energies of the one at 298.15K roughly agrees with the one obtained at 0K.

Frequency Analysis of anti2 conformer

	Frequency analysis at 298.15K	Frequency analysis at 0K
IR spectrum
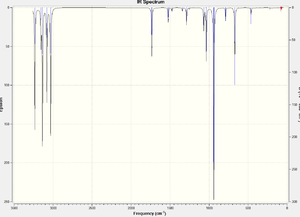
Sum of electronic and zero-point energies (E=Eelec+ZPE) (a.u.)	-234.469204	-234.468766
Sum of electronic and thermal energies (E=E+Evib+ Erot+Etrans) (a.u.)	-234.461857	-234.468766
Sum of electronic and thermal enthalpies (H=E+RT) (a.u.)	-234.460913	-234.468766
Sum of electronic and thermal free energies (G=H-TS) (a.u.)	-234.50077	-234.468766
DOI	DOI:10042/to-58427	DOI:10042/to-58598

Optimizing the Chair and Boat Transition Structures

In this section, the chair and boat transition structure optimisations for the Cope rearrangement were set up by

1. computing the force constants at the beginning of the calculation;
2. using the redundant coordinate editor;
3. using QST2.

IRC(Intrinisic Reaction Coordinate) of both structures were run and the activation energies for the rearrangement via both transition structures were obtained.

Chair Transition State

An allyl was created using GaussView 5.0. It was optimised using the HF/3-21G level of theory. The chair transition state was created using two of such fragment, the distance between the terminal ends of the fragments was set to 2.2Å. The chair structure was then optimised by using the methoeds mentioned in the previous section.

• Chair(b): Optimisating by Computing the force constants at the beginning of the calculation

The created chair transition states was optimised to a TS(Berny) by calculating the force constants once with Opt=NoEigen at the additional keyword box and a frequency calculation was also included. The calculated structure is a C_2h chair. The terminal ends of the two fragments are 2.02Å apart. In the frequency analysis, an imaginary frequency is found at -818cm^-1, which confirms the existence of the transition state. The animated vibration is shown below.

imaginary vibration of the chair transition structure

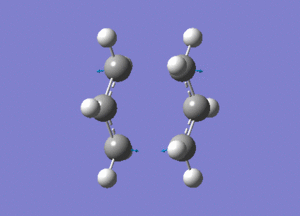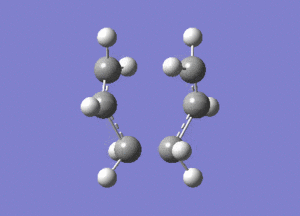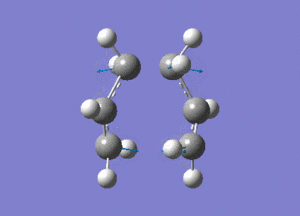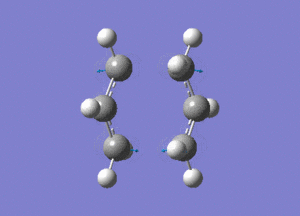
• Chair(d): Optimisaing using the redundant coordinate editor

The tranistion structure was optimised again using the frozen coordinate methods. The distances between the terminal C ends were freezed to 2.2Å and was optimised to a minimum with Opt=ModRedundant included in the input file. The optimised structure (chair (c)) looks similar to the one obtained from the previous section. Since the terminal distance was freezed, the distance between them is still 2.2Å. A further optimisation was set up using Redundant Coord Editor. The Bond was set to Derivative and a transition state optimised was set up with calculation of the force constant set to Never. The obtained structure looks again the same as the ones obtained in the previous section, and the distance between the terminal C ends is also the same, 2.02Å.

Optimisation of chair transition state

Optimisation methods	Optimisating by Computing the force constants at the beginning of the calculation	Optimisaing using the redundant coordinate editor (freezed bond length)	Optimisaing using the redundant coordinate editor (derivative bond length)
Energy (a.u.)	-231.61932	-231.61519	-231.61932
Terminal C ends distance(Å)	2.02	2.20	2.02
Jmol	chair(b)	chair(c)	chair(d)
DOI	DOI:10042/to-58130	DOI:10042/to-58129	DOI:10042/to-58136

Boat Transition State

The boat transition state was optimised using QST2 method. The reactant molecule used was anti2 conformer. Two molecules were set up in the same window and the two structures were oriented following the lab script. The atoms were labelled to have the atoms on the product all match the reactant molecule.

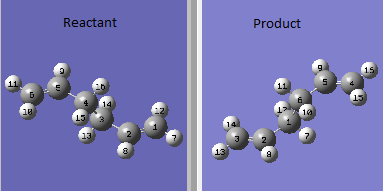
The structure was then submitted to scan for transition state optimisation and a frequency calculation was also included. The script used was shown below:

---------------------------------------------------
# opt=(calcfc,qst2) freq hf/3-21g geom=connectivity
---------------------------------------------------

However, the optimisation failed as the sturcture obtained looks more like a dissociated chair transition state. A similar imaginary vibration to the chair structure is also found at -818cm^-1, which further confirms the structure obtained is the chair transition state.

failed boat transition structure optimisation	modified structure for boat optimisation

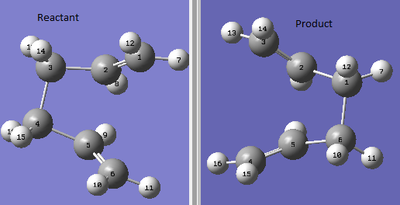
The original input file was then modified to make it look as close to the boat transition state as possible. Both the reactant and product had the central C-C-C-C- dihedral angle set to 0^o, with the inside C-C-C reduced to 100^o.

Optimisation of Boat transition state

Summary
Terminal C ends distance	2.14
Imiginary vibration at -840cm-1	click to start it
DOI	DOI:10042/to-58156

Intrinsic Reaction Coordinate (IRC) Analysis

Intrinsic Reaction Coordinate(IRC) is a method providing information on the minimum energy path from the transition structure down to its local minimum on a potential energy surface. The IRC was calculated using the optimised transition structures from the previous sections. As the reaction coordinate is symmetrical, only forward direction was chose to be computed and the force constant was calculated once with number of points along the IRC set to 50.

It was found that the IRC terminated at step 21 but it hadn't reached a minimum. The final structure obtained looks more like the structure used for the boat tranistion state optimisation. The total energy is -231.687731a.u.

IRC calculation

Resulted conformer	IRC Diagram	RMS Gradient

DOI:10042/to-58735

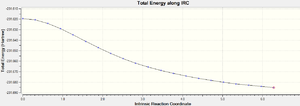Three different methods were then used to make the IRC reach a minimum geometry.

(i)Take the last step of IRC and run a normal minimisation

A normal optimisation to a minimum was set up using the final structure obtained from the previous IRC calculation. The calculation finished very fast. However, the structure obtained is the same as gauche2 with the same total energy, -231.69167 a.u and point group C₂. This indicates the chair transition structure leads to the gauche2 conformer.

(ii)Restart the IRC and set the no. of points along the IRC 100

The same result was obtained as running the IRC with the no. of points along the IRC set to 50. Therefore, this method isn't much improvement either.

(iii)Redo the IRC and compute the force constants at each step

The force constant was set to always while the other settings were kept the same as the initial IRC calculation. The results obtained has the similar total energy as the one obtained using (i), -231.69166 a.u. This is again confirms that the chair transition state leads to gauche2 conformer. This method terminates at step 47.

IRC calculation using different methods

Methods	(i)	(ii)	(iii)
Animation
Total Energy (a.u)	-231.69167	-231.68514	-231.69166
IRC Total Energy Graph
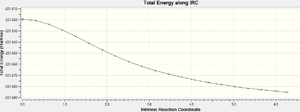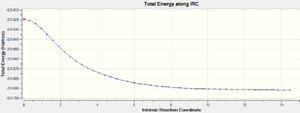
IRC RMS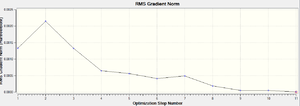
DOI	DOI:10042/to-58745	DOI:10042/to-58747	DOI:10042/to-58748

In conclusion, it is found that method (iii) could be the best choice among the three as it only requires one IRC calculation which would have reached the minimum geometry. Therefore, the IRC calculation of the boat transition state was carried out using method(iii). The structure obtained at the final step is a gauche conformer of point group C₁.

IRC calculation of boat transition state

Animation
Total Energy (a.u.)	-231.68528
IRC Total Energy Graph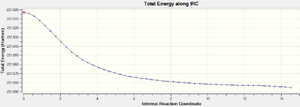
IRC RMS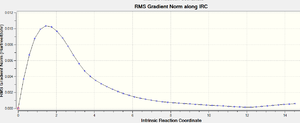
DOI	DOI:10042/to-58238

Activation Energies

Both chair and boat transition structures were optimised at B3LYP/6-31G* levle of theory using the HF/3-21G optimised structures. The activation energy is obtained by finding the difference between the reactants and transition states with the corresponding calculating methods. The methods used are listed below. Since the sum of electronic and zero-point energy at different temperatures roughly agrees, the sum was obtained from the 298.15K .log file.

Optimisation of transition states

Transition States	Optimisation Methods	Point Groups	Electronic Energy (a.u)	Sum of electronic and zero-point energies at 298.15K(a.u)	Sum of electronic and thermal energies at 0K(a.u.)	Terminal C ends distance (Å)	Activation Energies at 298.15K(kcal/mol)	Activation Energies at 0K(kcal/mol)	DOI
Reactant (anti2)	HF/3-21G	C2v	-231.69254	-231.52681	-231.53907	N/A	N/A	N/A	0K DOI:10042/to-59019 ;278.15K DOI:10042/to-59025
Reactant (anti2)	B31YP/6-31G*	C2v	-234.61171	-234.46143	-234.46877	N/A	N/A	N/A	0K DOI:10042/to-58598 ; 278.15K DOI:10042/to-58556
chair	HF/3-21G	C2h	-231.61932	-231.46132	-231.46667	2.02	41.1	45.4	278.15K DOI:10042/to-58969
chair	B31YP/6-31G*	C2h	-234.55698	-234.40901	-234.41493	1.97	32.9	33.8	278.15K DOI:10042/to-58414
boat	HF/3-21G	C2v	-231.60280	-231.44530	-231.45093	2.14	51.1	46.5	278.15K DOI:10042/to-58972
boat	B31YP/6-31G*	C2v	-234.54309	-234.39601	-234.40234	2.21	41.1	41.7	278.15KDOI:10042/to-59053

As seen in the above table, the chair transition state has a lower activation energy than the boat one, which indicates chair transition state pathway would be more favoured in the Cope rearrangement. The experimental activation enegies are 33.5±0.5cal/mol via the chair transition state and 44.7±2.0kcal/mol. The computational results using DFT/6-31G* roughly agrees with it.

Diels Alder Cycloaddition

Diels Alder reaction is a pericyclic cycloaddition, occuring between a conjugated diene and a dienophile, involving 4π electrons from the diene and 2π electrons from dienophile. The reaction is driven by the formation of two new σ bonds. An aromatic transition state of six delocalised π electrons is formed. The HOMO and LUMO of the same symmetry interacts with each other, forming two new σ orbitals, which usually have lower energies than those of the dienophiles.

Cycloaddition MO interpretation

In this section, the transition states of two π4s+π2s reaction are calculated, starting with AM1/semi-empricial level.

Diels Alder reaction between ethylene and butadiene

Cis-butadiene is the diene and ethylene is the dienophile in the Diels Alder reaction. The reaction scheme is shown below.

Diels Alder reaction between ethylene and butadiene

cis butadiene and ethylene MO symmetry determinations

Both reactants were optimised at AM1 semi-empirical level, using Gaussian09W.

Optimisation of cis-butadiene

Molecules	Total Energy (a.u)	HOMO (a.u)	LUMO (a.u)	C=C Bond Lengths (Å)	C-C Bond Length (Å)	.log
Cis-butadiene	0.048797	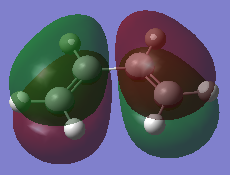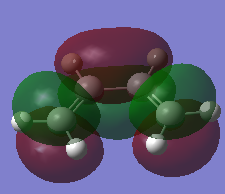-0.34381(Symmetry=a)	0.01707(Symmetry=s)	1.34	1.45	File:Hgl CISBUTADIENE OPT.LOG
Ethylene	0.02619	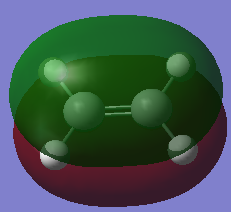-0.38775(Symmetry=s)	0.05283(Symmetry=a)	1.33	n/a	File:Hgl ethylene OPT.LOG

It can be clearly seen the LUMOs and HOMOs are formed from p-orbital overlapping, forming π bonds. The HOMO and LUMO of the diene are π₂ and π₃* orbitals respectively while the HOMO and LUMO of the ethylene are the π and π* orbitals. The HOMO of the cis-butadiene has the same symmetry as the LUMO of ethylene, both antisymmetrical whereas the LUMO of the cis-butadiene and HOMO of the ethylene are both symmetrical. Therefore, the orbitals of the same symmetry can interact with each other and the reaction is allowed. Both the HOMO and LUMO of cis-butadiene have the lower energies. Thus, the energies of new σ bond orbitals formed decreases relative to the ones of ethylene.

Transition state

The transition state was set up using the optimised cis-butadiene and ethylene structures. It was first guessed using the redundant coord editor method and was then optimised to a transition state (TS Berny) at AM1-semiexpirical level. The distance between the C atoms where the two newly formed σ bonds form was froze to 2.2Å to start the optimisation. A frequency calculation was also carried out.

Optimisation of Transition States

Methods	Freeze Coordinate (2.2Å)	Freeze Coordinate (Derivative)	TS(Berny) opt at semi-emprical/AM1
Total Energies (a.u)	0.10745	0.11166	0.11165
Point Groups	Cs	Cs	Cs
Partyly formed C-C Distance (Å)	2.20	2.12	2.12
Diene C-C Bond Length (Å)	1.42	1.40	1.40
Diene C=C Bond Length (Å)	1.36	1.38	1.38
Ethylene C=C Bond Length (Å)	1.36	1.38	1.38
DOI	DOI:10042/to-59109	DOI:10042/to-59116	DOI:10042/to-59121

At the transition state, the C=C bond of both reactants get longer as when the two new σ bonds are forming at these positions, electrons transferring from the π orbitals into the corresponding LUMO and HOMO as mentioned above. An imaginary vibration is found in the frequency analysis, which confirms the transition state has been found and π electrons transferred in a concerted stereospecific fashion.

Imiaginary and the lowest positive Vibration

wavelength (cm-1)	Animation	Description
-956		Synchronous movement of both fragments towards each other
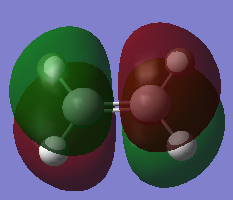
142		Synchronous rocking of both fragments

Tranistion MO Analysis

MOs	HOMO	LUMO
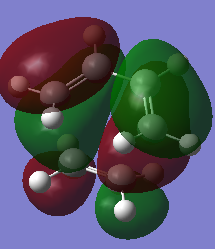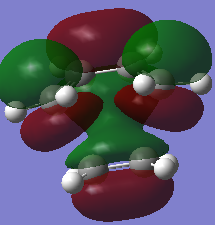MO Images	symmetry=a	symmetry=s
MO energies (a.u)	-0.32394	0.02315
Symmetries	Antisymmetric	Symmetrical

The HOMO and LUMO of the transition states agrees with the prediction mentioned at the reactants MO sections. The electrons are transferred from the π orbitals which is the HOMO of one fragment into the π* LUMO of the other fragment, forming two new σ orbitals which can be seen at the HOMO and having antisymmetric symmetry.

HOMO=HOMO(diene)+LUMO(dienophile)

LUMO=HOMO(dienophile) + LUMO(diene)

IRC

The IRC calculated at AM1/semi-emprical level further confirms the the transition state has been found. The final step structure has a symmetry of C_s.

animation of IRC

IRC energy graph

DOI:10042/to-58843

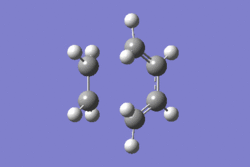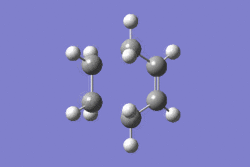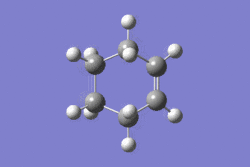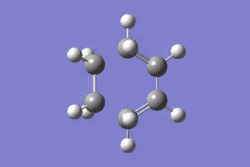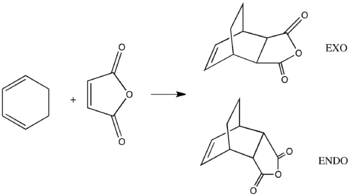
Regioselectivity of the Diels Alder Reaction between Cyclohexa-1,3-diene and maleic anhydride

The Diels Alder reaction between the cyclohexa-1,3-diene and maleic anhydride(heterodienophile) is more favoured than the Diels Alder between the cis-butadiene and ethylene due to the electronwithdrawing C=O groups in the maleic anhydride molecule, which resulted as lower energy of the LUMO. The decrease in the HOMO_(diene) and LUMO_(dienophile) gap makes the reaction more favourable. There are two possible products in the Diels Alder reaction between cyclic diene and dienophile, endo and exo adducts. In this section, the transition states formed between cyclohexa-1,3-diene and maleic anhydride were tested to study the kinetics of the reaction.

Diels Alder reaction between cyclohexa-1,3-diene and maleic anhydride

MO Analysis

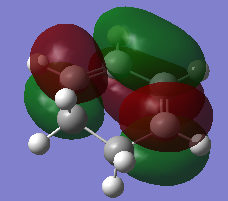
Again, both cyclohexa-1,3-diene and maleic anhydride structures were optimised at AM1 semi-empirical level before starting any transition state calculation.

Optimisation

Molecules	Total Energy (a.u.)	HOMO(a.u.)	LUMO(a.u)	.log
Cyclohexa-1,3-diene	0.02771	-0.32194(Symmetry=a)	0.01680(Symmetry=s)	DOI:10042/to-59077
Maleic Anhydride	-0.12182	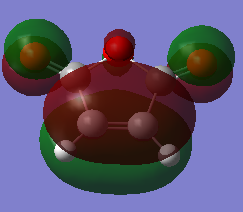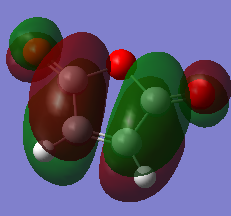-0.44187(Symmetry=s)	-0.05949(Symmetry=a)	File:Hgl MALEIC ANHYDRIDE.LOG

Both HOMO and LUMO of maleic anhydride have negative energies, resulting from the presence of more electronegative O atoms. The lowering energy of LUMO enables better orbital overlapping with the HOMO of diene.

Transition State

The transition states were set up by using the optimised maleic anhydride and cyclohexa-1,3-diene. Both structures were optimised using redundant coord editor method. The structures obtained were then optimised further using AM1/semi-emprical to TS(Berny) and frequency analysis were included as well. The partyly forming σ bonds were set to 2.2Å at the beginning of the freeze coordinate optimisation.The optimisation results are tabulated.

Transition States Optimisation

	Endo Adduct	Endo Adduct	Exo Adduct	Exo Adduct
Methods	Redundant Coor Editor	TS(Berny)	Redundant Coor Editor	TS(Berny)
Final structures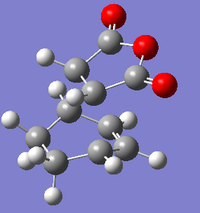
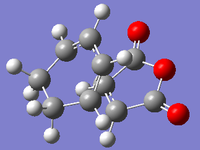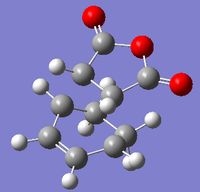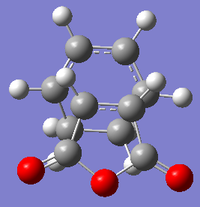
Total Energies (a.u)	-0.06945	-0.05150	-0.06959	-0.05042
Imaginary Vibration (cm-1)	n/a	-806	n/a	-812
Partly Forming σ C-C Bond Length (Å)	2.00	2.16	2.00	2.17
Diene C=C Bond (Å)	1.50	1.39	1.45	1.39
Diene C-C Bond (Å)	1.53	1.40	1.36	1.40
Anhydride C=C Bond (Å)	1.47	1.41	1.47	1.41
DOI	DOI:10042/to-58705	DOI:10042/to-58708	DOI:10042/to-58714	DOI:10042/to-58719

All the structures obtained have the same point group: C_s. By studying the imaginary vibrations of both, it is confirmed that the transition structures have been found.

Imaginary Vibration of Endo TS

Imaginary Vibration of Exo TS

Both endo and exo products were optimised at AM1/semi-emprical level. By studying into the log file, the following data can be obtained.

Summary of Energies

	Total Energy (a.u)	Sum of electronic and zero-point energies at 0K	Sum of electronic and thermal energies at 298.15K	Sum of electronic and thermal free energies(a.u.)	ΔEa at 0K(kcal/mol)	ΔEa at 298.15K(kcal)	ΔH at 0K(kcal/mol)	ΔH at 298.15K(kcal/mol)	ΔG(kcal/mol)	DOI
Maleic Anhydride	-0.05819	-0.06335	-0.05819	-0.09250	n/a	n/a	n/a	n/a	n/a	DOI:10042/to-59151
Cyclo-1,3-diene	0.02771	0.15250	0.15773	0.12449	n/a	n/a	n/a	n/a	n/a	DOI:10042/to-59152
Reactants Total	-0.03048	0.08915	0.09954	0.03199	n/a	n/a	n/a	n/a	n/a	n/a
Endo TS	-0.05150	0.13349	0.14368	0.09735	27.8	27.7	n/a	n/a	n/a	DOI:10042/to-58708
Endo Product	-0.16017	0.03146	0.04046	-0.00316	n/a	n/a	-36.2	-37.1	-22.1	DOI:10042/to-59146
Exo TS	-0.05042	0.13488	0.14488	0.09912	29.7	28.5	n/a	n/a	n/a	DOI:10042/to-58719
Exo Product	-0.15991	0.03170	0.04068	-0.00288	n/a	n/a	-36.1	-37.0	-62.9	DOI:10042/to-59147

As found in the Cope rearrangement, the results obtained using DFT/6-31g* method are more accurately. i.e. the optimisation was then carried out at DFT/6-31G* level.

Summary of Energies

	Electronic Energy	Sum of electronic and zero-point energies at 0K	Sum of electronic and thermal energies at 298.15K	Sum of electronic and thermal free energies (a.u)	ΔEa at 0K(kcal/mol)	ΔEa at 298.15K(kcal)	ΔH at 0K(kcal/mol)	ΔH at 298.15K(kcal/mol)	ΔG(a.u)	DOI
Maleic Anhydride	-379.28954	-379.23366	-379.22847	-379.26273	n/a	n/a	n/a	n/a	n/a	DOI:10042/to-59155
Cyclo-1,3-diene	-233.41891	-233.29610	-233.29092	-233.32370	n/a	n/a	n/a	n/a	n/a	DOI:10042/to-59154
Reactants Total	-612.70845	-612.52976	-612.51939	-612.58643	n/a	n/a	n/a	n/a	n/a	n/a
Endo TS	-612.68340	-612.50214	-612.49179	-612.53833	17.3	17.3	n/a	n/a	n/a	DOI:10042/to-58758
Endo Product	-612.75829	-612.57207	-612.56261	-612.60718	n/a	n/a	-26.5	-27.1	-13.0	DOI:10042/to-59157
Exo TS	-612.67931	-612.49801	-612.48766	-612.53426	19.3	19.9	n/a	n/a	n/a	DOI:10042/to-58757
Exo Product	-612.75579	-612.56938	-612.55998	-612.60428	n/a	n/a	-24.9	-25.5	-11.2	DOI:10042/to-59156

The results obtained using both methods exhibit the same trend: the endo transition state has the lower activation energy, which means the endo product is the kinetic product. i.e., the exo product is thermodynamic product. The difference between the total energies of both products are not significant, which means a mixer of the isomers could be formed from the reaction, rather than a single adduct. The difference between the electronic and thermal energies of both transition states becomes less as the temperature increases. Therefore, the preference between the two transition states would be less. The reaction via the exo transition state would be irreversibly forming the more stable exo product whereas the reaction via the endo transition state becomes reversible, converting to the exo transition state and then exo product slowly.

Bonding interaction and Secondary Orbital Overlap

The MOs of both transition states are obtained using the optimised structures at AM1/semi-empirical level.

MO Analysis

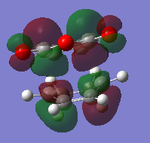
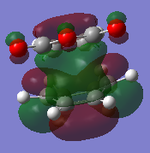
MOs	HOMO-1	HOMO	LUMO	LUMO+1	Energies
Exo Adduct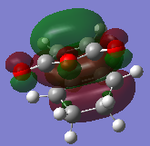
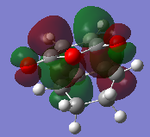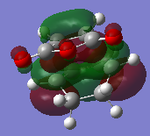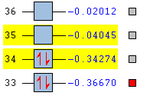
Endo Adduct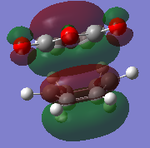

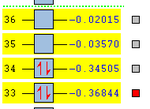
It can be clearly seen that the endo adduct MOs have lower energy than those of exo adduct. The endo transition has the lower energy as a result of secondary orbital overlap. This can be seen in the MOs of the endo adduct shown above. In addition to these, the secondary overlap of the endo transition state are also found at MO 16 and 22,which is not observed at the exo MOs.

MO 16

MO 16

MO 22

MO 22

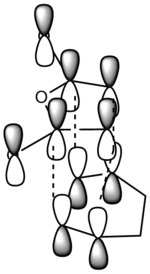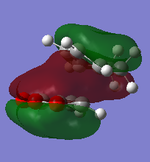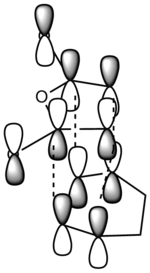IRC

The IRC were calculated using the AM1/semi-empirical optimised structures at the same level.

IRC

Transition States	Animation	IRC energy diagram	DOI
Endo			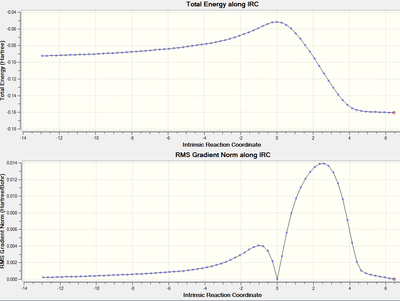DOI:10042/to-59159
Exo			DOI:10042/to-59158

As seen in the animations, the transition states of both exo and endo adduct have been found.

Over all, it is found the endo transition state is more favourable. This agrees with the Diels Alder endo rule: The one leading to the endo product was generally, though not exclusively, preferred.