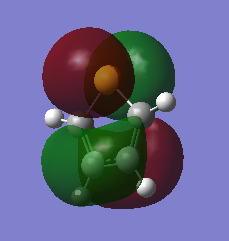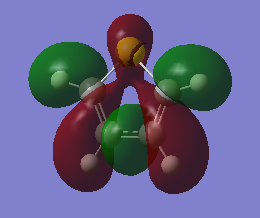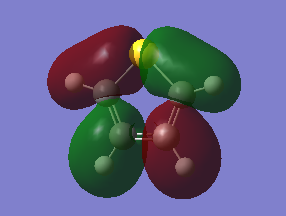Rep:Mod:heterocyclic5memberd
The aims of investigation
Investigation into Aromaticity
The criteria stated by IUPAC for aromatic compounds are the following, enhanced thermodynamic stability (energetic criteria), alternation of bond lengths in ring (structural criteria) and the presence of a diamagnetic ring current (magnetic criteria). In this project, the aim is to investigate all three criteria for three heteroaromatics by computational methods. The bond length data can be obtained from optimized structures and the population analysis. The thermodynamic stability can be probed by looking into the difference in energy of the HOMO-LUMO gap from population analysis calculations. The magnetic criteria can be probed by using the NICS method stated below.
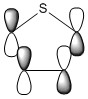
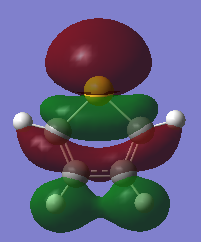
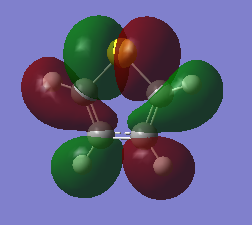
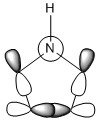
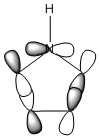
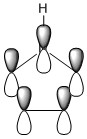
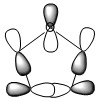
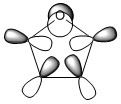
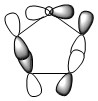
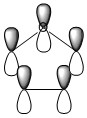
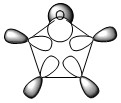
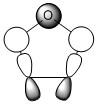
The three chosen heteroaromatics are thiphene, pyrrole and furan. These are all isoelectronic with each other. For aromatic systems such as benzene, there exists degenerate molecular orbitals which can be dictated by Musulin-Frost diagrams. For the case of five membered heteroaromatics this is not so. Thus there is expected to be no degenerate molecular orbitals.
Note: When LCAO has been used to show construction of molecular orbitals, hydrogen orbitals have often been omitted to reduce clutter
NICS
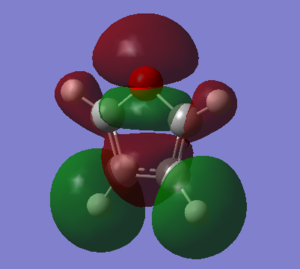
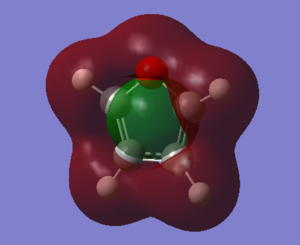
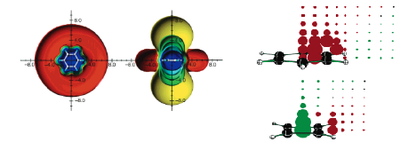
NICS (nuclear independent chemical shift) has been used as a method of determining if a molecule exhibits aromatic behaviour. This uses computed NMR chemical shifts as a way of probing the local magnetic field which is a consequence of ring current. One can do this in Gaussian by placing a ghost atom in the centre of the ring, not the centre of mass, but the spacial centre (centre of mass will cause problems with the "believed to be" heteroaromatics since one of the atoms in the ring system is a lot heavier than the other carbon atoms present). A standard procedure is to place this ghost atom in the plane of the ring, i.e. if ring lies in the xy plane, we will place the ghost atom in the centre at z=0. This is referred to as the NICS(0). The next step is to place the ghost atom at z=1, i.e. 1 angstrom in the positive z direction. The chemical shifts are then compared. We obtain the magnetic shielding value, and simply change its sign. If this value is significantly negative, it can be justified by the induced ring currents from aromaticity. If this value is positive, i.e. deshielded, it implies anti aromaticity.
NMR experiments involve an applied magnetic field. The movement of delocalised electrons in an aromatic compound induces its own magnetic field. This induced field can either align with or against the applied magnetic field, B. For the first case, centre of the molecule experiences a lesser magnetic field, where as being outside of the ring there is a greater magnetic field felt.
One can create a grid of ghost atoms that can be used to map the delocalised electron density. These studies have been carried out by Chen[1] et al. Venturing outside the area of the ring shows a value with the opposite charge, a positive value if aromatic, or a negative value if anti-aromatic.
(Note: Ghost atoms are labelled in Gaussian as Bq which stands for Banquo (from Macbeth))
Method and Basis Sets
Each heteroaromatic was optimized to an eventual MP2 6-311G+(2d,p) basis set via a step-wise process. After each successful optimization a frequency analysis was carried out to confirm the correct minimum was determined (i.e. not a transition state). Once this was confirmed the sequential optimization was executed. This was in the following order:
- Method: DFT Basis set: 6-311G(d,p)
- Method: MP2 Basis set: 6-311G(d,p)
- Method: MP2 Basis set: 6-311G+(2d,p)
The log files corresponding to the first two optimizations as well as the corresponding frequency data can be found in the supplementary section of this wiki. Due to the presence of a sulphur atom, diffuse d-orbital terms were included in the basis set. All analysis shown below was carried out at the MP2 6-311G+(2d,p) level apart from calculation of the HOMO-LUMO energy gap which was calculated using the DFT 6-311G(d,p) method. The reason for this is due to the method of MP2 itself. When carrying out the population analysis, the method fails to calculate the unoccupied orbitals at the MP2 level, instead it uses Hartree-Fock. In order to be consistent, it was deemed necessary to calculate the energy of the HOMO and LUMO with the same method.
MP - Møller–Plesset perturbation theory, this adds correlation effects for electrons (from Rayleigh–Schrödinger perturbation theory) thus improving upon the Hartree-fock method
Optimization and Frequency Analysis of the Heteroaromatics (MP2 6-311G+(2d,p))
Optimization of the Heteroaromatics (MP2 6-311G+(2d,p))
The calculation summary for every heteroatom analysed is shown below along with the corresponding log files,
| Property | Thiophene | Pyrrole | Furan |
|---|---|---|---|
| Log File | [Log] | [Log] | [Log] |
| File Name | Thiophene_OPT_6311G(DP)_mp2_2dpplusoutput | pyrrole_OPT_MP2_2dpplus_output | Furan_OPT_MP2_2dpplus_output |
| File Type | .log | .log | .log |
| Calculation Type | FOPT | FOPT | FOPT |
| Calculation Method | RMP2-FC | RMP2-FC | RMP2-FC |
| Basis Set | 6-311+G(2d,p) | 6-311+G(2d,p) | 6-311+G(2d,p) |
| Energy | -552.08874872 au. | -209.64082452 a.u. | -229.48127966 a.u. |
| RMS Gradient Norm | 0.00000031 a.u. | 0.00000149 a.u. | 0.00000326 a.u. |
| Dipole Moment | 0.6854 D | 1.9013 D | 0.8329 D |
| Point Group | CS | C1 | C1 |
| Time Taken | 13 minutes and 34.0 seconds | 20 minutes and 58.4 seconds | 19 minutes and 6.0 seconds |
| Item Table | Item Value Threshold Converged?
Maximum Force 0.000001 0.000015 YES
RMS Force 0.000000 0.000010 YES
Maximum Displacement 0.000012 0.000060 YES
RMS Displacement 0.000003 0.000040 YES
Predicted change in Energy=-7.786065D-12
Optimization completed.
-- Stationary point found.
|
Item Value Threshold Converged?
Maximum Force 0.000003 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000012 0.000060 YES
RMS Displacement 0.000005 0.000040 YES
Predicted change in Energy=-7.136477D-11
Optimization completed.
-- Stationary point found.
|
Item Value Threshold Converged?
Maximum Force 0.000007 0.000015 YES
RMS Force 0.000002 0.000010 YES
Maximum Displacement 0.000059 0.000060 YES
RMS Displacement 0.000021 0.000040 YES
Predicted change in Energy=-5.913681D-10
Optimization completed.
-- Stationary point found.
|
All of the optimizations successfully converged to a minimum value. In the following section, the frequency analysis is carried out to determine if this minimum corresponds to a trough in the potential surface and not a transition state.
Vibrational Analysis
The table below presents the low frequency data, showing that the 6 frequencies corresponding to the 3 degrees of translational and rotational motion are small and within the +/- 15 cm-1 range. The three frequencies corresponding to vibrational degrees of freedom are all positive, indicating the optimization converged to the correct minimum point.
| Species | Low Frequencies | Log Files |
|---|---|---|
| Thiophene | Low frequencies --- -0.0034 -0.0031 -0.0016 0.1294 0.1428 0.2579 Low frequencies --- 458.2975 568.9471 616.5623 |
[Log] |
| Pyrrole | Low frequencies --- -1.5731 -0.7369 0.0008 0.0009 0.0010 1.1724 Low frequencies --- 455.3110 615.3787 639.3606 |
[Log] |
| Furan | Low frequencies --- 0.0012 0.0012 0.0016 1.4946 1.9671 2.3673 Low frequencies --- 606.9745 626.3569 692.4575 |
[Log] |
One could compare the values obtained for the translational and rotational with those obtained at a lesser basis set in the supplementary section. It highlights the greater accuracy of the MP2 method and the larger 6-311G+(2d,p) basis set.
Analysis of Thiophene
The thiophene molecule was created using the pre-made template in Gaussian. The optimizations were carried out in the sequence previously stated.
Comparison of Bond Lengths with Literature Data
Values of the bond length were obtained by optimization of the thiophene molecule at the 6-311G+(2d,p) basis set using the MP2 method.
| Bond | Computational Length A | Literature[3] A | Bond | Angle (°) |
|---|---|---|---|---|
| C-S (1-5) | 1.717 | 1.717 (+- 0.004) | C-S-C | 92.1 |
| C=C (1-2) | 1.379 | 1.368 (+- 0.004) | S-C-C | 111.5 |
| C-C (2-3) | 1.417 | 1.424 (+-0.002) | C-C-C | 112.5 |
| C-H (1-6) | 1.081 | 1.071 (+- 0.015) | ||
| C-H (2-7) | 1.083 | - |
There is an exceptional correlation between the computed bond lengths with that of experimental gas phase electron diffraction. This supports the claim that the optimization of the thiophene molecule is to a satisfactory degree of accuracy. In a later section of this wiki the bond lengths are compared with the other heteroaromatics.
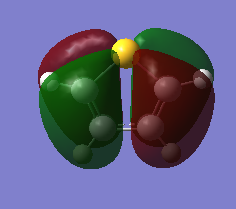
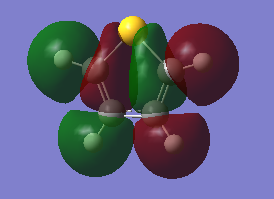
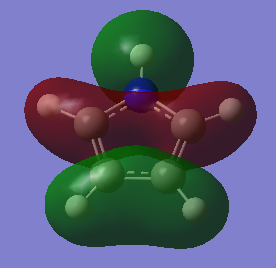
Molecular Orbitals of Thiophene
The log file can be found [here] and the checkpoint file [here]
| Molecular Orbital | Energy (a.u.) | Diagram | Comments | LCAO |
|---|---|---|---|---|
| 23 | 0.06690 (Irrelevant number due to method limitations) |  |
LUMO orbital (unfilled) relatively large HOMO-LUMO energy gap | |
| 22 | -0.32402 |  |
The p-orbitals on the carbon atoms either side of the plane through the centre of the molecule are in phase. The sulphur can either be in or out of phase, both will result in the same stabilisation energy. |  |
| 21 | -0.34606 |  |
Another π orbital showing double bond character for C-C bond opposite that of the sulphur atom. The carbon atoms have the p-orbitals in phase with each other while the sulphur p-orbital is out of phase. Two carbons have no orbitals associated with them since they can either be in phase or out of phase with respect to the sulphur atom where both combinations have the same stabilisation energy |  |
| 20 | -0.47708 |  |
The p-orbitals of the sulphur favourable interact with the orbitals on the adjacent carbon atoms. There is a through space antibonding interaction between the carbons farthest from the sulphur and that of the sulphur p-orbital. Another bonding interaction is present between the p-orbitals on the carbon atoms adjacent to the sulphur and those farthest from the sulphur |  |
| 19 | -0.52173 |  |
Fully conjugated system of in-phase p-orbitals, contributing to the aromatic behaviour. |  |
| 18 | -0.53054 |  |
All p-orbitals, carbons adjacent to heteroatom have a bonding interaction to the sulphur p-orbital. There is also a bonding interaction with the carbons adjacent to these. |  |
| 17 | -0.55475 |  |
An s-orbital on the sulphur atom that is out of phase with respect to the adjacent carbon p-orbitals resulting in a weak through space destructive interaction. The C-C atoms farthest from the heteroatom have an in-phase bonding interaction between the p-orbitals. There is also a bonding interaction between these carbon atoms and the carbons adjacent to the heteroatom. |  |
| 16 | -0.57525 |  |
Four p-orbitals on the carbon framework with phases that result in a nodal plane directly down the centre of the molecule (heteroatom to C-C bond). The sulphur can either be in-phase or out of phase giving equal interaction energies. |  |
| 15 | -0.69807 |  |
A nodal plane around the ring framework which can only be achieved by p-orbitals aligned so that the lobes point into the centre creating a stabilising interaction (p-orbitals along the C-H bonds) |  |
| 14 | -0.75216 |  |
Carbon s-orbitals are arranged out of phase, but has a bonding interaction with the p-orbital on the adjacent carbon atoms. The p-orbitals of these carbon atoms have a bonding interaction with the inphase p-orbital on sulphur |  |
| 13 | -0.76827 |  |
The sulphur atom has an s-orbital out of phase to the adjacent carbon s-orbitals. The two carbon atoms farthest from the heteroatom have p-orbitals directed along the C-C framework resulting in a bonding interaction. |  |
| 12 | -0.98209 |  |
The s-orbitals of carbon have a bonding interaction to adjacent carbon s-orbitals, there is a nodal plane directly through the centre of the molecule. The sulphur atom has a p-orbital aligned with the adjacent s-orbitals. |  |
| 11 | -0.98814 |  |
Bonding orbital of the σ-framework constructed by s-orbitals |  |
| 10 | -1.17196 |  |
The entirely bonding orbital constructed from five s-orbitals all in phase |  |
The calculation of the HOMO-LUMO energy gap shown below uses the DFT method with a 6-311G(d,p) basis set due to reasons previously stated. The log file can be found [here] and the checkpoint file [here]
| Molecular Orbital | Energy | Diagram | Comments |
|---|---|---|---|
| 23 | -0.01819 |  |
LUMO orbital (unfilled) relatively large HOMO-LUMO energy gap |
| 22 | -0.24260 |  |
A π orbital showing conjugation over the double bonds |
The HOMO-LUMO energy difference appears to be 0.22441 a.u.. This is equivalent to 6.10651 eV, this is in the range of energies associated with aromatic compounds (c.f. 6-membered aromatics have a value of 7-8 eV)
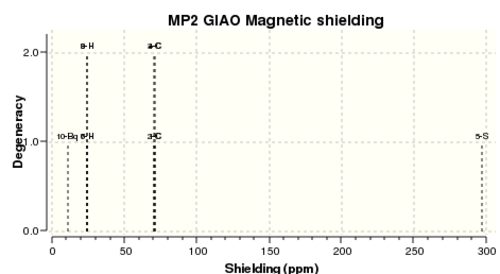
NMR Calculations (GIAO)
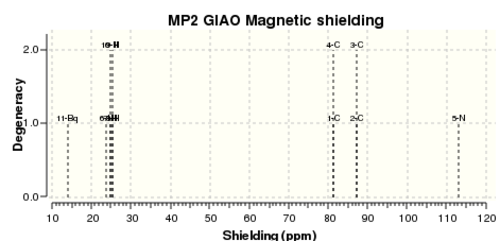
The coordinates used for placing the ghost atom to obtain NICS(0) is shown explicitly below, the same coordinates were used for calculation of NICS(1) with the only difference of the z coordinate now being equal to 1. Coordinates shall not be shown for further NMR calculations but can be viewed in the log file.
Note: GIAO stands for gauge-independent atomic orbital
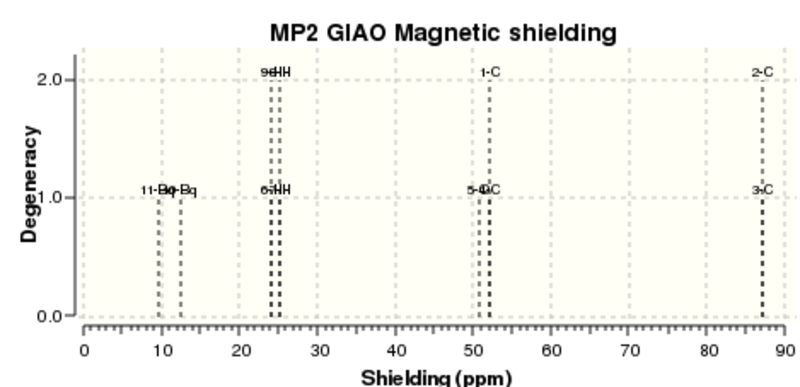
C 0. -0.00105 1.23603 C 0. -1.27459 0.70835 C 0. -1.27459 -0.70835 C 0. -0.00105 -1.23603 S 0. 1.19142 0. H 0. 0.28998 2.27671 H 0. -2.16754 1.32163 H 0. -2.16754 -1.32163 H 0. 0.28998 -2.27671 Bq 0. -0.27197 0.
The NICS(0) log file can be found [here] with the d-space file [here]
The NICS(1) log file can be found [here] the d-space file can be found [here]
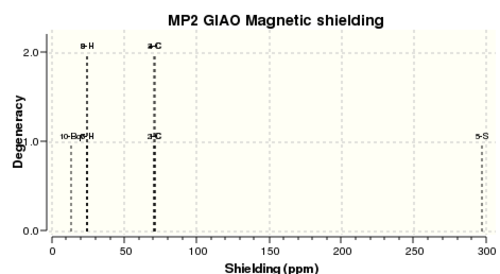
GIAO calculations to compute the degree of shielding NMR was carried out on the MP2 6-311G+(2d,p) optimization.
As seen below, taking the negative value as dictated by the method yields NICS values with a negative magnitude indicating aromaticity.
| Spectrum of GIAO NMR | |
|---|---|
| NICS(0) | NICS(1) |
 |
|
| NICS(0)= -13.5593 | NICS(1)= -10.7779 |
10 Bq Isotropic = 13.5593 Anisotropy = 7.9412 XX= 13.7879 YX= 0.0000 ZX= 0.0000 XY= 0.0000 YY= 18.8534 ZY= 0.0000 XZ= 0.0000 YZ= 0.0000 ZZ= 8.0366 Eigenvalues: 8.0366 13.7879 18.8534 |
10 Bq Isotropic = 10.7779 Anisotropy = 32.4771 XX= 32.0393 YX= -3.4502 ZX= 0.0000 XY= -3.4996 YY= 1.4616 ZY= 0.0000 XZ= 0.0000 YZ= 0.0000 ZZ= -1.1673 Eigenvalues: -1.1673 1.0717 32.4293 |
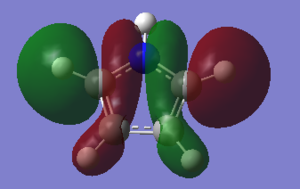
The fact that there is a difference in the shielding at two different regions in the z-direction implies there is a region of electron density above the plane of this molecule. This is what would be expected if a delocalised region of π-electrons existed here which is one of the criteria of aromaticity. Since both values show a negative value for NICS we are not dealing with anti aromaticity
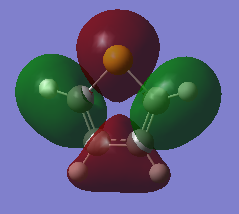
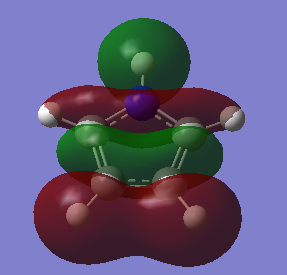
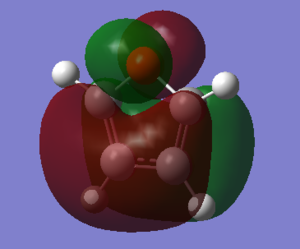
Charge Distribution and Contribution of Orbitals for Thiophene
Carbon and sulphur both have very similar electronegativities while hydrogen has a much lower value. The fact that each carbon is bonded to hydrogen results in the carbon atoms being slightly electronegative which induces this effect on the sulphur atom (reducing the valent electron density on the sulphur). Sulphur has more diffuse orbitals and is thus more easily polarised.
| Pictorial Representation of Dipole Moment | |
|---|---|
| |
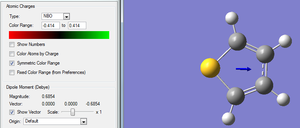
| Dipole Moment | -0.6854 D (vector) |
The dipole moment of this molecule points away from the heteroatom, indicating the net negative charge is not in sulphur region. This is further supported by the quantitative and qualitative charge distribution shown in the figures below.
| Quantitative Charge Distribution of Thiophene | |
|---|---|
| |
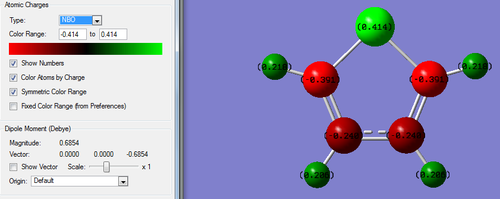
| Atom | Charge |
| S | 0.414 |
| C1 | -0.391 |
| C2 | -0.240 |
| C3 | -0.240 |
| C4 | -0.391 |
| H6 | 0.218 |
| H7 | 0.206 |
| H8 | 0.206 |
| H9 | 0.218 |
The NBO analysis of thiophene reveals information on the occupancy and hybridisation of the orbitals involved.
2. (1.88447) BD ( 2) C 1 - C 2
( 52.75%) 0.7263* C 1 s( 0.00%)p 1.00( 99.87%)d 0.00( 0.13%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.9984 0.0408 -0.0137 0.0020 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 -0.0329 0.0028 -0.0134
-0.0086 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000
( 47.25%) 0.6874* C 2 s( 0.00%)p 1.00( 99.90%)d 0.00( 0.10%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.9985 0.0396 0.0184 0.0034 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 -0.0005 0.0030 0.0320
0.0025 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000
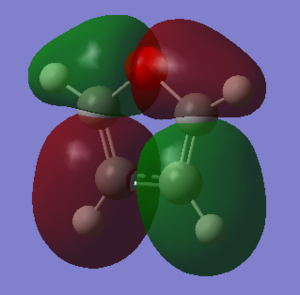
The data above shows a bonding interaction between two carbon atoms. A slightly high contribution of the orbital originates from the carbon atom closest to the heteroatom. The type of orbital contributing to this bond is almost entirely p-character, as would be expected for the aromatic system. The number of electrons in this bond is 1.88447 which is slightly less than out be expected for the 2-electron π-bond.
22. (1.66170) LP ( 2) S 5 s( 0.00%)p 1.00( 99.89%)d 0.00( 0.11%)
The sulphur lone-pair contributing to the aromaticity is almost entirely p-character, however, the number of electrons in this bond is 1.66170 which is significantly less than the expected 2-electron occupancy. The total electron count for the p-electrons appears to be 5.43064. This is less than the expected 6 electrons. It appears that this missing electron density has been transferred to the Rydberg term, this is not in the scope of this experiment.
Atom No Natural Electron Configuration
----------------------------------------------------------------------------
C 1 [core]2S( 1.04)2p( 3.32)3d( 0.01)4p( 0.02)
C 2 [core]2S( 0.95)2p( 3.26)3d( 0.01)4p( 0.02)
C 3 [core]2S( 0.95)2p( 3.26)3d( 0.01)4p( 0.02)
C 4 [core]2S( 1.04)2p( 3.32)3d( 0.01)4p( 0.02)
S 5 [core]3S( 1.59)3p( 3.93)4S( 0.01)3d( 0.04)5p( 0.02)
H 6 1S( 0.78)
H 7 1S( 0.79)
H 8 1S( 0.79)
H 9 1S( 0.78)
The natural electron configuration data above shows that the carbon atoms possess additional electron density while that of the hydrogen atoms and sulphur have fewer electrons. This data is in accordance to the calculated charge distribution of the molecule.
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
2. BD ( 2) C 1 - C 2 /164. BD*( 2) C 3 - C 4 29.34 0.52 0.115
8. BD ( 2) C 3 - C 4 /158. BD*( 2) C 1 - C 2 29.34 0.52 0.115
22. LP ( 2) S 5 /158. BD*( 2) C 1 - C 2 41.82 0.48 0.128
22. LP ( 2) S 5 /164. BD*( 2) C 3 - C 4 41.82 0.48 0.128
Analysis of Pyrrole
The same procedure as carried out for thiophene was applied to pyrrole, working through small basis sets confirming that a minimum point was found.
Comparison of Bond Lengths with Literature Data
| Bond | Computational Length A | Literature[4] A | Bond | Angle (°) |
|---|---|---|---|---|
| C-N (1-5) | 1.37 | 1.37 | C-N-C | 110.2 |
| N-H | 1.01 | - | N-C-C | 107.5 |
| C=C (1-2) | 1.38 | 1.37 | C-C-C | 107.5 |
| C-C (2-3) | 1.42 | 1.43 | ||
| C-H (1-6) | 1.09 | - | ||
| C-H (2-7) | 1.08 | - |
There is good agreement between the bond lengths from the optimization calculations to that of experimental x-ray diffraction studies. This indicates that the method and basis set used is suitable and produces results of satisfactory accuracy. The bond lengths will be compared with the other heteroaromatics in a subsequent section. The C-N-C bond angle is greater than what is observed in furan. This is a direct consequence of the difference in electronegativites between the heteroatom and the adjacent carbon atoms being less than is observed in furan.
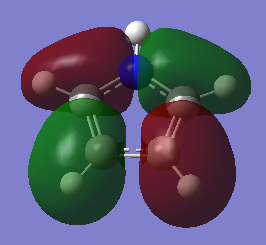
Molecular Orbitals of Pyrrole
The log file for the energy calculation using the MP2 6-311G+(2d,p) basis set can be found [here] and the checkpoint file [here] The total number of aromatic electrons in pyrrole is 5.35797
| Molecular Orbital | Energy (a.u.) | Diagram | Comments | LCAO Diagrams |
|---|---|---|---|---|
| 19 | 0.06130 (Irrelevant number due to method limitations) |  |
LUMO orbital (unfilled) relatively large HOMO-LUMO energy gap | |
| 18 | -0.29534 |  |
Four p-orbitals which has the adjacent orbitals in phase with a nodal plane running directly through the C-C bond opposite the heteroatom and the heteroatom itself. |  |
| 17 | -0.34599 |  |
Six p-orbitals with the heteroatom orbital being out of phase. Part of the aromatic orbitals, conjugation through the carbon atoms. |  |
| 16 | -0.53063 |  |
A bonding interaction between two carbon p-orbitals, Some degree of overlap of adjacent p-orbitals. Presence of through space antibonding to the nitrogen s-orbital |  |
| 15 | -0.54707 |  |
Two bonding interactions of carbon p-orbitals, some overlap with the nitrogen p-orbital resulting in bonding character, but also a degree of through space antibonding between the adjacent carbon atoms opposite the heteroatom. |  |
| 14 | -0.56526 |  |
Fully bonding arrangement of p-orbitals resulting in conjugation over the entire molecule. |  |
| 13 | -0.58465 |  |
Weak bonding interactions between s and p-orbitals of carbon atoms. |  |
| 12 | -0.59290 |  |
Two bonding overlaps down the carbon framework and a through space antibonding interaction with the nitrogen p-orbital. The other lobe of the nitrogens p-orbital has bonding character to the in phase hydrogen s-orbital |  |
| 11 | -0.73650 |  |
Five p-orbitals all inphase resulting in a nodal plane around the framework itself. |  |
| 10 | -0.76774 |  |
Two carbon s-orbitals on those farthest away from the heteroatom, two p-orbitals overlapping with a nitrogen p-orbital. |  |
| 9 | -0.79387 |  |
Carbon s-orbitals and a nitrogen p-orbital have a bonding interaction. This results in a nodal plane through the molecule |  |
| 8 | -0.97660 |  |
Two carbon s-orbitals in phase adjacent to each other and the same for the other two carbon atoms. The Nitrogen can either be in phase or out of phase. There is a nodal plane through the molecule |  |
| 7 | -1.04198 |  |
Bonding orbital of the /sigma framework with the 4 carbon s-orbitals being in phase and the nitrogen s-orbital being out of phase |  |
| 6 | -1.29170 |  |
The entirely bonding MO made up of s-orbitals all in phase |  |
The data below was obtained using the DFT method and a 6-311G(d,p) basis set. The log file for this energy calculation can be found [here] and the checkpoint file can be found [here]
| Molecular Orbital | Energy (a.u.) | Diagram | Comments |
|---|---|---|---|
| 23 | 0.03654 |  |
LUMO orbital (unfilled) relatively large HOMO-LUMO energy gap |
| 22 | -0.21241 |  |
A π orbital showing conjugation over the double bonds |
The HOMO-LUMO energy gap is found to be 0.24895 a.u.. This is the equivalent of 6.7742778 eV. Once again, this is an acceptable value for an aromatic compound.
NMR Calculations (GIAO)
The log file for the NICS(0) calculation can be found [here] and the d-space file can be found [here]. The log file for the NICS(1) calculation can be found [here] and the d-space can be found [here]
| Spectrum of GIAO NMR | |
|---|---|
| NICS(0) | NICS(1) |
 |
|
| NICS(0)= -14.1101 | NICS(1)= -10.4881 |
11 Bq Isotropic = 14.1101 Anisotropy = 2.7985 XX= 15.9758 YX= 0.0000 ZX= 0.0000 XY= 0.0000 YY= 10.6590 ZY= 0.0003 XZ= 0.0001 YZ= 0.0003 ZZ= 15.6956 Eigenvalues: 10.6590 15.6956 15.9758 |
11 Bq Isotropic = 10.4881 Anisotropy = 34.7132 XX= -2.0136 YX= 0.0074 ZX= 0.5444 XY= 0.0174 YY= -0.1498 ZY= -0.0278 XZ= -1.1340 YZ= 0.0237 ZZ= 33.6278 Eigenvalues: -2.0162 -0.1497 33.6303 |
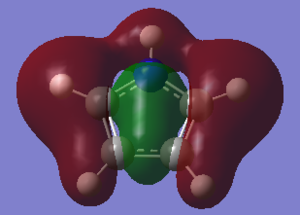
Charge Distribution and Contribution of Orbitals for Pyrrole
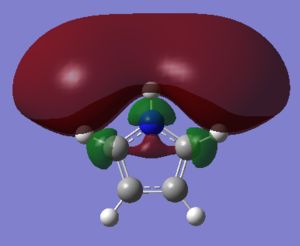
Pyrrole possesses a dipole moment that is in the opposite direction as those of pyrrole and thiophene. The vector is directed towards the nitrogen atom itself, the diagram along with the quantitative magnitude is shown in the figure below,
| Pictorial Representation of Dipole Moment | |
|---|---|
| |
| Dipole Moment | -1.9013 D (vector) |
This direction is easily explained by considering the charge distribution. It becomes apparent that the nitrogen region has a higher charge distribution (taking into account of the bonded hydrogen atom to the nitrogen) than the opposite C-C bond. The nitrogen is electronegative and thus attracts electrons. The hydrogen bonded directly too this nitrogen provides an excellent source of electrons and satisfies the nitrogens demand. Due to this, the adjacent carbon atoms do not feel the strong effect of the heteroatom and are relatively neutral species. A comparison of this behavior to that of furan is detailed in a subsequent section.
The charge density is shown in the figure below,
| Quantitative Charge Distribution of Pyrrole | |
|---|---|
| |
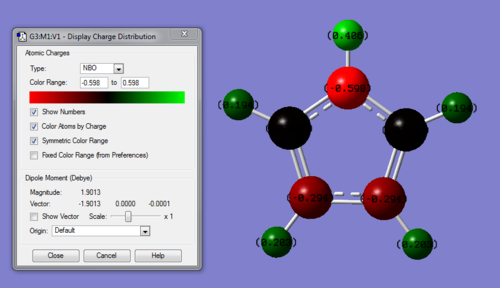
| Atom | Charge |
| N | -0.598 |
| C1 | -0.007 |
| C2 | -0.294 |
| C3 | -0.294 |
| C4 | -0.007 |
| H6 | 0.194 |
| H7 | 0.203 |
| H8 | 0.203 |
| H9 | 0.194 |
| H10 | 0.406 |
Once again the orbitals contributing to the aromaticity of the molecule are close to being of 100% p-character. This satisfies the conjugation criteria of aromaticity. As was experienced with thiophene, there is not a total electron count of 6. Once again the Rydberg term has an increased density as shown below,
2. (1.86199) BD ( 2) C 1 - C 2
( 48.68%) 0.6977* C 1 s( 0.00%)p 1.00( 99.93%)d 0.00( 0.07%)
( 51.32%) 0.7164* C 2 s( 0.00%)p 1.00( 99.89%)d 0.00( 0.11%)
8. (1.86199) BD ( 2) C 3 - C 4
( 51.32%) 0.7164* C 3 s( 0.00%)p 1.00( 99.89%)d 0.00( 0.11%)
( 48.68%) 0.6977* C 4 s( 0.00%)p 1.00( 99.93%)d 0.00( 0.07%)
18. (1.63399) LP ( 1) N 5 s( 0.00%)p 1.00( 99.99%)d 0.00( 0.01%)
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
C 1 -0.00662 1.99928 3.97544 0.03190 6.00662
C 2 -0.29367 1.99923 4.26727 0.02717 6.29367
C 3 -0.29367 1.99923 4.26727 0.02717 6.29367
C 4 -0.00662 1.99928 3.97544 0.03190 6.00662
N 5 -0.59772 1.99942 5.57358 0.02473 7.59772
H 6 0.40598 0.00000 0.59218 0.00184 0.59402
H 7 0.19355 0.00000 0.80524 0.00121 0.80645
H 8 0.20261 0.00000 0.79614 0.00125 0.79739
H 9 0.20261 0.00000 0.79614 0.00125 0.79739
H 10 0.19355 0.00000 0.80524 0.00121 0.80645
=======================================================================
* Total * 0.00000 9.99644 25.85393 0.14964 36.00000
The natural electron configuration mirrors that of the charge distribution of the molecule. That being, the electronegative nitrogen has an increased electron count than the elemental nitrogen would normally have.
Atom No Natural Electron Configuration
----------------------------------------------------------------------------
C 1 [core]2S( 0.92)2p( 3.06)3d( 0.01)4p( 0.02)
C 2 [core]2S( 0.95)2p( 3.31)3d( 0.01)4p( 0.02)
C 3 [core]2S( 0.95)2p( 3.31)3d( 0.01)4p( 0.02)
C 4 [core]2S( 0.92)2p( 3.06)3d( 0.01)4p( 0.02)
N 5 [core]2S( 1.24)2p( 4.33)3p( 0.01)3d( 0.01)
H 6 1S( 0.59)
H 7 1S( 0.81)
H 8 1S( 0.80)
H 9 1S( 0.80)
H 10 1S( 0.81)
There are several E2 energies that are particularity large. That is the donation of electrons from the C=C bond to the other resident C=C bonds π* orbital. The lonepair on the nitrogen atom is also donated into the adjacent C=C π* bonds supporting the claim of aromaticity.
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
2. BD ( 2) C 1 - C 2 /161. BD*( 2) C 3 - C 4 35.43 0.51 0.125
8. BD ( 2) C 3 - C 4 /155. BD*( 2) C 1 - C 2 35.43 0.51 0.125
18. LP ( 1) N 5 /155. BD*( 2) C 1 - C 2 62.18 0.52 0.163
18. LP ( 1) N 5 /161. BD*( 2) C 3 - C 4 62.18 0.52 0.163
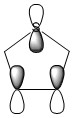
Analysis of Furan
Once again the same procedure has been used in the analysis of furan.
Comparison of Bond Lengths with Literature Data
| Bond | Computational Length A | Literature[5] A | Bond | Angle (°) |
|---|---|---|---|---|
| C-O (1-5) | 1.36 | 1.36 | C-O-C | 106.8 |
| C=C (1-2) | 1.37 | 1.36 | O-C-C | 110.4 |
| C-C (2-3) | 1.43 | 1.43 | C-C-C | 106.2 |
| C-H (1-6) | 1.08 | 1.09 | ||
| C-H (2-7) | 1.08 | 1.09 |
As can be seen from the table above, the computed bond lengths are in excellent accordance to literature values from combined analyses of electron diffraction, rotational spectroscopy and liquid crystal NMR spectroscopy. This improves the validity of the data and shows that a sufficient basis set was used.
The C=C bond length is slightly longer than a localised double bond. This implies that there is some double bond character and single bond character (single bond is longer than double bond). This is what is expected if the system is to be considered aromatic.
The C-N-C bond is relatively small compared to the case of pyrrole (110.2°). This can be explained by the electronegativity difference between oxygen and the adjacent carbon atom. This has the effect of contracting the orbitals forcing the bonds closer together.
Molecular Orbitals of Furan
The log file for the energy calculation using the MP2 method and the 6-311G+(2d,p) basis set can be found [here] and the checkpoint file [here]
| Molecular Orbital | Energy (a.u.) | Diagram | Comments | LCAO |
|---|---|---|---|---|
| 19 | 0.06893 (Irrelevant number due to method limitations) |  |
LUMO orbital (unfilled) relatively large HOMO-LUMO energy gap | |
| 18 | -0.31824 |  |
There is a nodal plane directly through the centre of the molecule resulting from two adjacent carbons p-orbitals overlapping, forming a double bond. The oxygen atom can adopt either of the phases with no difference in energy between the two. |  |
| 17 | -0.39811 |  |
All carbon p-orbitals are inphase resulting in conjugation between these orbitals. The p-orbital of the oxygen atom is out of phase |  |
| 16 | -0.54278 |  |
All carbon p-orbitals are arranged to yield a bonding interaction. The p-orbital on the oxygen also contributes to bonding character by an inphase overlap. |  |
| 15 | -0.56918 |  |
The p-orbital of the oxygen atom has constructive overlap with the adjacent carbon p-orbitals. The p-orbitals on the carbon atoms farthest from the heteroatom have a destructive overlap with the orbitals previously mentioned. |  |
| 14 | -0.57717 |  |
There is a nodal plane directly down the centre of the molecule. There is also a significant bonding interaction between the p-orbital of the oxygen atom to the p-orbitals of the adjacent carbon atoms. The carbon atoms farthest from the heteroatom contribute bonding character to the carbons adjacent to the heteroatom, this results in the centre of the molecule having a bond in phase and out of phase density. |  |
| 13 | -0.61163 |  |
A bonding interaction between the p-orbital on the oxygen atom and the p-orbitals on the adjacent carbon atoms. These adjacent carbon atoms each have a lobe resulting in a bonding interaction to a carbon s-orbital. There is a nodal plane down the centre of the molecule |  |
| 12 | -0.63203 |  |
Five p-orbitals all in phase resulting in a conjugated system, part of the aromatic character. |  |
| 11 | -0.74068 |  |
Five p-orbitals are all inphase each with a lobe directed to the centre of the molecule resulting in an encircled region of density. |  |
| 10 | -0.78338 |  |
The s-orbital on the oxygen atom is out of phase with respect to the adjacent carbon s-orbitals. These adjacent s-orbitals each have a bonding interaction with a carbon p-orbital. |  |
| 9 | -0.80821 |  |
There is a node on the carbon atoms adjacent to the heteroatom which implies the presence of a p-orbital. This p-orbital has a bonding interaction with the s-orbitals on the carbon atoms opposite that of the heteroatom. The p-orbital of oxygen is also bonding with the lobes of the adjacent p-orbitals. There is a nodal plane directly through the centre of this molecule and another perpendicular to this. |  |
| 8 | -1.00477 |  |
A nodal plane running directly through the centre of the molecule, the p-orbital on oxygen has a bonding interaction with the adjacent s-orbitals. |  |
| 7 | -1.08584 |  |
The s-orbitals on the carbon atoms are all in-phase while the s-orbital on the oxygen is out of phase |  |
| 6 | -1.45933 |  |
The entirely bonding orbital constructed from s-orbitals which are all in phase |  |
The data below was obtained using the DFT method and the 6-311G(d,p) basis set. The log file can be found [here] and the formatted checkpoint file [here]
| Molecular Orbital | Energy (a.u.) | Diagram | Comments |
|---|---|---|---|
| 23 | 0.00673 |  |
LUMO orbital (unfilled) relatively large HOMO-LUMO energy gap |
| 22 | -0.23477 |  |
A π orbital showing conjugation over the double bonds |
The HOMO-LUMO energy gap is found to be 0.24150 a.u.. This is equivalent to 6.5715529 eV which is in the acceptable range for an aromatic compound.
NMR Calculations (GIAO)
The d-space file can be found [here] and the log file can be found [here] both of these have the combined calculations of NICS(0) and NICS(1)
| Spectrum of GIAO NMR | |
|---|---|
| NICS(0) and NICS(1) | |
| |
| NICS(0)= -12.4470 | NICS(1)= -9.7412 |
10 Bq Isotropic = 12.4470 Anisotropy = 6.5902
XX= 8.2817 YX= 0.0000 ZX= 0.0001
XY= 0.0000 YY= 16.8405 ZY= -0.0003
XZ= 0.0000 YZ= -0.0003 ZZ= 12.2189
Eigenvalues: 8.2817 12.2189 16.8405
|
11 Bq Isotropic = 9.7412 Anisotropy = 30.2277 XX= 1.8452 YX= -0.0385 ZX= -0.0474 XY= -0.0242 YY= -2.4564 ZY= 1.0463 XZ= 0.0635 YZ= 1.7012 ZZ= 29.8346 Eigenvalues: -2.5149 1.8454 29.8930 |
Note: 10 Bq corresponds to the plane of the ring, 11 Bq is 1 A from this centre
Charge Distribution and Contribution of Orbitals for Furan
There is an overall dipole on the furan molecule orientated away from the oxygen atom. This is shown with the corresponding magnitude in the figure below,
| Pictorial Representation of Dipole Moment | |
|---|---|
| |
| Dipole Moment | -0.8329 D (vector) |
This direction may seem counter-intuitive. The vector for the dipole moment points from positive charge to negative by convention. With oxygen being highly electronegative, it may seem initially obvious that the region of the molecule containing oxygen will be the negative region thus expecting the vector to point towards the oxygen. However this is not the full picture! By considering the charge distribution shown in the pictures below, the carbon atoms in the C-C bond opposite to the oxygen houses a significant amount of charge, and when summed results in a greater distribution of negative charge than that of the charge in oxygen, hence the direction of the vector.
| Quantitative Charge Distribution of Furan | |
|---|---|
| |
| Atom | Charge |
| O | -0.555 |
| C1 | 0.185 |
| C2 | -0.305 |
| C3 | -0.305 |
| C4 | 0.185 |
| H6 | 0.187 |
| H7 | 0.211 |
| H8 | 0.211 |
| H9 | 0.187 |
The electronegativity of oxygen results in this atom having an increased electron density, gaining the density from the adjacent carbon atoms. This is further backed up in the natural electron configuration shown below. It is apparent that the oxygen atom has 6.56 electrons when the element itself should contribute 6 electrons. Two of the carbon atoms have 3.81 electrons each, thus they are short of electrons, and further supporting the inductive withdraw of electrons towards the oxygen atom. The two carbon atoms farthest from the oxygen atom experience an increase in electron density, this is partially from the electropositive adjacent carbons and also from the bonded hydrogen atoms.
Atom No Natural Electron Configuration
----------------------------------------------------------------------------
C 1 [core]2S( 0.93)2p( 2.86)3d( 0.01)4p( 0.02)
C 2 [core]2S( 0.97)2p( 3.31)3d( 0.01)4p( 0.01)
C 3 [core]2S( 0.97)2p( 3.31)3d( 0.01)4p( 0.01)
C 4 [core]2S( 0.93)2p( 2.86)3d( 0.01)4p( 0.02)
O 5 [core]2S( 1.60)2p( 4.93)3p( 0.01)3d( 0.02)
H 6 1S( 0.81)
H 7 1S( 0.79)
H 8 1S( 0.79)
H 9 1S( 0.81)
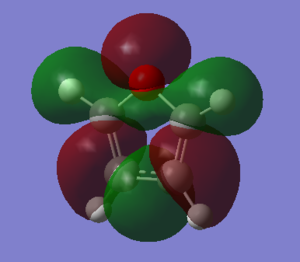
There are two lone pairs on the oxygen atom. One of which has approximately 100% p-character, this is the pair that is expected to be involved in the delocalised cloud. This statement is further validated by the E2 energy showing significant donation of the lone pair into the adjacent C-C bonds. These C-C bonds (adjacent to the oxygen) also donate electron density to each other as indicated by the E2 value. The other electron pair occupies a sp2 orbital and the E2 energy (looking at donation of electron density into accept orbitals) shows little to no behaviour, thus not involved in the overall delocalisation.
2. (1.89684) BD ( 2) C 1 - C 2
( 47.95%) 0.6925* C 1 s( 0.00%)p 1.00( 99.89%)d 0.00( 0.11%)
( 52.05%) 0.7215* C 2 s( 0.00%)p 1.00( 99.84%)d 0.00( 0.16%)
8. (1.89684) BD ( 2) C 3 - C 4
( 52.05%) 0.7215* C 3 s( 0.00%)p 1.00( 99.84%)d 0.00( 0.16%)
( 47.95%) 0.6925* C 4 s( 0.00%)p 1.00( 99.89%)d 0.00( 0.11%)
17. (1.97694) LP ( 1) O 5 s( 35.35%)p 1.83( 64.52%)d 0.00( 0.14%)
18. (1.76545) LP ( 2) O 5 s( 0.00%)p 1.00( 99.81%)d 0.00( 0.19%)
The requirement for overlapping of p-orbitals is shown to have been met in the near 100% p-character orbitals situated on the carbon atoms (each of which contains 1 electron) and the parallel p-orbital on the oxygen (contributing 2 electrons).
The requirement of 4n +2 electrons is not necessarily clear. The calculation suggests less than 6 electrons (5.55913 electrons in aromatic system), a non-integer number. This is not possible. The calculation has put electron density into the Rydberg term which is beyond the scope of this investigation. It is thus reasonable to assume that n=1 and thus we have the required 6 electrons.
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
C 1 0.18513 1.99914 3.78447 0.03126 5.81487
C 2 -0.30531 1.99921 4.27989 0.02621 6.30531
C 3 -0.30531 1.99921 4.27989 0.02621 6.30531
C 4 0.18513 1.99914 3.78447 0.03126 5.81487
O 5 -0.55513 1.99975 6.52538 0.03000 8.55513
H 6 0.18704 0.00000 0.81181 0.00114 0.81296
H 7 0.21070 0.00000 0.78803 0.00126 0.78930
H 8 0.21070 0.00000 0.78803 0.00126 0.78930
H 9 0.18704 0.00000 0.81181 0.00114 0.81296
=======================================================================
* Total * 0.00000 9.99646 25.85380 0.14974 36.00000
The E2 values that have an energy higher than 20 kcal/mol are shown below. This indicated that there is significant donation of the oxygen lonepair into the adjacent C=C π* bond as well as C=C to C=C π* donation.
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
2. BD ( 2) C 1 - C 2 /156. BD*( 2) C 3 - C 4 27.88 0.54 0.113
8. BD ( 2) C 3 - C 4 /150. BD*( 2) C 1 - C 2 27.88 0.54 0.113
18. LP ( 2) O 5 /150. BD*( 2) C 1 - C 2 42.38 0.66 0.150
18. LP ( 2) O 5 /156. BD*( 2) C 3 - C 4 42.38 0.66 0.150
Comparison of NICS Values
| Species | NICS(0) (ppm) | NICS(1) (ppm) | C-X (1-5) (A) | C=C (1-2) (A) | C-C (2-3) (A) | E2 LP to C=C (kcal/mol) | E2 C=C to C=C (kcal/mol) | Energies of Aromatic MOs | HOMO-LUMO (a.u.) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Thiophene | -13.5593 | -10.7779 | - | 1.717 | 1.379 | 1.417 | - | 41.82 | 29.34 | -0.52173, -0.34606 , -0.32402 | 0.22441 |
| Pyrrole | -14.1101 | -10.4881 | - | 1.372 | 1.384 | 1.419 | - | 62.18 | 35.43 | -0.56526, -0.34599, -0.29534 | 0.24895 |
| Furan | -12.447 | -9.7412 | - | 1.363 | 1.366 | 1.429 | - | 42.38 | 37.88 | -0.63203, -0.39811, -0.31824 | 0.24150 |
Significance of the NICS Values
The most important feature of the obtained values is a) we have a value in roughly the same order of magnitude and b) the sign of this value. The magnitude determines if there is electron density above the plane of the molecule, the sign determines if this is aromatic or anti-aromatic. Since all values above are negative, we have aromatic systems in all cases. The validity of the NICS(0) measurement in this case is debatable. This is due to the relatively small rings and thus being in the same plane as the ring may have unaccountable density from the sigma bonds (so called sigma aromaticity) and other proximity effects. By going to a distance 1 A from the ring we reduce some of this uncertainty and get a clearer picture of the true aromaticity.
This sigma-aromaticity could quite possibly be the reason for the observed high shielding value for pyrrole at NICS(0). The nitrogen orbitals has the best overlap with the carbon orbitals out of all the heteroatoms used (primarily due to the electronegativity difference and the fact they are in the same row) and so a strong sigma framework. Moving out of this region to NICS(1) there is an observed decrease in the shielding further supporting the claim that NICS(0) may not be entirely valid for these five-membered heteroaromatics.
The NICS(1) data above suggests that thiophene is the largest degree of aromaticity, followed by pyrrole and then by furan. This trend follows that of the electronegativity difference, i.e. least electronegative (thiophene) has more electron density above the molecule. Below shows the comparison of the calculated data to literature. It is important to note that the literature data was obtained using a B3LYP/6-311G* basis set. This is a lesser method and a poorer basis set since no d-orbitals have been considered. However a loose comparison can aide in showing similar trends and hence, increasing the validity of the data obtained.
| Comparison of NICS Values with Literature | ||||
|---|---|---|---|---|
| Species | Experimental (ppm) | Literature[6] (ppm) | ||
| NICS(0) | NICS(1) | NICS(0) | NICS(1) | |
| Thiophene | -13.6 | -10.8 | -13.8 | -10.8 |
| Pyrrole | -14.1 | -10.5 | -14.9 | -10.6 |
| Furan | -12.4 | -9.7 | -12.3 | -9.40 |
Significance of the HOMO-LUMO Energy Gap
One would be wrong in trying to draw trends between the HOMO-LUMO energy difference and the values obtained from the NICS calculations. These quantities are not directly related. One of the criterion of aromaticity is a large stabilization. In general this is not related to the magnetic properties associated with ring current.
The size of these values all suggest aromaticity being present. The stabilisation is largest for that of pyrrole, followed by furan and then thiophene. Once again, consideration of sulphurs diffuse orbitals can be a possible reason for the low value of the HOMO-LUMO energy gap. Since sulphurs orbitals are much more diffuse, the HOMO appears higher in energy due to less compact MOs whereas the LUMO appears lower in energy because of the weaker anti-bonding character due to poorer overlap.
Comparison of Molecular Orbitals
| MO# Pyrrole | Diagram | MO# Furan | Diagram | MO# Thiophene | Diagram | Key Differences |
|---|---|---|---|---|---|---|
| 9 | |
10 | |
13 | |
The nitrogen has significant smearing of the central density. The presence of the hetero-H bond in pyrrole results in a greater density at the top of the molecule. This is similar to that of thiophene due to the diffuse 3s orbital. The elecronegativity of oxygen has a small contracted region of density around it. |
| 10 | |
9 | |
14 | |
These orbitals are relatively equal in appearence. This is due to the hydrogen on the nitrogen only having the possibility of an s-orbital, thus in this MO the stabilisation is equal if this s-orbital was to be in or out of phase. |
| 12 | |
15 | |
17 | |
Both pyrrole and furan have a similar appearance of the molecular orbitals but for thiophene there is a discrepancy. Instead of the heteroatom using a p-orbital in bonding it uses an s-orbital. Instead of the carbon p-orbitals directing into the centre of the ring, the carbon atoms adjacent to the sulphur have the p-orbitals directed along the ring framework towards the adjacent carbon atoms. This reduces the antibonding overlap between diffuse sulphur orbital and that or the adjacent carbon p-orbitals. |
| 14 | |
12 | |
19 | |
This entirely bonding orbital constructed from parallel in-phase p-orbitals is similar for the range of heteroaromatics. Some subtle differences that manifest is that the MO for pyrrole is extended farther over the heteroatom due to the presence of the inphase overlap with the hydrogen s-orbital. The case for furan is the opposite, there is lesser electron density above the heteroatom due to no additional bond, electronegativity arguments can also be employed to explain the slightly contracted nature. For thiophene there is a similar spread to that of pyrrole due to the more diffuse orbitals. See conclusion section for thoughts on further study that came to interest when looking at this molecular orbital |
| 15 | |
14 | |
18 | |
The observation that stands out the most for these orbitals is that of the difference in the electron density in the ring region. For sulphur, there is less density in the central region as a result of the large p-orbitals on the sulphur. As a consequence of this, there is change in orientation of the p-orbital on the carbon adjacent to the sulphur atom in order to achieve greater overlap. |
The energy of the HOMO-LUMO gap can be compared with the non-cyclic fragments in order to see if there is a change in the energy from going from a linear chain to the cyclic system. If there is a change, i.e. the cyclic case has a much larger difference in energy between the HOMO and LUMO orbitals then this implies aromatic behaviour. If the opposite is true, i.e. the HOMO-LUMO gap energy is smaller for the cyclic system than for the chain, then we have anti-aromaticity.
Comparison and explanation of the ordering of the molecular orbitals of pyrrole and furan was useful in-order to probe the effects of having a hydrogen in place of a lone pair:
The molecular orbitals 6-8 are of the same ordering both molecules, the hydrogen on the nitrogen this case is in phase with the p-orbital on the nitrogen. The arrangement for orbitals 9 and 10 are reversed. The reason for this is due to orbital overlap, thus stabilization energy. For pyrrole, the s-orbital on the nitrogen has a favourable overlap with the s-orbital on directly bound hydrogen, much more stabilizing than the poorer overlap of the orthogonal p-orbital in MO 10. The furan oxygen does not have the possibility of having this bonding overlap and in this case the through space bonding wins out.
The MOs of 11 are of the same combination of LCAOs. The 12th MO of pyrrole is similar to the 15th. The reason for this re-ordering is once again due to the favourable overlap of the nitrogens p-orbital with the bound hydrogen which is not present in furan. This has good directional overlap it lying lower in energy.
In both molecules, the 13th are the same, this is because in pyrrole, the hydrogen has no orbital associated with it and thus the interactions are similar.
The 14th MO of pyrrole is paired with the 12th orbital in furan. The fact that this orbital is contracted for furan may be the reason for its stability.
The 15th MO of pyrrole corresponds to the 14th orbital of furan.
The 16th MO of pyrrole is similar to that of the 16th in furan, a difference being the orientation of the carbon p-orbitals and the degree of mixing.
From 17-18, the MOs are similar with the key difference being the presence of the hydrogen atom which is bonding and has no orbital assigned respectively.
Comparison of Bond Lengths
The difference in bond length between furan and pyrrole is not particularly large but the observed trend can be explained.
The S-C bond is the longest in the table above. This is expected since sulphur is in a different row of the periodic table and has a different principle quantum number n. This has the effect of using more diffuse orbitals to form bonds thus a poorer energy match of orbitals and therefore a longer bond. The N-C bond is not as short as the O-C bond. This can be explained in terms of the distribution of charge. There is a larger difference in the charge between oxygen and its adjacent carbon atoms than that of nitrogen and its adjacent carbon atoms. This results in a stronger attraction, forcing the nuclei closer together.
It was previously stated that furan holds onto its electrons more strongly and thus less donation into the adjacent π* bond hence the smaller C=C bond length is observed for furan. For thiophene, there is poorer orbital overlap which results in the donation of the lone pair into the π* orbital of the C=C bond less efficient than that or pyrrole. As a result of this, the bond length of C=C for thiophene is smaller than that of pyrrole.
For the C-C bond on the other hand, since we are dealing with aromatic systems, there is a resonance form associated where this C-C has double bond character. This double bond character of the C-C bond is expected to be greater for a system that has larger quantitative aromaticity. Using this argument it is evident that since pyrrole has a higher degree of delocalised lone pair character, it shows a larger degree of aromaticity and thus a shorter bond length. There is the possibility of geometric factors also manifesting, for example, decreasing the length of one bond (say the C=C) will result in an increase in another bond (C-C).
Comparison of the E2 Values
The E2 values for the donation of the lonepair into the adjacent C=C bond is larger for pyrrole (62.18 kcal/mol) than for furan (42.38 kcal/mol). The donation is into an antibonding orbital (indicated by BD*), thus the more electron density that is donated, the longer the bond is expected to be. The large difference is attributed to the electronegativity of the oxygen, resulting is less favourable donation of electron density than for that of nitrogen
Thiophene has a value of 41.82 kcal/mol, the reason for this relatively low number is once again due to the size of the orbitals and the corresponding overlap. A smaller overlap corresponds to poorer donation of charge density.
The values for donation from C=C to C=C is largest for pyrrole (35.43 kcal/mol). This value compared to furan (27.88 kcal/mol) is what should be expected when considering electronegativities. Since oxygen is more electronegative than nitrogen the electron density is held more tightly in furan than in pyrrole. Once again thiophene (29.34 kcal/mol) has a smaller value for this C=C to C=C donation than that of pyrrole. This indicates that there is less conjugation around the ring due to a more diffuse MO.
Conclusions
This experiment was successful in probing the aromatic behaviour of the three heteroaromatics. A key result was that there is not one factor that dictates how aromatic a compound actually is. It is dependent upon stabilisation energies, the degree of magnetic ring current present, and geometric factors combined. The experiment highlights the vast amount of information that can be obtained for a system, showing how computational chemistry can work complimentary to synthetic work. Thiophene proved to have the largest delocalisation of electron density above the ring, followed by pyrrole and then by furan. The electronegativity of oxygen suppresses the aromatic behaviour relative to that of nitrogen.
The method adopted and the basis set used to carry out the bulk of the analysis produced highly accurate results that were in excellent correspondence to the cited literature. This experiment can be continued to produce a contour map of the heteroaromatics, like the ones displayed for 6-membered rings by Chen et al. And also extended to look into how these heteroatoms react. Another investigation could be into changing the atom that the nitrogen in pyrrole is bonded to, for example from a hydrogen, to a methyl or even a dimer. One could probe how this electron density is spread over the ring systems.
Further investigation could be into looking at properties associated with aromaticity of porphyrins which occur widely in the biological field. These molecules are a lot larger than the simple five-membered species investigated in experiment and greater computational power would be required. Probing the effects of quadrupole moments on π-stacking of aromatic systems. The electron density above the plane of one ring can induce a quadrupole moment on an adjacent aromatic molecule.
Future Work
Another area that lies in particular interest to myself is using computational methods to explain and understand catalytic behaviour. This includes computational design of surface catalysts. As an undergraduate, there has not been much exposure to computational chemistry or catalysis for that matter beyond this lab which is what sparks my interest.
References
- ↑ Z. Chen; C. Wannere; C. Corminboeuf, Chem. Rev., 2005, 105 3842-3888, [DOI]
- ↑ Z. Chen; C. Wannere; C. Corminboeuf, Chem. Rev., 2005, 105 3842-3888, [DOI]
- ↑ W. Harshbarger; S. Bauer, Acta Cryst, 1970, B26 1010-1020, [DOI]
- ↑ M. Dewar; G. Gleicher, J. Chem. Phys., 1966, 44 759, [DOI]
- ↑ P. Liescheski; D. Rankin, J. Mol. Struct., 1989, 196, 1-19, [[1]]
- ↑ E. Pittman, Thesis, 2008, 105 , [DOI]
Supplementary information
Optimization of Thiophene(6-311G DFT)
This optimization was initially carried out as quick check as to whether the optimization gave realistic bond lengths. The calculation summary is shown in the table below, the log file can be found [here]
| Property | Value |
|---|---|
| File Name | Thiophene_opt_6311G(d,p) |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-311G(d,p) |
| Energy | -553.06968731 a.u. |
| RMS Gradient Norm | 0.00000102 a.u. |
| Dipole Moment | 0.5580 D |
| Point Group | C1 |
| Time Taken | 10 minutes and 32.1 seconds |
Item Value Threshold Converged?
Maximum Force 0.000002 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000044 0.000060 YES
RMS Displacement 0.000010 0.000040 YES
Predicted change in Energy=-1.091488D-10
Optimization completed.
-- Stationary point found.
Vibrational Analysis (6-311G (d,p)) The frequency analysis of the optimized file above was computed in order to determine if the molecule is at a minimum, i.e. no negative frequencies
The table below shows the 6 frequencies (relating to 3 translational and 3 rotational degrees of freedom) are sufficiently low, less than +/- 15 cm-1.
Low frequencies --- -5.8993 -5.0845 -2.7282 -0.0024 -0.0024 -0.0021 Low frequencies --- 453.6607 572.4653 613.8270
No further analysis using this basis set shall be made, a larger basis set and a different method shall be used.
Optimization of Thiophene using MP2 method
The MP2 method was used with a basis set of 6-311G with d and p orbitals used. The keyword opt=tight was also used. The log file can be found [here]
The calculation summary table is shown below,
| Property | Value |
|---|---|
| File Name | Thiophene_OPT_6311G(DP)_mp2 |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RMP2-FC |
| Basis Set | 6-311G(d,p) |
| Energy | -552.03715084 a.u. |
| RMS Gradient Norm | 0.00000221 a.u. |
| Dipole Moment | 0.6966 D |
| Point Group | C1 |
| Time Taken | 7 minutes and 11.6 seconds |
The item file is shown below indicating that the optimization converged.
Item Value Threshold Converged? Maximum Force 0.000005 0.000015 YES RMS Force 0.000002 0.000010 YES Maximum Displacement 0.000029 0.000060 YES RMS Displacement 0.000012 0.000040 YES Predicted change in Energy=-1.998595D-10 Optimization completed.
Vibrational Analysis
The vibrational analysis of the molecule optimized above was performed. The log file for this calculation can be found [here]
The values for the 6 low frequency vibrations are very small and all of the vibrational frequencies are positive thus we are at the correct minimum.
Low frequencies --- 0.0017 0.0026 0.0038 0.4122 0.4539 0.4760 Low frequencies --- 444.7068 518.0811 624.6835
Once again this is not the desired end point of the optimization. It is suggested that using the basis set of 6-311G+(2d,p) will result in a satisfactory degree of accuracy.
Optimization of Pyrrole (DFT 6-311G)
The log file can be found [here]. The summary of the calculation is shown in the table below
| Property | Value |
|---|---|
| File Name | pyrrole_opt_6311gdp |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-311G(d,p) |
| Energy | -210.22608145 a.u. |
| RMS Gradient Norm | 0.00000105 a.u. |
| Dipole Moment | 1.9413 D |
| Point Group | C1 |
| Time Taken | 9 minutes and 31.6 seconds |
As can be seen below, the optimization has converged successfully to a value.
Item Value Threshold Converged?
Maximum Force 0.000002 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000053 0.000060 YES
RMS Displacement 0.000013 0.000040 YES
Predicted change in Energy=-8.775769D-11
Optimization completed.
-- Stationary point found.
Vibrational Analysis Using the optimized file above, the frequency of the molecule was analysed to determine whether a minimum was found. The log file can be found [here]
It is evident from the data below that the calculation has converged to the correct minimum as the frequencies corresponding to vibrations are positive. The frequencies corresponding to translation and rotational motion are also small and within the range of acceptance.
Low frequencies --- -3.3032 -0.0007 -0.0005 -0.0005 5.1258 6.2566 Low frequencies --- 471.6446 630.8539 640.6732
Optimization of Pyrrole (MP2 6-311G(d,p))
The log file for this optimization can be found [here]. The table below shows the Gaussian calculation summary information,
| Property | Value |
|---|---|
| File Name | Pyrrole_OPT_MP2_output |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RMP2-FC |
| Basis Set | 6-311G(d,p) |
| Energy | -209.59374602 a.u. |
| RMS Gradient Norm | 0.00000108 a.u. |
| Dipole Moment | 1.9742 D |
| Point Group | C1 |
| Time Taken | 6 minutes and 37.3 seconds |
The optimization was successful in converging to a value as highlighted below,
Item Value Threshold Converged?
Maximum Force 0.000001 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000023 0.000060 YES
RMS Displacement 0.000007 0.000040 YES
Predicted change in Energy=-5.998088D-11
Optimization completed.
-- Stationary point found.
Vibrational Analysis The log files for this calculation can be found [here]. The optimization was correct in finding the minimum point as highlighted by the table below,
Low frequencies --- -3.3032 -0.0007 -0.0005 -0.0005 5.1258 6.2566 Low frequencies --- 471.6446 630.8539 640.6732
Optimization of Furan (DFT 6-311G(d,p)
The initial optimization log file can be found [here]. The calculation summary for the optimization is shown in the table below,
| Property | Value |
|---|---|
| File Name | Furan_OPT_6311gdp |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-311G(d,p) |
| Energy | -230.08341163 a.u. |
| RMS Gradient Norm | 0.00000154 a.u. |
| Dipole Moment | 0.6222 D |
| Point Group | C1 |
| Time Taken | 10 minutes and 32.2 seconds |
The optimization was successful in converging to a value,
Item Value Threshold Converged?
Maximum Force 0.000004 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000011 0.000060 YES
RMS Displacement 0.000004 0.000040 YES
Predicted change in Energy=-6.947823D-11
Optimization completed.
-- Stationary point found.
Vibrational Analysis The frequency was calculated using the optimized file above in order to determine if the system has converged to the correct minimum. The log file can be found [here]
As hoped, the correct minimum point has been found as indicated by the positive vibrational frequencies
Low frequencies --- -5.2981 -0.0005 0.0010 0.0012 4.2390 4.3658 Low frequencies --- 615.2687 623.0837 734.3899
Optimization of Furan (MP2 6-311G(d,p))
The log file can be found [here]. The Gaussian calculation summary is presented in a table below,
| Property | Value |
|---|---|
| File Name | Furan_OPT_MP2_output |
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RMP2-FC |
| Basis Set | 6-311G(d,p) |
| Energy | -229.42804719 a.u. |
| RMS Gradient Norm | 0.00000194 a.u. |
| Dipole Moment | 0.7751 D |
| Point Group | C1 |
| Time Taken | 5 minutes and 6.3 seconds |
The optimization was found to be successful in converging to a value as shown below,
Item Value Threshold Converged?
Maximum Force 0.000003 0.000015 YES
RMS Force 0.000001 0.000010 YES
Maximum Displacement 0.000050 0.000060 YES
RMS Displacement 0.000017 0.000040 YES
Predicted change in Energy=-4.363474D-10
Optimization completed.
-- Stationary point found.
Vibrational Analysis The log file for this calculation can be found [here].
Low frequencies --- -0.8367 -0.7193 -0.6016 -0.0004 0.0008 0.0011 Low frequencies --- 570.2156 622.8546 700.9792