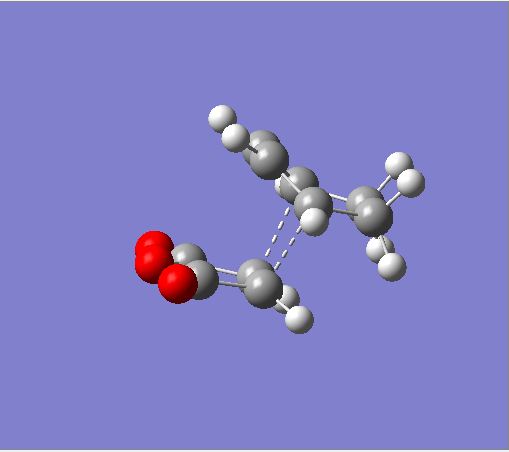
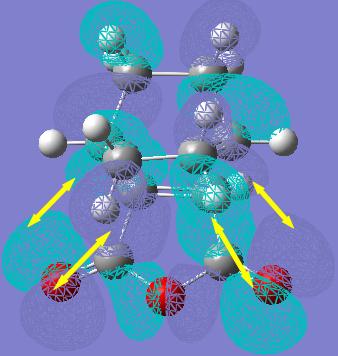
Rep:Mod:hcn06report3
Module 3, Experiment 3: The Transition State
In this experiment, molecular orbital-based methods will be used to solve Schrodinger equations numerically for transition structures in larger molecules and locate transition structures based on the local shape of a potential energy surface so that the geometries of the transition states, the pathway and the barrier heights can be obtained.
The Cope Rearrangement Tutorial
To locate the low-energy minima and transition structures on the C6H10 potential energy surface and to determine the preferred reaction mechanism.
(a)
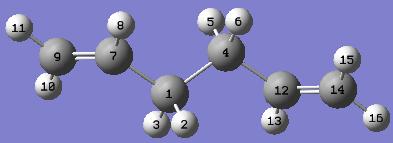
A molecule of 1,5-hexadiene with an "anti" linkage for the central four C atoms is created using GaussView. The structure is cleaned and optimised at a HF/3-21G level of theory.
- Energy of the optimised structure with HF/3-21G: -231.69260235 a.u.
The structure is then symmetrized for the point group determination.
- Point group of the optimised structure: C2
(b)
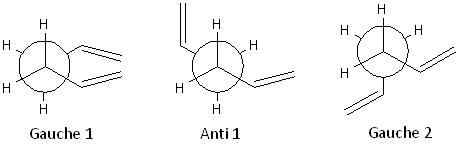
Another molecule of 1,5-hexadiene with a "gauche" linkage for the central four C atoms is created and optimised at the same level of theory as in part a (HF/3-21G). This structure is predicted to have a higher energy than the anti structure that has just been optimised as the largest substituents, which are the C=C double bonds, on both ends of the central C-C bond, are spacially further away from each other and hence produce less steric hindrance in the anti structure than in the gauche structure. As the gauche structure is sterically more hindered, its energy will be higher.
- Energy of the optimised structure with HF/3-21G: -231.69266122 a.u.
However, the computed calculation shows that the gauche conformation has a slightly lower energy (by 0.04 kcal/mol) than the anti conformation. This contradicts with the prediction made and may be due to the interaction between the π electrons of the terminal C=C double bond and its nearby vinyl proton; this is usually called as the CH-π interaction. Besides, the method and the basis set used, which determine the use of approximations made in solving the Schrodinger equation and the accuracy of the calculations, can also affect the energy of the final structure.
- Point group of the optimised structure: C1
This structure has no symmetry at all.
(c) As the gauche conformation is only slightly lower in energy than the anti conformation, all possible conformations of the 1,5-hexadiene will be drawn and optimised in order to determine the lowest energy conformation. This will be used as a reference for the activation energies and enthalpies later.
As there are 3 readily rotating C-C bonds, each with 3 rotational minima, in the molecule of 1,5-hexadiene, the molecule should have 27 conformations. However, only 10 of them are energetically distinct, together with 2 enantiomeric conformations, due to symmetry and enantiometric relationships.
These 3 conformers are formed by rotating the central C-C bond with anti-parallel vinyl groups:
These 3 conformers are formed by rotating the central C-C bond with parallel vinyl groups; the Gauche 3 and Gauche 4 conformers are enantiomers:
These 3 conformers are formed by rotating the central C-C bond while one of the Csp3-Csp2 bonds is s-cis orientated:
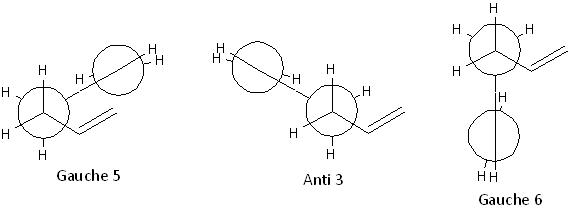
These 3 conformers are formed by rotating the central C-C bond while both of the Csp3-Csp2 bonds are s-cis orientated; the Gauche 7 and Gauche 8 conformers are enantiomers:
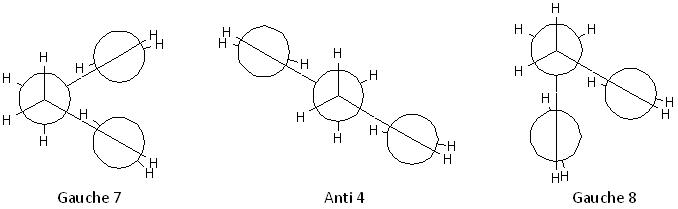
The structures, points groups and energies of each conformation are shown in the table below:
| Conformer | Structure | Point Group | Energy (a.u.)
HF/3-21G |
Energy (kcal/mol) |
|---|---|---|---|---|
| Gauche 1 | 
|
C2 | -231.69166696 | 0.62 |
| Gauche 2 | 
|
C2 | -231.69153035 | 0.71 |
| Gauche 3 | 
|
C1 | -231.69266122 | 0.00 |
| Gauche 4 | 
|
C1 | -231.69266122 | 0.00 |
| Gauche 5 | 
|
C1 | -231.68916016 | 2.20 |
| Gauche 6 | 
|
C1 | -231.68961570 | 1.91 |
| Gauche 7 | 
|
C2 | -231.68771610 | 3.10 |
| Gauche 8 | 
|
C2 | -231.68771610 | 3.10 |
| Anti 1 | 
|
C2 | -231.69260236 | 0.04 |
| Anti 2 | 
|
Ci | -231.69253528 | 0.08 |
| Anti 3 | 
|
C1 | -231.69097053 | 1.06 |
| Anti 4 | 
|
C2h | -231.68907066 | 2.25 |
The conformation Gauche 3 and its enantiomeric conformation Gauche 4 with a C1 point group and an energy of -231.69266122 a.u. are the lowest energy conformations of 1,5-hexadiene predicted by the calculation at the HF/3-21G level of theory. Thus, they will be used as a reference for the calculated activation energies and enthalpies.
All the conformational energies of 1,5-hexadiene are very similar to each other. The energy difference between the lowest energy gauche conformation and the lowest energy anti conformation is only 0.04 kcal/mol.
It is important to note that the HF method includes no electron correlation in the calculation. Therefore, many electronic effects, including the CH-π interaction mentioned, are not considered properly and it treats the 1,5-hexadiene too much like n-butane.
(d) All the structures that have just been optimised can be identified in the table of the [Appendix 1] given, with all the point groups and energies identical. Two enantiomers of two of the gauche conformers are also included in my result.
(e) The anti conformation with a Ci point group has already been included in my result. The energy obtained is identical to that given in the table of the [Appendix 1] given.
(f) As it is noted that the method and basis set used for the calculation can affect the optimisation of the structure, the anti conformation with a Ci point group is reoptimised at the B3LYP/6-31G* level (higher level) of theory and the comparison is shown below.
- Energy of the optimised structure with HF/3-21G: -231.69253528 a.u.
- Energy of the optimised structure with B3LYP/6-31G*: -234.55971534 a.u.
The energy of the optimised structure at a higher level of theory is a lot (1799 kcal/mol) higher than that from the HF/3-21G calculation.
| Calculation | HF/3-21G | B3LYP/6-31G* |
|---|---|---|
| Final structure | 
|
|
| Dihedral angle C(9)=C(7)-C(1) (°) | 124.808 | 125.215 |
| Dihedral angle C(14)=C(12)-C(4) (°) | 124.810 | 125.215 |
| Dihedral angle C(7)-C(1)-C(4) (°) | 111.349 | 112.648 |
| Dihedral angle C(1)-C(4)-C(12) (°) | 111.353 | 112.648 |
| Dihedral angle H(11)-C(9)-H(10) (°) | 116.311 | 116.292 |
| Dihedral angle H(15)-C(14)-H(16) (°) | 116.311 | 116.292 |
| Dihedral angle H(2)-C(1)-H(3) (°) | 107.714 | 106.702 |
| Dihedral angle H(5)-C(4)-H(6) (°) | 107.714 | 106.702 |
| C(9)=C(7) bond distance (Å) | 1.31615 | 1.33825 |
| C(14)=C(12) bond distance (Å) | 1.31614 | 1.33825 |
| C(7)-C(1) bond distance (Å) | 1.50889 | 1.50709 |
| C(1)-C(4) bond distance (Å) | 1.55284 | 1.55508 |
| C(4)-C(12) bond distance (Å) | 1.50890 | 1.50709 |
| H(11)-C(9) bond distance (Å) | 1.07338 | 1.08596 |
| H(10)-C(9) bond distance (Å) | 1.07464 | 1.08782 |
| H(15)-C(14) bond distance (Å) | 1.07464 | 1.08782 |
| H(16)-C(14) bond distance (Å) | 1.07338 | 1.08596 |
| H(2)-C(1) bond distance (Å) | 1.08555 | 1.10031 |
| H(3)-C(1) bond distance (Å) | 1.08476 | 1.09858 |
| H(5)-C(4) bond distance (Å) | 1.08557 | 1.10031 |
| H(6)-C(4) bond distance (Å) | 1.08476 | 1.09858 |
The overall geometry after applying a higher level of theory does not change much. Some of the bond distances stay the same and some just changes by 0.01 to 0.02 Å. Similarly, some of the dihedral angles stay the same and some just changes by 0.04 to 1°.
The bond distances and dihedral angles of the structure optimised at the B3LYP/6-31G* level of calculation are generally slightly longer and wider than those at the lower level. The final structure optimised at the B3LYP/6-31G* level of calculation is also more symmetric.
(g) In order to obtain the final energies with some additional terms for comparisons with the experimentally measured quantities, a frequency calculation has to be carried out. The frequency calculation can also be used to characterise the critical point, confirming that it is a minimum in this case.
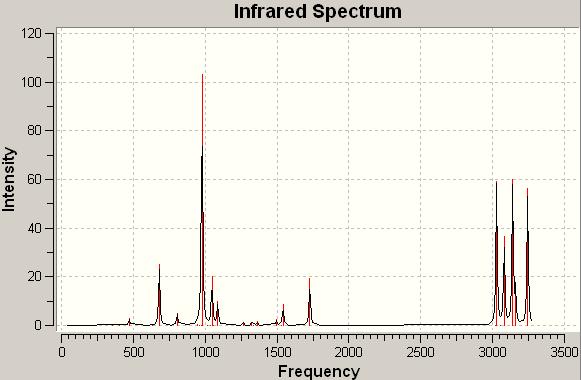
An IR spectrum for the anti conformation with a Ci point group
It is checked that there are no imaginary frequencies, only real ones.
From the result file, a list of energies with additional terms can be obtained:
:Sum of electronic and zero-point Energies = -234.416226 a.u.
- (This shows the potential energy at 0 K including the zero-point vibrational energy.)
:Sum of electronic and thermal Energies = -234.408944 a.u.
- (This shows the energy at 298.15K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature.)
:Sum of electronic and thermal Enthalpies = -234.407999 a.u.
- (This shows the energy containing an additional correction for RT (H = E + RT), which is particularly important when looking at dissociation reactions.)
:Sum of electronic and thermal Free Energies = -234.447806 a.u.
- (This shows the energy including the entropic contribution to the free energy (G = H - TS).)
These corrections can also be calculated at other temperatures.
Literature
- Brandon G. Rocque, Hason M. Gonzales and Henry F. Schaefer III , Molecular Physics, 2002, Vol. 100, No. 4, 441-446 DOI:2 10.1080/0026897011008141 2
Optimizing the "Chair" and "Boat" Transition Structures
A transition structure optimisation will be set up by 3 methods:
- computing the force constants at the beginning of the calculation
- using the redundant coordinate editor
- using QST2
(a) An allyl fragment (CH2CHCH2) is created and optimised using the HF/3-21G level of theory.
The optimized allyl structure is then used to create a chair transition state with the distance between the terminal ends of the allyl fragments to be approximately 2.2 Å apart.
(b) A transition state can be optimised manually in two different ways. If there is a reasonable guess for the transition structure geometry, the easiest way to produce the negative direction of curvature (i.e. the reaction coordinate) is to compute the force constant matrix (also known as the Hessian) in the first step of the optimization which will then be updated as the optimization proceeds.
This will be demonstrated by optimising the chair transition state using the Hartree Fock method and the default basis set 3-21G.
The optimised structure is checked to be the same as the one shown in the [Appendix 2] given.
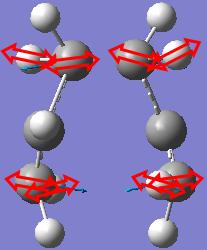
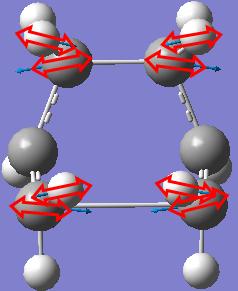
The frequency calculation gives an imaginary frequency of magnitude 817.954 cm-1 and the motion of that animated vibration is shown below.
The vibration is checked to be the one corresponding to the Cope rearrangement.
(c) However, if the guess structure for the transition structure is far from the exact structure, computing the force constant matrix in the first step of the optimisation may not produce the reaction coordinate as the curvature of the surface may be significantly different at points far removed from the transition structure. A better transition structure can be generated by freezing the reaction coordinate and minimizing the rest of the molecule. Once the molecule is fully relaxed, the reaction coordinate can then be unfrozen and the transition state optimization is started again. One advantage of doing this, is that it may not be necessary to compute the whole force constant matrix once this has been done, and just differentiating along the reaction coordinate might give a good enough guess for the initial force constant matrix. This can save a considerable amount of time in cases where the force constant calculation is expensive.
This will be demonstrated by optimising the same guess chair transition state using the Hartree Fock method and the default basis set 3-21G.
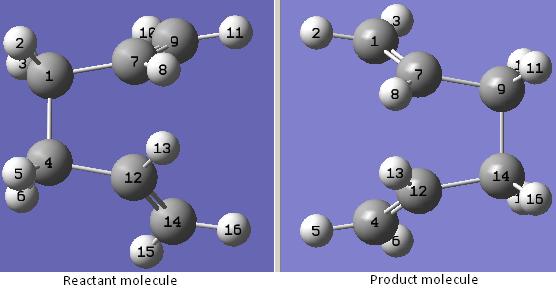
The transition state is first optimised with two of the terminal carbons from the allyl fragments, which form/break a bond during the rearrangement, frozen, as if it were a minimum.
The optimised structure is a lot like the transition optimised in section (b), except the bond forming/breaking distances are fixed to 2.2 Å.
(d) The bonds that were previously frozen are made unfrozen and optimised by using a normal guess Hessian modified to include the information about the two coordinates that are differentiating along.
A table to show the comparisons between the structure optimised by computing the force constants at the beginning of the calculation and that optimised by using the redundant coordinate editor
| Structure optimised by computing the force constants at the beginning of the calculation | Structure optimised by using the redundant coordinate editor | |
|---|---|---|
| Structure |
|
|
| Bond forming/bond breaking bond lengths (Å) | 2.02014, 2.02034 | 1.55081, 4.39027 |
The structures of the transition states optimised by the two different methods are quite different. The structure optimised by using the redundant coordinate editor is very similar to the Gauche 1 conformation of the 1,5-hexadiene with a point group of C2 while that optimised by computing the force constants at the beginning of the calculation is more symmetrical and looks more like the guess transition state before the optimisation.
The bond forming/bond breaking bond lengths of the structure optimised by using the redundant coordinate editor are very different (one is about 3 times longer than the other) while those of the structure optimised by using the redundant coordinate editor are similar to each other.
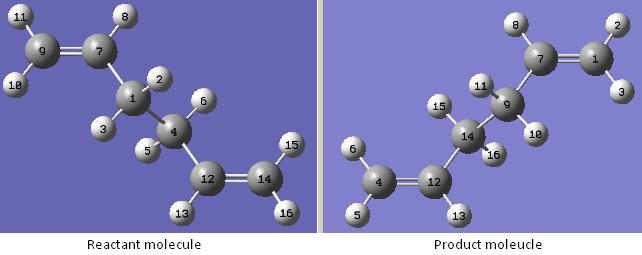
(e) Optimisation of a transition state using the QST2 method allows one to specify the reactants and products for a reaction and the calculation will interpolate between the two structures to try to find the transition state between them. One advantage of this method is that it is fully automated. This will be demonstrated by optimising a boat transition structure.
The optimised Anti 2 conformation of 1,5-hexadiene with a point group of Ci is used as the optimised reactant molecule.
First, the numbering for the product molecule is changed manually so that it corresponds to the numbering of the reactant molecule.
The structures are then optimised to a transition state using the QST2 method.
However, the optimised transition state shows that the job fails.
It looks a bit like the chair transition structure but more dissociated. The QST2 method fails to locate the boat transition structure from the reactant and product structures used because when the calculation linearly interpolated between the two structures, it simply translated the top allyl fragment and did not even consider the possibility of a rotation around the central bonds.
Therefore, the reactant and product geometries have to be modified so that they are closer to the boat transition structure.
The QST2 calculation is then run again using these molecules.
This time, the boat transition structure obtained converges.
It is checked that there is only one imaginary frequency of magnitude 840.118 cm-1 and the motion of that animated vibration is shown below.
The vibration is checked to be the one corresponding to the Cope rearrangement.
There is another more reliable method, called the QST3 method, that allows one to input the geometry of a guess transition structure. However, due to the time limit, this method will not be demonstrated.
(f) As noted previously, the chair transition state obtained is connected to the Gauche 1 conformation of the 1,5-hexadiene with a point group of C2 while the boat transition state obtained is connected to the Anti 2 conformation of 1,5-hexadiene with a point group of Ci. However, it is almost impossible to predict which conformer the reaction paths from the transitions structures will lead to.
The Intrinisic Reaction Coordinate (IRC) method allows one to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. This creates a series of points by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest. This will be demonstrated with the chair transition structure previously optimised by computing the force constants at the beginning of the calculation. As the reaction coordinate is symmetrical, only the forward direction will be computed. The force constants are chose to be calculated only once. The number of points along the IRC is chosen to be 50.
When the IRC calculation has finished, all the intermediate geometries are obtained and the progress of the calculation is checked. It can be seen that the minimum geometry has not been reached yet.
There are 3 options to improve the calculation:
- Take the last point on the IRC and run a normal minimization.
- (This approach is the fastest, but if the guess transition structure is not close enough to a local minimum, it may end up in the wrong minimum.)
- Restart the IRC and specify a larger number of points until it reaches a minimum.
- (This approach is more reliable but if too many points are needed, the calculation can also veer off in the wrong direction after a while and end up at the wrong structure.)
- Redo the IRC specifying that you want to compute the force constants at every step.
- (This approach is the most reliable but also the most expensive and is not always feasible for large systems.)
The same optimised chair transition structure is used for the three approaches described above and the results are compared below.
| Approach 1 | Approach 2 with 100 points | Approach 2 with 200 points | Approach 3 |
|---|---|---|---|
|
|
|
|
The similarity among all the transition states produced is that they are all aromatic.
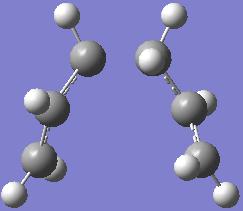
Approach 1:
- The structure of the product looks like the transition structure optimised by using the redundant coordinate editor. This shows that the guess transition structure is not close enough to a local minimum and hence the calculation ends up in the wrong minimum.
Approach 2:
- The number of points along the IRC is first increased to 100.
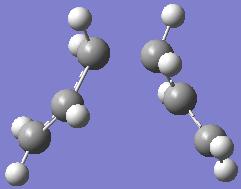
- However, it can be seen that the minimum still has not been reached. The number of points along the IRC is then increased to 200. Again, the file is deposited onto the SCAN chemistry database and the calculation takes 8 hours (longer than the time needed for Approach 3).
- The structure produced with 200 points along the IRC is again back to something like the transition state. This is because the number of points along the IRC is set too large that the calculation veers off in the wrong direction after a while and ends up at the wrong structure.
- If a better guess of the number of points along the IRC can be made, Approach 2 should be a good choice for the calculation.
Approach 3:
- Although this approach takes longer than Approach 1, it gives the product molecule straight away and is most reliable.
(g) In order to obtain the activation energies for the reaction via both transition structures, the chair and boat transition structures will have to be reoptimised using the B3LYP/6-31G* level of theory and the frequency calculations have to be carried out.
| Gauche 1 conformation of reactant optimised at a HF/3-21G level of theory | Chair transition state optimised at a B3LYP/6-31G* level of theory | Anti 2 conformation of reactant optimised at a HF/3-21G level of theory | Boat transition state optimised at a B3LYP/6-31G* level of theory | |
|---|---|---|---|---|
| Geometry |
|
|
|
|
| Energy (a.u.) | -231.69153035 | -234.55868303 | -231.69253528 | -234.55933662 |
The difference in energy between the Gauche 1 conformation of reactant and the Chair transition state at the two levels of theory is 1799 kcal/mol while that between the Anti 2 conformation of reactant and the Boat transition state at the two levels of theory is also 1799 kcal/mol.
The geometries of the reactants and the transition states at the two levels of theory are reasonably similar, but the energy differences are markedly different. Therefore, it is often more computational efficient to map the potential energy surface using the low level of theory first and then to reoptimize at the higher level.
The energies with the zero-point correction at 0K and the energies with thermal correction at 298.15 K can be found under the Thermochemistry data in the output file. The table below shows a summary of the energies at the two levels of theory.
| HF/3-21G | HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | B3LYP/6-31G* | |
|---|---|---|---|---|---|---|
| Electronic energy (a.u.) | Sum of electronic and zero-point energies (a.u.) | Sum of electronic and thermal energies (a.u.) | Electronic energy (a.u.) | Sum of electronic and zero-point energies (a.u.) | Sum of electronic and thermal energies (a.u.) | |
| at 0K | at 298.15K | at 0K | at 298.15K | |||
| Chair transition state | -231.56057709 | -231.411778 | -231.406545 | -234.55868303 | -234.415315 | -234.408060 |
| Boat transition state | -231.60729995 | -231.451881 | -231.446458 | -234.55933662 | -234.415745 | -234.408572 |
| Anti 2 conformation of reactant | -231.69253528 | -231.528987 | -231.522061 | -234.55971534 | -234.416226 | -234.408944 |
The activation energies via the chair and the boat transition structures at 0 K and 298.15K can be deduced from the table above.
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Experimental value | |
|---|---|---|---|---|---|
| at 0K | at 298.15K | at 0K | at 298.15K | at 0K | |
| ∆E(Chair) (kcal/mol) | 73.55 | 72.49 | 0.57 | 0.55 | 33.5 ± 0.5 |
| ∆E(Boat) (kcal/mol) | 48.38 | 47.44 | 0.30 | 0.23 | 44.7 ± 2.0 |
The activation energies via both of the transition states obtained at the HF/3-21G level of theory are much nearer to the experimental values and are much larger than those obtained at the B3LYP/6-31G* level of theory.
Literature
- Shogo Sakai, International Journal of Quantum Chemistry, 2000, Vol. 80, 1099–1106 DOI:<1099::AID-QUA59>3.0.CO;2-C 10.1002/1097-461X(2000)80:4/5<1099::AID-QUA59>3.0.CO;2-C
Mini Project: The Diels Alder Cycloaddition
The Diels Alder reaction belongs to a class of reactions known as pericyclic reactions, in which bonds are made or broken in a concerted (i.e. with no intermediates during the course of the reaction) cyclic transition state.
The π orbitals of the dieneophile are used to form new σ bonds with the π orbitals of the diene. Whether or not the reactions occur in a concerted stereospecific fashion (allowed) or not (forbidden) depends on the number of π electrons involved. In general the HOMO/LUMO of one fragment interacts with the HOMO/LUMO of the other reactant to form two new bonding and anti-bonding MOs. The nodal properties allow one to make predictions according to the following rule:
- If the HOMO of one reactant can interact with the LUMO of the other reactant then the reaction is allowed.
- The HOMO-LUMO can only interact when there is a significant overlap density. If the orbitals have different symmetry properties then no overlap density is possible and the reaction is forbidden.
If the dieneophile is substituted, with substituents that have π orbitals that can interact with the new double bond that is being formed in the product, then this interaction can stabilise the regiochemistry of the reaction.
The nature of the transition structures of two Diels Alder reactions, one prototypical reaction and one where both diene and dieneophile carry substituents, and where secondary orbital effects are possible, will be stuided using the methods demonstrated previously with GaussView.
The principal orbital interactions involve the π/ π* orbitals of ethylene and the HOMO/LUMO of butadiene. It is referred to as [4s + 2s] since one has 4 π orbitals in the π system of butadiene. The orbitals of ethylene and butadiene and ethylene can be classified as symmetric s or anti-symmetric a with respect to the plane of symmetry shown.
The HOMO of ethylene and the LUMO of butadiene are both s (symmetric with respect to the reflection plane) and the LUMO of ethylene and the HOMO of butadiene are both a. Thus it is the HOMO-LUMO pairs of orbital that interact, and energetically, the HOMO of the resulting adduct with two new σ bonds is a. These will be confirmed in the following quantitative study.
The Reactant Molecule: Cis-butadiene
A cis-butadiene molecule is created and optimised at a HF/3-21G level of theory as it was shown in the previous part that the results obtained are similar at the HF/3-21G and the B3LYP/6-31G* levels of theory.
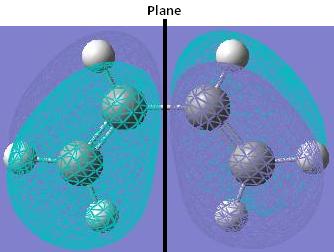
The HOMO of cis-butadiene is asymmetric (a) with respect to the plane of symmetry.
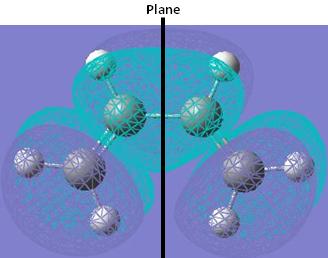
The LUMO of cis-butadiene is symmetric (s) with respect to the plane of symmetry.
These confirms the qualitative explanation at the beginning.
The Ethylene-Cis-butadiene Transition state
As it is given that the transition structure has an envelope type structure, which maximises the overlap between the ethylene π orbitals and the π system of butadiene, a transition structure is created by building a bicycle[2,2,2]octane first and removing the –CH2CH2- fragment and then the bonds between the butane and the ethane fragments. The interfragment distances are set to 2.210Å as it is found in the literature that the interfragment distances of the optimised transition states at a HF/3-21G level of theory are 2.210Å.
As there is a reasonable guess for the transition structure geometry, the reaction coordinate will be obtaiend by computing the force constant matrix in the first step of the optimization which will then be updated as the optimization proceeds.
A table to show the geometric parameters of the ethylene-cis-butadiene transition state
| Bond | Bond length (Å) | Bond | Bond angle (°) |
|---|---|---|---|
| C(9)=C(11) | 1.22388 | C(11)=C(9)....C(3) | 111.407 |
| C(3)....C(9) | 2.19986 | C(9)=C(11)....C(2) | 111.409 |
| C(2)....C(11) | 2.19993 | C(2)=C(1)-C(4) | 121.615 |
| C(3)=C(4) | 1.36753 | C(3)=C(4)-C(1) | 121.616 |
| C(2)=C(1) | 1.36754 | C(9)....C(3)=C(4) | 100.668 |
| C(4)-C(1) | 1.39606 | C(11)....C(2)=C(1) | 100.664 |
In order to obtain the typical sp2 and sp3 C-C bond lengths, a moleucle of but-1-ene is optimised and its C-C bond lengths are shown on the table below.
| Bond | Bond length (Å) |
|---|---|
| sp2C=sp2C | 1.31605 |
| sp2C-sp3C | 1.50951 |
| sp3C-sp3C | 1.54644 |
The van der Waals radius of the C atom is 170 pm.
The C-C bondlength of the partly formed σ C-C bonds in the transition state is much longer than the typical σ C-C bonds and the other C-C bonds in the transition state. This shows that the optimised structure is an “early” transition state. The C-C and C=C bond lengths in the transition state are quite different to the typical bond lengths. This shows that all the C-C bonds in the transitin state can be considered as partial double bonds.
There is only one negative frequency of magnitude 839.434 cm-1 for the transition state. The motion of this vibration corresponds to the reaction path at the transition state and is shown below:
It can be seen from the motion that the formation of the two bonds is synchronous.
The lowest positive frequency has a magnitude of 269.039 and the motion of this vibration is shown below:
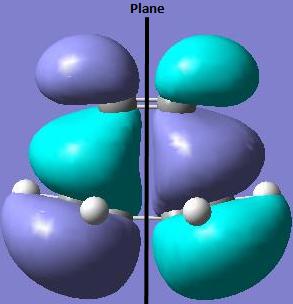
The HOMO of the ethylene-cis-butadiene transition state is asymmetric (a) with respect to the plane of symmetry.
This is due to the orbital interaction between the LUMO of the ethylene (a) and the HOMO of the cic-butadiene (a).
The LUMO of the ethylene-cis-butadiene transition state is symmetric (s) with respect to the plane of symmetry.
Literature
- Joey W. Storer, Laura Raimondi and K. N. Houk, J. Am. Chem. Soc., 1994, 116 (21), 9675-9683 DOI:10.1021/ja00100a037
- Yi Li, and K. N. Houk, J. Am. Chem. Soc., 1993, 115 (16), 7478-7485 DOI:10.1021/ja00069a055
- Shogo Sakai, J. Phys. Chem. A, 2000, 104 (5), 922-927 DOI:10.1021/jp9926894
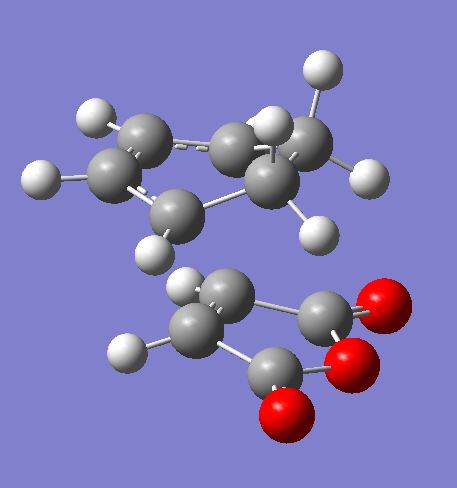
The Cyclohexa-1,3-diene Reaction with Maleic Anhydride
Cyclohexa-1,3-diene undergoes facile Diels-Alder reaction with maleic anhydride to give primarily the endo adduct. The reaction is kinetically controlled so that the exo transition state is higher in energy. The regioselectivity of this reaction will be studied.
The structure of the exo and endo adducts are given but the interfragment distances are not. The interfragment distances are left as they are when the guess transition states are created. As the guess structure of the two transition states may be far from the exact structure, computing the force constant matrix in the first step of the optimisation may not produce the reaction coordinate as the curvature of the surface may be significantly different at points far removed from the transition structure. Therefore, they are first generated by freezing the reaction coordinate and minimizing the rest of the molecule. The reaction coordinate is then unfrozen when the molecule is fully relaxed and the transition state optimization is started again.
The optimised exo transition state
A table to show the bond lengths of the optimised exo transition state
| Bond | Bond length (Å) |
|---|---|
| C(2)….C(19) | 1.54276 |
| C(3)….C(17) | 1.54083 |
| C(4)-C(1) | 1.56334 |
| C(1)=C(2) | 1.54101 |
| C(4)=C(3) | 1.54110 |
| C(3)-C(12) | 1.53969 |
| C(2)-C(9) | 1.54069 |
| C(9)-C(12) | 1.56000 |
| C(17)=C(19) | 1.53628 |
| C(17)-C(23) | 1.51715 |
| C(19)-C(21) | 1.51572 |
| C(23)-O(25) | 1.38336 |
| C(21)-O(25) | 1.38440 |
| C(23)=O(24) | 1.18958 |
| C(21)=O(22) | 1.18931 |
The optimised endo transition state
A table to show the bond lengths of the optimised endo transition state
| Bond | Bond length (Å) |
|---|---|
| C(2)….C(19) | 1.54274 |
| C(3)….C(17) | 1.54081 |
| C(4)-C(1) | 1.55999 |
| C(1)=C(2) | 1.54070 |
| C(4)=C(3) | 1.53970 |
| C(3)-C(12) | 1.54111 |
| C(2)-C(9) | 1.54102 |
| C(9)-C(12) | 1.56000 |
| C(17)=C(19) | 1.53629 |
| C(17)-C(23) | 1.51714 |
| C(19)-C(21) | 1.51573 |
| C(23)-O(25) | 1.38337 |
| C(21)-O(25) | 1.38440 |
| C(23)=O(24) | 1.18958 |
| C(21)=O(22) | 1.18931 |
For both of the transition states, all the C-C bond lengths, including the partly formed σ C-C bonds, are similar to each other. This shows that the transition states have reached or are near the exact structure and all the C-C bonds are delocalised in the transition states.
A table to show the energies of the two transition states
| Transition state | Energy (a.u.) |
|---|---|
| Exo | -606.90823901 |
| Endo | -606.90823907 |
The energies of the two transition states are very similar with the endo adduct being slightly more stable.
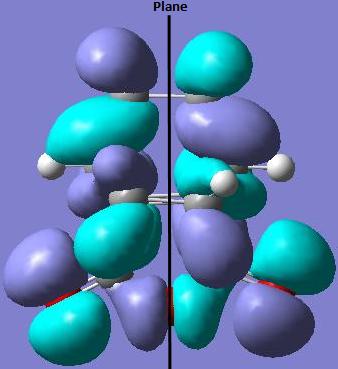
The HOMO of the exo transition state is asymmetric (a) with respect to the plane of symmetry.
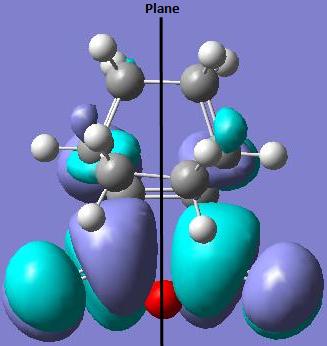
The LUMO of the exo transition state is also asymmetric (a) with respect to the plane of symmetry.
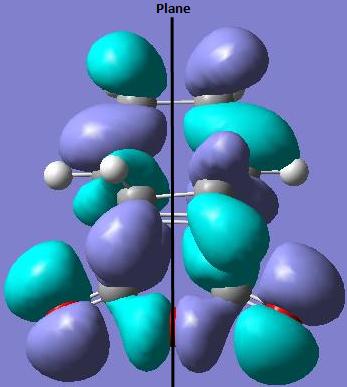
The HOMO of the endo transition state is asymmetric (a) with respect to the plane of symmetry.
The LUMO of the endo transition state is also asymmetric (s) with respect to the plane of symmetry.
Having looked at the HOMOs of the two transition states, it can be seen that the endo transition state is thermodynamically more stable due to the second orbital interactions due to the bonding interactions between the carbonyl groups and the developing π bond at the back of the cis-butadiene.
However, there is no secondary orbital interactions in the HOMO of the exo transition state. The carbonyl groups cannot interact with the developing π bond due to their orientations.