Rep:Mod:hc2213

Introduction

The aim of this Year 3 Computational Laboratory was to determine and analyse the reagents, transition states and products of the Cope rearrangement and the Diels-Alder rearrangement using GaussView 5.0.9. Structures were modeled and optimised using a variety of methods to compute properties; energies, point groups, bond lengths, bond angles, vibrational frequencies and activation energies. Being able to model transition states is an important experimentally as transition states structure have an energy maxima on the reaction coordinate, and are not observable. Computationally only an hypothetical transition state structure can be determined to determine hypothetical physical properties.

Optimisation and frequency calculations can be carried out at many levels of theory:

• HF/3-21G: A Hartree-Fock method is an approximate method of optimisation for the minimal basis set.
• B3LYP/6-31G*: A Density Functional Theory (DFT) optimisation, this is more accurate than the HF method. This DFT method uses the split-valence basis set which includes the s, p and d orbitals because bond formation results in a polarisation of orbitals hence it is important to include basis functions with a higher quantum number.
• AM1 Semi-Empirical: This is the most approximate optimisation method, it is used to determine the molecular orbitals of a molecule to determine the HOMO and LUMO computationally. A semi-empirical method does not require input of a specific basis set as molecule mechanisms are defined via a force field of fitted parameters rather than by quantum.

HF/3-21G	B3LYP/6-31G*	AM1 Semi-Empirical

Optimisation to a minimum determines the lowest energy structure for a particular molecule. This is not an appropriate method for determine transition structures as they are an energy maxima. Transition states can be optimised to TS (Berny) TS QST2 or TS QST3. The TS Berny method involves "guessing" the transition structure using chemical intuition to then optimise it then determining if the transition state has been found by computing the Intrinsic Reaction Coordinate (IRC). The TS QST2 method requires building the reactant and product molecule in the same molecule group and labelling the atoms such that they correspond to the rearrangement of atoms during reaction then optimising to obtain a transition state structure. The TS QST3 method is the most reliable but was not used during this investigation.

Nf710 (talk) 16:48, 3 December 2015 (UTC) Nice intro. could have gone into more detail with the particularly HF. but good general understanding

The Cope Rearrangement

The Cope rearrangement is a thermal [3,3]-sigmatropic reaction belonging to a class called pericyclic reactions. There has previously been much controversy over the mechanism by which the Cope rearrangement occurs, extensive computational and experimental research into the mechanism was carried out. It is now widely accepted that the 1,5-hexadiene undergoes a concerted reaction via a chair or boat transition structure.

The Cope Rearrangement Mechanism

Optimising the Reactants and Products - Conformations of 1,5 Hexadiene

Due to free rotation about the central C_sp3-C_sp3 bond the 1,5-hexadiene is able to adopt various conformations as the dihedral angle varies. Some of these conformations will be analysed in the sections below.

The reactant and product are both a 1,5 dihexadiene structure which was modeled using GaussView 5.0.9. To produce a reactant molecule with an anti-periplanar geometry the dihedral angle was set to 180°; to produce a reaction molecule with a gauche geometry the dihedral angle was set to 60°. The drawn strcture can be cleaned using the clean tool under the edit menu.

Optimisation of 1,5-hexadiene was carried out at the HF/3-21G level to obtain the energies for each conformation as shown in the table below. The molecule was symmetrized to obtain the point group, this however changes properties such as energy.

Table showing the energies and point groups of conformations of 1,5-hexadiene.

Conformation	GaussView HF/3-21G Optimised Structure	Point Group	Energy /Hartree	Energy /Kcalmol-1
Anti1	1,5-Hexadiene "Anti1" Conformation	C2	-231.69260236	0.04
Gauche2	1,5-Hexadiene "Gauche2" Conformation	Ci	-231.69166697	0.62
Anti2	1,5-Hexadiene "Anti2" Conformation	Ci	-231.69253528	0.08

The Anti1 has the lowest total energy by 9.3539x10-4 a.u hence I would have expected an anti-periplanar conformer to be the lowest energy. According to Appendix 1 the Gauche3 conformer is the lowest energy conformer with an energy of -231.69266 Hartrees, this is despite the Anti conformation having less steric hindrance. The reason for the stabilisation of the Gauche conformer is due to a secondary orbital interaction between the two π systems, the LUMO of one is able to interact favorably with the HOMO of another to result in a stabilisation factor.

Nf710 (talk) 16:51, 3 December 2015 (UTC) Good attempt but not quite. it is two bonding interactions interacting inphase because of the twist therefore allowing them to have favourable intactions. you could have shown this in the orbital of the .chk file.

1,5-Hexadiene Anti2 Conformation - B3LYP/6-31G* Optimisation

A frequency and optimisation of the Anti2 conformation of 1,5-Hexadiene at a B3LYP/6-31G* level was them carried out. The geometries of the optimised reactant molecule for both the HF/3-21G and B3LYP/6-31G* levels. The B3LYP/6-31G* calculation relies upon fewer approximations, hence the geometries of the Anti2 conformation determined under this calculation are more accurate than those computed under the HF/3-21G optimisation. The difference in the bond lengths and bond angles is not substantial.

Comparison of the Geometries of Different Optimisation Methods

	Atoms	HF/3-21G	B3LYP/6-31G*	Labelled GaussView Structure
Bond	C1-C2 = C5-C6	1.31613	1.33350
	C2-C3 = C4-C5	1.50891	1.50419
	C3-C4	1.55275	1.54816
Angle	C1-C2-C3 = C4-C5-C6	124.806	125.300
	C2-C3-C4 = C3-C4-C5	111.349	112.671

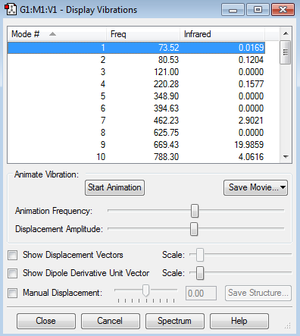
The frequency component of the calculation at the B3LYP/6-31G* level produces vibrational frequencies of the Anti2 conformation; all of the frequencies are real (positive). Thermochemistry data, available in the log file, was also determined by this calculation, this can be used to provide vital information about the energetics of the reaction; the driving force and activation barrier.

Vibrational Frequencies	Thermochemistry Data

An infra-red (IR) spectrum was plotted using the tool on GaussView. The characteristic shifts for 1,5-hexadiene are; =C-H stretch (3150 cm^-1) and =C-H bending (950 cm^-1) to indicate an alkene and C-H stretch (3025 cm^-1) and C-H bend (1480 cm^-1) to indicate the alkane linker.

Infrared Spectrum of the Anti2 Conformation at the B3LYP/6-31G* Level

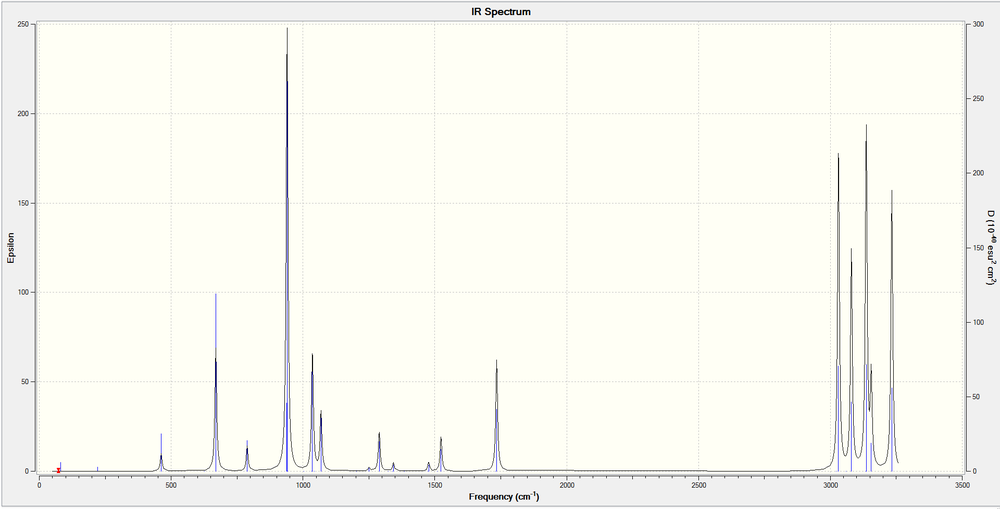
Nf710 (talk) 16:56, 3 December 2015 (UTC) All your energies are good and nice comparison of geoms

Optimising Transition Structure

There are two potential transition structures via which this reaction can proceed; the chair and the boat. To model each of these structures, an allyl fragment (CH₂CHCH₂) was drawn and optimised to a HF/3-21G level of theory. To model each transition structure, two allyl fragments need to be combined.

The "Chair" Transition Structure Optimisation

The chair transition state was optimised by two different methods to draw comparisons between them.

The guessing method involved aligning the two allyl fragments such that the terminal ends are 2.2 Å apart to resemble a chair transition state structure. The guess structure of the transition state undergoes an optimisation and frequency calculation under a TS (Berny) in order to determine a force constant. To set-up this calculation, the force constant was to be calculated once with the keywords "Opt=NoEigen" this is to prevent the calculation failing due to two imaginary (negative) frequencies being located. An imaginary frequency of -817.92 was obtained, this confirms there is only one transition structure with a corresponding Hessian matrix. As there is only one negative frequency, this confirms there is only one transition structure present, hence the reaction mechanism of the Cope Rearrangement is concerted. Transition state structures have a negative frequency due to having a negative force constant.

$f=\frac{1}{2\pi }\sqrt{\frac{k}{m}}$

As can be interpreted from the equation above, to compute frequency from the force constant requires taking the square root of the force constant, which is negative, hence an imaginary frequency is obtained.

The force constant is a measure of the curvature of the potential energy close to the equilibrium extension of the bond, using the gradient of the optimised transition structure and determining an differential can then be applied to quantum theory using the Schrödinger equation to compute the quantised energies for the transition structure.

Nf710 (talk) 16:59, 3 December 2015 (UTC) Well done very clear explanation

Job Type to compute a Transition State and Force Constants	Vibrating Chair Transition Structure

The next method by which the transition state structure was optimised was using the Freeze Coordinate method. To set up the freeze coordination, the bonds between the terminal ends of each allyl fragment were frozen, this was then optimised at a HF/3-21G level. Bond freezing is a method used on GaussView to eliminate some degrees of freedom, hence the molecule becomes somewhat fixed in the chair position when optimised. The chk file generated from the optimisation of the frozen coordinate molecules was then set up for the bond derivative of the frozen bonds, followed by optimisation for a TS (Berny) at the HF/3-21G basis set. A single imaginary frequency was computed by the GaussView calculation, this is again due to a negative force constant as mentioned above.

Computing the transition structures using two different methods does not result in a significant difference in the geometry of the transition structure; hence either method can be used reliably.

Comparison of the Geometries of Different Transition Structures

	Atoms	Guess Structure	Freeze Coordinate Structure	Labelled GaussView Structure of Chair TS
Bond	C1-C2 = C5-C6	1.38925	1.38931
	C2-C3 = C4-C5	1.38929	1.38928
	C3-C4	2.02039	2.02061
Angle	C1-C2-C3 = C4-C5-C6	120.503	120.527
	C2-C3-C4 = C3-C4-C5	101.854	101.851

Nf710 (talk) 17:02, 3 December 2015 (UTC) excellent comparison of geoms, you have gone beyond the script here.

The "Boat" Transition Structure Optimisation

The boat transition structure was optimised using the QST2 method by specifying the reagent and the product with the C_i point group. The atoms of the reactant and product need to be numbered such that it is obvious that a rearrangement has occurred, inconsistent numbering would result in a failed calculation. Running a TS(QST2) optimisation and frequency calculation for the reactant and product structures initially resulted in a failed calculation. This is due to the geometry of the molecule, the dihedral angle (C4-C6-C9-C12 on the reactant and C2-C1-C14-C12 on the product) needed to be alter to 0° then the inside angle (on reactant; C4-C6-C9 and C6-C9-C12, on product; C2-C1-C14 and C1-C14-C12) needed to be altered to 100°. Running a optimisation and frequency calculation using the QST2 method gives a structure with only one imaginary frequency at -839.83.

Reagent and Product for the Cope rearrangement Set up for QST2

All your frequencies correct. excellently detailed comparison

Intrinsic Reaction Coordinate (IRC)

Upon observation of the chair and boat transition structures it is not possible to predict which conformer leads to which path, for this a method known as the Intrinsic Reaction Coordinate (IRC) needs to be used. IRC is a method which allows you to follow the lowest energy path along 3N-6 paths, by assuming no kinetic energy, from a transition structure to its local minimum. It is a sequence of constrained geometry optimisations.

The IRC calculation for the freeze bond optimised chair transition state structure gave rise to 44 geometries. The calculation was run to find 50 points, as only 44 were found, this indicates the lowest energy geometry has been obtained at the final (44th) geometry as this is the minima as can be seen on the IRC plot and by looking at the log file as this shows that the energy has converged. To confirm this is in fact the transition structure, an optimisation of the final structure to a minimum was computed, in order to compare the energy and gradient.

Plot of the IRC Path	Final (44th) Geometry			Re-Optimised Geometry
	GaussView Structure	Energy	Gradient	GaussView Structure	Energy	Gradient
		-231.69157891	0.00015225		-231.69166702	0.00000475

As is evident from the structure above that re-optimisation at the HF/3-21G level does not greatly impact upon the structure, hence the minimum structure obtained by IRC is a reliable representation of the lowest energy conformer. Upon comaprison of this structure with those in Appendix 1 , the lowest energy conformer is the "Gauche3" conformation. The energy of the re-optimised Gauche3 structure gives an energy close to that provided in Appendix 1, the slight difference can be accounted for as computational error and potentially eliminated by optimisation at a DFT level of theory.

Nf710 (talk) 17:06, 3 December 2015 (UTC) Well doen for identifying the correct conf.

Activation Energies

Calculating the activation energies of the chair and boat transition states was then calculated using computations to determine energies.

The HF/3-21G optimised structures were then reoptimised at a DFT B3LYP/6-31G* level of theory, using an already optimised structure reduces the computational time and strength required. Upon investigation of the log files for each optimised structure, you can determine that the energies have converged, this allows comparison of the energies between the reactants and transition structures.

The geometries of the reactant and transitions state structures at Hartree-Fock optimisation and DFT optimisation have been compared and tabulated. Optimisation using DFT gives slightly altered bond lengths and angles, this is due to the consideration of a larger basis set. The difference in geometry is not considered significant as the differences are only between 0.1-0.01 Å.

Comparison of the Bond Lengths of the Transition Structures Optimised to a B3LYP/6-31G* Level.

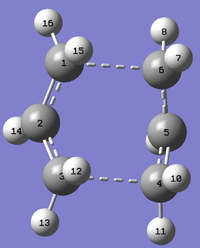
Bond	Anti2 HF/3-21G	Anti2 B3LYP/6-31G*	Chair HF/3-21G	Chair B3LYP/6-31G*	Boat HF/3-21G	Boat B3LYP/6-31G*
C1-C2 = C5-C6	1.31613	1.33350	1.38925	1.40762	1.38141	1.39325
C2-C3 = C4-C5	1.50891	1.50419	1.38929	1.40760	1.38138	1.39326
C3-C4	1.55275	1.54816	2.02039	1.96676	2.14055	2.20679
C6-C1			2.02040	1.96690	2.14034	2.20683

Comparison of the Angles of the Transition Structures Optimised to a B3LYP/6-31G* Level.

Angle	Anti2 HF/3-21G	Anti2 B3LYP/6-31G*	Chair HF/3-21G	Chair B3LYP/6-31G*	Boat HF/3-21G	Boat B3LYP/6-31G*
C1-C2-C3 = C4-C5-C6	124.806	125.300	120.503	119.927	121.701	122.241
C2-C3-C4 = C3-C4-C5	111.349	112.671	101.854	103.663	103.386	103.475

Upon comparison of energies, the difference between the HF/3-21G method and the B3LYP/6-31G* method is significant, particularly when the difference is converted from Hartree to kcalmol^-1 and kJmol^-1;1 Hartree = 627.509 kcal/mol^-1. Activation energy is the minimum energy required for a reaction to proceed via a transition state; a measure of the activation barrier. The activation energies were calculated using the thermochemsitry data; the energy of the reactant was subtracted from the energy of the transition state (chair or boat) and then multiplied by 627.509 kcalmol^-1 to convert the units from Hartrees to kcalmol^-1, other values are not converted into kcalmol^-1 because the value obtained would be very large. The activation energies conclude that the chair transition structure is the more likely than the boat because it is formed via the lowest energy route, particularly when thermal energy is applied.

Summary of Energies /Hartree

Structure	Energy		Electronic and ZPE (0 K)		Electronic and Thermal Energy (298.15 K)
	HF/3-21G	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G*
Anti2	-231.69253528	-234.61171063	-231.539539	-234.469216	-231.532565	-234.461869
Chair TS	-231.61932246	-234.55693103	-231.466700	-234.414909	-231.461341	-234.408981
Boat TS	-231.60280212	-234.54307872	-231.450930	-231.450930	-231.445299	-234.396014

Activation Energies /kcalmol^-1

Structure	HF/3-21G at 0 K	HF/3-21G at 298.15 K	B3LYP/6-21G* at 0 K	B3LYP/6-21G* at 298.15 K	Experimental 0 K
Chair	45.707	44.694	34.375	33.188	33.5 ± 0.5
Boat	55.603	54.760	48.067	41.325	44.7 ± 2.0

It can be concluded that geometries do not need optimisation at a higher basis set to produce accurate results. However, to determine accurate and reliable values for energy, a higher basis set is necessary.

The Diels Alder Cycloaddition

The Diels Ander reaction is a type of pericyclic reaction between a cis-diene and dienophile called a cycloaddition reaction, and is often refered to as a [4+2] commenting on the number of atoms involved. A cycloaddition reaction results in the breaking of 3 π bonds and 1 σ bond to form 1 π bond and 2 σ bonds, this is thermodynamically more favourable.

The reaction is dependent on the interaction between the HOMO and LUMO to form two new bonding and anti-bonding orbitals, this interaction is described by frontier orbital theory. The greatest HOMO-LUMO interaction occurs between an electron rich diene (contains an electron donating substituent) and electron poor dienophile (contains an electron withdrawing substituent. Reaction between an electron poor diene and and electorn rich dienophile can occur but this is not facile and requires a catalyst, a reaction of this type is known as inverse electron demand.

The principle orbital interactions can be classified as symmetric or anti-symmetric with respect to a plane of symmetry. By interpreting the nodal properties of the HOMO and LUMO, it is possible to determine if a reaction is allowed or forbidden. Programs such as GaussView can be used to generate representations of the molecules orbitals (MOs) of molecules. Experimentally this is a useful technique as it can be computed whether a reaction will occur, minimising the need for trial and error in a laboratory.

(Good intro, but you need to proofread as there are several typos Tam10 (talk) 18:15, 3 December 2015 (UTC))

Diels Alder between Ethylene and cis-Butadiene

Reaction Mechanism for the Diels Alder Reaction between cis-Butadiene and Ethylene

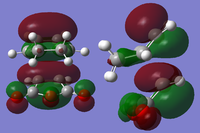
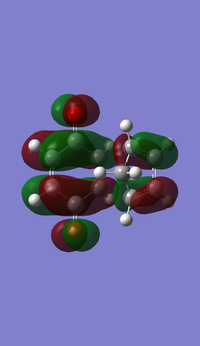
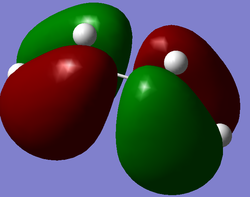
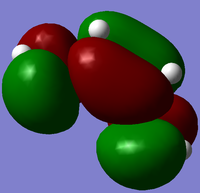
The cis-butadiene and ethylene were modeled on Gaussview then optimised at the AM1 semi-empirical method to compute representations of the MOs. The HOMO of cis-butadiene is anti-symmetric with respect to the plane; looking at the orbital representation, there is no plane of symmetry. The LUMO of cis-butadiene is symmetric; looking at the orbital representation, there is a plane of symmetry perpendicular to the C2-C3 bond.

Optimised Molecule	HOMO	LUMO

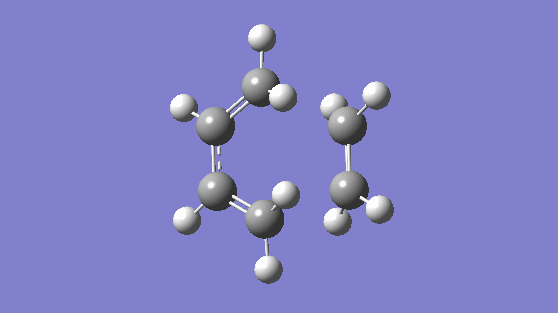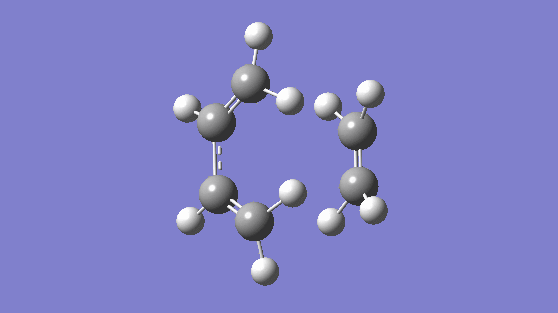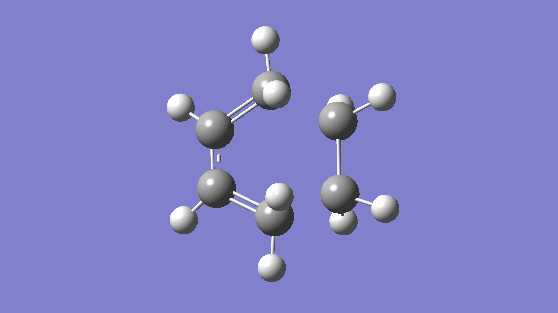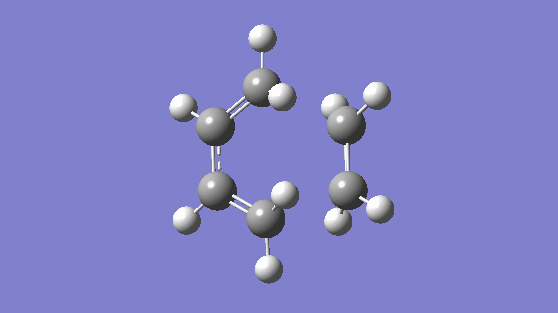
The transition state was modeled using the "Freeze-Coordinates"/"Bond Derivative" method using the HF/3-21G level of theory. This gave rise to the transition structure with a frequency of -818.36 cm^-1, this gives a synchronous vibration, and a lowest positive frequency of 166.53 cm^-1, this gives vibration which is not synchronous nor is asynchronous but it would not result in bond formation. The synchronous vibration animation of -818.36 cm^-1 gives rise to bond formation. To confirm the structure is in fact a transition state, an IRC is computed.

Vibration at Frequency 818.36 cm-1	Vibration at Frequency 166.53 cm-1

sp³ C-C bond lengths are typically 1.54 ‎Å, sp² C=C bond lengths are typically 1.34 ‎Å and the van der Waals radius of Carbonis 1.7 ‎Å . The bond of the partially formed C-C bonds in the transition structure are smaller than twice the van der Waals radius hence the Carbon atoms are in close proximity so the HOMO and LUMO are able to interact.

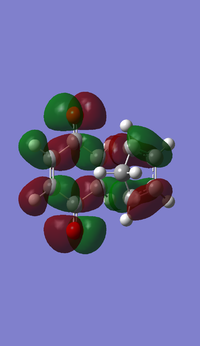
Representations of the MOs were obtained by an AM1 Semi-empirical optimisation of the final transition structure to obtain the HOMO and LUMO MOs. The HOMO of the transition structure is anti-symmetric and appears to have been formed by the HOMO of cis-butadiene and the LUMO of ethylene. The LUMO is symmetric with respect to the plane; the LUMO appears to have been formed by the LUMO of cis-butadiene and the HOMO of ethylene.

GaussView Structure	HOMO	LUMO	Bond Length /‎Å		Dehedral Angle /°
			C1-C2 = C3-C4	1.37002	C1-C2-C3	121.475
			C2-C3	1.39436	C2-C3-C4	121.463
			C4-C5	2.20889	C3-C4-C5	101.576
			C5-C6	1.37594	C4-C5-C6	109.154
			C6-C1	2.21080	C6-C1-C2	109.119

Regioselectivity of the Diels Alder Reaction

The reaction between cyclohexa-1,3-diene and maleic anhydride will be used in this section to examine the regioselectivity of Diels Alder reactions. This a a normal electron demand reaction. The reaction is able to yield two different products; an endo product and an exo product. The endo product the kinetic product and is preferred over the exo product. The exo product is the thermodynamic product and is formed irreversibly, however its formation only occurs if there is a long reaction time.

(Is there a reference to back these statements up? Tam10 (talk) 18:15, 3 December 2015 (UTC))

The Diels Alder Mechanism between Cyclohexa-1,3-diene and Maleic Anhydride

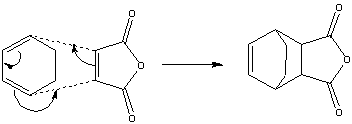
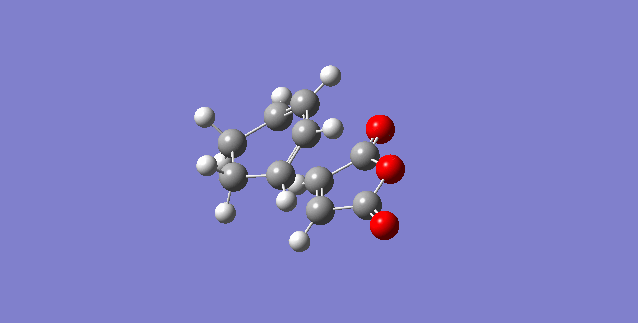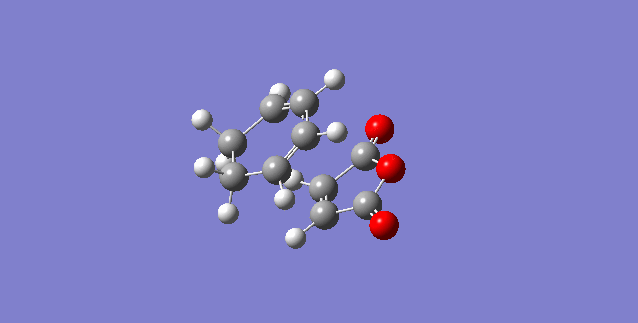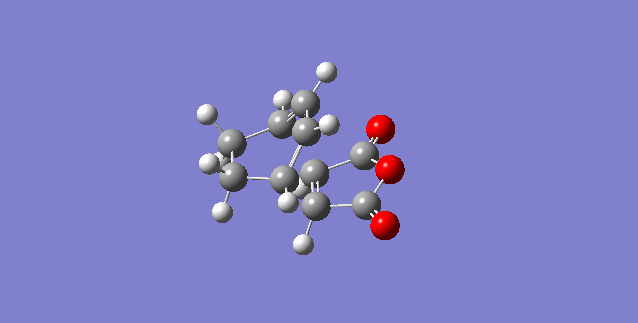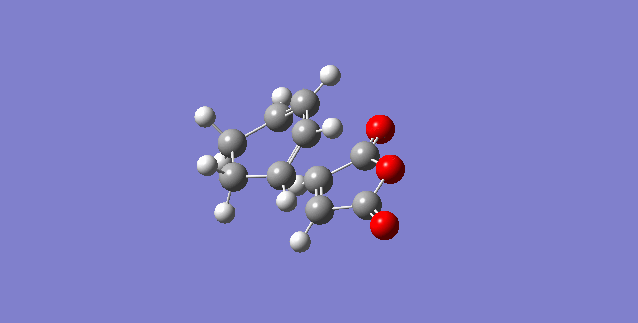
First the reactants were optimised to a DFT B3LYP/6-31G* level of theory because it is the least approximate and would give the highest level of accuracy, hence providing the most accurate representation. The cyclohexa-1,3-diene is the diene and the maleic anhydride is the dienophile, the oxygen atoms withdraw electron density from the C=C bond.

Cyclohexa-1,3-diene	Maleic Anhydride

Using the optimised reactant structures, they were aligned to form a structure similar to the transition state structures of the endo and exo products. By freezing the reacting carbon atoms, ensures that the optimisation does not vary the structure, hence still remaining in a form which the orbitals are able to interact to form the product. The "frozen" optimised chk file is then set to bond derivative and optimised again to determine the transition structure. This was carried out twice, once for the exo-adduct and once for the endo-adduct. The presence of a transition structure was confirmed by the computation of an IRC.

The Exo- Transition Structure

GaussView Animation	HOMO -1	HOMO	LUMO	LUMO +1	LUMO +2	Energy /Hartree
						-605.60505960
Increased steric hindrance between the ring structure and oxygen atoms on maleic anhydride. Secondary orbital overlap does not tend to occur in the exo-adduct to stabilise it	Cyclohexa-1,3-diene = symmetric Maleic anhydride = symmetric No secondary orbital overlap in this orbital.	Cyclohexa-1,3-diene = anti-symmetric Maleic anhydride = anti-symmetric No secondary orbital overlap in this orbital.	Cyclohexa-1,3-diene = anti-symmetric Maleic anhydride = anti-symmetric No secondary orbital overlap in this orbital.	Cyclohexa-1,3-diene = symmetric Maleic anhydride = symmetry No secondary orbital overlap in this orbital.	Cyclohexa-1,3-diene = anti-symmetric Maleic anhydride = anti-symmetry No secondary orbital overlap in this orbital.

The Endo-Transition Structure

GaussView Animation	HOMO -1	HOMO	LUMO	LUMO +1	LUMO +2	Energy /Hartree
						-605.61036819
Reduced steric hindrance. Secondary orbitals interactions between the LUMO of the dienophile and the HOMO of the diene tend to stabilise the endo-adduct.	Cyclohexa-1,3-diene = symmetric Maleic anhydride = symmetry No secondary orbital overlap in this orbital.	Cyclohexa-1,3-diene = anti-symmetric Maleic anhydride = anti-symmetry No secondary orbital overlap in this orbital.	Cyclohexa-1,3-diene = anti-symmetric Maleic anhydride = anti-symmetry No secondary orbital overlap in this orbital.	Cyclohexa-1,3-diene = symmetric Maleic anhydride = symmetry Secondary orbital overlap is present in this orbital.	Cyclohexa-1,3-diene = anti-symmetric Maleic anhydride = anti-symmetry Secondary orbital overlap is present in this orbital.

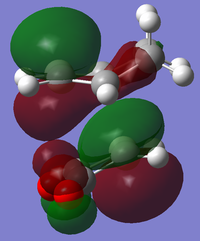
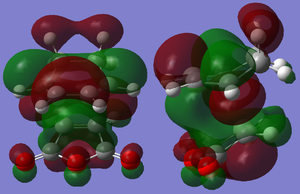
(This is a nice presentation of your data. However, I don't agree with your secondary orbital analysis. There will probably be too little interaction in the LUMO+1 to cause any stabilisation. Secondary orbital overlap should only be present in the HOMO or LUMO. If you look at MA and CHD separately, you should see the additional density on the sp2 hybridised carbons on MA (neighbouring the oxygens) which can interact with the diene system, and especially as the diene is converted to an alkene.

In the endo-adduct there are some secondary orbitals interactions in addition to primary orbital interactions. Whereas, in the exo-adduct there are no secondary orbitals interactions and only primary orbital interactions. Secondary orbital interactions results in an increases stabilisation factor. The combined effects of steric interactions and orbital interactions strongly suggests the endo transition state structure is preferred, this can be confirmed by calculation of the activation energies.

Activation Energies

The activation energies were calculated as before, using the energy values from an AM1 Semi-empirical calculation. The activation energies at 0 K were calculated using the sum of the electronic energy and zero point energy, the activation energies at 298.15 K were calculated using the sum of electronic and thermal energies. From these activation energies it is clear that the endo-adduct is formed through a lower energy barrier, hence this is the kinetic product and preferred. According to this data, the difference in activation barriers between the exo and endo transition structures is not very large, hence the exo product can be formed but this is not as facile as the formation of the endo product.

	Cyclohex-1,3-diene	Maleic Anhydride	Exo	ΔE(Exo) 0 K	ΔE(Exo) 298.15 K	Endo	ΔE(Endo) 0 K	ΔE(Endo) 298.15 K
Energy /Hartree	0.02771129	-0.12182418	-0.15990924	0.198226	0.203072	-0.05150480	0.19684	0.20182883
Energy /kcalmol-1	17.389	-76.457	-100.344	124.389	127.4	-32.320	123.519	126.649

(I'm a little confused by this table. To begin with, you have converted absolute energies into kcal/mol. I don't know how you calculated your energies and it looks like you have the exo product energy under "Exo" and the endo TS energy under "Endo" Tam10 (talk) 18:15, 3 December 2015 (UTC))

Conclusion

From this investigation using GaussView 5.0.9, the difference levels of theory have been examined then using appropriately to compute physical properties for the Cope Rearrangement and the Diels Alder Cycloaddition.

The tutorial with the Cope Rearrangement allowed familiarisation of the software and the theory. Methods for obtaining the transition state were experimented with to determine the best method, personally, the frozen coordinate method worked best as a structure close to the transition structure was obtained. This structure's similarity to the transition structure was examined using the intrinsic reaction coordinate (IRC) which mapped the path to the lowest energy geometry. Having calculated the transition structure and optimised it, a frequency calculation was then used to compute the physical properties which were then used to calculate activation energies. Activation energies provide a wealth of information on the feasibility of reactions and the reaction kinetics, particularly in the Arrhenius equation.

$k=\frac{k_{B}T}{h}{e}^{-\frac{\mathrm{\Delta }{G}^{‡}}{RT}}$

The next section used the knowledge gained from the tutorial to apply it to the Diels alder Cycloaddition. The reactants were modeled and used to compute the transition structure and its physical properties to prove why the endo-adduct is formed over the exo-adduct due to the reaction kinetics. The higher activation barrier of the exo-adduct means it is the thermodynamic product, hence is only likely to be formed when there is a longer reaction time.

It does need to be remembered that all the computational calculations do involve a large number of approximations, it is important to account for this before making conclusive decisions on a purely computational basis. An important interaction which has been ignored in these calculations electron-nuclei interactions, all the computations only consider the interaction of MO nodes. The Born-Oppenheimer Approximation has been applied which states that due to the size of the nuclei, it can be considered to be stationary hence does not impact upon electron distribution.