Rep:Mod:hb918
NH3 Molecule
NH3 Summary
| Feature | Result |
|---|---|
| N-H Bond Distance | 1.02 Å |
| H-N-H Bond Angle | 106o |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy E(RB3LYP) | -56.6 au |
| RMS Gradient | 0.00000485 au |
| Point Group of the Molecule | C3v |
Optimisation of NH3
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Jmol Image of NH3
Optimised Ammonia |
The optimisation file is linked here
Vibrations and Vibrational Modes
NH3 Vibrations
| Wavenumber (cm-1) | Symmetry | Intensity (arbitrary units) | Image |
|---|---|---|---|
| 1090 | A1 | 145 | 
|
| 1694 | E | 14 | 
|
| 1694 | E | 14 | 
|
| 3461 | A1 | 1 | 
|
| 3590 | E | 0 | 
|
| 3590 | E | 0 | 
|
• Based on the 3N-6 rule, we would expect that there are 6 vibrational modes (3(4) - 6 = 6).
• The data shows that there are 2 sets of degenerate vibrational modes. These occur at 1694cm-1 and 3590cm-1.
• The vibrations at 1090cm-1 and 1694cm-1 are bending modes and the vibrations at 3461cm-1 and 3590cm-1 are stretching modes.
• The vibrational mode at 3461cm-1 is highly symmetric.
• The mode at 1090cm-1 is known as the "umbrella" mode.
• In an experimental spectrum of gaseous ammonia we would expect to see 2 bands because the vibrational modes at 3461cm-1 and 3590cm-1 have very low intensities. The 2 visible bands in the spectrum would be produced from the vibrational modes at 1090cm-1 and 1694cm-1.
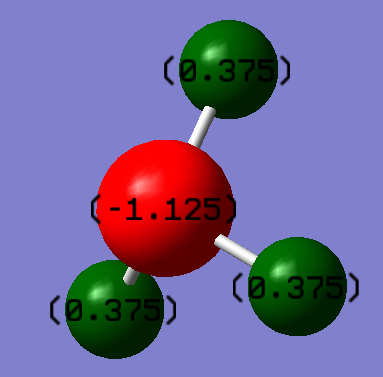
Charge Analysis
This image shows the NBO charge distribution for NH3
The N-atom has a charge of -1.125 D and the H-atoms have a charge of +0.375 D. We expect the N-atom to have a negative charge because it is the most electronegative atom in NH3 and this shows that the electron density mostly resides on the N-atom in the molecule.
N2 Molecule
N2 Summary
| Feature | Result |
|---|---|
| N-N Bond Distance | 1.11 Å |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy E(RB3LYP) | -109.5 au |
| RMS Gradient | 0.00013888 au |
| Point Group of the Molecule | D*h |
Optimisation of N2
Item Value Threshold Converged? Maximum Force 0.000241 0.000450 YES RMS Force 0.000241 0.000300 YES Maximum Displacement 0.000075 0.001800 YES RMS Displacement 0.000106 0.001200 YES
Jmol Image of N2
Optimised Nitrogen |
The optimisation file is linked here
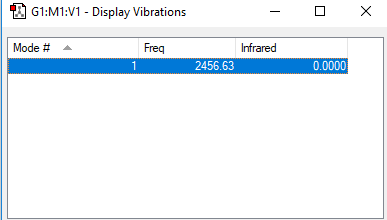
Vibrations and Vibrational Modes of N2
N2 Vibrations
| Wavenumber (cm-1) | Symmetry | Intensity (arbitrary units) | Image |
|---|---|---|---|
| 2457 | SGG | 0 | 
|
• To calculate the expected number of vibrational modes for a linear molecule, we use the 3N - 5 rule. This gives an answer of 3(2) - 5 = 1 vibrational mode. This vibrational mode is found at 2457cm-1.
Charge Analysis
This image shows the NBO charge distribution for N2
The charge on each N-atom is 0 D. We would expect the N-atoms to have a charge of 0 D because this molecule does not have a dipole as the electronegativity of each N-atom is the same, so there is equal charge distribution across the molecule.
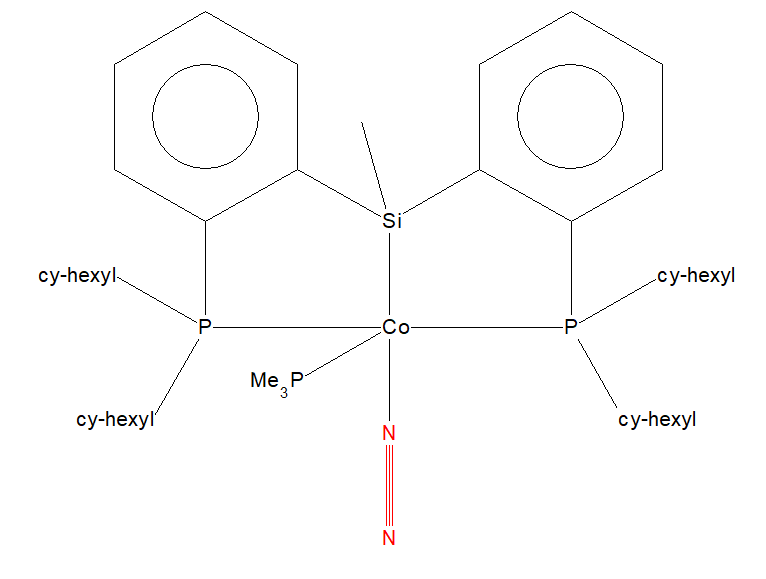
N2 Mono-Metallic TM Complex
Mono-Metallic TM Complex 2D Structure
N2 can bind to a metal ion in order to form a TM complex. The structure below is an example of a mono-metallic TM complex where the central cobalt ion coordinates to N2. This structure has an IUPAC name of (bis(2-(dicyclohexylphosphino)phenyl)(methyl)silyl)-dinitrogen-(trimethylphosphino)-cobalt. The unique identifier for this structure is VEJSEL. More information about this structure can be found [here]
Mono-Metallic TM Complex 3D Structure
3D VEJSEL |
This shows the 3D structure of the molecule. The N-atoms are depicted in blue.
Bond Properties
In the structure above, the N-N triple bond length obtained from Avogadro is found to be 1.13 Å. Using Gaussian, the bond length in an optimised N2 molecule is 1.11 Å. This difference in bond length shows that the VEJSEL N-N triple bond is weaker than expected. This is due to the fact that one of the N-atoms is coordinated to a cobalt metal ion and Co withdraws electron density slightly from the N2 triple bond and therefore also lowers the energy of this bond. This results in a longer bond length because the atoms are less tightly bound together. A difference in the bond lengths can also be due to the difference between computational and experimental methods for determining bond length. Computational methods involve the optimisation of the bond lengths to a fixed distance that places the molecule in the lowest energy state. Furthermore computational methods consider molecules in the gaseous state whereas experimentally the structure would be used in the solid state to determine bond length by X-ray diffraction.
Haber-Bosch Process
The Haber-Bosch process combines N2 and H2 to form ammonia. The overall reaction is given by the equation N2 + 3H2 → 2NH3.
E(NH3) = -56.55776873 au
2*E(NH3) = -113.115537 au
E(N2) = - 109.52412866 au
E(H2) = -1.17853934 au
3*(H2) = - 3.53561802 au
ΔE = 3*(H2) - (E(N2) + 3*(H2)) = -0.0557990 au
ΔE = -0.0557990 * 2625.5 = -146.500222 kJmol-1
ΔE = -146.5 kJmol-1
The energy change shows that this is an exothermic reaction because is it a negative energy change. Therefore the product (NH3) is more stable than the reactants (H2 and N2)
H2 Molecule
H2 Summary
| Feature | Result |
|---|---|
| H-H Bond Distance | 0.74 Å |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy E(RB3LYP) | -1.18 au |
| RMS Gradient | 0.00005659 au |
| Point Group of the Molecule | D*h |
Optimisation of H2
Item Value Threshold Converged? Maximum Force 0.000098 0.000450 YES RMS Force 0.000098 0.000300 YES Maximum Displacement 0.000129 0.001800 YES RMS Displacement 0.000182 0.001200 YES
Jmol Image of H2
Optimised Hydrogen |
The optimisation file is linked here
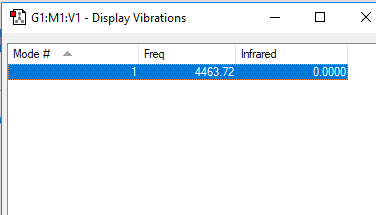
Vibrations and Vibrational Modes of H2
H2 Vibrations
| Wavenumber (cm-1) | Symmetry | Intensity (arbitrary units) | Image |
|---|---|---|---|
| 4464 | SGG | 0 | 
|
• Again, to calculate the expected number of vibrational modes for a linear molecule, we use the 3N - 5 rule. This gives an answer of 3(2) - 5 = 1 vibrational mode. This vibrational mode is found at 4464cm-1.
Charge Analysis
This image shows the NBO charge distribution for H2
Each H-atom has a charge of 0 D. This is because there is no dipole in the molecule, so there is an even charge distribution across the 2 H-atoms.
(Own Choice) CH4 Molecule
CH4 Summary
| Feature | Result |
|---|---|
| C-H Bond Distance | 1.07 Å |
| H-C-H Bond Angle | 109o |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy E(RB3LYP) | -40.5 au |
| RMS Gradient | 0.00003263 au |
| Point Group of the Molecule | TD |
Optimisation of CH4
Item Value Threshold Converged? Maximum Force 0.000063 0.000450 YES RMS Force 0.000034 0.000300 YES Maximum Displacement 0.000179 0.001800 YES RMS Displacement 0.000095 0.001200 YES
Jmol Image of CH4
Optimised Methane |
The optimisation file is linked here
Vibrations and Vibrational Modes
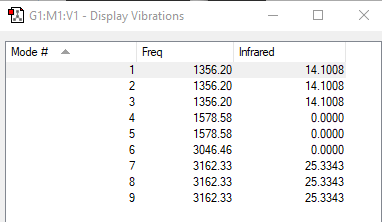
CH4 Vibrations
| Wavenumber (cm-1) | Symmetry | Intensity (arbitrary units) | Image |
|---|---|---|---|
| 1356 | T2 | 14 | 
|
| 1356 | T2 | 14 | 
|
| 1356 | T2 | 14 | 
|
| 1579 | E | 0 | 
|
| 1579 | E | 0 | 
|
| 3046 | A1 | 0 | 
|
| 3162 | T2 | 25 | 
|
| 3162 | T2 | 25 | 
|
| 3162 | T2 | 25 | 
|
•Using the 3N - 6 rule, we would predict that there are 3(5) - 6 = 9 vibrational modes.
•The 3 vibrations at 1356 (cm-1) are degenerate, the 2 vibrations at 1579 (cm-1) are degenerate, and the 3 vibrations at 3162 (cm-1) are degenerate.
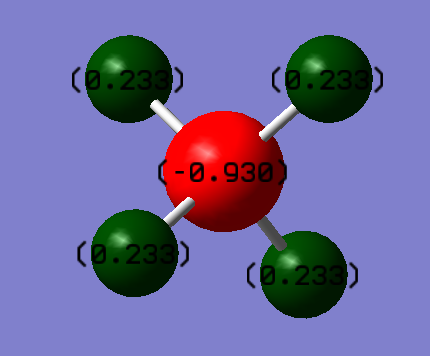
Charge Analysis
This image shows the NBO charge distribution for CH4
The C-atom has a charge of -0.93 D and the H-atoms have a charge of 0.233 D. We expect the carbon atom to have a negative charge because it is the most electronegative atom in CH4 and this shows that the electron density mostly resides on the C-atom in the molecule.
CH4 Molecular Orbitals
| Image | Energy | Description |
|---|---|---|
 |
-10.16707 | This orbital is the 1s orbital located on the carbon atom. It is much lower in energy than the other orbitals as it is tightly bound to carbon and it is very stable. It is deep in energy. As it is the 1s orbital, the electrons in this orbital are found very close to the nucleus which is the reason for its stability. This orbital is filled with 2 electrons, both electrons are from carbon. |
 |
-0.69041 | This orbital is the lowest energy bonding MO between the 2s orbital of carbon and the 1s orbital of hydrogen. As it is a bonding MO and it is filled with 2 electrons, it is involved in chemical bonding. |
 |
-0.38831 | This orbital is another filled bonding MO, it is one of 3 degenerate bonding MOs. It is formed from the combination of the 2p orbital on carbon and the 1s orbital of hydrogen. Each MO is perpendicular to each other. Only one is shown in the image. One of these is also the HOMO as each of these 3 degenerate MOs is filled with 2 electrons and this is the highest energy level occupied in CH4. |
 |
0.11824 | This is an empty antibonding MO. It is the lowest energy unoccupied MO and therefore it is the LUMO. As this antibonding orbital is unfilled, it has no effect on the chemical bonding within the molecule. |
 |
0.17677 | This is another empty antibonding MO. It is the antibonding MO formed from destructive interference of the carbon 2p and hydrogen 1s orbitals. There are 3 of these with the same energy and they are degenerate and perpendicular to each other. This is higher in energy than the HOMO/LUMO region. It is unfilled and has no effect on the chemical bonding within the molecule. |
(Independent Work) HCN Molecule
HCN Summary
| Feature | Result |
|---|---|
| C-N Bond Distance | 1.16 Å |
| C-H Bond Distance | 1.07 Å |
| H-C-N Bond Angle | 180o |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy E(RB3LYP) | -93.4 au |
| RMS Gradient | 0.00017006 au |
| Point Group of the Molecule | C*V |
Optimisation of HCN
Item Value Threshold Converged? Maximum Force 0.000370 0.000450 YES RMS Force 0.000255 0.000300 YES Maximum Displacement 0.000676 0.001800 YES RMS Displacement 0.000427 0.001200 YES
Jmol Image of HCN
Optimised HCN |
The optimisation file is linked here
Vibrations and Vibrational Modes
HCN Vibrations
| Wavenumber (cm-1) | Symmetry | Intensity (arbitrary units) | Image |
|---|---|---|---|
| 767 | PT | 35 | 
|
| 767 | PT | 35 | 
|
| 2215 | SG | 2 | 
|
| 3480 | SG | 57 | 
|
• Using the 3N-5 rule we woudl expect there for be 3(3) - 5 = 4 vibrational modes.
•The vibrational modes at 767 cm-1 are degenerate and they are bending modes.
•The modes at 2215 cm-1 and 3480 cm-1 are stretching modes.
Charge Analysis
This image shows the NBO charge distribution for HCN
The H-atom has a charge of 0.234 D, the C-atom has a charge of 0.073 D, and the N-atom has a charge of -0.308 D. We expect the N-atom to have the most negative charge because it is the most electronegative atom in the molecule. We expect the C-atom to be less positively charged than the H-atom because C is more electronegative than H. Electron density mostly resides on the N-atom
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 0.5/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES, overall this is a well structured wiki. However a lot of your images are very oversized and prevent the reader from seeing them with the other information on the page for context.
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES
N2 and H2 0.5/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 4/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
YES, overall good explanations on both MOs and charges. The MO discussion is also very well formatted, with appropriately sized images allowing the reader to compare the MOs. To improve the discussion you could have explained that the LUMO is the antibonding counterpart to MO2, and included its atomic contributions. Well done for recognising that unoccupied MOs do not effect the bonding.
Independence 1/1
If you have finished everything else and have spare time in the lab you could:
Check one of your results against the literature, or
Do an extra calculation on another small molecule, or
Do some deeper analysis on your results so far
You did an extra calculation and charge analysis on HCN, well done!