Rep:Mod:haz9

The Hydrogenation of Cylopentadiene Dimers

Dimerisation

The Dimerisation of Cyclopentadiene

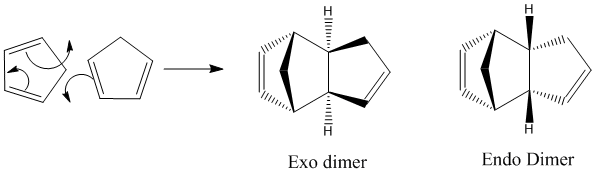
Cyclopentadiene dimerises to form an endo dimer product in preference to an exo dimer. Investigation of the energies of the two dimers reveals whether the reaction is under thermodynamic or kinetic control. Energy calculations were carried out using ChemBio 3D by optimising the geometry and using the MM2 force field option to determine which product is the least thermodynamically hindered and hence lowest in energy. The results are shown in the table below.

	Endo Dimer	Exo Dimer
Energy (kcal/mol)	34.00	31.88

Diagram to Show Orbital Interactions Resulting in Endo Preference

The exo product is lower in energy, i.e. more thermodynamically stable than the endo form. This means that if the reaction were under thermodynamic control, the reaction would favour the formation of the exo form. Experimentally this is shown not to be the case therefore, it can be concluded that the reaction is under kinetic control. The stability of the transition state must be the most important factor in determining the stereochemistry of the product.

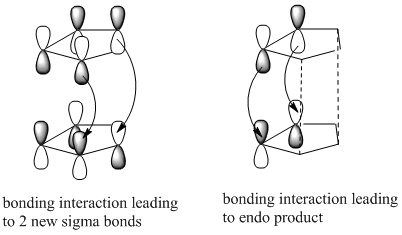
The dimerisation of cyclopentadiene is a [4+2] cycloaddition, in other words a Diels Alder reaction. Diels Alder reactions proceed kinetically and the stereochemistry of the product is determined by the approach of the dienophile and the diene. Generally the endo product is favoured in Diels Alder reactions according to the endo rule. The endo form is preferred due to the non-bonding interaction between the antibonding p orbitals at the back of the diene as well as the bonding interactions leading to the formation of the 2 new bonds. See the diagram adjacent:

Hydrogenation

Hydrogenation of Cyclopentadiene Dimer

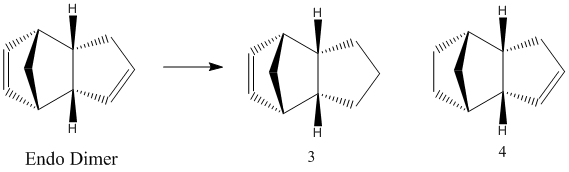
The endo product of the dimerisation may then undergo partial hydrogenation to form a dihydro derivative. The preferred stereochemistry of the dihydro derivative may be determined using ChemBio 3D. The two potential dihydro derivatives (labelled 3 and 4 in the diagram) were analysed in terms of their thermodynamically hindrance.

	Product 3	Product 4
Stretching	1.27	1.10
Bending	19.85	14.51
Torsion	10.81	12.50
Van de Waals	5.64	4.51
Dipole/dipole	0.16	0.14
Energy (kcal/mol)	35.69	31.15

Product 4 has the lowest total energy (by 4.54 kcal/mol) and it can therefore be concluded that product 4 is the thermodynamic product and product 3 is the kinetic product. Therefore, providing there is enough thermal energy provided to overcome the activation barrier, the reaction will preferentially form product 4. It can be concluded that the ease of thermodynamic hydrogenation of the double bond in the cyclohexene ring is greater than for the double bond in the cyclopentadiene ring. The ease of hydrogenation is due to the higher torsional strain of the double bond in the cyclohexene ring and the higher bending energy in product 3.

Stereochemistry of Nucleophilic Additions to a Ryridinium Ring

Reaction 1

Alkylation of the 4-position in Optically Active Prolinol Derivative using Methyl Magnesium Iodide

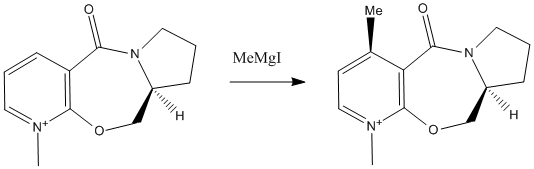
In reaction 1, prolinol is alklyated by MeMgI. The reaction is regio and stereoselective; the alkyl group is added to the top face of the molecule only. ChemBio3D was used to construct a model of the pyridine reactant (the MeMgI component could not be included in the calculations due to the parameters of the programme being unsuited to Mg atoms). The energy of the model was then minimised using the MM2 force field. The models were varied systematically before minimisation, focussing in particular on the conformations of the 5 and 7-membered rings. The 5 membered ring must always be up relative to the aromatic ring system which must always be planar therefore only the ring buckle in the 5 membered ring and the oxygen in the 7-membered ring may be varied in their position relative to the plane of the ring resulting in 5 possible conformations. The results are shown in the table below:

	Conformer 1	Conformer 2	Conformer 3	Conformer 4	Conformer 5
5 membered ring buckle	above plane	above plane	below plane	below plane	in the plane
Ring bound oxygen atom	above plane	below plane	above plane	below plane	in the plane
Energy of molecule (kcal/mol)	44.18	43.88	43.76	42.80	42.85
Dihedral angle of carbonyl group to aromatic ring	35.9	21.4	19.3	10.9	16.5

Lowest conformation structure
Lowest Energy Conformation of the Prolinol Derivative

Mechanism for alkylation of the 4-position in Optically Active Prolinol Derivative using Methyl Magnesium Iodide including chelation by carbonyl oxygen

The above image shows the lowest energy conformation of the pyridine ring system. As can be seen from the table, the highest energy conformations were the two which had the ether oxygen and the ring buckle on different sides of the plane. In each of the minimum energy conformations, the carbonyl oxygen sits slightly above the plane of the aromatic ring. This observation gives an insight into the mechanism of the alkylation reaction; the carbonyl oxygen must play a role in the mechanism namely by chelation. Oxygen may coordinate with the magnesium atom in a grignard reagent resulting in a weakening of the Mg-R bond, activating the Grignard for attack at the carbon most ideally positioned for maximisation of this interaction. In this case, the most ideal position for attack is the top face at the 4 position in the pyridine ring due to the position of the carbonyl in the ring system as detailed above.

Reaction 2

Diastereoselective addition of an N-Phenyl group onto the 4-position of the pyridinium ring in a quinolium salt using Aniline

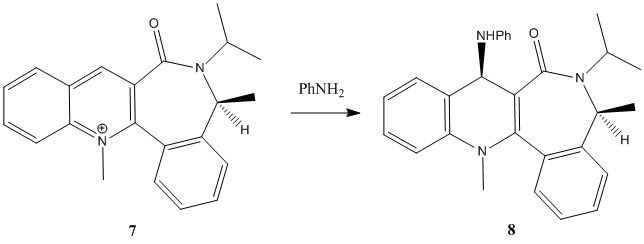
Compound 7, a quinolium salt undergoes addition of an N-Phenyl group onto the pyridine ring regio and stereoselectively as shown in the reaction scheme above. In order to determine the most energetically stable form of the pyridine reactant, a model was constructed in ChemBio 3D and minimised as before. It can be assumed that there is not much movement within the seven membered ring as proposed in the literature for Reaction 1. In fact, there will be even less movement possible due to the greater conformational lock effect of the extra phenyl group in reactant 7 as compared to the cyclopentane ring in reactant 5.

The lowest energy conformations have the carbonyl below the plane of the ring. This agrees with the literature proposition that it is the carbonyl dihedral angle which causes the 1,4 diastereoselective control. The reason for this is explained in the mechanism below:

Steric hindrance means carbonyl position below the ring is favourable

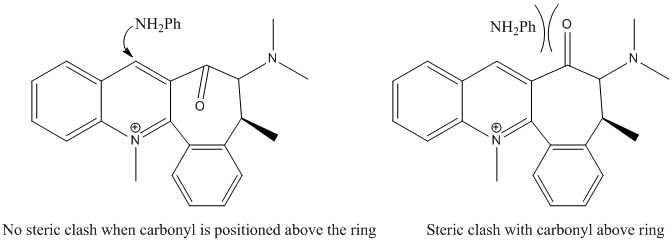
The position of the carbonyl on the bottom face of the quinolinium salt directs the attack of the amide to the top face of the ring due to steric repulsion of the phenyl group and the carbonyl oxygen.

Lowest conformation structure

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Two confomers of a key taxol intermediate

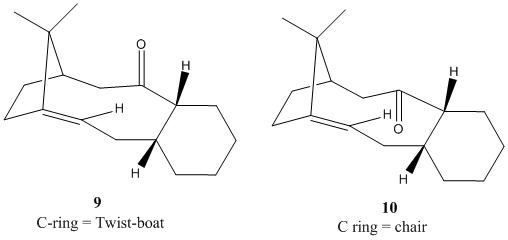
One of the key intermediates in the overall synthesis of Taxol has stereochemistry with the carbonyl group directed either above or below the plane of the ring. The intermediate has the ability to show atropisomerism due to the steric hindrance of free rotation around the carbon-carbon bond alpha and beta to the carbonyl group caused by the rigidity imposed by the ring system. The predominant stereochemistry of the intermediate is inevitably dependent on the relative energy of the two intermediates. This was investigated using the MM2 forcefield in ChemBio 3D. The conformer with the lowest energy will be the most predominant. As can be seen from the table below, conformer 10 is the most stable so it will be the major product. The relative stability of the chair conformer is presumably due to an elimination of steric clashing between the carbonyl and the nearby methyl bridging carbon. The MMFF94 field produces different energy values but the difference in the energy values remains similar. There is a difference of 4.4 kcal/mol for the MM2 field and a difference of 4.23 kcal/mol for the MMFF94 field.

	Conformer 9 (twist-boat)	Conformer 10 (chair)
MM2 Minimisation Energy (kcal/mol)	53.20	48.88
Torsion (kcal/mol)	21.35	18.21
MMFF94 Minimisation Energy (kcal/mol)	74.78	70.55

Conformer 9	Conformer 10
Lowest conformation structure	Lowest conformation structure

The alkene in the intermediate shows abnormal reactivity upon additional functionalisation; it will only hydrogenate to form an alkane very slowly. The olefin strain energy is defined as the difference in energy between the alkane and the alkene. Hyperstability is bestowed upon the alkene by the bridge head carbon at one of its ends. The strain from the rigid bridge head position will be greater in the alkane than in the alkene. The reaction from a stable flattened pyramidal structure to a strained tetrahedral structure will be unfavourable, i.e. the olefin strain energy will be negative.

Modelling Using Semi-empirical Molecular Orbital Theory

Regioselective Addition of Dichlorocarbene

In some cases, a purely mechanical molecular model approach is not enough to predict and explain the stereoselectivity of reactions, the distribution of electrons into molecular orbitals must be taken into account. In order to understand the regioselectivity of electrophilic addition to dichlorocarbene, the HOMO (the most reactive orbital to electrophilic attack) of the molecule must be examined in order to determine the relative reactivity of the two double bonds in the molecule. Thumbnail images of the frontier orbitals are shown below.

Firstly the energy of the molecule was minimised using the MM2 force field in ChemBio 3D. The minimised energy was 17.90 kcal/mol. The MOPAC/RM1 method was then used to minimise the energy, calculate the heat of formation (22.83 kcal/mol) and calculate the molecular orbitals of dichlorocarbene.

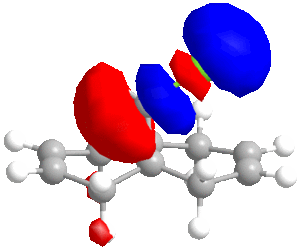
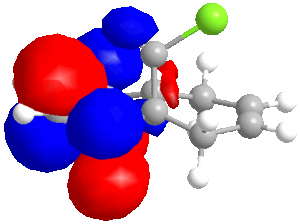
LUMO+2	LUMO+1	LUMO	HOMO	HOMO-1	HOMO-2

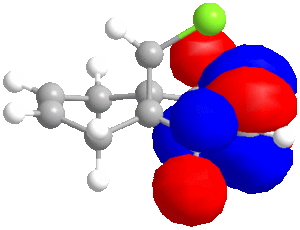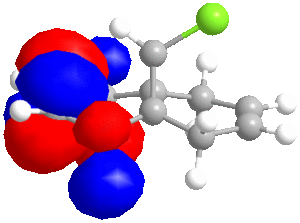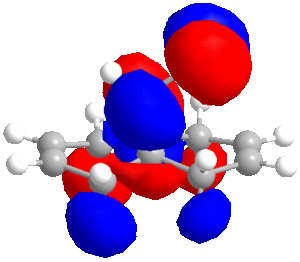As can be seen from the images above, the HOMO is mainly situated above one of the alkene bonds; the double bond underneath or endo to the chlorine atom. This means that it is this alkene double bond that will selectively undergo electrophilic addition, i.e. it is the more nucleophilic.

Dichlorocarbene and its hydrogenated monoalkene were then compared in order to determine the effect of the C-Cl

Mini-Project

One of the key things one must consider in organic synthesis is isomerisation. Isomerisation impacts on the most important aspects of synthesis for example the stereochemistry of the major product and purification to one isomer only. The stereochemistry of the product is extremely important, affecting everything from the physical properties to the reactivity of the compound. A product which contains a mixture of isomers can have disastrous effects, e.g. in the case of Thalidomide. Characterisation techniques which help determine the stereochemistry of the product include X-ray crystallography (if the product is a solid), UV and IR spectroscopy and NMR spectroscopy.

Isomerisation of methyl cis-cinnamate to methyl trans-cinnamate

In this mini-project, an example from recent literature was chosen and 13C NMR, J-coupling and IR spectroscopy will be used to help determine whether the product formed is the isomer purported in the journal. The reaction examined in this project is the “Palladium(II)-Catalysed Isomerisation of Olefins with Tributyltin Hydride”. This is a proposed reaction method by which geometrically pure (E)-alkenes are formed from aryl- or alkyl- substituted (Z)-alkenes using tributyltine hydride and triethylamine with catalytic palladium acetate. This method provides a mild, facile and efficient alternative to the preparation of carbon-carbon double bonds by schemes such as the Wittig reaction and olefin metathesis which can form a mixture of isomers as the product. The isomerisation was tested on various types of alkenes with different substituents. The nature of the substituent appeared to have a large effect on the percentage yield of the (E)-isomer versus the (Z)-isomer. Only one of the alkene isomerisations was chosen for investigation in this mini-project. This alkene yielded 98% of the (E)-alkene, this was attributed to the stabilisation of the carbocation intermediate provided by the phenyl substituent. The reaction scheme is shown adjacent:

Minimisation Energies

There were two possible conformations for the (E)-alkene proposed as the product. The phenyl group has to remain in the plane of the ring and the ester group must be orientated trans to the phenyl groups so it is only the ester group that has some degree of freedom around its bonds. The most stable form of the ester CH3-CO-O-CHPh is oriented such that the O=C-CH bond is antiperiplanar to the O-CH2Ph bond. The (E)-alkene was minimised in geometry and energy before NMR was calculated and the results are shown in the table below. Please note that the (Z)-alkene reactant was analysed alongside the (E)-alkene for comparison as the 2% minor product.

	(Z)-alkene	(E)-alkene
MM2 Minimisation Energy (kcal/mol)	19.78	7.88
MMFF94 Minimisation Energy (kcal/mol)	24.37	11.26
Lowest energy conformation	Lowest conformation structure	Lowest conformation structure

¹³C NMR Analysis

The ¹³C NMR was calculated for both alkenes using Gaussview 5.0. In order to determine whether the product obtained was in fact the (E) rather than the (Z)-isomer, the literature ¹³C NMR chemical shift values for the product were compared to the calculated chemical shift values for the (Z)-alkene and those of the (E)-alkene and then, for good measure, the literature values for the reactant (Z)-alkene were also compared in the same way. The literature only quotes 8 chemical shifts for the product instead of the 10 carbon atoms present in the molecule because it recognises the ortho and meta aromatic carbon environments as doubly degenerate whereas Gaussview did not. In order to compare the literature with the predicted ¹³C NMR spectra, the average of the two shifts in each environment was used. A systematic error of about 5 ppm occurs for carbonyls of esters. This was accounted for with a simple correction: δ_corr = 0.96δ_calc + 12.2. The square of the difference for each comparison was taken in order to obtain the magnitude of the difference for summation.

¹³C NMR for the (E)-alkene

¹³C NMR for the (E)-alkene

Product (E)-isomer	(Z)-isomer			(E)-isomer
Literature Values	Calculated Chemical shifts (ppm)	Adjusted Chemical shifts (ppm)	Square of the Difference Between (E)-alkene literature shifts and (Z)-alkene Calculated Shifts	Calculated Chemical shifts (ppm)	Adjusted Chemical shifts (ppm)	Square of the Difference Between (E)-alkene literature shifts and (E)-alkene Calculated Shifts
51.85	52.35	52.35	0.5	52.04	52.04	0.19
118.08	115.97	115.97	2.11	116.86	116.86	1.22
128.3	123.31	124.945	3.355	126.86	126.645	1.655
	126.58		0	126.43		0
129.11	126.68	127.825	1.285	129.07	129.5	0.39
	128.97		0	129.93		0
130.5	131.29	131.29	0.79	131.81	131.81	1.31
134.65	131.43	131.43	3.22	134.39	134.39	0.26
145.06	144.3	144.3	0.76	142.61	142.61	2.45
167.58	161.78	167.5088	0.0712	161.7	167.432	0.148
		Total Difference	12.0912		Total Difference	7.623
(Z)-isomer	(E)-isomer			(Z)-isomer
Literature Values	Calculated Chemical shifts (ppm)	Adjusted Chemical shifts (ppm)	Square of Difference Between (Z)-alkene Literature Shifts and (E)-alkene Calculated Shifts	Calculated Chemical shifts (ppm)	Adjusted Chemical shifts (ppm)	Square of Difference Between (Z)-alkene Literature Shifts and (Z)-alkene Calculated Shifts
51.58	52.35	52.35	0.77	52.04	52.04	0.46
119.56	115.97	115.97	3.59	116.86	116.86	2.7
128.28	123.31	124.945	3.335	126.86	126.645	1.635
	126.58		0	126.43		0
129.31	126.68	127.825	1.485	129.07	129.5	0.19
	128.97		0	129.93		0
129.94	131.29	131.29	1.35	131.81	131.81	1.87
135.04	131.43	131.43	3.61	134.39	134.39	0.65
143.59	144.3	144.3	0.71	142.61	142.61	0.98
166.82	161.78	167.5088	0.6888	161.7	167.432	0.612
		Total Difference	15.5388		Total Difference	9.097

From the table above, it can be seen that the literature chemical shifts for the product fit better with the (E)-alkene than the (Z)-alkene calculated spectra and the literature chemical shifts for the reactant fit better with the (Z)-alkene than the (E)-alkene. However, although the results fit the proposed structure in the literature, the differences between the chemical shifts in every comparison were all less than 5 ppm even for comparison with the wrong structure. The problem with this analysis is the differences between the structure in the ¹³C NMR are not perhaps great enough for a significant difference greater than the error on each of the calculations. As a result, no definite conclusion can be made about the stereochemistry of the product from ¹³C NMR; another type of analysis is needed.

¹H NMR Analysis

Although Gaussian can be used to calculate ¹³C NMR shifts, the technique is not sensitive enough to predict ¹H NMR spectra. However, Janocchio can be used to calculate coupling constants between hydrogen atoms. The most obvious difference between cis and trans-alkenes is the dihedral angle between the substituents on the carbon-carbon double bond. For 1,2-disubstituted cis-alkenes, the dihedral angle H-C=C-H should be around 0º and for 1,2-disubstituted trans-alkenes, the dihedral angle H-C=C-H should be around 180º. The dihedral angle around the double bond has significant effects on the ³J-coupling constants between the two hydrogens on the double bond in ¹H NMR according to the Karplus equation: J(ϕ) = A cos² ϕ + B cos ϕ + C where J is the coupling constant, ϕ is the dihedral angle and A, B and C are empirically derived parameters whose values but not relationship depend on the atoms and substituents involved. The relationship between dihedral angle and ³J-coupling constant is shown in the graph below:

Graph of the Karplus relation J(ϕ) = A cos² ϕ + B cos ϕ + C

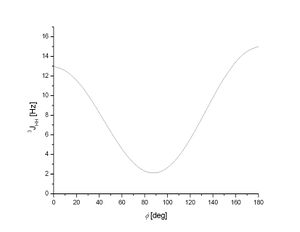
There is a minima at 90º torsion angle and J is large around both 0º and 180º. The value of J is largest at 180º, this is significant because it means that trans-alkenes have larger coupling constants than cis-alkenes. Therefore, an analysis of the ³J coupling constants can conclusively determine whether an alkene is cis or trans. The results are shown in the table below:

	(E)-alkene			(Z)-alkene
	H-C=C-H	Ph-C=C-H	H-C=C-C=O	H-C=C-H	Ph-C=C-H	H-C=C-C=O
Literature J values	15.6			12.9
Calculated J values	8.22	6.82	6.82	8.22	8.82	8.82
Dihedral angles (degrees)	-179.7	0.3	0.3	-0.1	179.9	179.9

As can be seen from the table above, the literature values and the calculated values for ³J-coupling constants are larger for the trans-alkene than the cis-alkene which supports the postulated stereochemistry of the trans-alkene product.

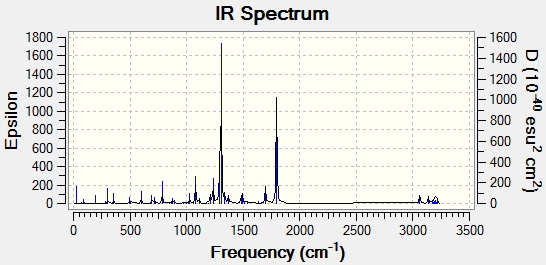
IR

IR is another computational method that could be used to discriminate between two isomers in the product. The IR spectra were recorded for both alkene isomers and the results are shown below. Unfortunately, no IR data was to be found in the journal even in the supporting information so no comparison could be made with literature.

Conclusions

Proposed Mechanism for Palladium Catalysed Isomerisation of Z-alkenes in Presence of Tributyl tin

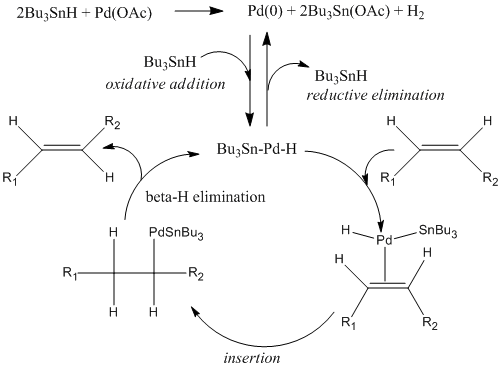
The most conclusive of all the evidence gathered for the correct identification of the product in the reaction chosen from the literature is the dihedral angle of the cis and trans-alkenes deduced from the literature J-coupling values matching with the calculated dihedral angles. The carbon NMR result did also prove the stereochemistry of the product was indeed trans but the difference between the two calculated spectra was smaller than the expected errors on the calculations. The reason for the highly stereoselective nature of this reaction is explained in the mechanism below: Firstly, metallic Pd (0) is generated by the reduction of palladium(II) acetate by tributyltin hydride. It is assumed that the Pd(0) thus formed serves as an active catalyst for the isomerization reaction. Next, oxidative addition of Bu₃SnH to Pd(0) affords a palladium-tin complex, which undergoes insertion. &beta-H elimination gives the thermodynamically stable (E)-olefin and Bu₃Sn-Pd-H 12, which regenerates Pd(0). Palladium hydride also serves as a catalytic species through insertion into the(Z)-alkene.