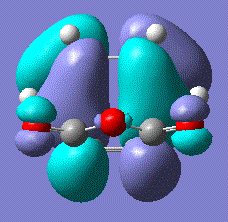
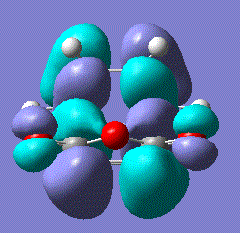
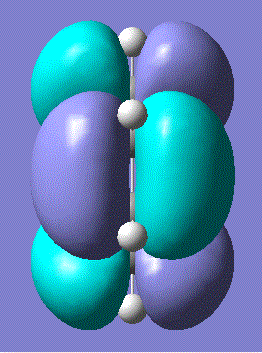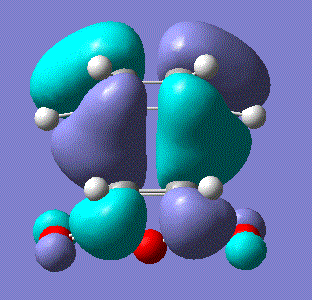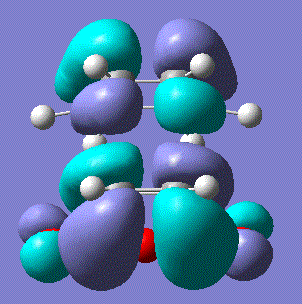Rep:Mod:haz11

Introduction

This experiment differs from the others carried out during this 3rd year computational lab course in that the transition states of molecules are being studied as oppose to the ground state structures. The mechanics/force field methods that were employed during other modules of this course cannot be used and instead molecular orbital-based methods must be used to numerically solve the schrodinger equation and locate the transition structures based on the local shape of a potential energy surface. These techniques are extremely useful in order to determine the structure of transition states, reaction path shapes and barrier heights.

The Cope Rearrangement Tutorial

Optimisation of the Reactants and Products

Three possible mechanisms for Cope rearrangement of 1,5-hexadiene

Transition States for Cope Rearrangement of 1,5-hexadiene

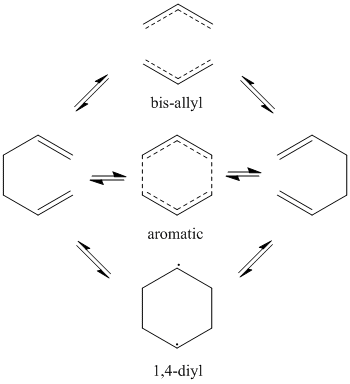
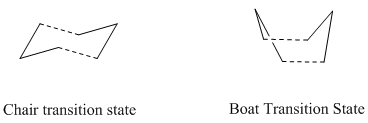
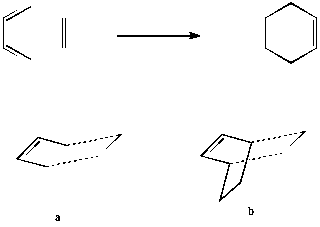
The focus of this exercise will be the Cope rearrangement of 1,5-hexadiene. The reaction proceeds via a [3,3]-sigmatropic shift but the mechanism (concerted, dissociative or step-wise) has been under debate for many years due to the differing conclusions of computational predictions arising from the relative flatness of the potential energy surface connecting the competing possible transition structures. In recent times, it has become accepted that the reaction is concerted and goes via either a "boat" or "chair" transition state (see diagram). The boat transition state is relatively higher in energy by several kcal/mol. The relative energies were calculated using the B3LYP/6-31G* method (which shows reasonable agreement with experiment for its calculatios of activation energies and enthalpies) in Gaussian. A molecule of 1,5-hexadiene was drawn in Gaussview 3.09 with anti linkage, that is an approximately antiperiplanar conformation for the central four carbon atoms. The structure was "cleaned" and then the HF/3-21G theory used to optimise the molecule. The results summary is shown in the table below:

Results Summary Table for App Conformer

File Type	log
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
E(RHF) (a.u.)	-232.69260235
RMS Gradient Norm(a.u.)	0.00001929
Dipole Moment (Debye)	0.2022
Point Group	C2

The same theory level and method were used optimise the structure of another conformer of the molecule with gauche linkage in order to determine which has the lowest energy. The results summary is shown in the table below:

Results Summary Table for Gauche Conformer

File Type	log
Calculation Type	FOPT
Calculation Method	RHF
Basis Set	3-21G
E(RHF) (a.u.)	-232.69266122
RMS Gradient Norm(a.u.)	0.00000743
Dipole Moment (Debye)	0.3048
Point Group	C1

It was expected that the gauche linkage conformer should have a higher energy than the antiperiplanar conformer due to the more favourable overlap of the same sized σ*_C-C and the σ_C-C orbitals in comparison to the less favourable overlap of the more different sized σ*_C-H and the σ_C-C and the σ*_C-C and the σ_C-H orbitals. However, as can be seen from the tables above, this was not the case, the Gauche conformer is in fact lower in energy. After comparison with the appendix table in the wiki (https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3#Appendix_1), it was found that the lower energy conformer drawn is in fact the Gauche 3 conformer which is the lowest energy conformer possible. The origin of this unexpected stability is due to the increase in the factor of the attractive Van der Waals forces which favour folding back of the chain as the chain increases in length. The linkage relationship between the 4 central carbon atoms is not the only factor in the stability of the conformer; the relative orientation of the =CH₂ group affects its also. For good measure, another gauche conformer was also optimised for comparison with the anti conformer. This second gauche conformer is thought to be less stable than the anti conformer for the reasons explained above and does not have the extra stabilisation of the gauche 3 conformer because of the lack of favourable Van der Waals forces from back-folding. A comparison of all the structures calculated with the appendix is shown below:

Conformer	Structure	Point Group	Literature Energy (Appendix) Hartrees HF/3-21G	Calculated Energy Hartrees HF/3-21G
Anti 1	Lowest conformation structure	C2	-231.69260	-231.69260
Gauche 3	Lowest conformation structure	C1	-231.69266	-231.69266
Gauche 4	Lowest conformation structure	C2	-231.69153	-231.69153
Anti 2	Lowest conformation structure	Ci	-231.69254	-231.69254

All of the calculated optimised energies exactly match those in the appendix. The anti2 conformer was reoptimised using the B3LYP/6-31G* level. The geometry and energies are compared in the table below:

Table to show difference in energy and geometry for two different methods of optimisation

Method	HF/3-21G	B3LYP/6-31G*
Energy	-231.69253526	-234.55971536
Geometry	Bond angles: 124°, 111°, 124°	Bond angles: 125°, 113°, 125°

As can be seen from the table above, the geometry and the energy have stayed relatively similar. The lower level basis set in this case is accurate enough for the energy calculation.

Optimisation of the "Chair" and "Boat" Transition Structures

Chair Transtion State

The Chair transition state was optimised using two different methods. Transition states are more difficult to optimise than to minimise because a prerequisite of the calculation is that the negative direction of the curvature (that is the reaction coordinate) is known. The first method used here had to be based on a reasonable estimation of the transition state geometry which was then used to compute the force constant matrix (the Hessian) in the first step of the optimisation. This Hessian was then updated at each step of the optimisation. The results of this method will only be reliable if the original estimated structure was close enough to the true structure.

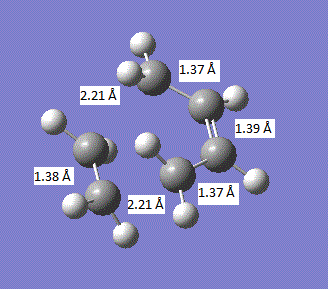
The structure was created by orientating two allyl fragments in a way reminiscent of the chair transition state as shown from the diagram in the appendix with the two fragments on top of one another with an approximate distance of 2.2 Å between the two sets of terminal carbons. The job Opt+Freq was selected with Optimization to a TS (Berry). The option to calculate the force constants once was chosen and the additional keywords "Opt=NoEigen" used. The results of the first method of optimisation are shown below:

Results Summary Table for 1st Optimisation of Chair Conformer

Bond Distances Å	2.02046
	2.02043
File Type	log
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
E(RHF) (a.u.)	-231.61932247
RMS Gradient Norm(a.u.)	0.00000398
Dipole Moment (Debye)	0.0001
Point Group	C2h

In order to determine whether the optimisation was successful, the frequency calculation must be examined to check whether there was an imaginary frequency at 818 cm_-1 corresponding to the Cope rearrangement. There was indeed a vibration at 818 cm_-1 and the animation is shown below:

Although the optimisation of the chair structure was successful, the transition state was optimised again using a method whereby firstly the reaction coordinate was frozen using Opt=ModRedundant whilst the rest of the molecule was minimised and then the reaction coordinate was unfrozen and the transition state geometry optimised again. This method does not necessarily need to compute the Hessian after this optimisation and may only need to differentiate along the reaction coordinate to guess the initial force constant matrix. The advantage of this method is that this can save time.

Results Summary Table for 2nd Optimisation of Chair Conformer

Bond Distances Å	2.20000
	2.32220
File Type	log
Calculation Type	FTS
Calculation Method	RHF
Basis Set	3-21G
E(RHF) (a.u.)	-231.61402307
RMS Gradient Norm(a.u.)	0.00605475
Dipole Moment (Debye)	0.0101
Point Group	C1

The energies were different

Boat Transition State

The boat transition structure was also optimised this time using the QST2 method. This method works by specifying the reactants and products for a reaction and then interpolating between the two structures to determine the transition state between them. The crucial part of the input of this calculation is that the reactant and products must be manually numbered so that the atoms correspond to each other in both structures. Even though both reactants and products are molecules of 1,5-hexadiene, the atoms have rearranged as shown in the diagram below: 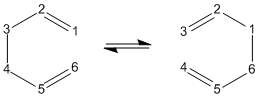The QST2 job was sent off but the job failed because the calculation did not rotate the top allyl fragment so the structure ressembles a dissociated chair-like structure. It was clear that the structures must be changed to be more boat-like in order for the calculation to find a reasonable transition state structure. The central C-C-C-C dihedral angle (C9-C1-C4-C7 in molecule 1 in the diagram below) was changed to 0° and the inside C-C-C angles (C9-C1-C4 and C7-C4-C1) changed to 100°.

Results Summary Table for Optimisation of Boat Conformer

Bond Distances Å	2.13995
	2.14012
File Type	log
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
E(RHF) (a.u.)	-231.602080232
RMS Gradient Norm(a.u.)	0.00003617
Dipole Moment (Debye)	0.1583
Point Group	C2v

In the frequency calculations, there was an imaginary vibration at -840 cm^-1 which corresponded to the Cope rearrangement

Intrinsic Reaction Coordinate Method

In order to determine which transition state connects which conformers of 1,5-hexadiene, the IRC method must be employed. This method creates a series of points by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest, i.e. up the slope towards the reactants or products. The IRC method was applied to the chair transition state which was optimised by the HF/3-21G level of theory. As the reaction coordinate is symmetrical, it need only be computed in one direction. The calculation was chosen to take 50 steps and the force constant to be calculated only once. The resulting structure was not a minimum, as the gradient was only 0.00218242 a.u. and the energy was -231.68052047 a.u. which means the IRC was not complete (see diagram).

Lowest conformation structure

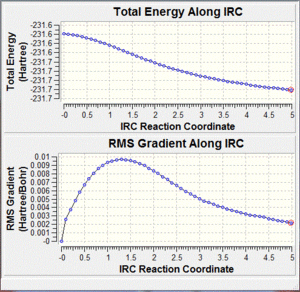Therefore, the last structure of the method was minimised and the energy was -231.69166702 a.u. and the gradient was 0.00000453 a.u. Interestingly, the structure of initial minimum and the final minimum were both Gauche 2 conformers. This means that the chair transition state is favoured by the 4th lowest energy conformer of 1,5-hexadiene.

The same IRC method was applied to the boat structure that was optimised in the above section.

Diels Alder Cycloaddition

In this section, the Diels Alder cyloaddition between cis-butadiene and ethene was investigated. Diels Alder reactions are pericyclic and involve the π orbitals of the diene and the dienophile which form new σ bonds between each other. Whether the reaction proceeds depends on the number of π-electrons involved. The reaction involves the HOMO/LUMO of the diene and the HOMO/LUMO of the dienophile. For the reaction to be allowed, the HOMO of one reactant must be able to interact with the LUMO of the other. For this to happen, the HOMO and LUMO must be of a similar energy and the same symmetry in order to have significant overlap density.

Subsituents on the dienophile may change the reactivity of the Diels Alder reaction, if the subsituents may interact with the new double bond formed in the product. In the first part of this exercise the transition state of the prototypical Diels Alder reaction will be investigated then in the second part, the transition state will be investigated for a reaction where both the diene and dienophile carry substituents. Below is an image of the prototype Diels Alder reaction and a suggested transition state structure:

Determining the Energy and Symmetry of the HOMO and LUMO

In the prototypical reaction, the principal orbital interactions involve the π/π* orbitals of ethene and the HOMO/LUMO of butadiene. The reaction is referred to as [4s+2s], this refers to the number of atoms in each of the diene and the dienophile respectively and the subscript refers to the symmetry (symmetric or antisymmetric) of the interacting orbitals with respect to the σ_v plane of symmetry perpendicular to the double bond in both reactants.

The table below examines the relative energy and symmetry of the HOMO/LUMO orbitals of the diene and the dienophile.

		HOMO			LUMO
Molecule	Energy of Molecule	Image of MO	Energy	Symmetry of MO w.r.t. σv plane	Image of MO	Energy	Symmetry of MO w.r.t. σv plane
Butadiene	-154.05394329		-0.325	Antisymmetric		0.123	Symmetric
Ethene	-77.60098737		-0.379	Symmetric		0.186	Antisymmetric

As can be seen from the table above, the HOMO of ethene and the LUMO of butadiene are both symmetric with respect to the reflection plane and the LUMO of ethylene and the HOMO of butadiene are both a. Thus it is the HOMO-LUMO pairs of orbital that interact, and energetically, the HOMO of the resulting adduct with two new σ bonds is a.

Computation of the Transition State Geometry for the Prototype Reaction and an Examination of the Nature of the Reaction Path

The transition structure of the prototype Diels Alder reaction is known and given in the lab script. The structure is envelope-like and maximizes the overlap between the ethene π orbitals and the π system of butadiene. As we have a reasonable postulate for the starting transition state structure, we can use the method whereby we optimise the structure to a T.S. (berry) and examine the frequency analysis for an imaginary frequency corresponding to the Diels Alder reaction. The product structure was built and optimised to obtain reasonable bond angles and lengths but then the product structure was altered so the -CH₂-CH₂- was removed from the main structure and the non-bonding distances were set to 2.2 Å (taking the same bond distances as in the optimisation of the chair transition structure). The resulting structure was obtained and is shown below along with the results summary of the opt+freq:

Lowest conformation structure

File Type	fch
Calculation Type	FREQ
Calculation Method	RHF
Basis Set	3-21G
E(RHF) (a.u.)	-231.60320857
RMS Gradient Norm(a.u.)	0.00000547
Imaginary Frequency	1
Dipole Moment (Debye)	0.5757

There was indeed an imaginary vibration at -818 cm^-1 which corresponded to the Diels Alder reaction, shown in the image below.

The vibration corresponds to the synchronous formation of the two bond as oppose to the lowest positive frequency at 166.53 which correpsonds to asynchronous bond formation. The HOMO and LUMO were sketched for the transition state and the results shown in the table below:

MO	Image	Symmetry	Energy
HOMO		Symmetric	-0.300
LUMO		Symmetric	0.142

These are slightly unusual results as the HOMO of the transition state was expected to be composed of the antisymmetric ethene LUMO and HOMO so we would expect it to be antisymmetric in order for it to be allowed. The LUMO of the transition state was indeed symmetric as expected if it was formed of the symmetric ethene HOMO and the butadiene LUMO.

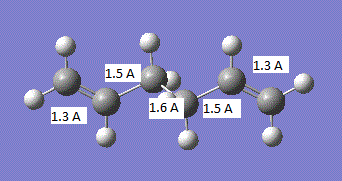
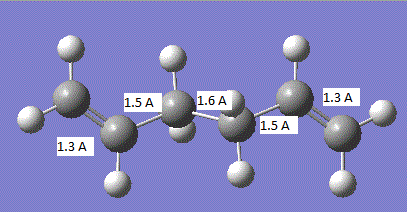
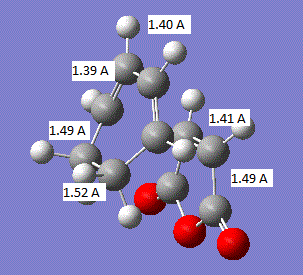
The geometry of the transition state is summarised in the image below:

It can be seen that all the carbon-carbon bonds are very close in length and the C-C-C bond in the cis butadiene is 121.5°. If we compare these values to the sp³ and sp² bond lengths, 1.54 A and 1.34 A respectively, we find that all the carbon-carbon bonds are closest to literature sp₂ hybridised bond lengths. In comparison to the van der Waals radius of the C atom of 1.7 A., all the bonds except those where the two new bonds are going to be formed are less than the van der waals radius and the two new bonds about to be formed are above the van der waals radius.

Study of the Regioselectivity of the Diels Alder Reaction

Cyclohexa-1,3-diene will react with maleic anhydride to form a primarily endo adduct. As the reaction should be under kinetic control, it is expected that the exo adduct will be higher in energy and therefore disfavoured. In this section of the exercise the transition structures for both the endo and the exo adduct were located and compared. A restricted AM1 method was used in the optimisation and frequency calculated. The frozen coordinate method was used to freeze the partly formed C-C distances to 2 A. The data was consolidated in the table below:

Property	Endo	Exo
Energy of Transition State (a.u.)	-0.05150478	-0.05041875
Imaginary Frequency in TS (cm-1)	-812	-806
Image to show imaginary frequency
Image to show bond lengths
Partly formed σ C-C bonds	2.16 A	2.17 A
Distance between the -(C=O)-O-(C=O)- of the maleic anhydride and the C atoms of the “opposite” -CH2-CH2-	2.89 A	2.95 A
HOMO energy	-0.345	-0.342
HOMO image
HOMO symmetry	antisymmetic	antisymmetric
LUMO energy	-0.035	-0.040
LUMO image
LUMO symmetry	antisymmetric	antisymmetric

As can be seen from the table above, the transition state with the lowest energy is the endo adduct which explains the regioselectivity of the endo product in the kinetically controlled diels alder reaction between maleic anhydride and cyclohexa-1,3-diene. The existence of this structure as a transition state is confirmed by one imaginary frequency for each of the transition states. The negative value of the frequency which is a second derivative of the optimisation curve confirms that the transition state is a maximum on the curve. The bond lengths within the two fragments are identical within two decimal places but the partly formed bond length is slightly longer in the exo transition state and the through space interaction between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” -CH2-CH2- for the exo is shorter than that between the fragment and the “opposite” -CH=CH- for the endo. The relatively shorter partly formed bond length is concurrent with the lower energy of the endo transition state but the shorter distance between the maleic anhydride and the opposite CH2-CH2 fragment indicates that steric repulsion between the fragments is not the only factor in determining the most stable conformation for the transition state.

The HOMO and LUMO were examined for each transition state to investigate the effect of secondary orbital interactions between the π systems of -CH=CH- and -(C=O)-O-(C=O)- fragment in the endo form. Both the HOMO and LUMO for both the transition states were antisymmetric which confirms our conclusions about allowed orbital overlap in the prototypical reaction investigation above.

Diagram to Show Orbital Interactions Resulting in Endo Preference

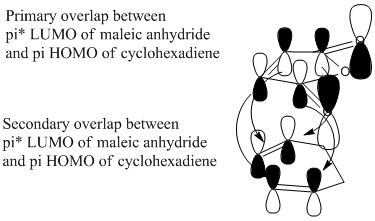
Diels Alder reactions proceed kinetically and the stereochemistry of the product is determined by the approach of the dienophile and the diene. Generally the endo product is favoured in Diels Alder reactions according to the endo rule. The endo form is preferred due to the non-bonding interaction between the antibonding p orbitals at the back of the diene as well as the bonding interactions leading to the formation of the 2 new bonds. See the diagram adjacent:

As can be seen from the images of the HOMO and LUMO above there are secondary orbital interactions due to the significant electron density between the -(C=O)-O-(C=O)- fragment in the endo form but not in the exo form. This stabilises the endo transition state relative to the exo transition state.