Rep:Mod:haz10

BH₃

Optimisation

An optimisation comprises two parts. The first part is known as the SCF (self consistent field) method or the Hartree-Fock method. This involves solving the Schrodinger equation for the electron density and the energy of a molecule for given positions of each of the nuclei. The second part of the optimisation requires moving the position of the nuclei and then repeating the SCF cycle at each permutation in order to determine which geometry has the lowest energy. The cycles continue until the forces converge, i.e. until the slope of the energy versus distance graph is close to zero and the energy at this point is taken as the lowest possible and the geometry is taken as the "optimised" geometry.

In order to solve the Schrodinger equation, the Born-Oppenheimer approximation must be employed whereby the nuclei are assumed to be so massive and move so slowly relative to the electrons which move instantaneously to follow them that their positions may be assumed to be fixed. The Schrodinger equation is solved to obtain an electron density and an energy which is dependent on the fixed positions of the nuclei. The energy and electron density of the molecule will inevitably vary according to the relative positions of the nuclei due to the electrostatic interactions between them. An optimisation may be thought of as a potential energy surface analogous to a bond dissociation diagram for a diatomic with the optimised energy of the molecule situated in the energy trough at the equilibrium bond distance. At each step of the optimisation the energy of the new configuration is compared to the last configuration and if the energy of the new configuration is less than that of the last configuration, then the optimisation moves in the same 'direction' along the potential energy surface. The cycle then starts again from this new lower energy configuration. The process assumes that the direction being followed is down the gradient of the potential energy well towards the optimised geometry.

If the nuclei and electrons are not in their equilibrium positions in the molecule, electrostatic interactions between them will act as forces upon them in order to shift them into more favourable positions. The molecule will experience these forces as long as a change in position has an associated change in energy. Therefore, force can be considered as the first derivative of energy, i.e. as the gradient of the energy versus nuclear position graph, the aforementioned potential energy surface. At equilibrium, there are no forces acting upon the nuclei and electrons and thus there is no change in energy associated with a change in r. This can be exploited by the optimisation methods which search for a structure for which the first derivative of the potential energy surface is zero.

These principles were demonstrated using a BH₃ molecule.

A molecule of BH₃ was created and then optimised using GaussView 3.09. The three B-H bond lengths were each set to 1.5 Å prior to optimisation. The optimisation method used was B3LYP and the basis set was 3-21G (a low accuracy basis set and therefore a quick calculation). The optimised BH₃ molecule was then opened as a log file and analysed. The information determined from the optimisation as well as an image of the optimised molecule are shown below:

Bond Length	1.19 Å
Bond Angles	30 °
File Type	log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	3-21G
E(RB+HF-LYP)	-26.46
Gradient	0.00000285
Dipole Moment	0.00
Point Group	D3h

Lowest conformation structure

The most important property to be examined is the gradient; if the optimisation is complete, the gradient will be close to zero, i.e. less than 0.001. For this optimisation, the gradient=0.00000285<0.001. Therefore, the optimisation can be deemed complete.

The "real" Gaussian output was examined as a text file in order to ascertain whether the job had finished by checking the final set of forces and displacements to see if the forces are converged, i.e. whether for a small displacement the energy changes or not. The relevant part of the file is shown below:

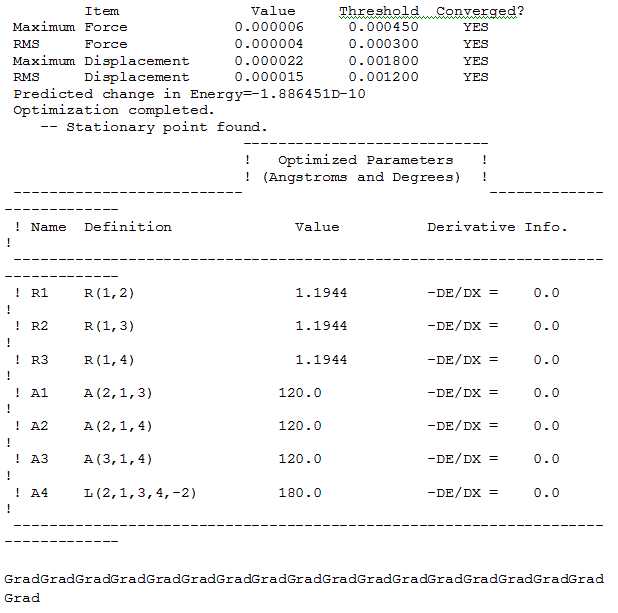
The convergence of the forces is important because force is the gradient of the energy vs distance graph. As can be seen from the image above, the forces and displacements have converged. This means that the electrostatic interactions between the nuclei and electrons are not causing forces to act upon the molecule to shift the nuclei into different positions which in turn means that the nuclei and electrons are in equilibrium and therefore there is no change in energy for a change in position.

Shown above is a graph of how the energy of the molecule varies at each step of the optimisation and a graph of how the gradient of the energy of the molecule varies at each step of the optimisation. As can be seen from the graphs, both the energy of the molecule and the gradient of the potential energy curve decreases as the optimisation proceeds.

The whole aim of an optimisation is to decrease the energy of the molecule until a minimum is reached and this is done in a step-wise fashion. This is clearly seen on the graph as the energy decreases from step 1-5. As described above, the energy of each geometry is compared to the last and if the new geometry has a lower energy than the last, then it is assumed that the direction followed is on the downwards slope of the PES heading towards the energy minimum. As a result, the graph resembles a one sided energy trough on a 2D PES.

The gradient of the graph will also decrease as it is the first derivative of the energy versus displacement and the change in energy will get smaller with change in displacement as the geometry moves closer to the equilibrium structure until the gradient reaches zero. The gradient is also related to the force as described above.

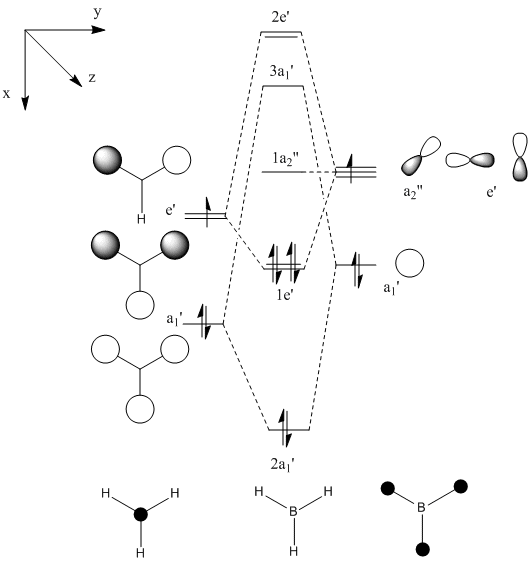
Molecular Orbitals of BH₃

The molecular orbitals were calculated using the previously optimised BH₃ molecule. The same method was used as before but this time the HPC servers were used to run the calculations instead of the laptop. The calculated molecular orbitals are shown below. The molecule is orientated in the same way for the images of each MO with one H atom pointing upwards reminiscent of a mercedes benz symbol. The Molecular orbital diagram is shown below. Note that the images of the molecular orbitals have been left out and are found in the table with the corresponding calculated molecular orbital. The link to the deposited completed population analysis is found here: http://hdl.handle.net/10042/to-6586

HOMO-3			LUMO
HOMO-2			LUMO+1
HOMO-1			LUMO+2
HOMO			LUMO+3

The calculated molecular orbitals match well with the qualitative molecular orbitals predicted by MO theory. The phase and symmetry of each molecular orbital is the same. There is a blending of lobes of the same phase to form one consolidated orbital but this is to be expected. In conclusion, it can be said that MO theory is a very useful qualitative analytical technique and that the method and basis set used in the optimisation of BH₃ were accurate enough given the size and number of the atoms. The approximations may begin to break down if the number of atoms increase or if the size of the atoms increase.

NBO Analysis of BH₃

The Natural Bond Orbitals of BH₃ were analysed using Gaussview and the log file from gaussian. The charge density of BH₃ was examined in Gaussview 3.09 by using a colour scale (red indicates negative charge and green indicates positive charge). The image is shown below:

The charge for the boron atom according to Gaussview is 0.331 and -0.110 for each of the three hydrogens. This is concurrent with the expected charge distribution of the molecule considering that boron is relatively electropositive in relation to hydrogen so the bonds are polarised with the majority of charge density residing on the hydride-like hydrogen atoms.

Vibrational Analysis of BH₃

Vibrational analysis can be used in order to confirm the optimised structure is the minimum on the PES. In order to determine the nature of a stationary point (where the first derivative is zero) as a minimum or a maximum, the second derivative must be taken and if it is positive, the stationary point is a minimum and if it is negative, the stationary point is a maximum. Frequency analysis is effectively taking the second derivative of the energy versus displacement graph. If the frequencies are all positive, the structure is a minimum, if one of them is negative then the structure is a transition state and if more than one calculated frequency is negative then we have failed to find a critical point and the optimisation is not complete or has failed.

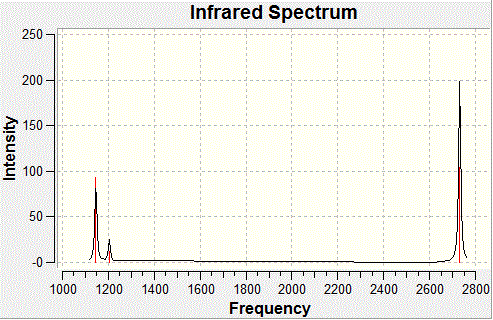
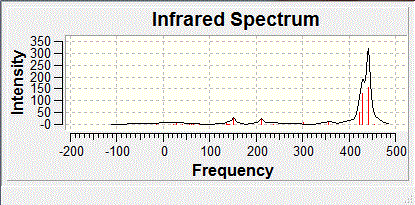
The same method as that used to optimise BH₃ was used to calculate the frequency of vibrations for the molecule. The summary energy for the molecule was -26.46, which means that the molecule is the same and hasn't deviated wildly to a different minimum on the PES. The predicted IR spectrum for BH₃ is shown below:

IR Spectrum for BH₃

Number	Form of the Vibration	Frequency	Intensity	Symmetry D3h Point Group
1		1146	93	a2
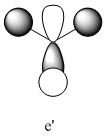
2		1205	12	e'
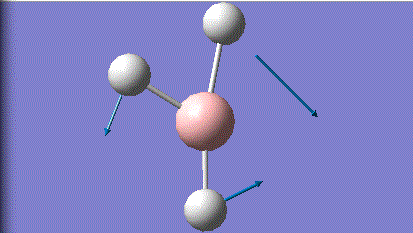
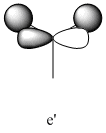
3		1205	12	e'
4		2593	0	a'1
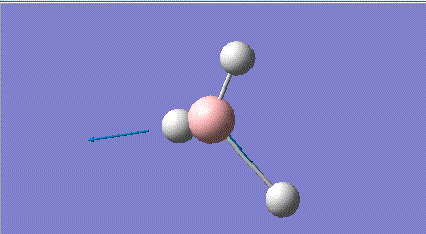
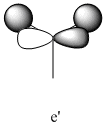
5		2731	104	e'
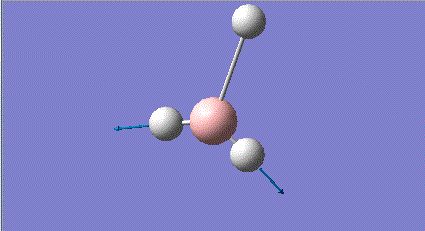
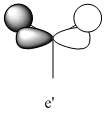
6		2731	104	e'

There is a discrepancy between the IR spectrum which shows 3 vibrational peaks and the frequency analysis which shows 6. This is because the peak at 2593 cm^-1 has 0 intensity as it is totally symmetric so has no overall dipole moment so it does not appear in the spectrum and then of the remaining 5 vibrations, there are two sets of degenerate vibrations which show up as one peak only for each pair.

TlBr₃

This section focuses on a molecule of TlBr₃ which is a much larger molecule than BH₃. Bromine is a third row element and has 35 electrons and Thallium is a 5th row element and has 81 electrons. Therefore, a larger basis set is required to compute the energy and electron density with respect to displacement, i.e. more dunctions need to be used to describe the electronic structure. The standard Schrodinger equation cannot account for the relativistic effects caused by the two elements. This is where a pseudo-potential comes in useful by recovering some of these relativistic effects. A pseudo-potential is a function that models the core electrons of an atom in order to make calculations easier by assuming that it is the valence electrons that dominate the reactivity of the molecule. The optimisation of TlBr₃ is an example where the real molecule is actually quite toxic so computational methods are very useful to minimise exposure to toxic substances.

A molecule of TlBr₃ was created and then optimised using DFT optimisation, the B3LYP method and the LanL2DZ basis set (a medium basis set). The results summary of the optimisation as well as an image of the optimised molecule are shown below:

Lowest conformation structure

Table to Show Properties of Optimised TlBr₃ Molecule

Bond Length	2.65 Å
Bond Angles	120 °
File Type	log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis Set	LANL2DZ
E(RB+HF-LYP)	-91.22
Gradient	0.00000090
Dipole Moment	0.00
Point Group	D3h

The link to the completed TlBr₃ optimisation file is: https://wiki.ch.ic.ac.uk/wiki/index.php?title=Image:TLBR3OPTIMISATION.LOG

The literature bond distance is 2.51 Å . This compares quite well with the computed bond distance with a difference of 2.65-2.51=0.14 Å. A greater accuracy could perhaps be obtained by using an even larger basis set however, the pseudo-potential assumption will always be a factor that reduced the accuracy of the results. The angle of 120° is the exact angle for a trigonal planar D_3h molecule.

A frequency analysis was then carried out to determine whether the optimisation had converged to a minimum or not. The same method and basis set must be used in order for the vibrational analysis to work. The frequency analysis needs to use an optimised structure according to the parameters and approximation of the basis set and method it uses itself. By computing frequencies of the molecule, a second derivative is being taken of the energy versus displacement optimisation graph in order to determine whether the critical point obtained by the optimisation is a maximum or a minimum. The critical point is defined as the point when the gradient is closest to zero and whether the critical point is a maxima or a minima depends on the sign of the frequencies. Positive frequencies indicate a minimum was reached, negative frequencies indicate a minimum was not reached.

Number	Form of the Vibration	Frequency	Intensity
1		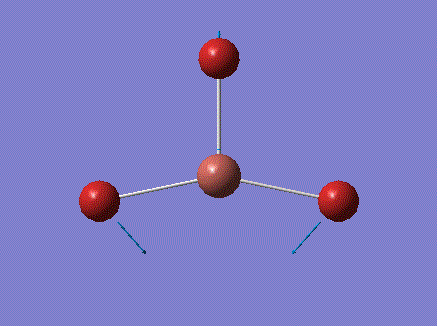46	4
2		46	4
3		52	6
4		165	0
5		211	25
6		211	25

All the frequencies shown above are positive which indicated that the critical point is a minimum. However, the log file must be examined in order to look at the "low" frequencies of TlBr₃.

Low frequencies:  -3.4213   -0.0026   -0.0004    0.0015    3.9367    3.9367

Although some of the low frequencies are negative, they are all within an error margin of 10 cm^-1 so it can be concluded that the molecule has indeed been optimised and the geometry obtained is a minimum on the potential energy surface. The lowest "real" normal mode is the doubly degenerate vibrations at 46 cm^-1.

In some structures, for example the initial optimised structures of the molybdenum complexes below, Gaussview does not draw a bond as if it were not there. This does not mean the bond has ceased to exist, Gaussview has a specific distance at which it considers there to be a bond between two atoms. This distance is dependent on the size and type of each atom. If the distance exceeds the expected bond distance in Gaussview's compiled list of typical bond distances, Gaussview no longer recognises the interaction between the two atoms as a bond, although it is still there.

What is a bond?

A chemical bond is a sharing of valence electrons between two atoms two form a stable compound. There are many different types of bonding or various degrees of strength. Electrostatic interaction is the attractive force that forms a bond between oppositely charged ions. Covalent bonds involve matching atomic orbitals of the same symmetry to form a new bonding orbital (in phase) and an antibonding orbital (out of phase). Hydrogen bonds are based only on weak interactions between electronegative atoms such as oxygen and fluorine and protons. Hydrogen bonds are not usually considered to be actual bonds and more intermolecular interactions. The inherent stability of a bond is due to the destabilising repulsion between the two atoms' positively charged nuclei being screened the most if the majority of electron density is situated between the two atoms. This is a very brief overview of bonding. There are many more types of bonding of various complexity such as 3-electron 2-centre bonds in diborane molecules through to dispersion forces. In short, bonds may be represented by lines between atoms but this is a gross oversimplification that doesn't take into account molecular orbitals at all. It is nonetheless a very useful technique.

Isomers of Mo(CO)₄L₂

The relative thermal stability and spectral characteristics were calculated for the cis and trans isomers of Mo(CO)₄(PPh₃)₂. In order to save computational time and resources, the bulky PPh₃ groups were approximated by PCl₃ groups. Chlorine atoms have been shown to have a similar electronic contributions to the bonding as the more computationally demanding phenyl groups.

The structures were drawn and then optimised in three steps. The first optimisation was carried out with a low level basis set and pseudo-potential, namely LANL2MB with a loose convergence criteria in order to get the geometry roughly correct. The calculation summary and geometry is found below:

First Optimisation Results

	Cis isomer DOI:10042/to-6604	Trans isomer DOI:10042/to-6603
Bond Length Mo-P	2.53 Å	2.48 Å
File Type	fch	fch
Calculation Type	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP
Basis Set	LANL2MB	LANL2MB
E(RB+HF-LYP)	-617.53	-617.52
Gradient	0.00001765	0.00003639
Dipole Moment	0.00	8.63

Reasonably good bond lengths and angles were obtained in this manner, however, the dihedral angles were not well-described. The optimised structures were therefore altered in order to set the torsion angles of the PCl₃ to the best start point before minimisation. For the trans-Mo complex, the best starting conformer is that with the PCl₃ groups eclipsed and with one Cl lying parallel to one Mo-C bond. For the cis conformer the best starting point is a structure with one Cl pointing up parallel to the axial bond and one Cl of the other group pointing down. The new geometries were then optimised still with the B3LYP method but this time with a better basis set and pseudo-potential, namely LANL2-DZ. The calculation summary and geometric analysis is shown below:

	Cis isomer DOI:10042/to-6605	Trans isomer DOI:10042/to-6606
Bond Length	2.51 Å	2.44 Å
File Type	fch	fch
Calculation Type	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP
Basis Set	LANL2DZ	LANL2DZ
E(RB+HF-LYP)	-623.58	-623.58
Gradient	0.00004623	0.00002996
Dipole Moment	1.3075	0.3051

The Final Optimised Structures of the Conformers

Trans isomer	Cis isomer
Lowest conformation structure	Lowest conformation structure

IR Analysis

IR Spectrum for cis Molybdenum complex

IR Spectrum for trans Molybdenum complex

Cis Molydenum Complex Predicted Vibrational dataDOI:10042/to-6623

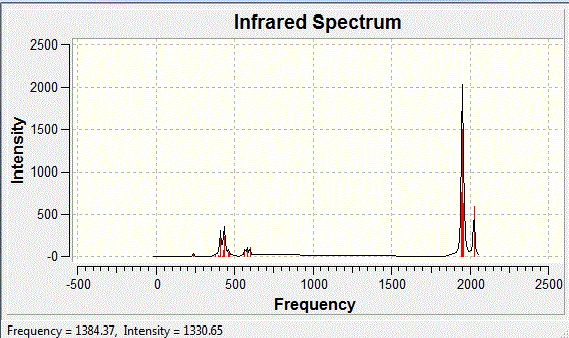
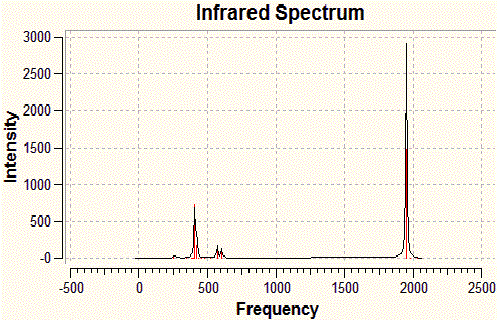
Frequency	Infrared	Form of Vibration
2024	597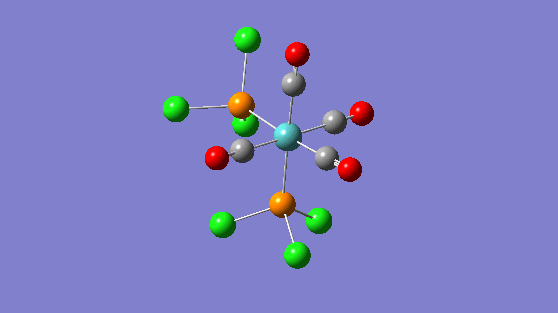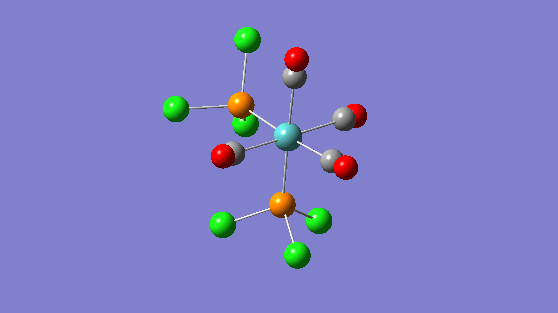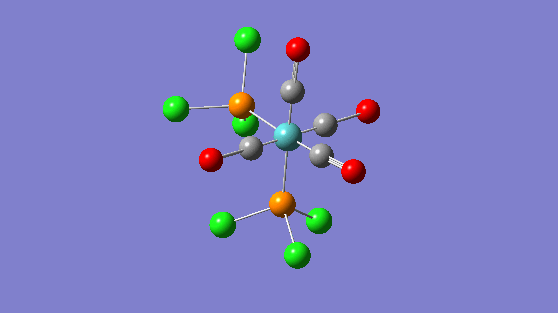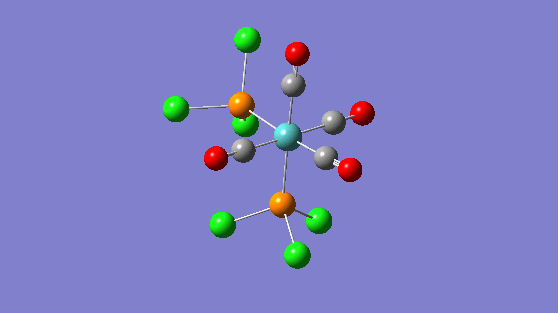
1959	634
1949	1450
1945	762

Trans Molydenum Complex Predicted Vibrational dataDOI:10042/to-6642

Frequency	Infrared	Form of Vibration
1951	1467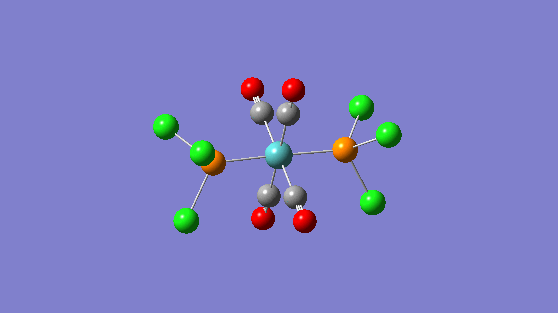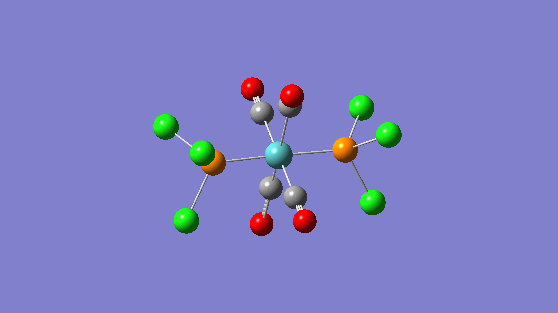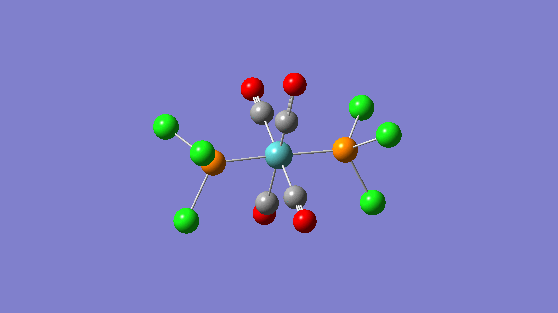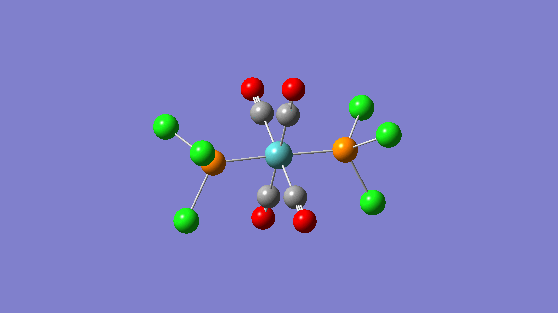
1950	1475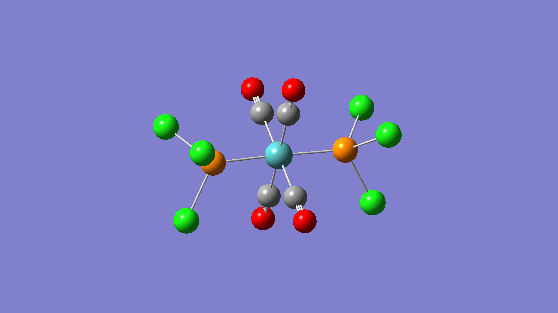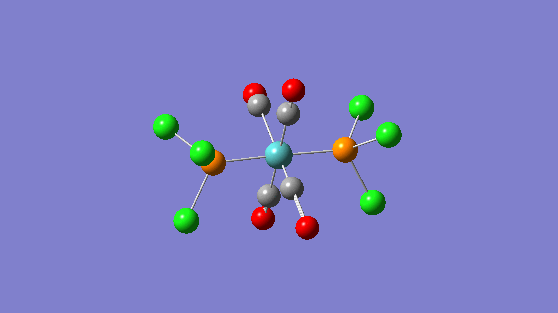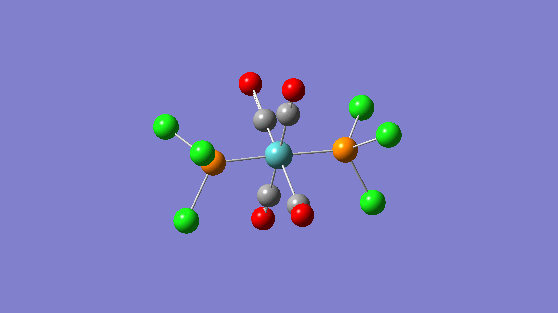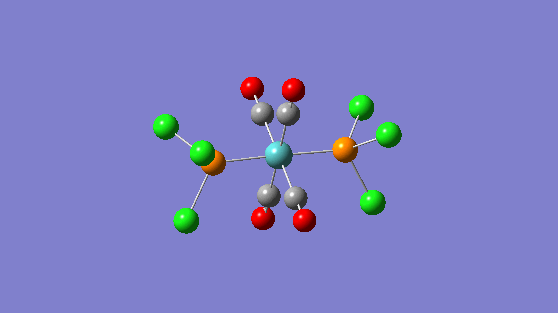

Conclusions

The cis Mo-P bond length was 2.51 Å and that of the trans was 2.44 Å. These are both relatively close to the literature bond length of 2.44 Å but evidently the trans isomer is an exact match. This is in fact quite surprising as the literature Mo-P bond length is not in the same complex but in a similar one, Mo(CO)₅P(OH)₃. The cis bond length is longer than the trans, this can perhaps be attributed to the steric bulk of the PCl₃ groups causing them to be pushed away from each other.

From comparison of the relative energies of the two isomers we can predict which conformer is the more stable of the two. However, the energies of the two isomers according to the calculation are almost exactly the same. The cis isomer has energy =-617.52510206 The trans isomer has energy=-617.52204755

It can also be seen that the energies of the molecules are very close although the cis isomer is very slight lower in energy. The difference between the structures is far smaller than the error on the calculations however. There are two effect that compete to dominate the stereochemistry of the complex. The first effect is steric repuslion which disfavours the cis isomer as this geometry has bulky PCl₃ groups adjacent to one another. The second effect is known as the thermodynamic trans effect whereby pi-acceptor ligands such as CO are more stable trans to a pi-donor ligands such as PR₃ as oppose to trans to other pi-accepting ligand which will compete for electron density on the metal. This trans effect of course favours the cis and disfavours the trans ligand. The outcome of these competing effects is determined by the extent to the steric repulsion caused by the PR₃ groups, i.e. the size of the R groups. In this case, the Chlorine atoms are an intermediate size so that sterics are not the overriding effect but note that the actual structure of the complex investigated had PPh₃ groups that were approximated by PCl₃ groups therefore, as phenyl rings are more bulky than chlorine atoms, this computation cannot be deemed accurate enough to determine which isomer is the most stable.

Mini project

For this mini-project, the geometry of the complex NiCl₂(PPh₃)₂ was analysed. This computational investigation is based on a first year inorganic experiment in which a NiCl₂(PPh₃)₂ was synthesised from NiCl₂.6H₂O and PPh₃ in the presence of ethanol and analysed using IR and UV spectroscopy. The colour of the complex was also indicative of whether the geometry was tetrahedral or square planar, in this case, the product obtained was a dark green colour. This cannot be analysed directly using computational methods but the size of the HOMO-LUMO gap can be analysed and used to predict what colour the complex should be.

Optimisation

The cis and trans isomers of the square planar and tetrahedral nickel complexes were optimised in an analogous way to the molybdenum complexes. They were each optimised in three steps in order to find out which has the lowest relative energy. The first optimisation used the B3LYP method; a low level basis set and pseudo-potential, namely LANL2MB with loose convergence criteria to get the rough geometry right. Next, the optimised LANL2MB structures were altered by changing the torsion angle of the PCl₃ groups before the second optimisation again using the B3LYP method but this time with the LANL2DZ pseudo-potential and basis sets; normal optimisation criteria and increased electronic convergence "int=ultrafine scf=conver=9". For the cis conformer, one Cl is orientated so that it points above the plane perpendicular to one Ni-Cl bond and one Cl of the other group points below the plane perpendicular to the other Ni-Cl bond. The trans conformer was changed so that both the PCl₃ groups are eclipsed and one Cl of each group lies perpendicular to the Ni-Cl bonds. Although, when the trans square planar complex is optimised it in fact optimises to a geometry with the PCl₃ staggered and the cis square planar complex distorts to an almost tetrahedral geometry.

First Optimisation Results

	Cis isomer DOI:10042/to-7066	Trans isomer DOI:10042/to-7064	Tetrahedral Isomer DOI:10042/to-7067
Bond Length Ni-P	2.62 Å	2.44 Å	2.49 Å
Bond Length Ni-Cl	2.22 Å	2.25 Å	2.32 Å
File Type	fch	fch	fch
Calculation Type	FOPT	FOPT	FOPT
Calculation Method	R3LYP	RB3LYP	RB3LYP
Basis Set	LANL2MB	LANL2MB	LANL2MB
E(RB+HF-LYP)	-301.73	-301.79	-301.79
Gradient	O.OOOO0786	0.00002537	0.00003580
Dipole Moment	2.4546	2.6076	0.0002

Second Optimisation Results

	Tetrahedral isomer DOI:10042/to-7067	Cis isomer DOI:10042/to-7071	Trans isomer DOI:10042/to-7072
Bond Length Ni-P	2.31 Å	2.43 Å	2.34 Å
Bond Length Ni-Cl	2.25 Å	2.18 Å	2.20 Å
File Type	fch	fch	fch
Calculation Type	FOPT	FOPT	FOPT
Calculation Method	RB3LYP	RB3LYP	RB3LYP
Basis Set	LANL2MB	LANL2MB	LANL2MB
E(RB+HF-LYP)	-301.92	-301.94	-301.96
Gradient	0.00000791	0.00000168	0.00000173
Dipole Moment	3.8512	3.3924	0.0004

The Final Optimised Structures of the Conformers

Tetrahedral isomer	Trans square-planar isomer	Cis square-planar isomer
Lowest conformation structure	Lowest conformation structure	Lowest conformation structure

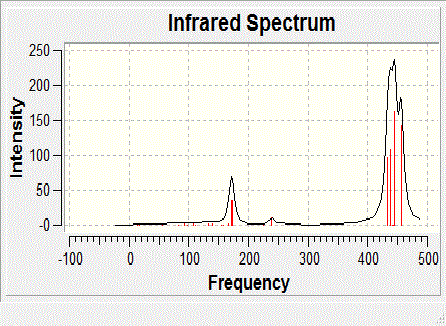
Frequency Analysis

The three conformers were then analysed using the same method and pseudo-potential as the optimisation (B3LYP, LANL2DZ, etc.) in order to determine whether the structures obtained were in actual fact the minimum conformer of the optimisation. The results are shown in the table below:

IR spectrum of cis square planar structure

Cis-square planar Ni complex

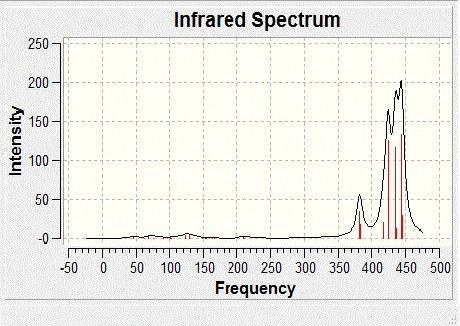
Frequency cm-1	Infared	Form of vibration
381	35
424	116
435	116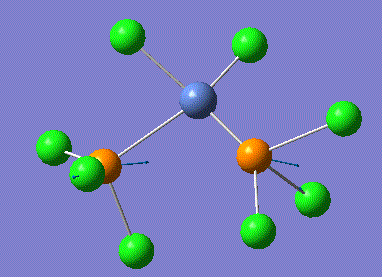
443	133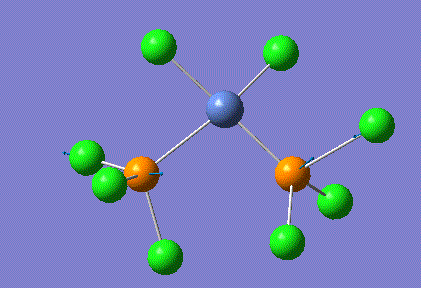

IR spectrum of trans square planar structure

Cis-square planar Ni complex

Frequency cm-1	Infared	Form of vibration
173	36
433	97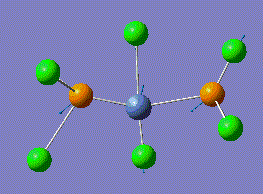
437	110
445	162
456	143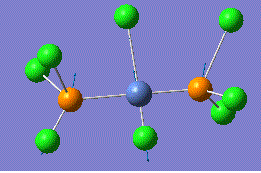

IR spectrum of tetrahedral structure

Cis-square planar Ni complex

Frequency cm-1	Infared	Form of vibration
423	49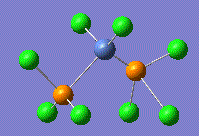
430	130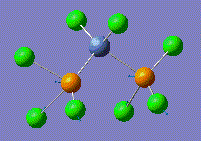
441	154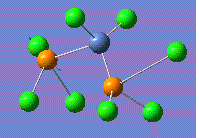
442	153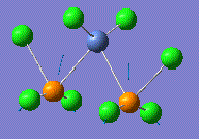

Conclusions

In conclusion, the outcome of this computational experiment is not what was to be expected. In terms of the optimisation, the most theromdynamically stable geometric isomer of NiCl₂(PPh₃)₂ is the trans square planar isomer followed by the cis square planar isomer followed by the tetrahedral isomer. The experimental outcome is that the tetrahedral isomer is the most stable although the isomerisation energy between square planar and tetrahedral structures is small so at elevated temperatures an equilibrium of the two may exist.. This may in fact be due to the approximation of the PPh₃ by PCl₃: the chlorine atoms are not as bulky as the phenyl rings which may mean that steric effects are not as dominant as they might be with the exact molecule. It is expected that the trans square planar isomer will be more stable than the cis isomer as there are no trans effects as with the molybdenum isomers so the steric effect of having two adjacent phosphine ligands is dominant and thus disfavours the cis isomer, although not by much. All in all the energies are very very close so the margin of error disregards the results. The vibrational frequencies of the tetrahedral isomer match those obtained in the experiment which suggests that it was indeed the tetrahedral isomer that was formed.