Rep:Mod:hampluscheese

Module 3:Physical Computational Chemistry Lab

Objectives

The aim of this experiment is to is to use various levels of theory (HF/3-21G, DFT/B3LYP/6-31G (d) and AM1/semi-empirical) on Gaussian to calculate various energies, molecular orbitals, geometrical parameters, reaction coordinate pathways and low and imaginary frequencies for a range of molecules and transition states. This will include using different optimisation methods throughout and will lead to a range of findings in various areas of chemical interest.

The Cope Rearrangement

The Cope rearrangement is a |3,3|-sigmatropic rearrangement that takes place through a single pericyclic, concerted transition state. Within this rearrangement a σ bond is formed in concert with another being broken within a conjugated π system.

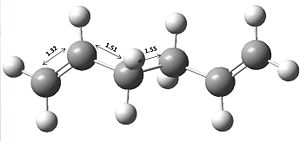
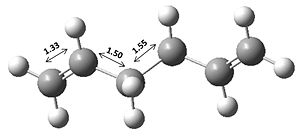
The Cope rearrangement we will be studying will be that of 1,5-hexadiene, which is shown below.

The objective is to locate the low-energy minima and transition structures on the C₆H₁₀ potential energy surface and to determine the preferred reaction mechanism by using Gaussian, with the Hartree-Fock (HF) and density functional theory (DFT) methods.

Optimisation of 1,5-hexadiene Conformers

Rough and conformers of 1,5-hexadiene were drawn on Gaussview and their structures were tidied by the clean function. They were then further optimised by the HF/3-21G method and were identified which conformer they were from their point group and appendix 1 on the physical lab page.

Table 1: Optimisation and comparison of anti and gauche 1,5-hexadiene conformers using HF/3-21G methods

Conformer	Optimised Structure	Energy (Atomic Units)	Appendix 1 Energies (Atomic Units)	Energy (KJ mol-1)	ΔE (Anti2 - Gauche3)	Point group
Anti2		-231.692535	-231.69254	-6.08 x 105	1.2606 x 10-4 a. u	Ci
Gauche3		-231.692661	-231.69266	-6.08 x 105	3.31 x 10-1 KJ mol-1	C1

From studying table 1 it can be seen that the gauche conformer is 0.33 KJ mol^-1 more stable than the anti conformation. One would assume that the anti2 conformer would be more stable due to steric factors/repulsion within the gauche3 conformation. However within the gauche3 conformer there is a favourable donation of electron density from the C=C π orbital to the C-H σ* orbital from the adjacent proton, which stabilises the conformer.

The anti2 conformer was then optimised using the DFT/B3LYP/6-31G* (6-31G (d)) method.

Table 2: Comparison of the anti2 conformer optimisations carried out at different calculation methods

Method	Structure and bond distances (Å)	Dihedral angle (C1 to C4)	Energy (Atomic Units)]	Energy (KJ mol-1)	ΔE (HF/3-21G - DFT/B3LYP/6-31G*)
HF/3-21G		114.6 o	-231.692535	-6.08 x 105	2.919171 a. u
DFT/B3LYP/6-31G*		118.8 o	-234.611716	-6.16 x 105	7.66 x 103 KJ mol-1

From examining table 2 at first it is possible to see that the bond lengths are very similar to each other and that of the literature bond lengths (C₁=C₂: 1.340 Å, C₂-C₃: 1.508 Å and C₃-C₄: 1.538 Å). It is also possible to see that the C=C bond length is more accurate for the DFT/B3LYP/6-31G* method by it being 0.01 Å closer to the literature value. Another main difference in terms of geometry is that the DFT/B3LYP/6-31G* method gives a larger dihedral angle (and most likely more accurate) of 118.8^o compared to that of 114.6^o.

In terms of energy the DFT/B3LYP/6-31G* method produces a conformer of a higher stability by it possessing a lower energy with a difference of 7.66 x 10³ KJ mol^-1.

Frequency analysis of 1,5-hexadiene Conformers

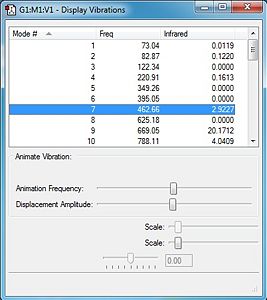
For the frequency analysis the DFT/B3LYP/6-31G* method was used.

Frequency analysis is essential within this calculation due to it being the second derivative of the potential energy surface. This means that if all the frequencies are all positive the system is at a minimum, if one of them is negative the optimised system is at a transition state, and if more than one are negative then the calculation has failed to find a critical point, which means the optimisation has failed. This therefore gives us a method of seeing whether the calculation has worked.

From looking to the image on the right it can deduced that the optimisation has taken place successfully by there being no negative vibrations and therefore the conformation is at a minimum.

Table 3: Energies under the thermochemistry section at 298.15 K and 0 K within the frequency logfiles

Energies	298.15 K (atomic units)	0 K (atomic units)	ΔE, 298.15 K - 0 K (atomic units)	ΔE, 298.15 K - 0 K (KJ mol-1)	Discussion
Sum of electronic and zero-point energies	-234.469177	-234.466673	-2.504 x 10-3	-6.57	This is the potential energy at 0 K, which includes the zero-point vibrational energy (E = Eelec + ZPE).
Sum of electronic and thermal energies	-234.461835	-234.461085	-7.5 x 10-4	-1.97	This is the energy at 298.15 K (0 K for 0 K calculation) and 1 atm of pressure, which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + Evib + Erot + Etrans).
Sum of electronic and thermal enthalpies	-234.460891	-234.460141	-7.5 x 10-4	-1.97	This contains an additional correction for RT (H = E + RT), which is especially important when looking at dissociation reactions.
Sum of electronic and thermal free energies	-234.500739	-234.495931	4.808 x 10-3	-12.62	This includes the entropic contribution to the free energy (G = H - TS).

IR spectrum of the anti2 conformer at 298.15 K

IR spectrum of the anti2 conformer at 0 K

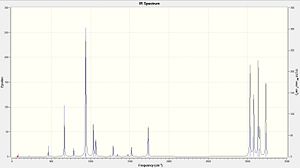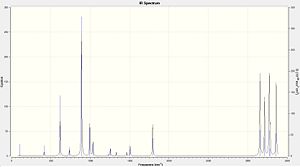From looking at table 3 above it can be deduced that the anti2 conformer is more stable at room temperature to that of 0 K with respect to all the types of energies. The spectra also seem to not change much between the two temperatures but the main change is the change in the sum of electronic and thermal free energies, which is heavily dependent of temperature by it including the entropic contribution to the free energy (G = H - TS).

Optimizing the "Chair" and "Boat" Transition Structures

Within the Cope Rearrangement there are two possible transition states, the chair (C_2h) and the boat (C_2v), which are shown within appendix two .

Comparison of optimisation methods for the chair transition state

An , CH₂CHCH₂ was drawn on Gaussview and was optimized through the HF/3-21G method. After this the original allyl fragment was copied and pasted into a new window and placed exactly above the first fragment with a bond distance of 2.20 Å between the terminal end carbons. This therefore produced the

Gaussian was then set up for an optimisation for the transition state with the additional key words "Opt=NoEigen", the optimisation set to TS (Berny), the force constants set to "once" and using the HF/3-21G method.

After this the "chair" transition state was optimised an alternative way by freezing the coordinates of the two sets of terminal carbons (where the bonds form/break during the rearrangement) within the Redundant Coord Editor on Gauusview. Following this a second calculation was run where the freeze coordinates option was changed to "Derivative" and the force constants were set to "never".

Table 4: Comparison of chair transition state optimisation methods

	Optimised through a TS (Berny)	Optimised through a frozen coordinate method
Optimised TS Structure
Terminal C-C bond length (Å)	2.02	2.02
Energy (atomic units)	-231.61932247	-231.61932190
ΔE, TS (Berny) - frozen coordinate	5.7 x 10-7 a.u	1.50 x 10-3 KJ mol-1
Imaginary frequency (cm-1)	-818	-818
Animation

The data in table 4 shows that both methods give the same results and they both give the same transition state. They both produced the same energy with a negligible energy difference between them and the bond lengths between the terminal carbons are both 2.02 Å. In addition to this the imaginary frequencies were both -818cm^-1 and within the animations above it is possible to see that when one C-C bond is forming the other is breaking. This means it is a asynchronous bond formation, which is expected for the Cope Rearrangement since it is a pericyclic reaction.

The only difference between the two optimisations is the way in which the transition states were calculated. This is due to the TS (Berny) method calculating the force constant matrix within the first optimisation step and is then being recalculated as the optimisation carries on. When the frozen coordinate method freezes the reaction coordinate in order for the rest of the structure to be optimised around it, which does not require the whole hessian (force constant matrix) to be calculated but only that the reaction coordinate is differentiated (second step). The main advantage of this, is that you do not need to calculate the entire force constant matrix and just need to differentiate the reaction coordinate in order to obtain a good enough guess for the initial force constant matrix. The frozen coordinate method will therefore take less time to compute the transition state, which can be very expensive within certain systems. However to carry out this method one needs to have an idea of how far apart the terminal carbons are.

Boat transition state

QST2 optimisation

The optimisation for the boat transition state had a different method and this was the QST2 method. This calculation interpolates between two structures (product and reactant) and tries to find a transition state between them.

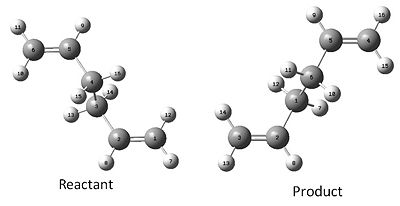
The reactants and products were numbered in the same way. Therefore both 1,5-hexadiene molecules had their numbering manually changed for the product molecule so it corresponded to the numbering of the reactant if it rearranged. This is illustrated in the reaction scheme below.

The chk file for the optimized anti2 conformer was opened and copied into a new window. A second window was opened within the new window and the same anti2 conformer was copied into the new window. The numbering was changed within the second molecule so the two looked like they do in the image below.

The job type was set as "Opt+Freq" and "TS (QST2)" was chosen to optimise the transition state. However this failed and produced a structure a bit like a but more dissociated. This is because it interpolated between the two structures and translated the top allyl fragment and therefore did not consider the possibility of a rotation around the central bonds.

To get around this the C-C-C-C dihedral angle (C₂-C₃-C₄-C₅) was set to 0 ^o and the C-C-C angle (C₂-C₃-C₄ and C₃-C₄-C₅ for the product molecule) was set to 100 ^o for both molecules. This gave rise to the two structures below.

After this the QST2 calculation was run again and the results in table 5 were produced. The imaginary frequency at -839 cm^-1 shows that while one bond is forming the other one is breaking, which is again an asynchronous bond formation. It is also possible to see that the boat transition state has a longer terminal C-C bond length by 0.12 Å to that of the chair.

Table 5: Data for the boat transition state from the QST2 optimisation method

Optimised TS Structure
Terminal C-C bond length (Å)	2.14
Energy (atomic units)	-231.603
Imaginary frequency/ cm-1	-840
Animation	[[Image:]]

Intrinsic Reaction Coordinate

It is not possible to predict which product the chair and boat transition state will lead to. To solve this problem within Gaussian one can use the IRC method, which allows one to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. This creates a succession of points by taking small geometry steps in the direction to where the gradient of the energy surface is at its steepest until the minimum in energy is reached.

The chk file for the optimized chair transition structure was opened and the job type selected was "IRC", the reaction coordinate was computed in the forward direction (since molecule is symmetric) with 50 points along the IRC. This was done with two type of force constants being calculated, once and always.

Within the "once" method the output showed no bond formation process by the 26th step and therefore the calculation was incomplete, since a complete 1,5-hexadiene structure was supposed to be formed. From looking at the IRC pathway it can be seen that the minimum on the potential energy surface was not reached at that point, since the points on the pathway did not form an asymptote and the gradient did not go close enough to zero.

For the "always" method the computation of force constants were carried out at every step. This therefore lets the IRC calculation distinguish whether it is moving along the minimum energy pathway while going down the potential energy surface. While this is happening it can make changes to the pathway if necessary. Within the "always" case the bond forming arrives at 1,5-hexadiene and this is backed up by the IRC pathway reaching a minimum within its energy by the gradient going close to zero and the pathway reaches an asymptote.

The structure produced through the always method had an energy of -231.69199434 atomic units, which is very close to the energy of the gauche2 conformer in the appendix 1. This suggests that the reaction takes place through the chair transition state, which later produces the gauche2 conformer of 1,5-hexadiene.

Table 6: Comparison of IRC calculations for the chair structure

	Calculate force constants once	Calculate force constants always
Number of points along IRC	26	47
Structure at the last point of IRC
Energy (atomic units)	-231.68906923	-231.69199434
ΔE, once - always	2.92511 x 10-3 a.u	7.68 KJ mol-1
IRC pathway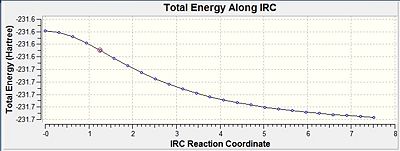
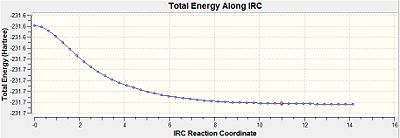
IRC gradient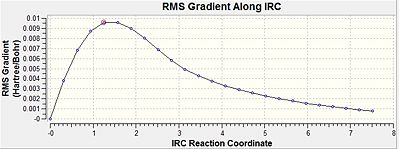

Comparison of activation energies for the transition states

The HF/3-21G optimised chair and boat transition structures were both reoptimised using the B3LYP/6-31G* (B3LYP/6-31G (d)) method. This gives a more accurate minimisation however this method takes longer to run. The values for the zero-point energies and thermal energies were found within the thermochemistry section of the log file.

The values for the HF/3-21G reactant (anti2) optimisation were calculated and the B3LYP/6-31G* values were taken from the "Frequency analysis of 1,5-hexadiene Conformers" earlier in this module.

Table 7: Energy data for chair, boat and the anti2 conformation from the HF/3-21G and B3LYP/6-31G* methods of optimisation

	HF/3-21G			B3LYP/6-31G*
	Electronic energy (a.u)	Sum of electronic and zero-point energies (a.u)	Sum of electronic and thermal energies (a.u)	Electronic energy (a.u)	Sum of electronic and zero-point energies (a.u)	Sum of electronic and thermal energies (a.u)
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466677	-231.461320	-234.556983	-234.414929	-234.409008
Boat TS	-231.602802	-231.450936	-231.445303	-234.543093	-234.402342	-234.396008
Reactant (anti2)	-231.692535	-231.539524	-231.532562	-234.611716	-234.469177	-234.461835

Digital repositories

Chair: HF/3-21G: http://hdl.handle.net/10042/to-5569 B3LYP/6-31G*: http://hdl.handle.net/10042/to-5568

Boat: HF/3-21G: http://hdl.handle.net/10042/to-5570 B3LYP/6-31G*: http://hdl.handle.net/10042/to-5571

Table 8: Summary of activation energies for the chair and boat conformations (ΔE = chair TS or boat TS minus anti2)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
1 a.u = 627.509 kcal mol-1	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE, chair (a.u)	0.072847	0.071242	0.054248	0.052827	-
ΔE, chair (kcal mol-1)	45.71	44.70	34.04	33.15	33.5 ± 0.5
ΔE, boat (a. u)	0.088588	0.087259	0.066835	0.065827	-
ΔE, boat (kcal mol-1)	55.59	54.76	41.94	41.31	44.7 ± 2.0

By examining table 8 it is clear to see that the B3LYP/6-31G* method gives values which are much closer to the experimental ones. This is due to the B3LYP/6-31G* giving a higher level of optimisation than the HF/3-21G method. Table 8 also shows that the chair transition state has a lower activation energy to that of the boat transition state by 8.16 kcal mol^-1. This suggests that the Cope rearrangement mechanism would most likely proceed through the chair transition state to that of the boat. Therefore the reaction would take place from the anti2 conformer to the chair transition state and then onto the gauche2 conformer within the Cope rearrangement.

It is also possible to see that the calculated energies are very close to the literature values with the chair conformation being closer to its literature value to that of the boat.

Table 9: Geometric parameters for the optimised chair and boat structures

	HF/3-21G chair TS	B3LYP/6-31G* chair TS	HF/3-21G boat TS	B3LYP/6-31G* boat TS
Optimised Structure
Terminal C-C bond length (Å)	2.02 (C5-C10 or C3-C14)	1.97 (C5-C10 or C3-C14)	2.14 (C3-C4 or C1-C6)	2.21 (C3-C4 or C1-C6)
Fragment angle	120 o (C3-C1-C5)	120 o (C3-C1-C5)	122 o (C4-C5-C6)	122 o (C4-C5-C6)
Dihedral angle	55 o (C1-C3-C14-C11)	54 o (C1-C3-C14-C11)	0 o (C2-C1-C6-C5)	0 o (C2-C1-C6-C5)
Numbering of carbons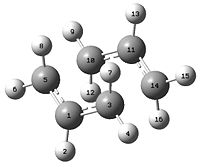

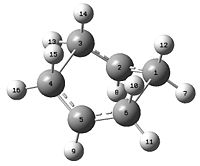From studying table 9 it can be seen that the C-C bond breaking/forming length has changed between the two different types of optimisation methods. However the angles between the bonds remains unchanged.

The Diels Alder Cycloaddition

The Diels-Alder reaction is a cycloaddition between a conjugated diene and a dienophile (alkene system), which forms a cyclohexene system. It is often referred to as a [4s+2s] cycloaddition and proceeds through a single cyclic, concerted transition state where 2 σ bonds are formed in between the terminal carbons of the 2 п systems. This is shown in the reaction scheme below where ethene is reacting with cis-butadiene.

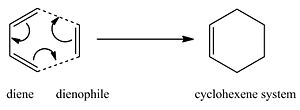
The π orbitals of the dienophile form new σ bonds with the π orbitals of the diene. The number of π electrons involved determine whether the reaction proceeds in a concerted stereospecific fashion (allowed) or not (forbidden). The HOMO/LUMO of one fragment interacts with the HOMO/LUMO of the other fragment to form two new bonding and anti-bonding MOs. The nodal properties allow one to predict how the reaction will occur.

Semi-Empirical/AM1 method and the B3LYP/6-31G* method of optimisation will be used on Gaussian to determine particular properties of the reactants to predict the way in which the reaction will proceed.

cis-butadiene and ethylene: reagents

and were optimised separately using the AM1 semi-empirical method on Gaussview.The cis-butadiene had an energy of 0.04879725 a. u (1.28 x 10² KJ mol^-1) and ethylene had an energy of 0.02619027 a. u (68.76 KJ mol^-1).

Table 10: Frontier molecular orbitals of cis-butadiene and ethylene

Reagent	Molecular Orbital	View 1	View 2	Symmetry with respect to the plane	Energy (a. u)
cis-butadiene	LUMO			Symmetric	+0.017
cis-butadiene	HOMO			Anti-symmetric	-0.343
ethylene	LUMO		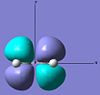	Anti-symmetric	+0.052
ethylene	HOMO		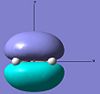	Symmetric	-0.387

The symmetries of the LUMO and HOMO orbitals for cis-butadiene are opposite of those for the ethylene. This therefore means that the only interactions that can take place are those between ethylene's LUMO and cis-butadiene's HOMO and in addition to this the interaction between cis-butadiene's LUMO and ethylene's HOMO. This is because orbital symmetry has to be conserved (the conservation of orbital symmetry states that the symmetry of an new orbital formed by the overlap of the 2 original orbitals must be the same as the symmetry of the initial orbitals).

cis-butadiene and ethylene: transition state

A was drawn and one of the -CH2-CH2- fragments were removed. Three C=C bonds were added and the previous one was taken away so a was produced.

After this an optimisation and frequency (Opt+Freq) calculation was run to a minimum using the semi-empirical/AM1 method while bonds between the termini of the fragments were frozen at 2.1Å. Following this the resulting file had two separate optimisation and frequency calculations run on it using the TS (Berny) with one using the semi-empirical/AM1 method and the other using the DFT/B3LYP/6-31G* level of theory. Both of these optimisations had the bonds unfrozen and the "derivative" option was chosen instead.

The DFT/B3LYP/6-31G* level of theory was used since it gave more accurate results in the calculations before and the energies it produces are consistent with the rest of the report (semi-empirical/AM1 method gives very different values).

The QST2 optimisation was not used since it required numbering the atoms, which would of taken a lot of time.

Table 11: Comparison of two methods of optimsations for the transition state

	semi-empirical/AM1 method	DFT/B3LYP/6-31G* method
Structure
Energy (a. u)	0.11165608	-234.54389573
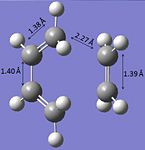
Bond lengths
Imaginary frequency (cm-1)	-957	-525
Animation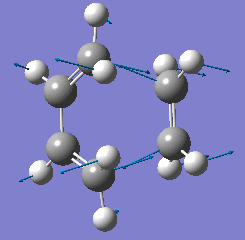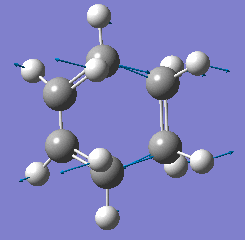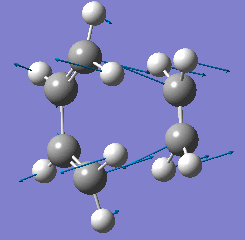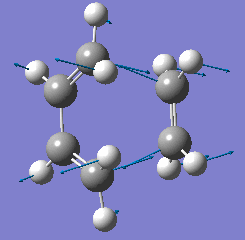
Lowest real frequency (cm-1)	148	136
Animation

The C-C bond forming length between the terminal carbons is 0.15 Å larger for the DFT/B3LYP/6-31G* level of theory and this is because this method gives carries out the calculation to a greater degree of accuracy. This larger bond length leads a lower potential energy gradient to the transition state, which gives a lower total energy for the transition state. Therefore the given values below will be from the DFT/B3LYP/6-31G* and not the semi-empirical/AM1 method.

A typical sp3 C-C bond length is 1.54 Å and a typical sp2 C=C bond length is 1.34 Å. Within the optimised transition molecule above the C-C bond lengths are 1.40 Å and the C=C bond length is 1.38 Å. This suggests that the π-bonds are breaking in order for the C-C bonds to form and additionally to this a π-bond is forming in between the two sp3 carbons.

The Van der Waals radius of a C-atom is 1.72 Å. The partly formed C-C length is 2.27 Å, which is shorter than two times the the van der Waals radius of a carbon atom. Therefore the carbon atoms are within a close enough distance to each other to share electron density.

From looking at the animations for the imaginary frequency above it can be seen that the formation of the two bonds between the termini of the reactants is synchronous. This is expected of the Diels-Alder reaction since the mechanism is concerted. However the lowest real frequency is asynchronous with respect to the two bonds forming between the termini.

Table 12: Frontier molecular orbitals of the transition state

Molecular Orbital	View 1	View 2	Symmetry with respect to the plane	Energy (a. u)
LUMO			Symmetric	+0.023
HOMO			Anti-symmetric	-0.323

From examining the images from table 12 above it can be deduced that the LUMO of the transition state originates from the cis-butadiene's LUMO and the ethylene's HOMO, which represents the σ*-antibonding orbitals. However the HOMO of the transition state originates from the cis-butadiene's HOMO and the ethylene's LUMO, which represents the σ-bonding orbitals within the two single C-C bonds that are formed within the reaction.

cis-butadiene and ethylene: activation energy

The cis-butadiene and ethylene were re-optimised at the DFT/B3LYP/6-31G* level of theory so the activation energy of the reaction could be calculated.

Table 13: Calculation for the activation energy for the reaction

molecule	DFT/B3LYP/6-31G* energy (a. u)	Calculations	Energy
cis-butadiene	-155.98595591	transition state	-234.54389573 a. u
ethylene	-78.58745828	ΔE, activation energy	0.02951846 a. u
cis-butadiene and ethylene combined	-234.57341419	ΔE, activation energy	77.50 KJ mol-1

The calculated activation energy is 77.50 KJ mol^-1, which is of the right magnitude when compared to the literature value (115 ± 8 KJ mol^-1 at 0 K) but there is still an error of 37.50 KJ mol^-1. This shows that Gaussview is not perfect but still gives an idea of the activation energy required for the reaction to take place.

Cyclohexa-1,3-diene reaction with maleic anhydride

The reaction scheme below shows the stereoselective Diels-Alder cycloaddition of maleic anhydride with cyclohexa-1,3-diene. The reaction is kinetically controlled with the major product being the endo product, which will be explained later on in the exercise.

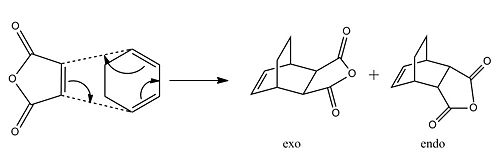
The and transition states were drawn on Gaussview and then the optimisation and frequency (Opt+Freq) calculation was run to a minimum using the semi-empirical/AM1 method while the distance of the forming bonds were frozen at 2.1Å between the respective carbons. After this the structures changed slightly ( and ) and the resulting files had an optimisation and frequency calculation run on it using the TA (Berny) with using the semi-empirical/AM1 level of theory while the unfrozen option as changed to "derivative". After this the endo and exo optimised transition state structures were re-optimised as they were before but using the DFT/B3LYP/6-31G* level of theory instead with the additional keyword "Opt=NoEigen".

Table 14: Comparison of the exo and endo transition states

-	exo		endo
	Semi-empirical/AM1	DFT/B3LYP/6-31G*	Semi-empirical/AM1	DFT/B3LYP/6-31G*
Structure
Energy (a. u)	-0.05041975	-612.67931095	-0.05150470	-612.68339684
C-C bond forming length (Å)	2.17	2.29	2.16	2.27
Imaginary frequency (cm-1)	-812	-448	-806	-447
Animation

Again the C-C bond forming length between the termini carbons is larger (by 0.11 and 0.12 Å) for the DFT/B3LYP/6-31G* level of theory and this is due the same reasons talked about above. However the C-C bond forming length between the termini carbons are very similar in both the endo and exo transition states (0.02 Å difference).

From looking at the animations for the imaginary frequency above it can also be seen that the formation of the two bonds between the carbons in this case as well is synchronous. Again this is expected of the Diels-Alder reaction since it is concerted.

Strain diagrams for the endo and exo transition states

Exo TS

Endo TS

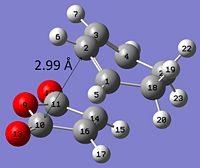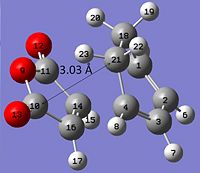
From studying the energies in table 14 it can be seen that the endo transition state is more stable than the exo by 4.08589 x 10^-3 a. u (10.73 KJ mol^-1). However by looking at the strain of both transition states one would expect the exo TS to be more stable. This is because the distance between the cyclohexa-1,3-diene ring and the -(C=O)-O-(C=O)- maleic anhydride fragment is 2.99 Å in the endo TS and 3.03 Å in the exo TS. Thus the endo form would have more strain due to steric hindrance.

However within the exo TS the vicinal hydrogens on the CH₂-CH₂ (carbon numbers 18 and 21) fragment on the cyclohexa-1,3-diene ring are found below the plane and next to the maleic anhydride. This leads to steric hindrance is this is where the strain originates from within the exo TS. Therefore this disfavours the exo form, which makes the endo more stable.

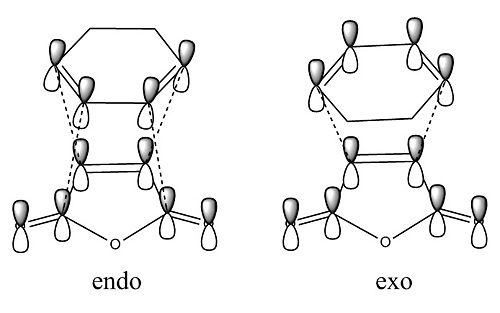
Another factor making the endo TS more favourable is secondary orbital overlap. These orbitals contribute to the bonds forming and they interact with each other through space. Within the endo TS below there are 2 more orbitals interacting (secondary orbitals) than within the exo TS. This therefore makes the endo TS more stable and therefore more favoured.

Table 15: Frontier molecular orbitals of the the transition state for the cyclohexa-1,3-diene reaction

Molecular Orbital	exo				endo
	View 1	View 2	Symmetry with respect to plane	Energy (a. u)	View 1	View 2	Symmetry with respect to plane	Energy (a. u)
LUMO		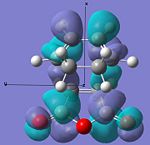	Anti-symmetric	-0.078		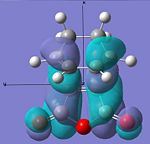	Anti-symmetric	-0.067
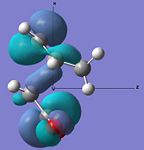
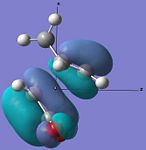
HOMO		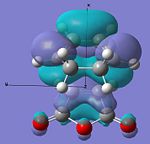	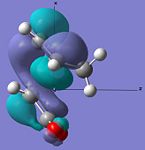Anti-symmetric	-0.242		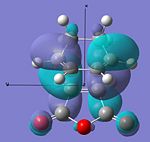	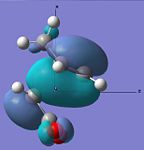Anti-symmetric	-0.242

Digital repositories:

exo: http://hdl.handle.net/10042/to-5596

endo: http://hdl.handle.net/10042/to-5597

From examining table 15 it is clear to see that both the HOMO and LUMO are anti-symmetric for both the transition states. The LUMO of the maleic anhydride fragment is the π* anti-bonding orbital of the C=C bond. Within the reaction then this has electrons transferred to it and the C=C bond breaks, which leaves just a C-C bond. The LUMOs for both transition states are both anti-bonding with respect to the two fragments. The HOMOs of both transitions state represent the σ-bonding that will be formed between the termini carbons on the products and reactants. This is most likely from the overlap of the cyclohexa-1,3-diene's HOMO and the maleic anhydride's LUMO.