Rep:Mod:ha3915mgo

Thermal expansion of MgO

Abstract

The thermal expansion coefficient of a face-centered-cubic (fcc) MgO lattice, $\alpha$, was computed using two techniques, the quasi-harmonic approximation and through a molecular dynamics simulation to predict its thermal behaviour. The linear expansion coefficient was computed to be 10.6e-6 K^-1 and 10.5e-6 K^-1 using the quasi-harmonic approximation and the molecular dynamics simulation respectively.

Introduction

A simple model of atomic interactions was used to calculate the energy and vibrations of an MgO crystal - which was used to calculate the Helmholtz free energy of the system. This was taken further by then looking at the molecular dynamics of the crysthus reproducing the vibrations of the atoms and comparing both methods.

• The thermal expansion coefficient of MgO was determined, this allowed the prediction of the expansion behaviour of the material when heated. The thermal expansion coefficient is given by:

$\alpha =\frac{1}{V_0}{\left(\frac{\partial V}{\partial T}\right)}_p$

• The vibrational energy levels of MgO were computed using the quasi-harmonic approximation and phonon dispersion and vibrational density of state was discussed.
• Molecular dynamics simulations were used for the and compared with the quasi-harmonic approximation results.

The face-centered cubic crystal structure of MgO was the system used to perform the calculations and simulations. a 3D modelled representation of the conventional unit cell is shown below.

Figure 1: Conventional 3D representation of MgO crystal

It should be noted that this is the conventional unit cell, consisting of 8 atoms, where as the primitive unit cell consists of only 2 atoms: 1 Mg and 1 O, as such $V_C=4V_P$. The primitive cell is the smallest repeatable unit of the structure.

Considering atomic vibrations in 1-dimension, where a is the atomic separation, the wavelength, $\lambda$, is defined as the set of periodic vibrating units. This is in turn defined by the phase separation between each vibration between each atom.

We define a wavevector, $k$, where

$k=\frac{2\pi }{\lambda }$

such that as k increases, the energy of vibration increases as well as the frequency. Assuming a spring-like vibration, using Hooke's law, it can be predicted that the vibrational frequency, ${\omega }_k$is given by:

${\omega }_k=\sqrt{\frac{4J}{M}}|sin(\frac{ka}{2})|$

where $J$ is the force constant of the "spring" between atoms, $M$ is the reduced mass of two atoms and $a$ is the lattice parameter.

In this system, since it's fcc, only one lattice parameter is required to fully describe the dimensions of the crystal as $a=b=c$where a b and c are lattice parameters in 3D.

We define the lattice parameter in reciprocal space as $a^{*}=\frac{2\pi }{a}$

In an infinite lattice, there are many vibrational states, such that a continuum of states, called bands, are formed.

A grid of k-points can be used to sample the free energy in the reciprocal space. The shrinking factor is the number of sampling points used in each dimension. The more k-points used, the more accurate the simulation. When treating vibrations as particles, similarly to photons with radiation, the "energy packets" are called phonons. The phonon dispersion curves are shown later down the page.

Since we are considering the change in volume with temperature, it was decided that the Helmholtz free energy would be most suited as $F=F(T,V)$, where $F$ is the Helmholtz free energy.

In the quasi-harmonic approximation, the free energy can be calculated by:

$F=E_0+\frac{1}{2}\sum _{k,j}\hslash {\omega }_{j,k}+k_{B}T\sum _{k,j}ln[1-exp(\frac{-\hslash {\omega }_{j,k}}{k_{B}T})]$

where $E_0$ is the initial internal energy, $\frac{1}{2}\sum _{k,j}\hslash {\omega }_{j,k}$ is the zero-point energy of vibrations where $j$ is the number of branches, the third term is the entropic contribution.

This was achieved using the General Utility Lattice Program, GULP with DLVisualize - a general purpose GUI for modelling on the RedHat Linux distribution - an open source operating system environment.

Initial Calculation - Internal energy of MgO crystal

A single point Buckingham potential calculation was performed as a starting point. The buckingham potential empirically describes the repulsive potential of van der waals forces and Pauli's exclusion principle between two non bonded interacting atoms. The energy obtained from this calculation was -41.07531759 which is confirmed to be correct by the script.

Experimental

The grid of k-points on which the states are averaged is known as the 'shrinking factors'. 11 shrinking factors were tested to see where the free energy converged, the larger the grid, the more accurate the energy values, however the slower the calculation. As such, a compromise was to be made between accuracy and speed. A suitable k-space grid was determined empirically by calculating the free energy at 300 K for various grid sizes.

In order to calculate the thermal expansion coefficient, the volume for a range of temperatures between 0 K and and 2500 K was calculated and plotted, the gradient was determined and is shown below with a plot of the lattice constants as well.

For the molecular dynamics simulation, a supercell of 32 MgO primitive cells was used to increase the accuracy of the calculation as the potential energy surface (PES) is dependant on the relative motion of all the atoms. The shrinking factor used was 1 as since the system in reciprocal space would be 32 times smaller than the one used in quasi-harmonic approximation, hence a shrinking factor of 1 sufficed. This was also done with 24 different temperatures between 100K and 3100K, the volume was plotted against temperature and $\alpha$ was calculated.

Results and discussion

Calculating Lattice vibrations - the phonon modes of MgO

The vibrational (phonon) modes of the MgO crystal were computed and the dispersion curves are shown below. These curves show the variation of frequencies as a function of k, where k is the wavevector of the vibration.

$k=\frac{2\pi }{\lambda }$

The density of states (DOS) for a 1x1x1 grid was computed for a single k-point. The intensity of the first two peaks in the DOS graph is approximately double that of the final two peaks, there are thus more dense states at lower frequencies; since this is a 2 atom system in 3D, we expect 6 total branches, which can be seen in the phonon dispersion curve. from the DOS, the corresponding k-point should be doubly degenerate at around 300 and 350 cm^-1 as well as two other states at around 700 and 800 cm^-1 it is thus point L that was chosen to be the k-point of the DOS. Also, in the log file the k-point that was used was the k-point at (0.500000,0.500000,0.500000) in k-space, corresponding to point L.

As shown in table 1 below, the greater the grid size, the greater the resolution and hence the smoother and more accurate the DOS curve, more peaks are also visible. As the grid size approaches 32x32x32, the difference in the shape of the DOS curve decreases and the shape converges. As such, it was assumed that a grid size of 32x32x32 was a reasonable approximation, this was confirmed by the free energy calculation below. As shown in the DOS there is a large, broad peak at ~ 400 cm^-1 and more visible states than the DOS with a smaller grid size.

Figure 2: MgO phonon dispersion curve

The DOS can be seen to be proportional to the inverse of the derivative of the phonon dispersion curve; as such, when the gradient is small and the curve is converging, there are more states at that frequency, otherwise the DOS is relatively smaller.

Table 1: DOS of different grid sizes

Grid size	DOS
1x1x1
2x2x2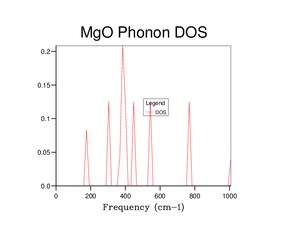
3x3x3
4x4x4
8x8x8
16x16x16
32x32x32
64x64x64

Comparing this lattice structure with other crystals of the same type (fcc) and similarly sized atoms, the same grid size (32x32x32) should be suitable. For example, for a CaO lattice, the CaO bond length is 1.818 Å and that of MgO is 1.743 Å. As such, the lattice parameter is very similar for both structures since for an fcc lattice structure, the lattice parameter is $\sqrt{2}{a}_0$ where $a_0$ is the bond length. Therefore the lattice parameters are approximately 2.57 Å and 2.46 Å for CaO and MgO respectively. However this grid size would not be suitable for zeolite minerals such as Faujasite, nor would it be suitable for metals. This is because zeolite minerals consist of much larger constituent atoms/molecules, as such, the lattice parameter would be much larger, and therefore the lattice parameter in reciprocal space would be much smaller, so a smaller grid size would be more suitable. For metals, the 'primitive cell' would simply be the metal cation, as such the lattice parameter would be small, and in reciprocal space would be large, so a larger grid size is required.

Computing the free energy - the quasi-harmonic approximation

Figure 3: Plot of free energy in eV vs shrinking factor

As shown in figure 3, the plot of the total free energy in eV vs the shrinking factor shows a rapid decrease in the magnitude (less negative) of the free energy at first between the first 3 grid sizes, then slowly decays to convergence at ~ 32x32x32. The data is shown in Table 1 to 8 significant figures.

Table 2: Free energy of the MgO system using different grid sizes

Shrinking factor	Free energy/eV
1	-40.930301
2	-40.926609
3	-40.926432
4	-40.926450
6	-40.926471
8	-40.926478
10	-40.926480
16	-40.926482
32	-40.926483
40	-40.926483
64	-40.926483

It should be noted that the difference in energy between each grid size decreases with the increase in shrinking factor, thus the suitability of the shrinking factor is dependant on the precision of the energy value required. For example, the difference in energy between grid size 4 and 6 is 0.000021 eV as such this difference in grid size is irrelevant if the precision of the calculation is to 1 meV. When the shrinking factor reaches 10 the difference becomes <= 0.000002 and as such, a grid size of more than 10x10x10 is irrelevant for a precision of 0.5 meV. When the shrinking factor reaches 32 the difference becomes 0.000000 as such, it's accurate to 0.1 meV and to 8 significant figures which is the maximum DLV outputs, it was thus determined that a grid size of 32x32x32 would be used for all future calculations. This only applies to MgO and other crystal structures with similar size constituents such as CaO but not for zeolites or metals for the same reasons discussed above.

The Thermal Expansion of MgO

Figure 4: Plot of Free energy vs. temperature with a 32x32x32 grid size using the quasi-harmonic approximation

Figure 4 shows the total free energy of the system at each calculated temperature, it can be seen that for the first 100 K, the free energy remains relatively constant, but then starts to increase in magnitude (more negative) at higher temperatures with an ever increasing rate. At low temperatures, most of the free energy is coming from the zero point energy contribution since it's temperature independent, whereas the entropic and internal energy contributions increase with temperature.

Figure 5: Plot of the lattice constant vs. temperature of the quasi-harmonic approximation

Similarly, for the lattice constant plot (figure 5) there is no significant change in the lattice constant over the first 100 K, after which, there is an increase with temperature, which is a linear increase at first, however as the temperature approaches the melting point of MgO of 3250 K, the lattice constant (and hence the volume) linearity breaks; assuming a purely harmonic system, no matter how much energy is in the system, the system will remain in the potential well and the average bond length (and hence, volume) will remain constant. However by using the quasi-harmonic approximation, the phonon frequency ${\omega }_k$ is volume dependant so thermal expansion can be modelled, this allows the quasi-harmonic approximation to account for some of the anharmonicity, however at its core it is still assumed that the system is purely harmonic at each volume, thus it breaks down at higher temperatures as it does not account for phase changes due to a lack of anharmonicity.

Figure 6: Plot of the linear region (between 400 K and 1500 K) of the Cell volume vs temperature quasi-harmonic approximation

Considering the linear region from the cell volume/lattice constant plot, the expansion coefficient, $\alpha$, can be calculated. The gradient was determined to be 0.00241 (3 s.f.). This value along with the initial volume at 400 K (75.730024 ų) were used to calculate the volumetric thermal expansion coefficient which was determined to be 3.18e-5 K^-1 . The linear thermal expansion coefficient is a third of the volumetric coefficient and was calculated to be 10.6e-6 K^-1 which is rather close to the reference value of 12.02e-6 K^-1. The discrepancy could be due to the quasi-harmonic approximation, which assumes that the two atoms are always inside the harmonic potential well and thus no bonds will break even at infinite temperatures!

Molecular Dynamics

Figure 7: Molecular dynamics plot of cell volume vs. temperature

Figure 8: Linear regression of the molecular dynamics linear region between 400 K and 1500 K.

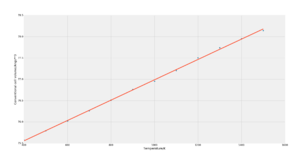
The molecular dynamics simulation is based in Newton's laws of classical mechanics, as such the zero point energy is not considered; this was confirmed by the inability of GULP to perform the calculation at 0 K, another reason GULP gave an error at 0 K could be because the volume was essentially zero. As such, the simulation was started from 100 K and upwards.

Again, it was decided that the most linear region was that between 400 K and 1500 K. The gradient was calculated to be 0.00239, which means that the volumetric thermal expansion coefficient was determined to be 31.5e-6 K^-1 and the linear coefficient 10.5e-6 K^-1 which is essentially identical to the value obtained from the quasi-harmonic approximation approach.

Similarly to the quasi-harmonic approximation calculation, the molecular dynamics simulation produced a linear volume/temperature plot (figure 7) which broke down at high temperatures. This is because the simulation becomes noisy. At high temperatures, the kinetic energy gained by the atoms becomes much larger such that the vibrations become too fast. Since the simulation is executed through a stepwise algorithm, and the velocities and displacements fluctuate much more and much faster at higher energy, the time steps chosen are no longer sufficient to capture the systems properties accurately, smaller step intervals would be needed.

Figure 9: Comparison plot between the quasi-harmonic approximation and molecular dynamics simulation

In contrast to the quasi-harmonic approximation, the molecular dynamics simulation does take into account anharmonicity effects, however it still breaks down at high temperatures for the aforementioned reasons.

Conclusion

The thermal expansion coefficient gives great insight into the properties of a crystal lattice regarding how it behaves on heating. The coefficient was calculated successfully using two different techniques - the quasi-harmonic approximation and molecular dynamics which gave values of 10.6e-6 K^-1 and 10.5e-6 K^-1 for the linear expansion coefficient respectively. This matched well with the experimental reference value of 12.02e-6 K^-1 which shows that the computations were successful. A larger shrinking factor or supercell could have made the calculations more accurate, however the CPU time would have exceeded the time constraints. These simulations could be applied to other lattices of similar sizes such as a CaO lattice.