Rep:Mod:ha3915TS

Transition States and Reactivity Computational Lab

Introduction

Potential Energy Surface

Figure 1: A potential energy surface with labels to describe the properties of a transition state

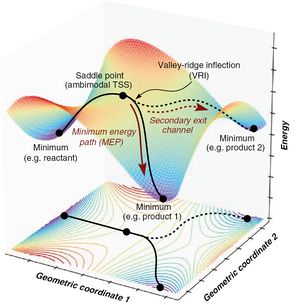
A potential energy surface (PES) is a depiction of the relationship between a reaction's geometry parameters and the potential energy. The dimensionality of such surface is determined by 3N-6, where N is the number of atoms involved in the reaction. As such the dimensionality is proportional to the number of degrees of freedom of the molecule. Although the PES is found for multiple progress variables, one can minimise all other degrees of freedom such that only one reaction coordinate remains variable, giving the energy profile of the reaction.

A Transition State (TS) is a maximum on the minimum energy pathway; this is usually the pathway taken by the reaction where the reactants and products are minima with the maximum transition state between them. It is thus a saddle point on the multi-dimensional PES as all second derivatives are positive except that of the reaction coordinate.

All stationary points on the PES have first derivatives of 0 with respect to all degrees of freedom. For a minimum point, the second derivative will be positive since it describes the curvature of the surface and any fluctuation at a minimum will cause an increase in the potential energy since it has a positive curvature. The opposite case, where the curvature is negative, describes a maximum; any fluctuation would decrease the potential energy. A TS is a saddle point, only some fluctuations cause a decrease in energy whilst others can cause an increase in energy. Since the TS is a maximum on the energy profile it will have a negative curvature (negative second derivative) with respect to one degree of freedom (the reaction coordinate that gives the minimum energy pathway or energy profile) and positive curvature (positive second derivative) for all other degrees of freedom. The matrix of partial second derivatives of a multivariable function is known as the Hessian matrix, as such, the eigenvalues of the matrix can be examined to determine the curvatures at each point.

Nf710 (talk) 09:21, 8 March 2018 (UTC) In each dimension*

Such an energy landscape can be dense with saddle points, however only a few are relevant transition states, since by definition, the transition state is a saddle point on the PES with a single negative Hessian eigenvalue.

The negative Hessian eigenvalue means that the force constant for that vibration is negative. The vibrational frequency is calculated by:

$\nu =\frac{1}{2\pi c}\sqrt{\frac{k}{\mu }}$

where ν is the wavenumber, c is the speed of light, k is the force constant and µ is the reduced mass. As such, the vibrational frequency is imaginary; thus every TS has an imaginary vibrational frequency; this phenomenon was used to confirm the success of the calculations.

Nf710 (talk) 09:21, 8 March 2018 (UTC) A TS is a first order saddle point. upon diagonalisation of the Hessian the normal modes are the eiegenvectors. its is along these vectors which are linear combinations of the degrees of freedom that you move when you see a vibration. As the degrees of freedom are all changing at the same time.

Computational Methods

Three methods were used to locate the transition state of the reaction as described in the tutorial, these were:

1. Guessing a transition state, then placing the reactants in a similar position and orientation, then optimise - some transition state may be found, however this method is unreliable but it's quick.
2. Similar to method 1, however the bonds which are thought to form during the transition state between the interacting atoms are frozen in length during optimisation - this makes it more likely to find the transition state for more complex reactions but is slower than method 1.
3. The product was drawn and optimised to a minimum, the bonds which are thought to be formed in the reaction are broken and frozen as above in 2. Then the transition state was calculated - this method was the most successful but was the slowest.

In order to optimise the geometry of the transition state, Gaussian did step-wise calculations for the single point energy as an attempt to solve the Hamiltonian matrix of the system for each possible geometry until the energy converged and the minimum energy structure was found.

Gaussian assumes the linear combination of atomic orbitals to calculate MO energies - this is defined mathematically as $|\mathrm{\Psi }>=\sum _i^N{c}_i{\mathrm{\Phi }}_i$ , where φ_i is the atomic orbital, c_i is a weighting coefficient and |Ψ> the wavefunction vector in Hilbert space. This is done using the Hamiltonian, which in bra-ket notation is defined as $E=<\mathrm{\Psi }|H|\mathrm{\Psi }>$

To solve the Hamiltonian matrix, two different algorithms were used. PM6 and B3LYP. PM6 is a semi-empirical method in which some terms in the matrix are assumed by approximation. As such, the optimisations are less accurate than B3LYP. B3LYP however, utilises a 6-31G(d) basis set and is a DFT-hybrid technique (Density Functional Theory and the Hartree-Fock methods); this means that the Hamiltonian matrix is solved as a function of electron density and there are no integral approximations; B3LYP also accounts for the exchange integral and the electron correlation exchange energy. Both methods utilise the Hartree-Fock method, which uses a set of electron wavefunctions to approximate the motion of electrons in a field of atomic nuclei by assuming that the wavefunction can be approximated by a single Slater determinant (an expression that describes a multi-fermionic (electrons are fermions) and satisfies Pauli's exclusion principle) made up of one spin orbital per electron. Since B3LYP is a hybrid many more properties of the system can be determined more accurately; Hartree-Fock is a quantum mechanical method of approximation that best describes the exchange correlation but can't determine the dynamic electron correlation accurately, this is where DFT is used - which can exactly determine the dynamic electron correlation is used.

Nf710 (talk) 09:28, 8 March 2018 (UTC) Great understanding of the methods. particularly about the electron correlation. And the antisymetry of the electron. Some equations of the hamiltonians for DFT and HF would have been cool.

Exercise 1: Reaction of Butadiene with Ethylene

(Fv611 (talk) Very good, concise discussion across the whole exercise. Well done!)

This Diels Alder reaction was investigated using PM6 to determine the transition state. This was achieved by using method 2 mentioned above. Figure 2 shows the reaction scheme:

Figure 2: Reaction Scheme and mechanism for the Diels Alder reaction of Butadiene with Ethylene

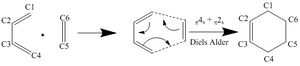
This pericyclic cycloaddition reaction has a _π4_s and a _π2_s component (butadiene and ethylene respectively) and is thus thermally allowed as satisfied by the Woodward-Hoffman rules.

Upon transition state optimisation, an Intrinsic Reaction Coordinate  (IRC) calculation was performed, again with PM6, to confirm that a transition state has been found. The IRC results and MO diagram are shown below.

Figure 3: IRC Path for exercise 1 - Butadiene and ethylene

MO Analysis

Figure 4: MO Diagram for exercise 1 - Butadiene and ethylene

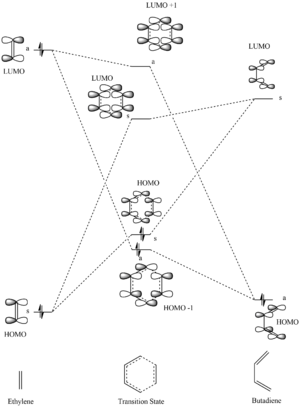
According to frontier molecular orbital theory, the transition state orbitals are formed by the interactions of the frontier orbitals of the reactants (the HOMO and LUMO). The MOs of the reactants and TS are shown below, matching those depicted in the MO diagram. The relative energy positions of these orbitals were calculated through a single point energy calculation. The labels "s" and "a" in the MO diagram describe whether the MO is symmetric or asymmetric.

It can be seen that the butadiene HOMO interacts with the LUMO of the ethylene as they are of the same symmetry. This results in the formation of a transition state bonding/antibonding pair (the HOMO - 1 and the LUMO + 1) which are of the same symmetry as the interacting reactant orbitals, antisymmetric. Likewise, the symmetric ethylene HOMO interacts with the butadiene LUMO to form a further two symmetric transition state orbitals.

It is important to note that only orbitals of the same symmetry interact to form transition state orbitals of the same symmetry as the reactants' interacting orbitals. This is due to the overlap integral being non-zero, only when the two interacting orbitals are of the same symmetry. The overlap integral is defined as:

$S_{P_A,P_B}=\int {\mathrm{\Psi }}_A{\mathrm{\Psi }}_{B}dV$

Where ${\mathrm{\Psi }}_A$ and ${\mathrm{\Psi }}_B$ are orbital wavefunctions. In order to achieve a non-zero integral the integrated function must not be odd; this is true when the symmetry of the orbitals is the same, as such, the integrand becomes even and there is constructive interference so the orbitals can interact.

This reaction follows a 'normal electron demand' for a Diels Alder reaction as the HOMO of the diene and the LUMO of the dienophile (the asymmetric fragment orbital pair) have the largest splitting when forming the transition state MOs.

The MOs for the reactants and the transition state are shown below:

Butadiene HOMO

Butadiene LUMO

Ethylene HOMO

Ethylene LUMO

TS HOMO - 1

TS HOMO

TS LUMO

TS LUMO + 1

Bond Length Analysis

Table 1ː Change in C-C bond lengths as the reaction proceeds. The carbons are numbered as they are in the reaction scheme in figure 2.

Carbons	Reactants Bond Length / Angstrom	TS Bond Length / Angstrom	Products Bond Length / Angstrom
C1-C2	1.3334	1.3798	1.5009
C2-C3	1.4706	1.4111	1.3370
C3-C4	1.3334	1.3798	1.5008
C4-C5	N/A	2.1143	1.5372
C5-C6	1.3273	1.3818	1.5346
C6-C1	N/A	2.1151	1.5372
Literature values for bond lengths: Butadiene C-C: 1.454 ; Butadiene C=C: 1.338 ; Ethene C=C: 1.331

From this data it can be seen that in the product, there is one double bond where as in the reactants there are three; this agrees with the reaction scheme and the mechanism as predicted in figure 2.

The bond lengths in the transition state are not traditional as with the literature values; this is because the double bonds elongate as they become single bonds - the bond lengths are therefore intermediate between a single and double bond. This represents a change in hybridisation from sp2 carbons to sp3 carbons.

However in the C2-C3 pair a double bond is formed when electrons are moved during the pericyclic reaction, thus the bond gets shorter in the transition state to become of double bond length in the products. This can be rationalised by Hammond's postulate which states that the transition state of a reaction resembles either the reactants or the products depending on which it is closer to in energy; in this case, as confirmed by the IRC path in figure 2, the transition state resembles the product.

The Van der Waals radius of a carbon atom is 1.7 Å. In the transition state, the bond length of the newly formed bonds are 2.115 Å which is less than 2x1.7, suggesting that a bond is actually forming and there are attractive interactions between the two atoms so a sigma bond can form.

Vibrational TS Analysis

The JSmol below shows the imaginary transition state vibration as discussed in the introduction.

This shows the butadiene carbons getting closer to the ethylene; since symmetry is maintained throughout the vibration, both fragments must be moving at the same rate. the bond forming process is therefore synchronous which confirms the concerted nature of Diels Alder reactions. This is confirmed by the IRC animation of the reaction below.

Figure 5: IRC animation for the formation of cyclohexene from butadiene and ethylene

LOG files

Butadiene

Ethylene

Transition State

Exercise 2: Reaction of Cyclohexadiene and 1,3-Dioxole

This reaction is another Diels Alder cycloaddition which is thermally allowed, however in this case, the addition could be endo or exo depending on the approach trajectory of the reactants and their geometrical orientation, this is shown in the reaction scheme below.

Figure 6ː Reaction scheme for the reaction of cyclohexadiene and 1,3-Dioxole showing the exo and endo products.

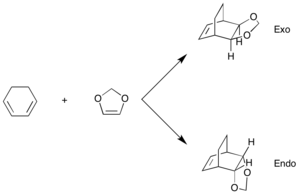
MO Analysis

Figure 7: MO diagram for the reaction of cyclohexadiene and 1,3-Dioxole in both conformations. Endo as shown in the black lines and Exo shown in red.

(Fv611 (talk) Very nice MO diagram.)

The MO diagram above shows the MOs and relative energies for both the Endo (black) and Exo (red) reactions.

This reaction follows an 'inverse electron demand' as the diene LUMO/ dienophile HOMO gap is smaller than the diene HOMO/dienophile LUMO gap. This could be rationalised by the presence of electron donating oxygen atoms in the Dioxole being able to donate more electron density into the pi bond; thus raising the HOMO and LUMO energies of the dienophile. It should also be noted that the Exo TS has a higher energy HOMO and a lower energy LUMO comparing to the Endo.

Nf710 (talk) 09:31, 8 March 2018 (UTC) How do you know this? You have just stated it and not given any energies or numbers. You can investigate this quantitatively if you do a single point energy calculation.

Cyclohexadiene HOMO

Cyclohexadiene LUMO

1,3-Dioxole HOMO

1,3-Dioxole LUMO

Exo TS HOMO-1

Exo TS HOMO

Exo TS LUMO

Exo TS LUMO+1

Endo TS HOMO-1

Endo TS HOMO

Endo TS LUMO

Endo TS LUMO+1

Energy Analysis

The LOG files produced by Gaussian were inspected for the Gibbs free energy, which is the sum of electronic and thermal free energies. These energies are shown below

Table 2ː Gibbs free energy values of reactants and transition states

Molecule	Gibbs Free Energy / Eh
Cyclohexadiene	-233.324
1,3-Dioxole	-267.068
Exo TS	-500.329
Endo TS	-500.332

The reaction barrier was then calculated by subtracting the energy of the reactants from the transition state energy for each of the products. The results are shown in the table below.

Reaction	Reaction Barrier / kJ mol-1	Overall Reaction Energy / kJ mol-1
Exo	166.310	-65.154
Endo	158.467	-68.749

Table 3ː Reaction barriers and energies for Endo and Exo.

These energies were calculated using the B3LYP method and 6-31G(d) basis set. It can be seen from the reaction barrier energy that the Endo TS is lower in energy than the Exo TS (see MO diagram). This suggests that the kinetic product is the Endo product; thus if the reaction was irreversible it would be selective towards the Endo product. The endo product also has a lower overall reaction energy and the endo product is more stable, thus the endo product is also the thermodynamic product. The lower reaction barrier are due to the favourable secondary orbital interactions between the lone pair on each oxygen atom in the p orbital on the dioxole and the π orbitals on the cyclohexadiene, stabilising the TS. In the exo product, the interaction between the O atoms and the π orbitals ceases to exist as they are simply too far away.

There was a large discrepancy between the energies calculated by B3LYP compared with PM6. The B3LYP energies are much more accurate, however a pre-optimisation was done with PM6 to save computational time as B3LYP is much more intensive. This made is easier and quicker to find the minimum as B3LYP was used on an already somewhat optimised structure.

Nf710 (talk) 09:34, 8 March 2018 (UTC) You had some nice Jmols in the section but the discussion is very brief. You got basically the correct energys so have come to the right conclusions it was just not discussed in enough detail.

LOG Files

Cyclohexadiene

1,3-Dioxole

Exo Transition State

Endo Transition State

Exo Product

Endo Product

Exercise 3: Diels-Alder vs Cheletropic

Figure 8ː Reaction scheme for exercise 3 of the Diels Alder (both Endo and Exo) and Cheletropic reactions of SO₂ and Xylylene.

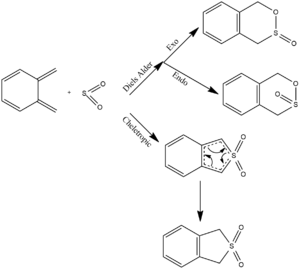
(Be careful: you're showing bonds between S and the Cs in the TS as having bond order 1.5 Tam10 (talk) 10:48, 7 March 2018 (UTC))

The reaction between Xylylene and SO₂ was invesigated. Both Endo and Exo Diels alder reactions were optimised and the transition states calculated. This was again a _π4_s + _π2_s pericyclic reaction and was therefore thermally allowed in accordance with Woodward-Hoffman analysis.

A cheletropic reaction of xylylene and SO₂ was also investigated. This is also a pericyclic reaction, where two new sigma bonds form to the same atom forming the five membered ring as shown in figure 8.

All the calculations were performed using PM6 as it gave relatively accurate geometrical optimisations for the purposes of this investigation. Although the energies are most likely inaccurate.

IRCs were also calculated to confirm the transition state, these are analysed below.

IRC analysis

Figure 9: IRC animation for the formation of the Exo adduct
Figure 10: IRC animation for the formation of the Endo adduct
Figure 11: IRC animation for the formation of the cheletropic product

It can be seen from the IRC animations that the sigma bonds formed in the Endo and Exo Diels Alder reactions are not formed simultaneously; the reaction is thus described to be an asynchronous cycloaddition. On the other hand, the cheletropic IRC shows both bonds forming simultaneously to the S atom; it is thus a synchronous reaction. The formation of the aromatic ring in these reactions is a strong driving force due to the stabilisation energy of aromatics.

Energy Analysis

The table below shows the reaction barrier energies and the overall reaction energies for the three reactions above, these were calculated the same was as in exercise 2 but with the PM6 method.

Table 4ː Reaction barriers and energies for the three reactions.

Reaction	Reaction Barrier / kJ mol-1	Overall Reaction Energy / kJ mol-1
Exo	88.398	-98.531
Endo	84.420	-96.369
Cheletropic	106.734	-153.358

As in exercise 2, the Endo approach is more kinetically favourable as the reaction barrier is smaller, and since this is an exothermic reaction, according to Hammond's postulate, the product is much more likely to be formed. Again, the reaction barrier for the Endo transition state is smaller due to stabilising secondary orbital overlap of the π systems. However in this case, the discrepancy in activation energies between the Endo and Exo reactions is small; this is due to the size of the dienophile (sulfur dioxide) being very small such that the secondary orbital overlap effect is limited.

The Cheletropic reaction has the highest activation energy but the lowest reaction energy; this could be rationalised by considering the stabilisation from the extra S=O double bond in the cheletropic product. This makes it the most favourable thermodynamic product. The high activation barrier can be rationalised by the ring strain in the five membered ring that is formed which is larger compared to the ring strain in the six membered ring that is formed in the Diels Alder reactions.

Endocyclic reaction at alternative site

Figure 12: Reaction scheme for the alternate endocyclic reactions that could occur, both Exo and Endo

Xylylene could also react with SO₂ through its cis-butadiene fragment forming the two possible endocyclic products shown in the reaction scheme above. The transition state for both of these reactions was calculated and an IRC was performed - the IRC animations are shown below

Figure 13: IRC animation for the formation of the endocyclic exo product

Figure 14: IRC animation for the formation of the endocyclic endo product

Since this is also a Diels Alder reaction, it can be seen in the IRC that the bonds don't form simultaneously and is therefore asynchronous.

Energy Analysis

Table 5ː Reaction barriers and energies for the two reactions.

Reaction	Reaction Barrier / kJ mol-1	Overall Reaction Energy / kJ mol-1
Exo	122.472	23.356
Endo	114.642	18.906

Comparing these energies with the exocyclic reactions above, it can be concluded that an endocyclic reaction at the cis-butadiene site is unlikely due to the higher activation energy; this could be rationalised by the increased ring strain. The free energy of the reaction from both endo and exo approaches are positive which means that the reaction is not spontaneous and thus is thermodynamically unfavourable; this could be rationalised by considering the lack of aromatisation as compared with the exocyclic reactions.

Energy profile

Figure 15: Energy profile for the formation of the 5 products

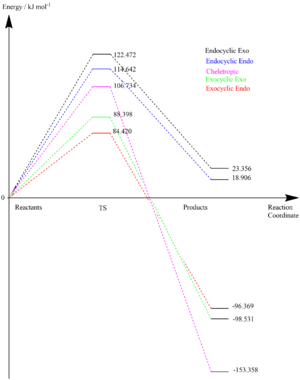
LOG files

Sulfur dioxide

Xylylene

Exo Transition State

Endo Transition State

Exo Product

Endo Product

Cheletropic Product

Cheletropic Transition State

Alternative Exo Product

Alternative Endo Product

Alternative Exo Transition State

Alternative Endo Transition State

Conclusion

PM6 and B3LYP were two methods that were used to attempt to understand a reaction's pathway through optimising and finding transition states. A set of exercises dealing with pericyclic reactions showed that the transition states can be calculated with both methods for complex reactions.

From the exercises, it seems that in most cases, the endo reaction barrier was lower than the exo reaction barrier due to stabilising secondary orbital overlap between the p-orbitals on the dienophile and the diene orbitals. The exo product is also usually the most thermodynamically favourable due to steric hindrance, however as shown in exercise 2, even an exo product can become unfavourable because of sterics as the discrepancy is not large.