Rep:Mod:ha3915
Predicting molecular characteristics by using quantum calculations.
Gaussian and its GUI Gaussview were used to model the electronic structure of molecules and optimise certain molecular properties (such as bond length) based on the calculations so the minimum energy of the molecule was reached. The software used Hybrid Functionals to make the calculations much quicker, more specifically the B3LYP, (Becke, 3-parameter, Lee-Yang-Parr) functional was used.
Calculations and analysis of molecules in the Haber-Bosch Process
NH3
Optimisation
Firstly, the NH3 molecule was created and optimised. Table 1 below shows the values of the characteristics off the molecule after the calculation. The calculation suggests that the lowest energy that an ammonia molecule could have is where the nuclei of the atoms are about 1.01798 Å apart; This is somewhat in agreement with the literature value of the bond length 1.016 Å. The calculated bond angle, 105.7° is also relatively accurate as the literature value is 106.5°[1]. An interactive 3d Model of the ammonia molecule is shown in Figure 1 below, along with the output .Log file from Gaussian.
| Property | Value |
|---|---|
| Molecule | NH3 |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (au) | -56.55776873 |
| RMS Gradient (au) | 4.85 x 10-6 |
| Molecule Point Group | C3V |
| N-H Bond Length (Å) | 1.01798 |
| H-N-H Bond Angle (°) | 105.741 |
| Spin | Singlet |
| Dipole moment (D) | 1.8466 |
This data shows the values of the converging parameters such as force and displacement; these values converge to 0, however there is a threshold determined by Gaussian to allow for rounding errors caused by floating-point operation errors.
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986259D-10
Optimization completed.
-- Stationary point found.
Figure 1: Optimised NH3 |
Get the .Log file here
Molecular Vibrations
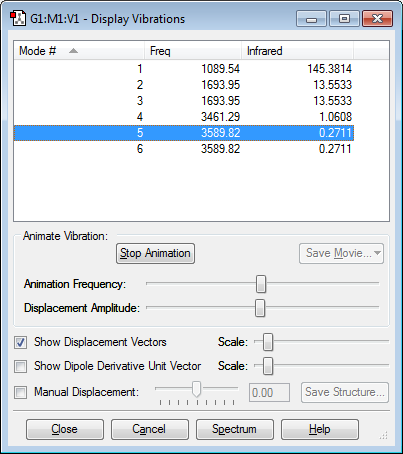
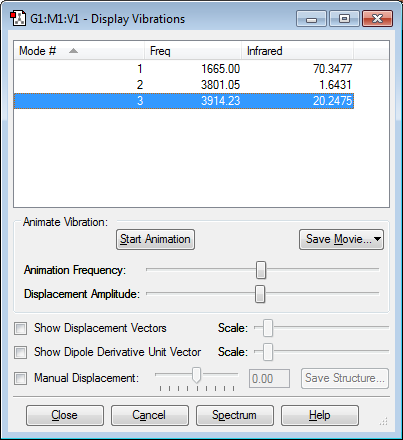
Using the 3N-6 rule for ammonia where N=4, we would expect 6 vibrational modes as proved by the Gaussian calculation and shown in figure 2. It can also be shown that vibrational modes 2 and 3 are degenerate, as well as vibrational modes 5 and 6 as they have the same frequency and therefore the same energy. Modes 1,2 and 3 are bending vibrations due to their low frequencies; where as modes 4,5 and 6 are bond stretch vibrations due to their high frequencies. Mode #4 is highly symmetric as shown in Animation 1 below. Mode #1 is known as the "umbrella" mode as the molecule partly inverts like an umbrella, this is shown in Animation 2 below.

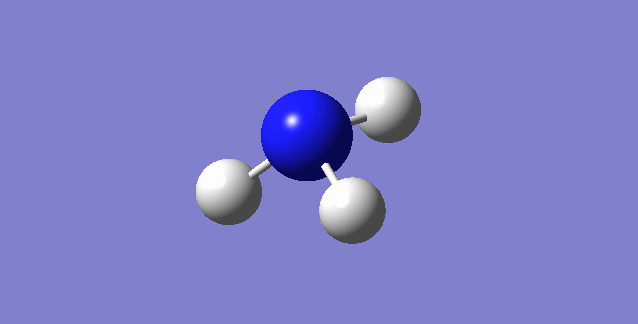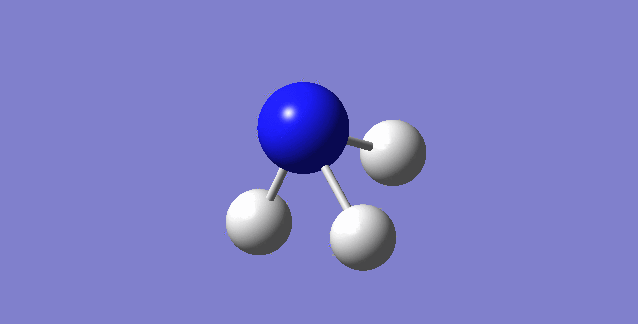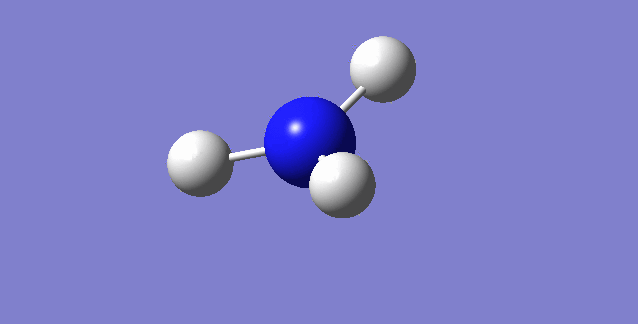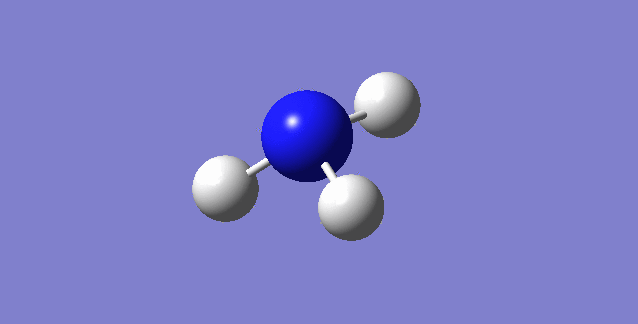
On an experimental spectrum of gaseous ammonia, we would expect to see 2 bands only; this is because modes 2,3 and 5,6 are degenerate, leaving us with 4 bands, however bending vibrations are at such a low frequency that they are not usually seen, leaving us with 2.
| How many modes do you expect from the 3N-6 rule? | 6 |
|---|---|
| Which modes are degenerate (ie have the same energy)? | 2,3 and 5,6 |
| Which modes are "bending" vibrations and which are "bond stretch" vibrations? | 1,2,3 bend 4,5,6 stretch |
| Which mode is highly symmetric? | 4 |
| One mode is known as the "umbrella" mode, which one is this? | 1 |
| How many bands would you expect to see in an experimental spectrum of gaseous ammonia? | 2 |
Charge Analysis
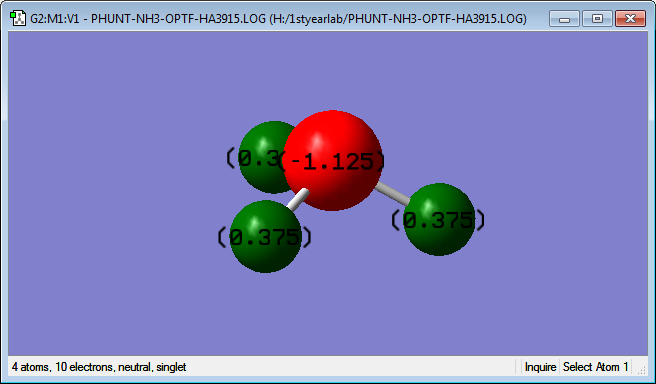
The charge on the Nitrogen atom was calculated to be -1.125, where as the charges on each hydrogen atom were all the same at +0.375; this was expected as it is known that Nitrogen is one of the most electronegative atoms, so all the electron density is attracted to the highly electronegative Nitrogen and pulled away from the less electronegative (more electropositive) Hydrogens.
| Charge on Nitrogen = -1.125 |
|---|
| Charge on H1 = Charge on H2 = Charge on H3 = 0.375 |
| As expected due to difference in electronegativity |
N2
Optimisation
The N2 molecule was also created and optimised. Table 4 below shows the values of the characteristics off the molecule after the calculation. The calculation suggests that the lowest energy that a nitrogen molecule could have is where the nuclei of the atoms are about 1.10550 Å apart; This is in agreement with the literature value of the bond length 1.098 Å[2] considering the error threshold.
| Property | Value |
|---|---|
| Molecule | N2 |
| Calculation Type | FREQ |
| Calculation Method | B3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (au) | -109.52412868 |
| RMS Gradient (au) | 6.0 x 10-7 |
| Molecule Point Group | D∞H |
| NΞN Bond Length (Å) | 1.10550 |
| NΞN Bond Angle (°) | 180 |
| Spin | Singlet |
| Dipole Moment (D) | 0.0000 |
This data shows the values of the converging parameters such as force and displacement; these values converge to 0, again, there is a threshold determined by Gaussian to allow for rounding errors caused by floating-point operation errors.
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401015D-13
Optimization completed.
-- Stationary point found.
Figure 4: Optimised N2 |

Get the .Log file here
Molecular Vibrations
As shown in Figure 4, N2, only has 1 vibrational mode. This is because N2 is a linear molecule and therefore follows the 3N-5 rule. The frequency of the vibration is relatively high, we would therefore expect this stretch vibration to show up on the spectrum, however as it's a linear molecule, the stretch is symmetrical therefore there is no change in dipole moment so no bands appear on the spectrum.
Charge Analysis
Since N2 is diatomic, there is 0 electronegativity difference as both atoms are identical. The electron density is therefore equally distributed along the molecule. So there is no partial charge on either of the nitrogen atoms.
H2
Optimisation
The H2 molecule was also created and optimised. Table 5 below shows the values of the characteristics off the molecule after the calculation. The calculation suggests that the lowest energy that a hydrogen molecule could have is where the nuclei of the atoms are about 0.74279 Å apart; this is in agreement with the literature value of the bond length 0.741 Å[3] considering the error threshold.
| Property | Value |
|---|---|
| Molecule | H2 |
| Calculation Type | FREQ |
| Calculation Method | B3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (au) | -1.17853936 |
| RMS Gradient (au) | 1.7 x 10-7 |
| Molecule Point Group | D∞H |
| H-H Bond Length (Å) | 0.74279 |
| H-H Bond Angle (°) | 180 |
| Dipole Moment (D) | 0.0000 |
| Spin | Singlet |
This data shows the values of the converging parameters such as force and displacement; these values converge to 0, again there is a threshold determined by Gaussian to allow for rounding errors caused by floating-point operation errors, however this time, some of the values are exactly 0.
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
Figure 6: Optimised H2 |
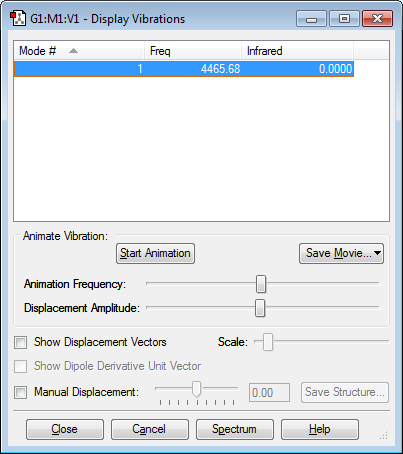
Get the .Log file here
Molecular Vibrations
As shown in Figure 6, H2, only has 1 vibrational mode. This is because H2 is a linear molecule and therefore follows the 3N-5 rule. The frequency of the vibration is relatively high, we would therefore expect this stretch vibration to show up on the spectrum, however as it's a linear molecule, the stretch is symmetrical therefore there is no change in dipole moment so no bands appear on the spectrum.
Charge Analysis
Since H2 is diatomic, there is 0 electronegativity difference as both atoms are identical. The electron density is therefore equally distributed along the molecule. So there is no partial charge on either of the hydrogen atoms.
Haber-Bosch Process energy calculation
The Haber-Bosch Process is one of the most important processes to produce ammonia industrially. Ammonia is used intensively in farming as fertilliser.
The Haber-Bosch Process:
N2 + 3H2 → 2NH3
| Species | Energy (au) |
|---|---|
| NH3 | -56.55776873 |
| 2NH3 | -113.11553746 |
| N2 | -109.52412868 |
| H2 | -1.17853936 |
| 3H2 | -3.53561808 |
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= - 0.0557907 = - 146.47848285 kJ/mol
Calculations of molecular orbitals and optimisation of a water (H2O) molecule
Finally, a water molecule was created and optimised. The first 12 molecular orbitals were calculated and 5 of them are displayed in the figures below. Table 7 shows the properties of the water molecule after optimisation. The calculation suggests that the lowest energy that a water molecule could have is where the nuclei of the atoms are about 0.96522 Å apart; This is somewhat in agreement with the literature value of the bond length 0.9578 Å. The calculated bond angle, 105.7° is also relatively accurate as the literature value is 104.478°[4]. An interactive 3d Model of the water molecule is shown in Figure 8 below, along with the output .Log file from Gaussian.
Optimisation
| Property | Value |
|---|---|
| Molecule | H2O |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (au) | -76.41892999 |
| RMS Gradient (au) | 6.84 x 10-3 |
| Molecule Point Group | C2V |
| O-H Bond Length (Å) | 0.96522 |
| H-O-H Bond Angle (°) | 103.745 |
| Spin | Singlet |
| Dipole moment (D) | 1.9531 |
This data shows the values of the converging parameters such as force and displacement; these values converge to 0, however there is a threshold determined by Gaussian to allow for rounding errors caused by floating-point operation errors. It should be noted that the values obtained here are relatively higher than those in the previous molecules.
Item Value Threshold Converged?
Maximum Force 0.000099 0.000450 YES
RMS Force 0.000081 0.000300 YES
Maximum Displacement 0.000128 0.001800 YES
RMS Displacement 0.000120 0.001200 YES
Predicted change in Energy=-1.939669D-08
Optimization completed.
-- Stationary point found.
The figure Below shows a 3d model of the water based on the output .Log file from Gaussian which is also attached below.
Figure 8: Optimised H2O |
Get the .Log file here
Molecular Vibrations
According to the 3N-6 rule (which we should use as water is not linear) where N=3, we would expect water to have 3 vibrational modes which gaussian successfully predicts as shown in figure 8. The vibrations are also shown in the animations below. There is an antisymmetric stretch, a symmetric stretch and bending vibrational mode as shown in the animations.

However we only see 2 peaks on the spectrum of water as shown below
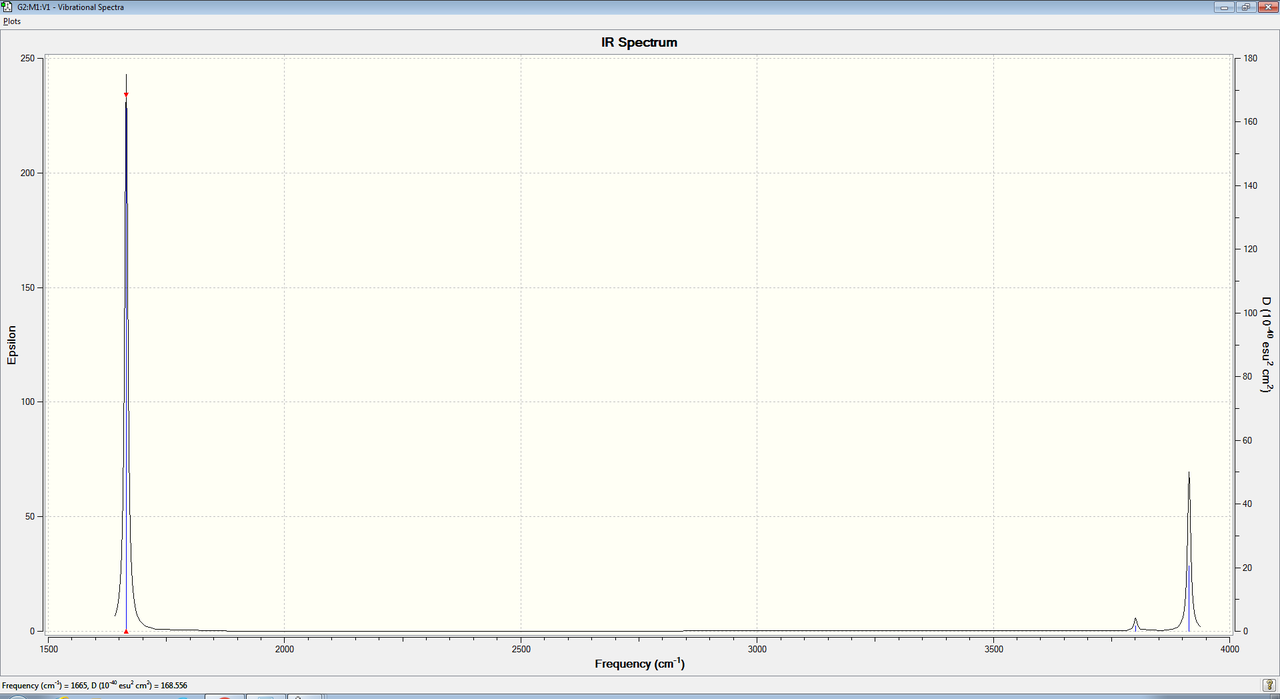
This is because one of the modes has such a small frequency and has such a small change in dipole moment that it can barely be seen on the spectrum.
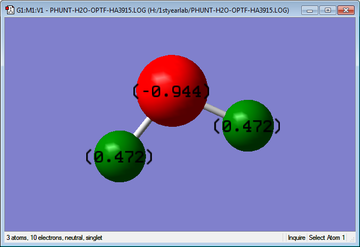
Charge Analysis
The charge on the Oxygen atom was calculated to be -0.944, where as the charges on each hydrogen atom were all the same at +0.472; this was expected as it is known that Oxygen is one of the most electronegative atoms, so all the electron density is attracted to the highly electronegative Oxygen and pulled away from the less electronegative (more electropositive) Hydrogens. Although Oxygen is more electronegative than Nitrogen, the charge on the Oxygen in water is less negative than that of the Nitrogen in ammonia; this is because there are three Hydrogens in ammonia where Nitrogen can pull electron density from, whereas there are only two Hydrogens in water so less electron density is pulled by the Oxygen.
Molecular Oribitals

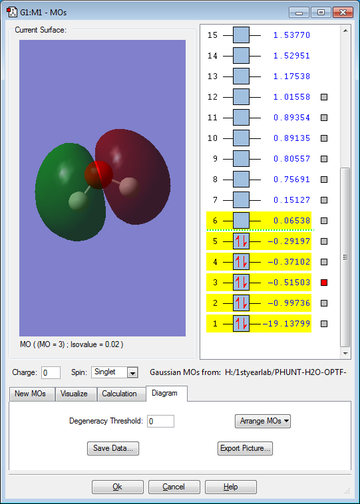

The 5 molecular orbitals (and their energies) shown in figures 12-16 are the lowest energy molecular orbits (excluding the 1s molecular orbital of the oxygen). The molecular orbital diagram is also shown below (figure 17). The 1s orbital on the Oxygen is so low in energy (it is therefore the most stable orbital) that it does not really contribute to bonding since the electrons in the orbital are held very closely to the oxygen atom.
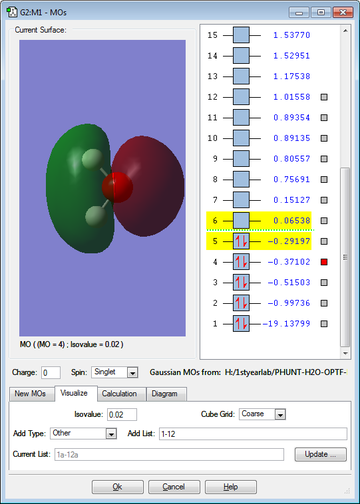

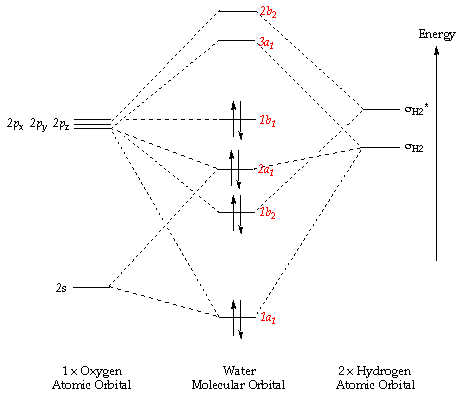
MO2 is formed from the 2s on the Oxygen and the σ MO of the H-O bond; this forms a full bonding orbital and an empty, high energy anti-bonding orbital, MO3, MO4 and MO5 are formed from the set of 2p orbitals (2px, 2py, 2pz), the 2 and they are also involved in both bonding and anti-bonding orbitals of MO2. MO5 is also known as the HOMO (Highest Occupied Molecular Orbital). MO6 is the LUMO (Lowest Unoccupied Molecular Orbital). The energy of this Orbital dictates the reactivity of the molecule and determines whether the molecule is a nucleophile or an electrophile; in this case (with water) the LUMO is so high in energy that it is unlikely to find a molecule with a HOMO with a similar energy, it is therefore not really susceptible to attack by nucleophiles. Water is a good nucleophile itself as the HOMO is of similar energy to the LUMOs of many different molecules.
References
- ↑ Pakiari AH, Nazari F. The study of relationship between chemical geometry and electronic configuration, non-Walsh type B Part II. J Mol Struct THEOCHEM. 2005;717(1-3):189–97.
- ↑ Chattopadhyay S, Chaudhuri RK, Mahapatra US. Application of improved virtual orbital based multireference methods to N2, LiF, and C4H6 systems. J Chem Phys. 2008;129(24).
- ↑ The Journal of Chemical Physics 105, 9200 (1996); doi: 10.1063/1.472753
- ↑ http://cccbdb.nist.gov/exp2.asp?casno=7732185
- ↑ http://www.ch.ic.ac.uk/vchemlib/course/mo_theory/
