Rep:Mod:green88
Introduction
Molecular mechanics is becoming increasingly useful in its ability to accurately model structure, explain observed reactivity and even predict outcomes of reactions, which could be accomplished without physically interacting with potentially dangerous chemicals and could be a more cost-effective and energy-efficient process as no chemicals need to be synthesised or disposed of. However, the disadvantages of this method are that the calculations come from known molecules so is limited in its scope in that the data cannot be extrapolated. In this case, quantum mechanical methods are considered more appropriate.
In the first part of this report, molecular modelling was used to investigate the structure and spectroscopic properties (1H NMR and 13C NMR) of small and medium-sized organic molecules. The second part contains the use of molecular mechanics in an attempt to assign the absolute configuration of chiral compounds.
The programmes that were used include:
- ChemDraw Pro - To draw 2D structures that were then imported into Avogadro.
- Avogadro - To give 3D coordinates to the 2D structures drawn in ChemDraw then optimise geometry (using the MMFF94s force field, which was introduced to match the accuracy of the MM3 force field across a wide range of organic molecules, including proteins)[1], calculate energies that are only suitable for comparison between different isomers or after a simple reaction and generate files to be input into the HPC for more complex calculations.
- Gaussian - To open the files from the HPC and show predicted spectra.
- Conquest - To search the Cambridge Crystal Database.
- Mercury - To analyse the crystal structure of compounds found in the Cambridge Crystal Database.
The HPC Portal was also used to run more complex calculations.
Part 1
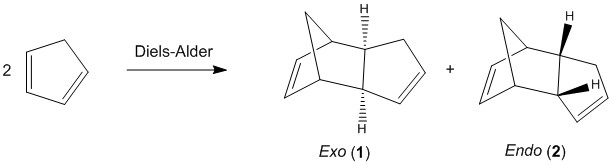
The Hydrogenation of Cyclopentadiene Dimer
In this part of the report, the objectives were to identify the major product of the dimerisation of cyclopentadiene (the kinetic endo product or the thermodynamic exo product) then predict the regioselectivity of the hydrogenation of the cyclopentadiene dimer.
Endo and Exo Isomers of Dicyclopentadiene
The dimerisation of cyclopentadiene is a common example of the Diels-Alder reaction with a [π4s+π2s] cycloaddition combined with a [π2s+π4s] cycloaddition, indicating a concerted bipericyclic reaction.


The structures of 1 and 2 shown above were first drawn in ChemDraw Pro then opened in Avogadro in order to optimise the geometry using the MMFF94s force field option. The energies were then calculated in order to give a comparison of the two isomers as this result cannot directly be used to calculate any thermodynamic quantity.
In literature, the endo form is considered to be the major product with more of the exo product formed by increasing the temperature. This stereospecificity is explained by Alder's endo rule (the "principle of the maximum accumulation of unsaturated centres") because of the favourable secondary orbital interactions facilitating the endo approach. [2]
| Energy Contribution (kcalmol-1) | Exo (1) | Endo (2) | Difference |
|---|---|---|---|
| Bond Stretching Energy | 3.542 | 3.467 | -0.075 |
| Angle Bending Energy | 30.773 | 33.191 | 2.418 |
| Stretch Bending Energy | -2.041 | -2.082 | -0.041 |
| Torsional Energy | -2.730 | -2.950 | -0.220 |
| Out of Plane Bending Energy | 0.015 | 0.022 | 0.007 |
| Van der Waals Energy | 12.801 | 12.358 | -0.443 |
| Electrostatic Energy | 13.013 | 14.184 | 1.171 |
| Total Energy | 55.373 | 58.191 | 2.818 |
Calculations have demonstrated that the exo product is lower in energy, as expected for the thermodynamic product. The main contribution to this energy difference is the angle bending energy which does account for the most deviation from ideality for both molecules.
Therefore, the kinetic product is favoured due to a much lower transition state, most likely lowered by the secondary orbital interactions available in the endo approach. With heating, however, there is sufficient energy for a large population of the molecules to overcome the higher thermodynamic transition state and give the exo product.
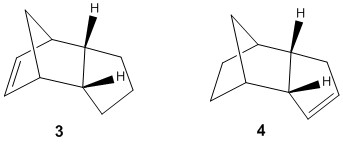
Hydrogenation of Endo Dicyclopentadiene


The endo dicyclopentadiene has two double bonds that can be hydrogenated either in the cyclopentene ring (3) or the norbornene double bond (4).
The calculated energies were measured using the same procedure above used for the exo and endo dimers and compared as shown in the table below.
| Energy Contribution (kcalmol-1) | Cyclopentene (3) | Norbornene (4) | Difference |
|---|---|---|---|
| Bond Stretching Energy | 3.306 | 2.823 | -0.483 |
| Angle Bending Energy | 30.855 | 24.686 | -6.169 |
| Stretch Bending Energy | -1.926 | -1.657 | 0.269 |
| Torsional Energy | 0.076 | -0.378 | -0.454 |
| Out of Plane Bending Energy | 0.015 | 0.000 | -0.015 |
| Van der Waals Energy | 13.275 | 10.637 | -2.638 |
| Electrostatic Energy | 5.121 | 5.147 | 0.026 |
| Total Energy | 50.723 | 41.257 | -9.466 |
According to the calculated energies in the table above, 4 is more stable than 3, indicating that the norbornene double bond is hydrogenated first. The largest difference is found in the angle bending energy which accounts for 65% of the energy difference but this is partially offset by slight increases in the electrostatic and bend stretching energies. Both products are lower in energy than the starting endo dimer, suggesting they are both exothermic reactions.
This is supported in literature which found that the norbornene double bond was hydrogenated more than 5 times faster [3]
Atropisomerism in an Intermediate of the Synthesis of Taxol
Atropisomers are defined by IUPAC as a "subclass of conformer which can be isolated as separate chemical species and which arise from restricted rotation about a single bond"[4]


Taxol is an anti-cancer drug that works by slowing cell-growth and was originally extracted from the Pacific Yew Tree but now total chemical synthesis of the drug is possible [5]. An intermediate in the synthesis of taxol is capable of atropisomerism where the carbonyl oxygen is either up or down. Their geometries were optimised using Avogadro in a similar procedure to what was used above and their energies compared to identify the more stable atropisomer.
For cyclohexane rings, the conformations with the minimum energy are usually the chair and twist boat structures (with the half-chair and boat conformations as energy maxima). However, it was not possible to optimise a geometry of the taxol intermediates into their enantiomeric forms of the chair and twist-boat structures and keep both the protons on the cyclohexane ring in the correct syn orientation.
| Energy Contribution (kcalmol-1) | 9 (Chair) | 9 (Twist Boat) | 10 (Chair) | 10 (Twist Boat) |
|---|---|---|---|---|
| Bond Stretching Energy | 7.661 | 7.950 | 7.604 | 7.800 |
| Angle Bending Energy | 28.277 | 29.496 | 18.826 | 19.797 |
| Stretch Bending Energy | -0.077 | 0.081 | -0.139 | -0.109 |
| Torsional Energy | 0.261 | 2.770 | 0.173 | 4.386 |
| Out of Plane Bending Energy | 0.971 | 0.951 | 0.843 | 0.974 |
| Van der Waals Energy | 33.149 | 34.722 | 33.307 | 34.407 |
| Electrostatic Energy | 0.300 | 0.316 | -0.058 | -0.018 |
| Total Energy | 70.542 | 76.288 | 60.555 | 67.238 |
Unlike the molecules discussed in earlier sections, in all of these conformers the main contribution to their energy comes from the van der Waals' forces, suggesting these forces become more significant as the molecule grows larger. The most stable atropisomer on the basis of comparing their relative energies is the chair form of 10 with the carbonyl oxygen pointing down. The main difference in energies is due to the angle bending energy (accounts for 94.6% of the difference) but the difference in electrostatic energies also gave some contribution (3.6%).
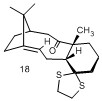
Spectroscopy of an Intermediate Related to Synthesis of Taxol
The final task of the first part of this lab was to predict the 1H NMR and 13C NMR spectra of one of the intermediates shown to the right in the synthesis of taxol (and derivatives of 9 and 10 seen in the previous section). Intermediate 18 was chosen as it was predicted (based on the data from the previous task) that this would be lower in energy. After optimising the geometry in Avogadro, a Gaussian Checkpoint File was sent to the HPC using the B3LYP theory and the 6-31G(d,p) basis set.


| Chemical shift from molecular modelling (ppm) | Chemical shifts given in literature (ppm) | Difference (ppm) |
|---|---|---|
| 5.29 (1H) | 5.21 (m, 1H) | 0.08 |
| 3.32 (1H) | 3 - 2.7 (m, 6H) | 0.16 - 0.32 |
| 3.22 (1H) | See above | See above |
| 3.12 (2H) | See above | See above |
| 2.86 (2H) | See above | See above |
| 2.46 (1H) | 2.7 - 2.35 (m, 4H) | -0.24 - -0.07 |
| 2.40 (1H) | See above | See above |
| 2.28 (3H) | See above | See above |
| 2.09 (1H) | 2.20 - 1.70 (m, 6H) | -0.20 - 0.16 |
| 1.97 (2H) | See above | See above |
| 1.86 (2H) | See above | See above |
| 1.68 (2H) | See above | See above |
| 1.62 (1H) | 1.58 (t, 1H) | 0.04 |
| 1.50 (2H) | 1.50 - 1.20 (m, 3H) | 0.16 - 0 |
| 1.42 (1H) | See above | See above |
| 1.36 (1H) | See above | See above |
| 1.16 (1H) | 1.10 (s, 3H) | 0.06 |
| 1.07 (3H) | 1.07 (s, 3H) | 0 |
| 0.97 (2H) | 1.03 (s, 3H) | 0.06 |

| Chemical shift from molecular modelling (ppm) | Chemical shifts given in literature (ppm) | Difference |
|---|---|---|
| 211.73 | 211.49 | 0.24 |
| 148.56 | 148.72 | -0.16 |
| 118.74 | 120.90 | -2.16 |
| 88.98 | 74.61 | 14.37 |
| 67.78, 56.01 | 60.53 | -4.52 - 7.25 |
| 55.49, 50.01 | 51.30 | -1.29 - 4.19 |
| 48.10 | 45.53 | 2.57 |
| 44.12 | 43.28 | 0.84 |
| 41.93 | 40.82 | 1.11 |
| 37.48 | 38.73 | -1.25 |
| 35.21 | 36.78 | -1.57 |
| 30.94 | 35.47 | -4.93 |
| 28.74 | 30.84 | -2.10 |
| 28.56 | 30.00 | -1.44 |
| 25.63 | 25.56 | 0.07 |
| 25.14 | 22.21 | 2.93 |
| 23.29 | 21.39 | 1.90 |
| 20.95 | 19.83 | 1.12 |
The calculated spectra do give a close match to literature values but, particularly for the 1H NMR, this method has only computed the NMR for a static molecule rather than a more realistic model that would include rapid spinning (so there would be more degenerate proton environments) and vibrations that would affect the proton environment. However, the close match indicates that the basis sets are appropriate for optimising the geometry and giving a realistic static view of the molecule.
The HPC also produced a log file that contained energies of the molecules. By submitting the same job to the HPC portal for 17, the two energies are compared in the table below and as predicted above, 18 was more stable.
| Intermediate 17 | Intermediate 18 | Difference |
|---|---|---|
| -4335849.12 | -4335913.36 | 64.24 |
This energy is judged to be significant because it is larger than thermal energy at room temperature. The barrier to rotation could be the steric clash between the methyl group pointing upwards as the carbonyl oxygen on 17 is also pointing upwards.
Part 2
Asymmetric catalyst systems: Shi Catalyst and Jacobsen Catalyst
In the synthetic component of this laboratory experiment (1S), the two catalysts are synthesised then used to carry out epoxidation reactions for two alkenes to give four different chiral alkene epoxides. In this part of the report, computer modelling is used to investigate the catalyst structure, the expected epoxide's NMR and the absolute configuration and interactions in the active site.
The Shi Catalyst
The Shi catalyst is an asymmetric catalyst derived from fructose. The active catalyst is shown below (22) with its precursor (21) in the synthesis by Hanks et al[9].
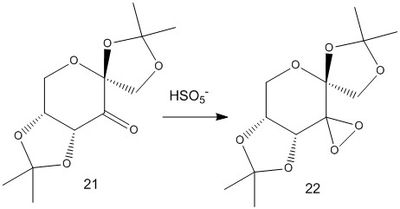
The precursor to the catalyst (21) was investigated using the Cambridge Crystal Database and the anomeric C-O bond lengths were measured in Mercury.

The bond lengths for anomeric C-O bonds ranged from 1.405 to 1.460 and are tabulated below. The reason for the wide range of bond lengths is due to the anomeric effect where for the central carbon, one C-O bond is lengthened (weakened) and the other is shortened (strengthened). This is due to delocalisation of the oxygen lone pair into a carbon-oxygen π-bond.[10]
| Corresponding bond (see diagram above) | Bond length (Å) |
|---|---|
| C14-O8 | 1.405 |
| C14-O12 | 1.420 |
| C21-O7 | 1.406 |
| C21-O8 | 1.460 |
| C22-O10 | 1.442 |
| C22-O11 | 1.430 |
The Jacobsen Catalyst

This precursor appears in the synthesis by Hanson[11] and is known as a stable pre-catalyst.

The pre-catalyst (23) was investigated using the Cambridge Crystal Database (TOVNIB02) and the distance between the tertiary butyl groups of different rings was measured. One was found to be less than the sum of the van der Waals radii (2.363Å), indicating a very close interaction which may be repulsive. This, along with other short H...H distances, sterically blocks the alkene from approaching from this direction.
This picture also shows the short distances between oxygen and protons on the ring (such as 2.238Å) which may indicate that there are hydrogen bonds present stabilising molecules.
Assigning the absolute configurations of the epoxides
For this part of the report, the absolute configurations of the epoxides obtained by using both the catalysts above are predicted using the calculated NMR properties, the calculated chiroptical properties and the properties of the transition state for the reaction. For the first two methods, the epoxidation products of 1,2-dihydronaphthalene and stilbene were investigated and for the last method, β-methyl styrene.
1,2-Dihydronaphthalene
Using the same method as above for the atropisomers, the 1H and 13C NMR were calculated by optimising the geometry in Avogadro, sending the job to the HPC and opening the NMR produced in Gaussview.[12]
The two isomers are shown below.
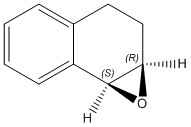
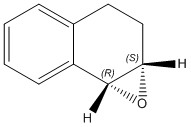
| Chemical shift from molecular modelling (ppm) | Chemical shift from literature (ppm) | Difference (ppm) |
|---|---|---|
| 7.61 (1H) | 7.28 | 0.33 |
| 7.39 (2H) | 7.08-7.17 (m, 2H) | 0.17 - 0.22 |
| 7.25 (1H) | See above | See above |
| 3.56 (1H) | 3.74 (d, 1H) | -0.18 |
| 3.48 (1H) | 3.62 (m, 1H) | -0.14 |
| 2.95 (1H) | 2.68 (m, 1H) | 0.27 |
| 2.27 (1H) | 2.44 (m, 1H) | -0.17 |
| 2.21 (1H) | 2.30 (m, 1H) | -0.07 |
| 1.87 (1H) | 1.65 (m, 1H) | 0.22 |
| Chemical shift from molecular modelling (ppm) | Chemical shift from literature (ppm) [13] | Difference (ppm) |
|---|---|---|
| 135.4 | 136.7 | -1.3 |
| 130.4 | 132.6 | -2.2 |
| 126.7 | 129.5 | -2.8 |
| 123.8, 123.5 | 2 x 128.4 | 4.6 - 4.9 |
| 121.7 | 126.1 | -4.4 |
| 52.8 | 55.1 | -2.3 |
| 52.2 | 52.7 | -0.5 |
| 30.2 | 24.4 | 5.8 |
| 29.1 | 21.8 | 7.3 |
Both the NMR spectra show a close match to the values given in literature, indicating that the geometry was well optimised. However, there are failings of calculating the NMR in this way (especially for 1H NMR) as the calculations are done on a static model rather than one that can take into account vibrations of the molecules and rapid spinning to make more of the atoms degenerate.
| Wavelength (nm) | 3S,4R | Literature value of 3S,4R | 3R,4S | Literature Value of 3R,4S |
|---|---|---|---|---|
| 589 | -52.84 | -39 [16] | 52.76 | 129 [17] |
| 365 | -250.69 | None found | 250.39 | None found |
There is some agreement to literature for the 3S,4R compound but the 3R,4S compound is not close to the value given in literature. However, experimentally it is hard to give a reproducible result for the optical rotation as the property is affected by external factors such as temperature and is also dependent upon its concentration. The change in sign does support the enantiomeric assignment.
Stilbene
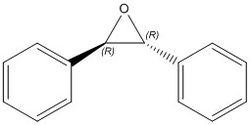



| Chemical shift - E (ppm) | Chemical shift - Z (ppm) | Chemical shift - literature (ppm) |
|---|---|---|
| 7.48-7.57 (10 H) | 7.25 - 7.50 (10 H) | 7.40 - 7.55 (m, 10H) |
| 3.54 (2H) | 4.30 (2H) | 3.95 (s, 2H) |
The literature values are in close agreement with the calculated results for both trans- and cis-stilbene, as expected as experimentally there is likely to be some of the other enantiomer present. The literature cited stated that the trans product was favoured and the chemical shifts of the multiplet seem to agree with this. This does indicate that the optimisation has been successful and can be used to calculate the optical rotary power.


| Chemical shift - E (ppm) | Chemical shift - Z (ppm) | Chemical shift - literature (ppm) |
|---|---|---|
| 134.09 | 131.28 | 137.1 |
| 124.22 | 122.90 | 128.5 |
| 123.52, 123.21 | 122.6 | 125.5 |
| 123.21, 118.26 | 122.3, 122.1 | 125.5 |
| 66.4 | 62.01 | 62.7 |
The 13C NMR is also a close match to literature but there are more peaks than expected, perhaps due to the fact that the calculated NMR is of a static picture and so more carbon atoms may be degenerate than those that are predicted by computer modelling. The 13C NMR of literature is closer to the trans values which does demonstrate the excess of trans product found in the literature.
| Wavelength (nm) | E-Stilbene[21] | Literature value of E-Stilbene[22] | Z-Stilbene[23] | Literature Value of Z-Stilbene[24] |
|---|---|---|---|---|
| 589 | 26.85 | 319.8 | 20.12 | 87.1 |
| 365 | 34.22 | None found | 73.19 | None found |
A comparison to literature suggests that the calculations did not run correctly. If more time was available, the calculations could be run again with a different basis set or method. However, given the wide range of optical rotations dependent on concentration, temperature and other external influences, it could be that the literature value is not completely accurate. Therefore, it is hard to judge if the correct conformers have been formed or not.
β-methyl styrene
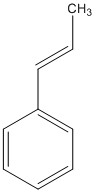
| Transition State Set | (R,R) | (S,S) |
|---|---|---|
| 1 | -1343.022970 !! | -1343.017942 |
| 2 | -1343.019233 | -1343.017942 |
| 3 | -1343.02972 | -1343.023766 |
| 4 | -1343.032443 | -1343.024742 |
The lowest energy transition states were both found in Transition State Set 4. The difference in energy in Jmol-1 is 20,218.98 to give the equilibrium constant K of 2.868 using the following formula.
Furthermore, this K (indicating the ratio of the two isomers) can be used to work out the enantiomeric excess as 99.94%.
Literature gives the value of ee as 90% [25]which does show the enantiomer is very preferred; the decrease in enantiomeric excess may be due to different concentrations, temperatures and byproducts that cannot be easily replicated in computer modelling. It could be argued that computer modelling is more reliable because it can ignore any of these effects.
Non-Covalent Interactions in the Active Site of the Reaction Transition State
Orbital |
For the NCI analysis, the lowest energy transition state of the dihydronaphthalene reacting with Jacobsen's catalyst was used. The energies were compared using the log files provided and it was determined that Set 1 of (S,R) was the lowest in energy. Therefore, a prediction was made that the forces observed would be mostly attractive with minimal repulsive forces. To test this hypothesis, an NCI analysis could have been carried out on the highest energy transition state.
The NCI surface above does support the idea of there being lots of attractive forces (where blue indicates attractive and green mildly attractive) and only very small amounts of repulsive forces (where red indicates repulsive and yellow indicates mildly repulsive). There was attraction between the methyl groups of tertiary butyl groups, which most likely assisted in the lowering of the transition state. Also, attractive forces can be seen between a nitrogen on the Jacobsen's catalyst and one of the carbons on the alkene. In this transition state, no double bond is seen and the hydrogens are not yet in the correct orientation (pointing away from the catalyst) but the oxygen is aligned in a position appropriate to form the epoxide. There is further mild attractive forces between the cyclohexene ring of the dihydronaphthalane and one of the rings containing tertiary butyl groups on the Jacobsen's catalyst.
Electronic Topology (QTAIM) in the Active Site of the Reaction Transition State
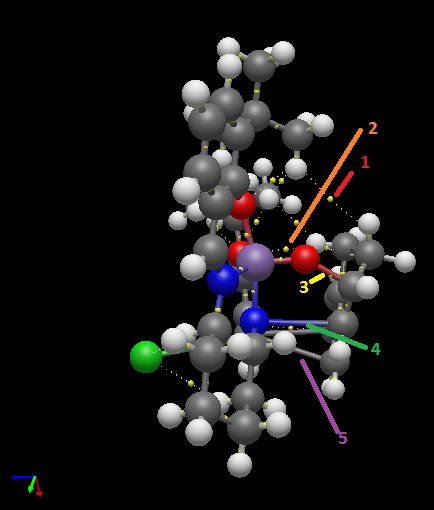
1) Weak non-covalent BCPs between the protons of the tertiary butyl groups on the Jacobsen's catalyst and the protons on the ring that contains the double bond.
2) There are also weak non-covalent BCPs between the protons on the ring and an oxygen bound to the metal centre that is not the oxygen transferred in the epoxidation reaction.
3) There is a covalent BCP between the oxygen to be transferred and carbon of the double bond that will form the epoxide, indicating the start of the epoxidation reaction.
4) There is another covalent BCP between the nitrogen of the catalyst and the other carbon of the double bond that will form the epoxide. This indicates that the nitrogen could be used to facilitate the approach of the alkene and further stabilise the transition state but is less easily broken that the Mn-O bond so does not form an azidirine as it is also stabilised by the rings.
5) There are two covalent BCPs between the carbons of the cyclohexene ring in the approaching alkene and a carbon in a ring on the catalyst, matching the favourable interactions seen in the NCI analysis above.
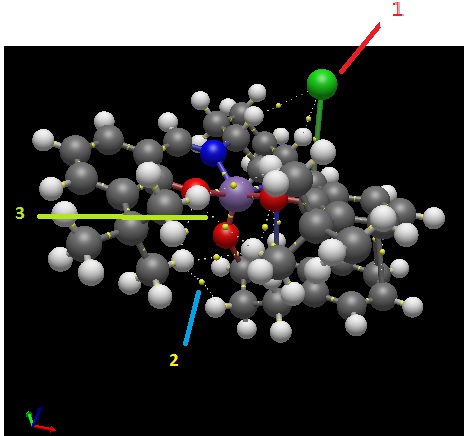
1) Weak non-covalent BCPs are between the Hs on cyclohexene ring bound to Cl, supporting the attractive forces seen in the NCI analysis.
2) There are also weak non-covalent BCPs between the protons of the tertiary butyl group, again supporting the NCI surface analysis.
3) There are also weak non-covalent BCPs between the oxygen and hydrogens of the tertiary butyl groups.
This data complements the NCI analysis in the previous section to explain why this transition state set is of the lowest energy. If more time were available, it would be interesting to compare this to the QTAIM of the transition state with the highest energy.
Suggested epoxide
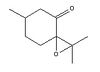
cis R-(+)-pulegone oxide
References
- ↑ T. A. Halgren, J. Comp. Chem., 1996, 17, 490-519.DOI:<490::AID-JCC1>3.0.CO;2-P 10.1002/(SICI)1096-987X(199604)17:5/6<490::AID-JCC1>3.0.CO;2-P
- ↑ P. Caramella, P. Quadrelli, and L. Toma, J. Am. Chem. Soc., 2002, 124, 1130-1131.DOI:10.1021/ja016622h
- ↑ D. Skala, J. Hanika, Petroleum and Coal, 2003, 45, 105-108.
- ↑ IUPAC, 2nd Ed., A. D. McNaught and A. Wilkinson, Blackwell Scientific Publications, Oxford, 1997, DOI:10.1351/goldbook
- ↑ K. C. Nicolaou, Z. Yang, J. J. Liu, H. Ueno, P. G. Nantermet, R. K. Guy, C. F. Claiborne, J. Renaud, E. A. Couladouros, K. Paulvannan & E. J. Sorensen, Nature, 1994, 367, 630-634.DOI:10.1038/367630a0
- ↑ 6.0 6.1 Daisy Archer, DOI:10042/27399
- ↑ 7.0 7.1 Spectroscopic data: L. Paquette, N. A. Pegg, D. Toops, G. D. Maynard, R. D. Rogers, J. Am. Chem. Soc.,, 1990, 112, 277-283. DOI:10.1021/ja00157a043
- ↑ Daisy Archer. DOI:10042/27400
- ↑ A. Burke , P. Dillon , Kyle Martin and T. W. Hanks, J. Chem. Educ., 2000, 77, 271; DOI:10.1021/ed077p271
- ↑ G. A. Jeffrey, J. A. Pople, L. Radom, Carbohyd. Res., 1972,25, 117-131.
- ↑ J. Hanson,J. Chem. Educ., 2001, 78, 1266; DOI:10.1021/ed078p1266
- ↑ Daisy ArcherDOI:10042/27397
- ↑ 13.0 13.1 K. Smith, C-H Liu, G. A. El-Hiti,Org. Biomol. Chem., 2006, 4, 917-927; DOI:10.1039/B517611P
- ↑ Daisy Archer. DOI:10042/27401
- ↑ Daisy Archer. DOI:10042/27393
- ↑ H. Lin, Y. Liu, J. Qiao, Z-L Wu, H. Lin, J. Qiao, J. Mol. Cat., 2010, 67, 236-241.
- ↑ Archelas, Furstoss, Pedragosa-Moreau, Tetrahedron, '1996', 52, 4593-4606.
- ↑ 18.0 18.1 Daisy Archer. DOI:10042/27396
- ↑ 19.0 19.1 Daisy Archer. DOI:10042/27395
- ↑ 20.0 20.1 D. J. Phillips, J. L. Kean, A. E. Graham,Tetrahedron, 2013, 69, 6196-6202; DOI:10.1039/B517611P
- ↑ Daisy Archer. DOI:10042/27398
- ↑ E. J. Corey, P. B. Hopkins, Tetrahedron, 1982, 23, 1979-1982.
- ↑ Daisy Archer. DOI:10042/27392
- ↑ V. Calo, L. Lopez, V. Fiandanese, F. Naso, L. Ronzini, Tetrahedron, 1978, 49, 4963-4966.
- ↑ O. A. Wong, B. Wang, M-X Zhao, Y. Shi, J. Org. Chem., 2009, 74, 6335–6338.DOI:10.1021/jo900739q