Module 3

Optimizing the Reactants and Products

Result

Name	Structure	Symmetry	Energy/Hartrees	Energy/kcal/mol	ΔE/kcal/mol
Gauche 1		C₂/C₁	-231.68771612	-145386.127	3.103
Gauche 2		C₂/C₁	-231.69166701	-145388.606	0.624
Gauche 3		C₁	-231.69266120	-145389.230	0.000
Gauche 4		C₂/C₁	-231.69130310	-145388.378	0.852
Gauche 5		C₁	-231.68961574	-145387.319	1.911
Gauche 6		C₁	-231.68916016	-145387.033	2.197
Anti 1		C₂/C₁	-231.69260235	-145389.193	0.037
Anti 2		C_i/C₁	-231.69253524	-145389.151	0.079
Anti 3		C_2H/C₁	-231.68907065	-145386.977	2.253
Anti 4		C₁	-231.69097054	-145388.169	1.061
Anti 5		C_2H/C₁	-231.68539601	-145384.671	4.559

1 hartree = 627.509 kcal/mol

Discussion

From the argument of geometry, the energies should be lower for the anti arrangement, this is because of less steric intramolecular interactions which can increase strain and thus increasing the energy of the conformer. But as can be seen from the ΔE that this is not the case for the method used, so either there is some stereo electronic interaction (gauche effect), which is stabilizing the C=C double bond, or the method used is not accurate enough to take this into account.

On comparison to the appendix, the energies are very similar showing success in the calculation.

A further look into better approximations could be done to prove this assumption.

These energies below were calculated using Hartree fock method using B-31G basis set.

Conformer	Symmetry	Energy/Hartrees	Energy/kcal/mol	ΔE/kcal/mol
anti:1	C2/C1	-232.89555613	-146144.058	0.000
anti:2	Ci/C1	-232.89548173	-146144.011	0.047
anti:3	C2H/C1	-232.89250529	-146142.143	1.914
anti:4	C1	-232.89412102	-146143.157	0.901
anti:5	C2H/C1	-232.88899212	-146139.939	4.119
gauche:1	C2/C1	-232.89063389	-146140.969	3.089
gauche:2	C2/C1	-232.89459175	-146143.452	0.605
gauche:3	C1	-232.88794105	-146139.279	4.779
gauche:4	C2/C1	-232.89413793	-146143.168	0.890
gauche:5	C1	-232.89241728	-146142.088	1.970
gauche:6	C1	-232.89206639	-146141.868	2.190

Now It can be clearly seen that the energies are lower for the Anti conformer. Thus the 3-21G basis set must leave out or not have a strong enough force constant for steric intramolecular interactions.

Anti2

Geometry

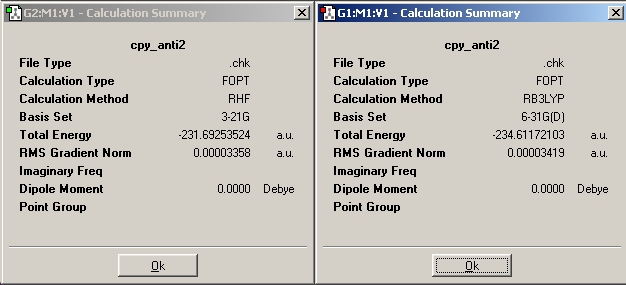
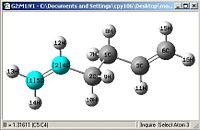
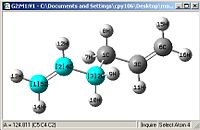
A comparison of optimisations using HF/3-21G and a further optimisation using DFT-B3LYP/6-31G(D).


Bond length= 1.316Å	Bond length= 1.553Å	Angle= 124.81^o	Angle= 111.34^o

Bond length= 1.334Å	Bond length= 1.548Å	Angle= 125.31^o	Angle= 112.69^o

HF/3-21G

DFT-B3LYP/6-31G(D)

From first glace the structures look pretty much identical, but a closer examination shows otherwise. Most of the bond lengths and angles were slightly out by a couple of degrees or 0.01Å which accumulate to create a greater difference in the energies obtained as well

One other thing which was noticed was that the C=C double bond is considerably longer and the bond angle is more angled, this shows that the HF/3-21G method shows a more accurate force constant for π C=C double bonds.

Imaginary Frequencies

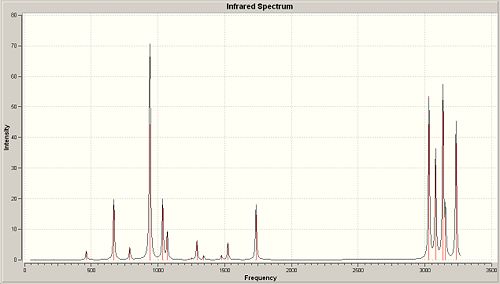
As can be seen from the spectra above, there are no negative (or imaginary) frequencies present and thus shows that this is the lowest energy conformer.

Energies

Sum of electronic and zero-point Energies=           -234.469187 a.u.
Sum of electronic and thermal Energies=              -234.461837 a.u.
Sum of electronic and thermal Enthalpies=            -234.460893 a.u.
Sum of electronic and thermal Free Energies=         -234.500778 a.u.

By using these separate energies and the total energy, since energy is made up from many different components then such as electronic, vibrational, rotational and translational subtracting each component can give you specific values of each of these components.

Notes

The table was set out for easy comparison.

Optimizing the "Chair" and "Boat" Transition Structures

unless stated all operations were done using hartree-fock method with a 3-21G basis set.

Creating Transition States:


Bond length= 2.020Å	Bond length= 1.389Å	Angle= 120.49^o	Angle= 101.87^o

Bond length= 2.021Å	Bond length= 1.389Å	Angle= 120.49^o	Angle= 101.85^o

Both the guess method with TS (Berny) optimisation and Freezing coordinates method both produce very similar results as they do both use the same optimisation method, but the only difference would be, that in a case where the guess (for the guess method) was not sufficiently close enough to the transition state structure, that it would give an incorrect answer. Freezing the bonds and drawing it via this method, takes slightly longer but is more likely to succeed in obtaining the correct transition state structure.

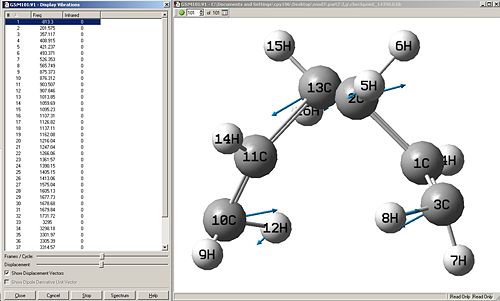
Both of these structures produced negative imaginary frequencies (-818.112, -817.759) which shows that it is not the lowest energy conformer.

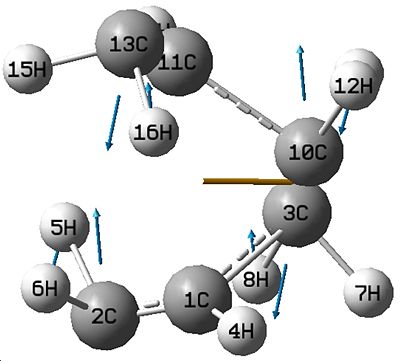
This vibration shown is Asymmetric, which is correct because it shows that one bond is breaking while the other is forming.

QST2-Boat

Reactant, Product:

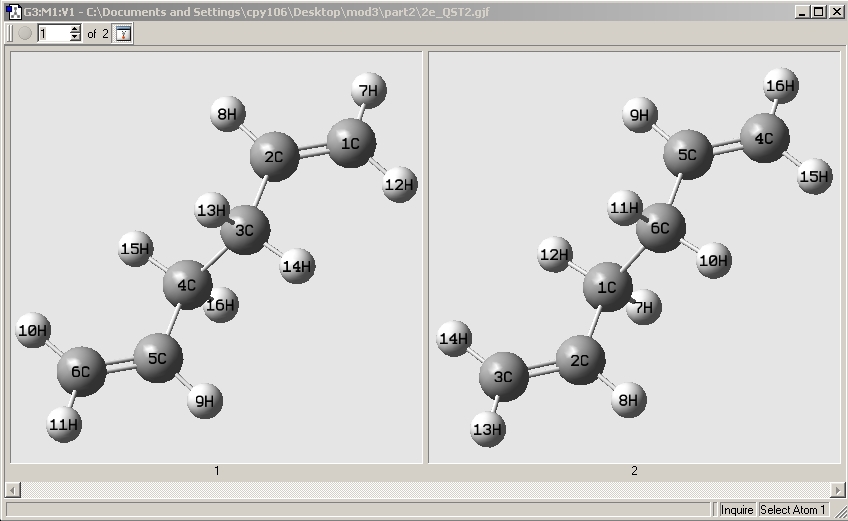
1 denotes the reactant and 2 denotes the product.

Failed Attempt:

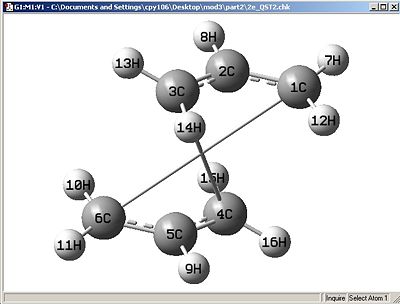
This attempt failed as the operation failed to re-orientate the molecule effectively to give the correct geometry and thus not giving the correct transition state.

Succeeded Attempt:

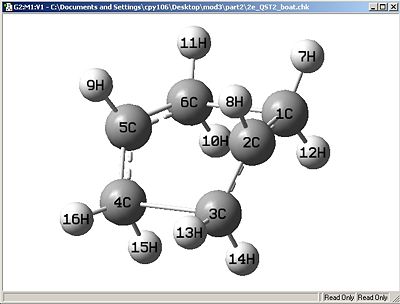
After rotating a few bonds to give a more true representation, the QST2 operation was able to succeed to give the transition state. The vibrational spectra showed a imaginary frequency at -839.407 (negative values constitute to transition state structures).

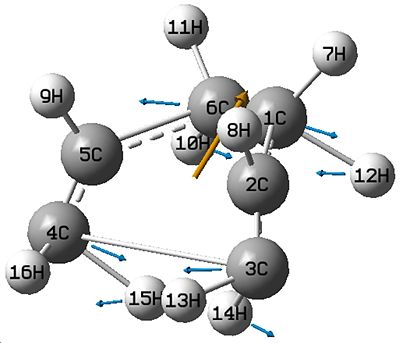
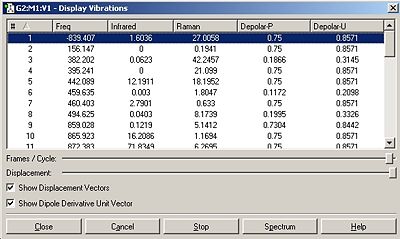
This Asymmetric stretch shows bond breaking and formation.

Conformers of 1,5-hexadiene correlate well with the structures of the boat and chair conformers, would be the gauche conformers, as they look like they are closer to the transition state.

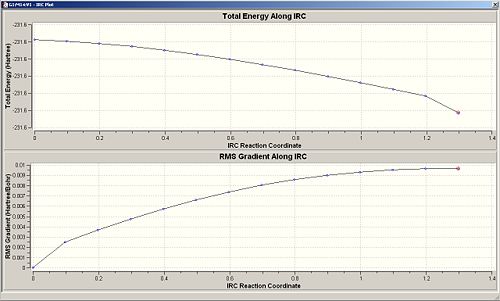
Intrinsic Reaction Coordinate

Force const:once Number of Points:50

Force const:once Number of Points:100

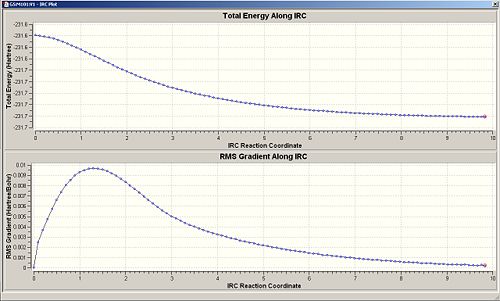
Force const:always Number of Points:50

Force const:always Number of Points:100

Discussion

When the calculation for the force constant is set to once, then the change in energy is very gradual, but as shown in the first computed results, it can be seen that even 50 points were not enough to obtain a minimum. The same method with force constant=once was ran again but with 100 points, this gives the second set of computed results, this is much better as the energy curve levels off to almost flat, this shows that an energy minima can be reached when introducing more points, which is good.

The next logical step would be to change the force constant to always calculate, from initial thoughts, this method might take longer in the sense that a force constant has to be calculated each step of the way, but possibly faster due to more accurate changes. It turns out that the method using always seemed to decrease in energy too quickly for the number of points=5, so another trial was done with 100 points, but this had no effect, the energies still did not converge to a horizontal line, but the energy against reaction coordinate plot shows that a minima has definiently not been reached.

Thus concluding from this, calculating the force constant always, is quite a lengthy process and is not worth waiting for, as well as it some times doesn't even converge, and that calculating the force constant once needs an increased amount of points to reach an energy minima. For this molecule (and its molecular complexity), calculating force constant=once and the number of points=100, is the best method to use in this situation.

Activation Energy

From using all the previously obtained data, it is possible to find a calculated activation energy, using the reactants and the transition state.

These energies were calculated using the Hartree-fock method using a 3-21G basis set.

Conformer	Energy/Hartrees	Energy/kcal/mol	ΔE/kcal/mol
Reactants (Electronic)	-231.692535	-145389.151
Reactants (0K)	-231.539541	-145293.146
Reactants (298.15K)	-231.532567	-145288.770
Chair TS (Electronic)	-231.619322	-145343.209	45.94
Chair TS (0K)	-231.466701	-145247.438	45.71
Chair TS (298.15K)	-231.461341	-145244.075	44.69
Boat TS (Electronic)	-231.602802	-145332.843	56.31
Boat TS (0K)	-231.450939	-145237.547	55.60
Boat TS (298.15K)	-231.445314	-145234.018	54.75

These energies were calculated using the DFT-B3LYP method using a 6-31G basis set.

Conformer	Energy/Hartrees	Energy/kcal/mol	ΔE/kcal/mol
Reactants (Electronic)	-234.611718	-147220.965
Reactants (0K)	-234.469187	-147131.525
Reactants (298.15K)	-234.461837	-147126.913
Chair TS (Electronic)	-234.556983	-147186.618	34.35
Chair TS (0K)	-234.414930	-147097.478	34.05
Chair TS (298.15K)	-234.409009	-147093.763	33.15
Boat TS (Electronic)	-234.543092	-147177.901	43.06
Boat TS (0K)	-234.402359	-147089.590	41.94
Boat TS (298.15K)	-234.396025	-147085.615	41.30

Literature data at 0K

chair transition structure	33.5 ± 0.5 kcal/mol
boat transition structure	44.7 ± 2.0 kcal/mol

Discussion

From comparing the literature with the computed data, it clearly shows that the DFT-B3LYP/6-31G method gives far more realistic and accurate data than the HF/3-21G. The energies for the chair structure are almost identical but this can be expected as the symmetry is higher and thus easier to predict. For the boat conformer the energy which is predicted by the DFT-B3LYP/6-31G method is slightly lower this could have been due to the incorrect geometry predicted when doing the optimisation. Overall the DFT-B3LYP/6-31G method produces realistic activation energies for the boat and chair structures.

The Diels Alder Cycloaddition

Cisbutadiene


Homo - Antisymetric	Lumo - Symetric

Guessing the transition structure

In this part the same method of freezing bond lengths was used to obtain a more true transition structure

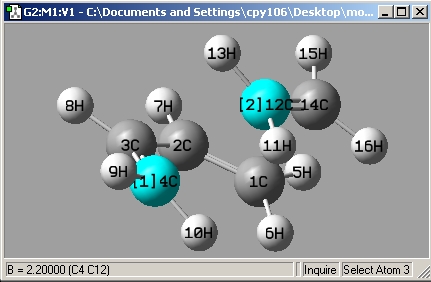
The forming bonds would be set to a distance of 2.2Å then reoptimised using ts(berny) and bond derivatives.

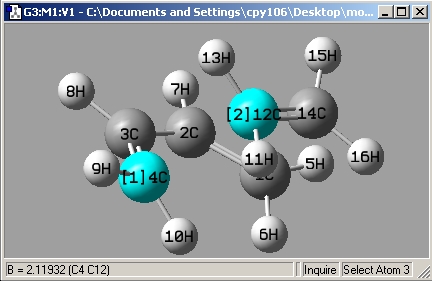
bond length = 2.12Å. typical C-C bond lengths are approximately ~ 1.5Å give or take 0.05Å due to different hybridization (more or less S character). but it is clear that 2.12Å is too long to be a normal C-C bond length.

A vibrational analysis was taken of the molecule to determine whether it had any imaginary frequencies, and thus if it was a transition state structure.

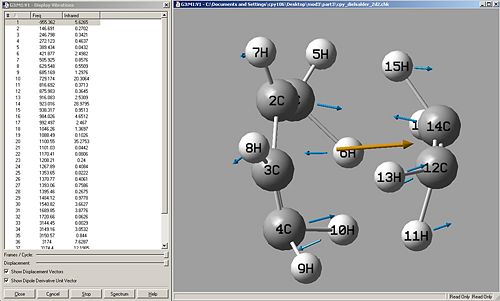
Imaginary Frequency = -955.362

This shows it is a transition state structure, and the vibration clearly shows the mechanism of reaction. Carbon4 bonds with carbon12 and carbon1 (behind carbon2) bonds with carbon14, this vibration take place synchronous.The next frequency along shows a twist of the ethene on the cisbutadiene with an asynchronous fashion.


Homo - asymetric	Lumo - symetric

Formation of transition state homo

The transition structure's homo is made up of the homo from the cisbutadiene and the lumo of the ethene


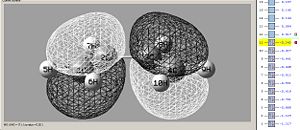
Ethene Lumo - asymmetric	Cisbutadiene Homo - asymmetric	Transition structure Homo - asymmetric

This reaction takes place due to good overlap density of the orbitals, electrons from the homo of the cisbutadiene going into the lumo of the ethene, the correct phases of the orbitals means that the interaction is constructive, and doesn't cancel out.

Cyclohexa-1,3-diene reaction with Maleic anhydride

The optimisations of the structures were done in much the same way as the previous section (e.g. guess structure, freeze bond, optimise, bond derivative, then re-optimise).

Firstly maleic anhydride and cyclohexadiene were drawn then optimised

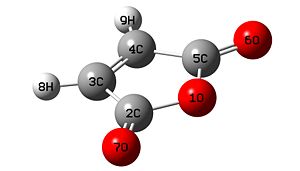
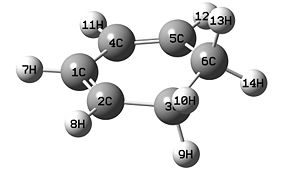
Freezing Bonds to 2.2Å then optimising:


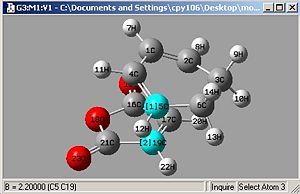
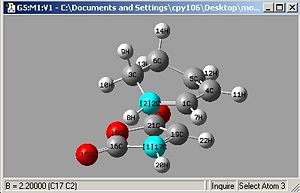
Endo	Exo

bond lengths set to 2.2Å

Then Taking the Bond derivative:


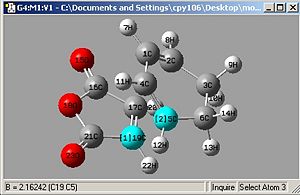
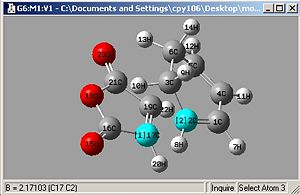
Endo: Bond Length=2.162Å	Exo: Bond Length=2.171Å

It's clear that the Endo bond length is shorter, and this can be explained by looking at the molecular orbitals. Exo and Endo are isomers, Exo is where the electron withdrawing groups on the dieneophile are pointing away from the diene and endo is where they are both pointing in the same direction.

Vibrational Frequencies


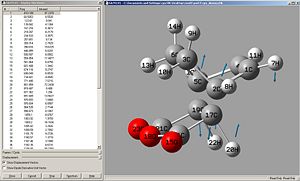
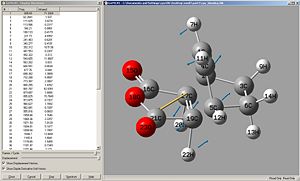
Exo	Endo

Again, the negative frequencies show that this is the transition state structure. the vibrations correspond to the bond forming/breaking and this happens synchronously.

Molecular Orbitals

Maleic anhydride:


Maleic anhydride Lumo - asymetric	Maleic anhydride Homo - symetric

Cyclohexandiene:


Cyclohexadiene Lumo - symetric	Cyclohexadiene Homo - asymetric

Exo:


Lumo - asymetric	Homo - asymetric

This Exo structure shows strain from the steric de-stablising effects from the CH₂ groups, these are directly above the oxygen atoms, but as can be seen from the homo that there is no stabilsing effect from the orbital overlap, therefore the CH₂ groups may be repelled away causing strain.

Endo:


Lumo - asymetric	Homo - asymetric

In this Endo molecular orbital the bonding lobes have a larger overlap, this means that the bond strength is increased and that the bond length is decreased.

Energies

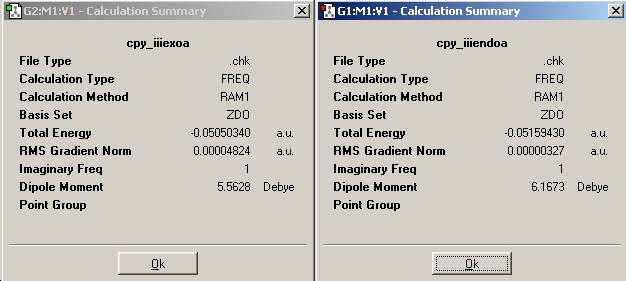
From looking at the relative energies, the endo seems to be lower in energy, this could be due to increase overlap of the molecular orbitals.

secondary orbital overlap effect is where the carbonyls overlap with the transition state orbitals on the diene stabilising/favoring the endo structure (from stabilising the transition state).

A more accurate optimisation using the DFT-B3LYP/6-31G(d) was done for the exo and endo structure to be sure of the relative energies.

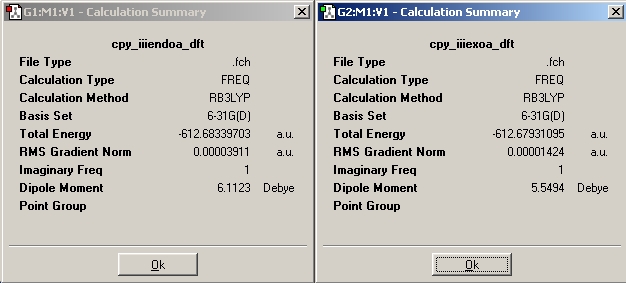
After running the energies the endo is still the lower energy conformer.

Conclusion

Overall this experiment shows that by computational means it is possible to calculate transition state structures, activation energies with a high degree of accuracy. This activation energy may be useful in finding new methods (conditions) or mechanisms to reactions. With out further examination, i cannot suggest any improvements. But this experiment is a very powerful method for predicting physical data.

General Notes

All frequencies are given in wave numbers (cm^-1) unless stated otherwise. All energies are given in Hartrees (a.u.) unless otherwise stated. Basic starting structures were obtained using chembio3d and then saving as a gaussian input file. All calculations in "Cyclohexa-1,3-diene reaction with Maleic anhydride" were done using a semi empirical AM1 method, unless stated otherwise. TS=transition state