Rep:Mod:gnapqwsazx

Inorganic Computational

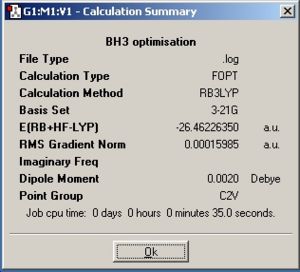
BH₃

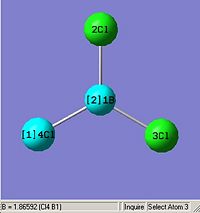
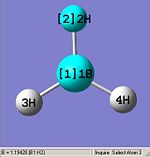
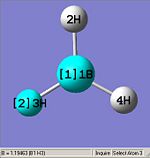
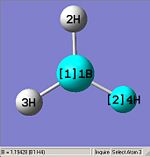
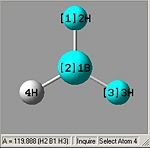
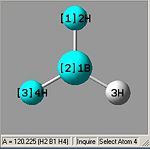
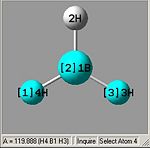
From optimising BH3, with a method (DFT)B3LYP and a basis set of 3-21G, the values obtained for the bond lengths were 1.19428, 1.19463 and 1.19428A. The Bond angles obtained were 119.888, 120.225 and 119.888 deg all in a planar arrangement.

Ideally all angles and bond lengths should have turned out to be equivalent, but due to the "poor" approximation using the 3-21G basis set, the accuracy involved is not sufficient in producing such realistic data.

Summary

File type = .log Calculation type = FOPT Calculation method = RB3LYP Basis set = 3-21G Final energy = -26.46226350 a.u. Gradient = 0.00015985 a.u. Dipole moment = 0.0020 Debye Point group = C2V Calculation time = 35.0 seconds

To explain this summery, the basis set used was 3-21G which is a low accuracy calculation, this in turn explains why the calculation time is so short and since the molecule is not fully optimised, the observed dipole moment is 0.0020 Debye instead of 0, with this in mind the uneven bond angles and lengths means that this method was also unable to correctly analyse the point group.

As can be seen, the Z axis from the Cartesian axis should be going through perpendicular to the plane of the molecule (X axis) but GaussView has not recognized this.

This molecule should contain all equal bond lengths and bond angles. Thus giving a D_3h point group

BCl₃

From optimisation using method of (DFT)B3LYP, basis set of LanL2MB and restricting the point group to D_3h constrained to 0.0001 tolerance. The values obtained from the bond length is 1.87A and 120.00 deg for the bond angle, these values were consistent in all bonds and all angles.

File type = .log Calculation type = FOPT Calculation method = RB3LYP Basis set = LanL2MB Final energy = -69.4393 (±0.00038088) a.u. Gradient = 0.00005905 a.u. Dipole moment = 0.00 Debye Point group = D3h Calculation time = 12.0 seconds

Errors

Since 1 a.u. = 2625.5 kj/mol and the energy will have an error of 1 kj/mol = 0.00038088 a.u. All other errors have been corrected in the table above.

H₂O

Standard orientation: --------------------------------------------------------------------- Center Atomic Atomic Coordinates (Angstroms) Number Number Type X Y Z --------------------------------------------------------------------- 1 8 0 0.000000 0.000000 0.122755 2 1 0 0.000000 0.785462 -0.491020 3 1 0 0.000000 -0.785462 -0.491020 ---------------------------------------------------------------------

File type = .log Calculation type = FOPT Calculation method = RB3LYP Basis set = 3-21G Final energy = -75.974 (±0.00038088) a.u. Gradient = 0.00011752 a.u. Dipole moment = 2.24 Debye Point group = D2v Calculation time = 16.0 seconds

---

Log file of Water

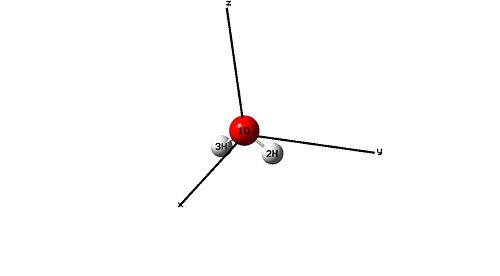
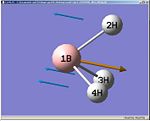
BH₃ Vibrational Frequencies

Vibration
No	1	2	3	4	5	6
Frequency/cm^-1	1146	1203	1206	2593	2730	2732
Intensity	92(.7)	12(.3883)	12(.3759)	0(.0069)	104(.053)	103(.616)
Point Group D3h symmetry	A"2	E'	E'	A'	E'	E'
Explanations	Hydrogen atoms moving parallel to the Z C3 axis	Movement of hydrogen's 2 and 4 around the boron center	Movement of all hydrogen atoms around the boron center	Movement of all the hydrogen's along the bond in/out from the boron center	Movement of all of 2 hydrogen's to the boron center and one moving away	Stretch of 2 hydrogen atoms towards the boron center

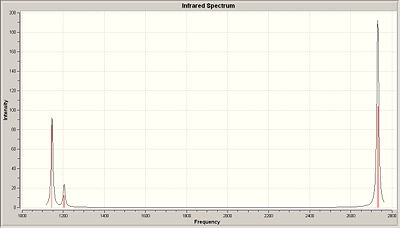
Notes: since the point group was C_2v to start off with, the energies are not quite degenerate(as would be found for a D_3h system. All the point groups were assigned to a D_3h point group and not the incorrect C_2v. Decimal places were left in to show this point group error.

BH₃ Molecular Orbital

Mo along the Z axis
Mo along the X axis
Orbital	homo-2	homo-1	homo	homo	lumo	lumo+1	lumo+1	lumo+2
Relative Energies	-6.730	-0.517	-0.357	-0.356	-0.074	0.188	0.189	0.191
Symmetry		a'1	e'	e'	a"	a'	e'

• The 2 molecular orbitals which say homo are both degenerate, in this case the energies are very slightly different due to the incorrect C_2v symetry label as is the same for lumo+1.

All solid black circles show empty spaces (thus only looking at the high lighted atom's orbitals).

Comments

From looking at the linear combination of atomic orbitals and comparing with the generated molecular orbitals by using computational methods, it can be seen that the resemblance is quite similar for most, the only case which it may appear hard to see is the lumo+1 where the black coloured orbitals are pushed out to the side. As there is no suitable reference for the energies no further comments can be made from the relative energies of the computational method, only that the order of which the orbitals come are in the correct order.

Mo(PMe3)2(CO)-Trans and Cis

Geometry

Cis

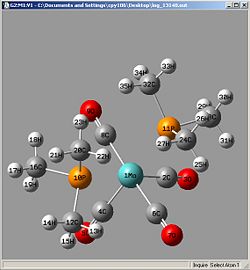
Bond	Length/A	Lit
1Mo-2C	1.99489	1.975
1Mo-4C	1.99206	1.966
1Mo-6C	2.03184	2.022
1Mo-8C	2.03187	2.042
1Mo-10P	2.58804	2.522
1Mo-11P	2.59372	2.522
2C-3O	1.18982	1.142
4C-5O	1.19115	1.144
6C-7O	1.18799	1.140
8C-9O	1.18799	1.125

Trans

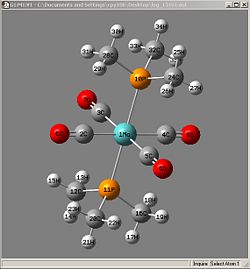
Bond	Length/A	Lit
1Mo-2C	2.02994	2.016
1Mo-3C	2.02990	2.005
1Mo-4C	2.02988	2.016
1Mo-5C	2.02995	2.005
1Mo-10P	2.52513	2.500
1Mo-11P	2.52508	2.500
2C-6O	1.18918	1.164
3C-7O	1.18916	1.165
4C-8O	1.18917	1.164
5C-9O	1.18917	1.165

Angles 10P-1Mo-11P

	Angle between trans isomer	Angle between cis isomer
Computed	179.959	96.709
Lit	180.00	97.54

Optimisations were done with B3LYP/LANL2MB then B3LYP/LANL2DZ and then the more advanced calculations taking into about Phosphorous' hyper valency and occupation of low lying d orbitals. The calculated values correspond very well to literature, particularly the P-Mo-P bond angle for cis. This shows that high level calculation can product highly realistic results.

Vibrations

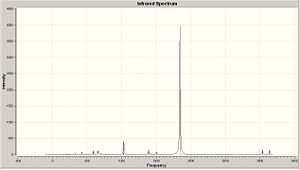
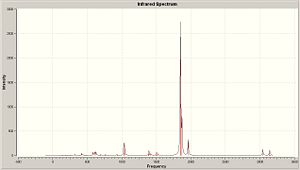
Trans Spectra	Cis Spectra

Trans	1843, 2008	1843, 2012	1886, 0	1959, 0
Trans Lit	1896	1896
Cis	1850, 1966	1854, 1063	1874, 678	1962, 329
Cis Lit	1886.7	1898.5	1913.7	2012.4

key:(frequencies, intensity)

From a direct comparison to the literature values, it can be seen, even though the phosphine ligands are slightly different, that values correspond very well with the degree of accuracy used. Not only this but with reference to the graphs seen in the literature the intensities are also realistic to data. So this shows that optimisation with B3LYP method and LANL2DZ pseudo-potential basis set, then further advanced optimasation (incorporating hyper valency and use of low lying d orbitals), gives a good approximation to the C=O stretching frequencies.

---

1. Cis Optimised DOI:10042/to-1954
2. Trans Optimised DOI:10042/to-1955
3. Cis Frequency DOI:10042/to-1956
4. Trans Frequency DOI:10042/to-1957
5. Geometry of Trans isomer: G. Hogarth and T. Norman, Inorganica Chimica Acta, 1997, 254, 167-171 DOI:10.1016/S0020-1693(96)05133-X
6. IR data of Trans isomer: D. J. Darensbourg and R. L. Kump, Inorg. Chem., 1978, 17, 2680-2682 DOI:10.1021/ic50187a062
7. Geometry of Cis isomer: F. A. Cotton, D. J. Darensbourg, S. Klein and B. W. S. Kolthammer, Inorg. Chem., 1982, 21, 2661-2666 DOI:10.1021/ic00137a026
8. IR data of Cis isomer: A. D. Allen. and P. F. Barrett, Can. J. Chem., 1968, 46, 1649–1653 DOI:10.1139/v68-276

NH₃

Symmetry

Summary windows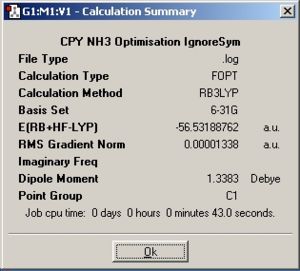
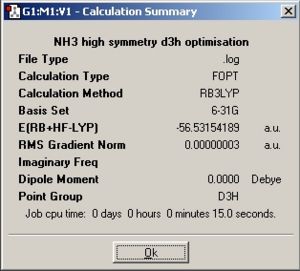
Point group	C1	C3v	D3h
Jmol	Pentahelicene	Pentahelicene	Pentahelicene

The symmetry changes the structure of the molecule, if the symmetry is set, then the requirements of that symmetry operation must be met. Hence if C₁ then all the bond lengths and angles cannot be equal, otherwise this would produce C_3v so the symmetry has made a difference to the optimised geometry. This can also be seen in D_3h where the molecule is now planar to satisfy the D_3h operation.

A molecule cannot break symmetry when performing an optimisation. The molecule is most likely to stay with the same symmetry (as some symmetry requirements may require the geometry to be at a very high precision before accepting a different symmetry point group. Therefore if a high symmetry structure is optimised this molecule will already have to have the correct symmetry or it will have to be set manually. The NH₃ with C₁ contained the lowest energy then C_3v and then D_3h. This is due to increased stabilisation from orbital mixing due to Jahn Teller effect (increased orbital mixing due to vibrations (or decrease in symmetry) which increases orbital overlap, stabilising molecules). This would show why C₁ took the longest as well due to its lower symmetry.

Point Group	Energy/a.u.	Energy/kJ/mol	ΔEnergy/kJ/mol
C1	-56.53188762	-148424.4709	0
C3v	-56.5318859	-148424.4664	0.00451586
D3h	-56.53154189	-148423.5632	0.907714115

Method

Summary windows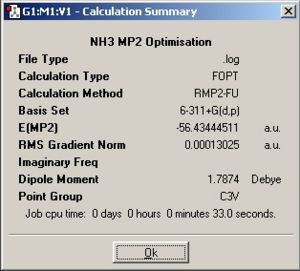
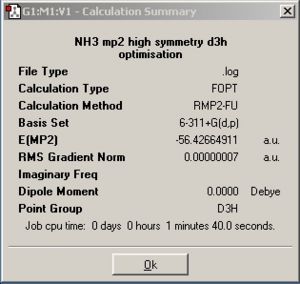
Point group	C3v	D3h

Point Group	Energy/a.u.	Energy/kJ/mol	ΔEnergy/kJ/mol
C3v	-56.43444511	-148168.6356	0
D3h	-56.42664911	-148148.1672	20.468398

In this section the optimisations are done with a more accurate MP2 method and a more accurate basis set to gain more a realistic models. The time taken for the C_3v was similar to the lower level calculation but the D_3h symmetry model takes more time. The energy difference is 20.47kJ/mol which compared to 0.9077kJ/mol, from using the lower level calculation, is a lot higher, but when compared to the experimental value of 24.3 kJ/mol it is clear that the MP2 calculation is a lot more realistic.

Vibration

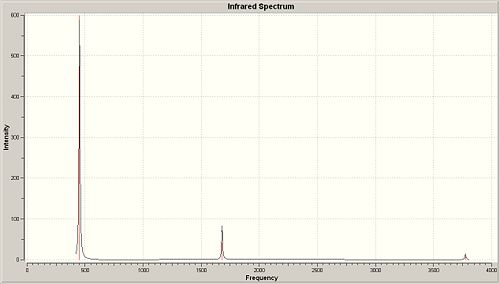
• C_3v

Number	1	2	3	4	5	6
Frequency	452.3016	1680.4675	1680.4677	3575.4284	3775.7592	3775.7593
Intensity	599.4721	41.7256	41.7245	0.0688	7.0892	7.0884
Symmetry group	A	E	E	A	E	E

• D_3h

Number	1	2	3	4	5	6
Frequency	-318.0512	1640.5919	1640.5927	3635.7096	3854.2691	3854.2693
Intensity	849.1132	55.9828	55.9805	0.0000	19.5951	19.5963
Symmetry group	A"	E'	E'	A'	E'	E'

In C_3v all of the frequencies are positive but in D_3h all but one is positive. The vibrations all seem to be the same but from looking at the last 2 degenerate vibrations (5 and 6) it is seen that these are swapped around. The vibration which follows the inversion pathway is vibration 1, the reasoning being is that the stretch actually inverts and passes through a D_3h state back into the inverted C_3v state. The transition state structure gives a frequency of -318.05.

Experimental Literature

Computed Freq	452.3016	1680.4675	1680.4677	3575.4284	3775.7592	3775.7593
Experimental Lit Freq	932/968	1626	1626	3337	3444	3444

From looking at these values , they all seem to have been predicted higher by computational methods, except for the first vibration. The first vibrations is the furthest out, this could be due to the lower basis set calculation used, which previously seen only gave 0.9kJ/mol for the inversion energy. IT also seems that vibration 1 is the one which is most related to the inversion barrier and thus is most effected by the low level calculation basis set.

MiniProject

The mini project will be based on the Nickel complex α-diimine Ligand. This basic molecular outline is used in many reactions for polymerisation reaction. The catalyst has to first be activated using MAO to methylate the Ni(II) metal, and from this can be used in catalytic polymerisation cycles (e.g. oxidative addition, insertion and then reductive elimination). There is already extencive research into this field by using increased sterically bulky groups on the ligand itself.

By computation methods, effects on changing α-diimine ligand can be observed, whether it be in geometry, electronegativity, vibrations or possibly a significant change in the molecular orbital’s. By looking at these changes and analysis of them a better idea of the possible improvements maybe be found as a catalyst for polymerisation (such as increasing the or decreasing charge distribution at the catalytic metal center.

The optimisations where done in 2 stages (B3LYP/LANL2MB then B3LYP/LANL2DZ). Further optimisation with an MP2 method was approached, but results were not obtainable due to the time length of the calculation. Frequencies, molecular orbitals and charge distribution were obtained by changing from optimisation to frequencies, and adding pop=(full,nbo)to the additional commands after the B3LYP/LANL2DZ optimisation.

To begin the optimised geometry of the α-diimine ligand complex will be done.

---

L. K. Johnson, D. Tempel, C. M. Killian, and M. Brookhart. Macromolecules 2001, 34, 362-371 DOI:10.1021/ma0012898

Geometry

	Pentahelicene
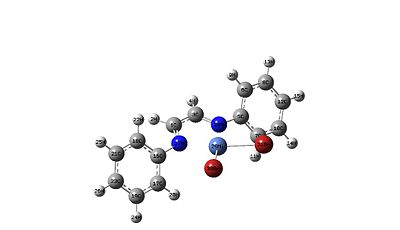
kz(H)(Br)	jmol

As can be seen from the optimisations the complex is planar. This planar arrangement is due to the fact that Ni(II) complexes are d⁸ which prefer to be in a square planar arrangement. how ever the phenyl rings are not planar about the ligand and are not 90^o to the nitrogen atoms of the center chain (which would look like the most sterically favored). This is because there is a compromise between the overlapping P orbitals from the phenyl rings and the conjugated unsaturated chain the the middle. So overall the phenyl rings would prefer to be planar but the sterics prohibits this.

looking at the bulky substituents, initial thoughts would be that the molecule is tetrahedral at the nickel center, but the energy gained from the square planar arrangement must be higher than that of the steric interactions from the phenyls and the bromines.

After looking at kz(hbr), increasing steric bulk around the phenyl rings would increase the the torsion angle between the phenyl and the NCCN center, this alteration has already been shown experimentally. Thus, having a look at whether or not more electronegative substituents might change the geometry and reactivity seems to be the next sensible course of action.

Comparison of benzene kz(hbr) with pentaflourobenzene kz(fbr)

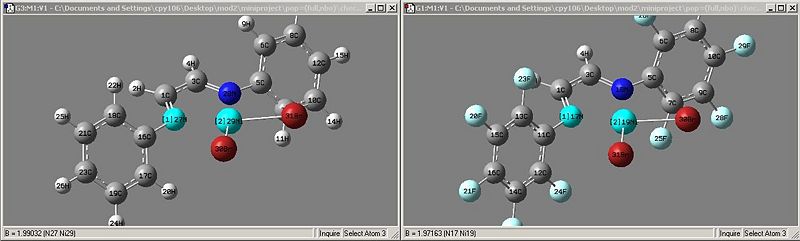
as expected the increase in electron density around the benzene rings is transferred to the nitrogens which then increases the donation from the nitrogen to the nickel center. this is clearly seen in the geometry of the optimised products.

Energies

The energies of the compounds can be seen below

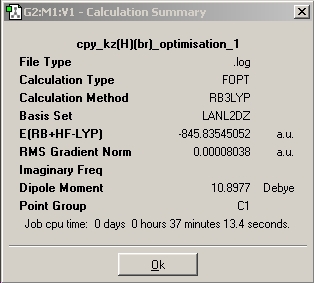
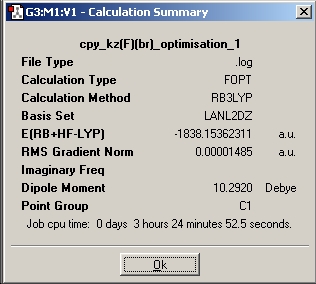
Summary of kz(H)(Br)	Summary of kz(F)(Br)

From looking at the relative energies and it can be seen that kz(F)(Br) is alot lower in energy than kz(H)(Br), this can easily be explained with the help of the C₆H₅-H and C₆H₅-F bond strengths. The bond strength for C₆H₅-F (124kcal/mol) is alot higher than that of C₆H₅-H (110kcal/mol), this gives rise to increase stability and a lower over all energy.

---

Bond strengths of benzene: Gustavo E. Davico, Veronica M. Bierbaum,t Charles H. DePuy,J G. Barney Ellison,J and Robert R. Squires, Am. Chem. SOC. 1995,117, 2590-2599 DOI:10.1021/ja00114a023

Symmetry

The symmetry of this molecule is C₁. This symmetry is expected from a quite complex molecule like this one.

Molecular Orbital

kz(hbr)
kz(fbr)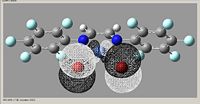
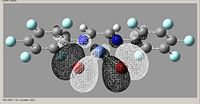
Orbital	Homo-1	Homo	Lumo	Lumo+1

• all energies are negative for these orbitals

From looking at the molecular orbitals, there is little to no difference in the orbitals when the electronegativity is different. Also analysis of these molecular orbitals would not be greatly advantageous in determining if it will be a good catalyst, as this molecule is not the activated form.

With this in mine a look at the charges might help explain what is changed by using pentaflourobenzene rings.

Charge Distribution

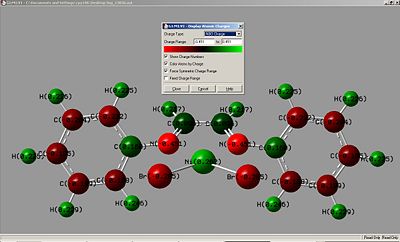
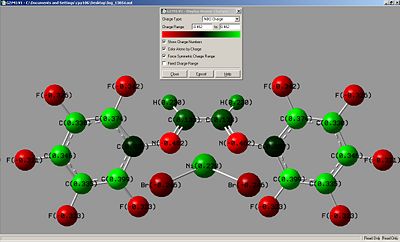
kz(H)(Br)	kz(F)(Br)

As can be seen the charge is reversed around the benzenes on both molecules. By added electronegative groups around the ring the benzene ring the nitrogen shows a more negative charge. The nickel metal center thus has a higher positive charge for kz(F)(Br), This could improve activation or efficiency of the catalyst as the catalyst has to act as an electrophile in polymerisation reactions.

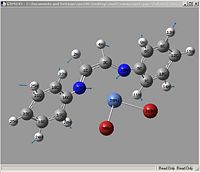
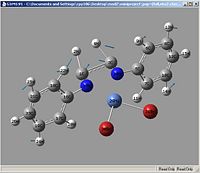
Vibrations

Example Picture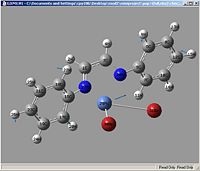
Vibration	Ni-Br	Ni-N	C=N (symetric)	C=N (asymetric)

vibrations	Ni-Br	Ni-N	C=N (symetric)	C=N (asymetric)
kz(H)(Br)	310.362, 10.3696 (16)	857.767, 00.8665 (35)	1530.58, 60.8453 (70)	1600.16, 29.3679 (71)
kz(F)(Br)	339.642, 01.1942 (31)	970.863, 90.4395 (60)	1527.23, 220.997 (80)	1615.37, 09.1841 (81)

Theres are no negative frequencies therefore this structure is at a minimum.

For the kz(H) molecules these have a lot more vibrational stretches than the kz(F), this could be due to the fact that the flourines done participate very well in vibrations around the 500-3000cm^-1 frequency. One explanation could be simply to do with the atomic weight of the fluorine atoms. Another could be due to the fact that since the electron density has been pulled out of the ring there is less electrons to promote, stopping many vibrational frequencies which would have normally been there.

Something else to notice about the values are that the flourine atoms do increase the frequency which means the bond strength is increased in the vibrating molecules.

Lit: 1633cm^-1 (C=N), this value corresponds very closely to that of both the flourinated and benzene α-diimine complex. Even though the literature isnt exactly the same molecule (cyclohexane instead of benzene) a good comparison can be made. This shows that the optimisation method was appropriate for this molecule.

---

Rachel K. O’Reilly, Michael P. Shaver, Vernon C. Gibson, Inorganica Chimica Acta 359 (2006) 4417–4420 DOI:10.1016/j.physletb.2003.10.071

Further Alterations

Since it seemed that changing both sides to the α-diimine ligand had little to no effect on the molecular orbitals, a further investigation into a hypothetical molecule. This would consist of one side flourinated and the other side of the ligand remaining the same. This complex was optimised in much the same way as before.

	kz(HF)(Br)
kz(HF)(Br)	jmol

From compairing the geometries again, the characteristics are dominated by both characteristics of the previous two molecules. One side, the pentaflourinated side, shows a larger toursion angle of 62.8^o with the N=C-C=N center and the benzene side only showing 41.7^o. This large difference can be explained with the reasoning earlier, but this time since flourine atoms are highly electronegative the electron density is less free to be used in conjugation with the N=C-C=N center, or alternatively flourine atoms are alot larger than that of hydrogen and thus just from steric repulsion, the torsion angle is increased.

The next step is to look at the Mo

Molecular Orbital
Orbital	homo-1	homo	lumo	lumo+1

As slightly expected, the molecular orbitals didnt change a great deal, thus the only thing which can really be concluded from this is that the molecular orbitals wont change much in the presence of altered α-diimine ligands.

Conclusion

This experiment was to prove computationally whether or not changing the electronegativity towards a ligand will change any properties. Looking at the geometry and vibrations, it can be seen that increased electronegativity will increase the bond strength (higher frequencies for same/similar vibrations). Bond lengths are significantly effected aswell showing shorter N-Ni bonds which also helps to explain the higher vibrational frequencies and the torsion angle also increases. Computational methods have been compared with literature values (vibrational analysis). Similarities show that using computational methods makes a very good prediction if the correct method and basis sets are applied. Overall the calculations proved to be a success but little information was gathered from the MO's.

Output Files

1. kz(H)(Br) Final Optimised form: DOI:10042/to-1959
2. kz(F)(Br) Final Optimised form: DOI:10042/to-1960
3. kz(H)(Br) Frequency and Mo and NBO: DOI:10042/to-1961
4. kz(F)(Br) Frequency and Mo and NBO: DOI:10042/to-1962
5. kz(HF)(Br) Final Optimised form: DOI:10042/to-1966
6. kz(HF)(Br) Mo: DOI:10042/to-1967

General Notes

All pictures were added for the viewers reference only. All frequencied are quoted in cm^-1 unless stated otherwise.