Rep:Mod:gnapqazwsx

Modelling using Molecular Mechanics

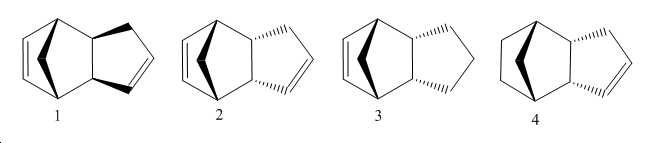
The Hydrogenation of Cyclopentadiene Dimer

Abstract

Chembio3D can be used for many particular jobs such as calculating relative energies, structures, angles etc. In the first part of this module, simple isomer energies are compared to give an idea which of the isomers would be more thermodynamically favorable. The total energy is composed on energies from factors such as stretches bends torsion strain, van der waals interactions within the molecule and so on.

Table of Results

Pentahelicene	Pentahelicene	Pentahelicene	Pentahelicene
(1)exo-product	(2)endo-product	(3)dihydro derivatives	(4)dihydro derivatives
Stretch: 1.2812 Bend: 20.5725 Stretch-Bend: -0.8364 Torsion: 7.6783 Non-1,4 VDW: -1.4347 1,4 VDW: 4.2473 Dipole/Dipole: 0.3778 Total Energy: 31.8859 kcal/mol	Stretch: 1.2442 Bend: 20.8474 Stretch-Bend: -0.8355 Torsion: 9.5152 Non-1,4 VDW: -1.5540 1,4 VDW: 4.3354 Dipole/Dipole: 0.4491 Total Energy: 34.0018 kcal/mol	Stretch: 1.2836 Bend: 19.7407 Stretch-Bend: -0.8322 Torsion: 10.9390 Non-1,4 VDW: -1.2310 1,4 VDW: 5.6317 Dipole/Dipole: 0.1621 Total Energy: 35.6939 kcal/mol	Stretch: 1.0973 Bend: 14.5063 Stretch-Bend: -0.5494 Torsion: 12.4976 Non-1,4 VDW: -1.0512 1,4 VDW: 4.5127 Dipole/Dipole: 0.1407 Total Energy: 31.1539 kcal/mol

Discussion

Diels Alder Products (1&2)

Comparing the endo and exo Diels Alder product the higher energy conformer (kinetic product) is endo product. This product features higher torsion strain making it higher in energy. This can be seen from the adjacent atoms where there is a greater interaction as there are more carbons.

Although exo Diels Alder is the thermodynamically more favourable product in reality the endo Diels alder is favored due to interactions which stabilize the transition state. Even so endo Diels alder products can (as in this case) be higher in energy, this is an example of the Curtin-Hammet principle.

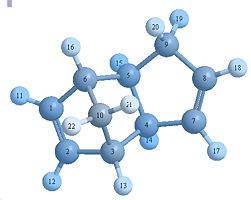
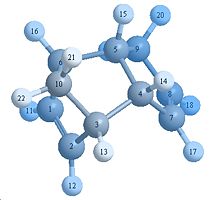
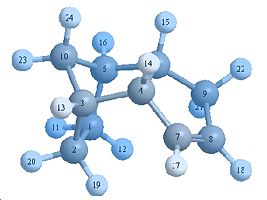
Dihydro Derivatives

3 has a higher in energy due to bending and an increase in 1,4 van der waals forces. From the molecule itself this strain arises due to close van der waals surface proximity

Space Filling Models of 3&4

(3)dihydro derivatives	(4)dihydro derivatives

Looking at the space filling orbital it can be seen that molecule 4 has the bottom 3 hydrogen’s more spread out with lesser interactions while in molecule 3 has more predominant 1,4 interactions. This shows that product 4 is the more thermodynamically stable isomer.

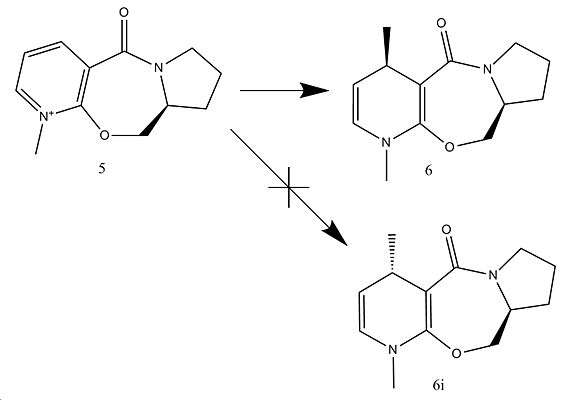
Stereochemistry of Nucleophilic additions to pyridinium rings

In this section selectivity of nucleophilic addition can be seen in the reaction below.

From looking at a 2 dimentional perspective it is not quite so obvious why the reaction gives the predominant major product 6 but by using Chembio 3D relative structures can be analysed and sterics can be taken into account with relative accuracy.

(5)Optically active derivative of prolinol	(6)Product from reaction of 5 with MgMeI	(6i)Isomer of 6
Stretch: 1.1674 Bend: 11.5000 Stretch-Bend: 0.0533 Torsion: 4.9593 Non-1,4 VDW: -1.9380 1,4 VDW: 11.9299 Charge/Dipole: 2.6622 Dipole/Dipole: -3.9769 Total Energy: 26.3571 kcal/mol	Stretch: 1.4724 Bend: 14.6292 Stretch-Bend: 0.1468 Torsion: 5.4157 Non-1,4 VDW: -1.9563 1,4 VDW: 13.3655 Dipole/Dipole: -4.1172 Total Energy: 28.9561 kcal/mol	Stretch: 1.4263 Bend: 14.4801 Stretch-Bend: 0.1459 Torsion: 5.2972 Non-1,4 VDW: -2.3221 1,4 VDW: 13.2876 Dipole/Dipole: -4.0355 Total Energy: 28.2795 kcal/mol

From analysis of the relative energies of 5,6 and 6i it can be seen that there is very little energy difference. Hence product 6 is not due to a thermodynamic result but more so a kinetic one. Having a closer look into the structure and reaction mechanism gives a more detailed indication of this phenomenon.

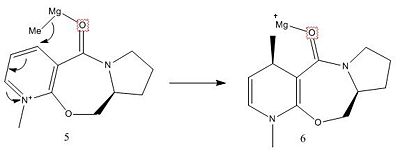
(6 planar view-red = oxygen, to the right of oxygen is the planar pyridine ring, to the left is the rest of the molecule)

In this reaction the Metal Magnesium coordinates to the carbonyl oxygen, since this oxygen, when in the lowest conformer, is slightly out of line with the pyridine ring, because of this, the metal and nucleophile (Me+) are more accessible and possible for attack on one face more than the other. Since both isomers are comparably relatively equal in energies the outcome means there is no preference for any actual isomer but the underlying sterics decide the conformer.

Mechanism

As stated above, the metal first coordinates to the oxygen and attacks in a concerted fashion.

Chirally Masked Amides

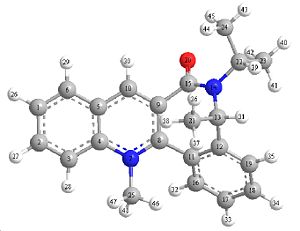
Being quite similar to the previous experiment the molecule 7 also comes out with high selectivity for one isomer.

Stretch: 1.5074 Bend: 6.2769 Stretch-Bend: 0.3191 Torsion: -5.4185 Non-1,4 VDW: -2.3313 1,4 VDW: 17.5823 Charge/Dipole: 2.4094 Dipole/Dipole: -4.7901 Total Energy: 15.5552 kcal/mol	Stretch: 1.6440 Bend: 12.7566 Stretch-Bend: 0.5256 Torsion: -8.7915 Non-1,4 VDW: -5.8065 1,4 VDW: 20.1786 Dipole/Dipole: -6.7937 Total Energy: 13.7129 kcal/mol	Planar view of 7 (shows the side which the Oxygen(20) resides)

The stereo selectivity in this case is a lot more obvious when a 3 dimensional representation of the molecule is analysed. The oxygen on the CO bond again is bound to one side, for this molecule is it a much more obvious (larger angle) steric hindrance on behalf of the oxygen atom. Another reason for attack at once face can be seen in the stability of the final product, In the literature the product 8 shows good interactions between the nitrogen of the nucleophile and the methyl (carbon number 32).

General Notes

On producing molecular representations of 8 afew difficulties were encountered. benzene rings are known to be very rigid and planor molecules. but as can be seen from the screen shot below this is not always the case.

(hydrogens on carbons 1,2,3,4,5 and 6 are not planor)

This shows there is not a high enough force constant for benzene rings. A limitation from using chembio 3D is that it does not take into account the strength or regidty of the benzene rings. such observations must be clearly seen to gain good estimates or data from molecules when using Chembio3D.

The mechanism proceeds via a similar procedure to that of molecule 5 to 6.

References

1. A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016
2. Leleu, Stephane; Papamicael, Cyril; Marsais, Francis; Dupas, Georges; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI:10.1016/j.tetasy.2004.11.004

Bridgehead Alkene Reactivity

Here the use of energy is just to provide a guideline to the lowest possible energy conformer. But as will be seen below these values is less important and other values such as relative angles will help a lot more in assessing real phenomena.

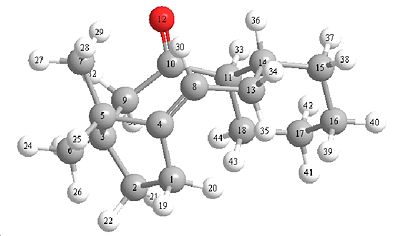
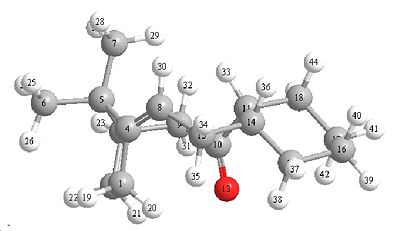
(10)carbonyl pointing up with the bridge	(11)carbonyl pointing down against the bridge
Stretch: 2.6751 Bend: 15.8061 Stretch-Bend: 0.3933 Torsion: 18.2388 Non-1,4 VDW: -1.0294 1,4 VDW: 12.6617 Dipole/Dipole: 0.1511 Total Energy: 48.8969 kcal/mol	Stretch: 2.5771 Bend: 10.8517 Stretch-Bend: 0.3274 Torsion: 19.6523 Non-1,4 VDW: -1.4769 1,4 VDW: 12.5381 Dipole/Dipole: -0.1805 Total Energy: 44.2892 kcal/mol

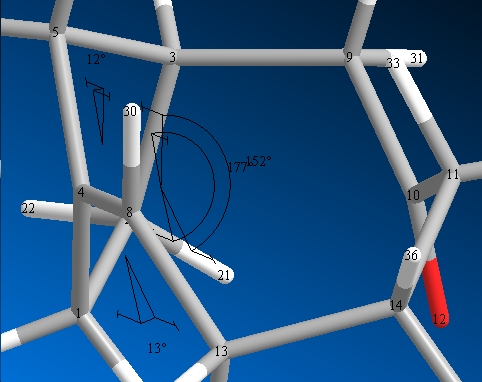
The Molecules above show a specail type of isomerism caused by steric boundaries called atropisomerism. Alkenes become more reactive when the dihedral angle from twisting is increased. This twisting about an alkene bond makes the alkene more reactive due to a lowering of the energy gap from homo to lomo.

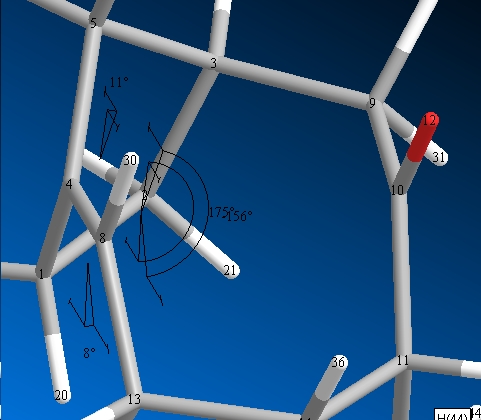
Hyper stable alkenes are alkenes which form at the bridgehead of a molecule not only this but the alkene has to also be more stable than it would be normaly (hence hyper stable), an example of an non hyperstable alkene but still an alkene at a bridge head but (using molecule 10) if carbon number 8 was directly bonded to 9, this would increase the strain around the alkene so much to make it very unstable. These are generally very unreactive due to less strain. From looking at the dihedral angles it can be seen that isomer 11 has larger dihedral angle strain and thus this isomer is more reactive.

Dihedral Angles

(10)	(11)

This shows that isomer 11 has an overall larger strain, and hence a lowering of the homo lumo splitting and hence more reactive as its easier for the external processes to promote electron transferre from the homo to the lumo.

References

1. J. G. Vinter and H. M. R. Hoffman, J. Am. Chem. Soc., 1974, 96, 5466 DOI:10.1021/ja00824a025
2. Wilhelm F. Maier, Paul Von Rague Schleyer,J. Am. Chem. Soc., 1981, 103 (8), pp 1891–1900 DOI:10.1021/ja00398a003

Hydrolysis of a Peptides

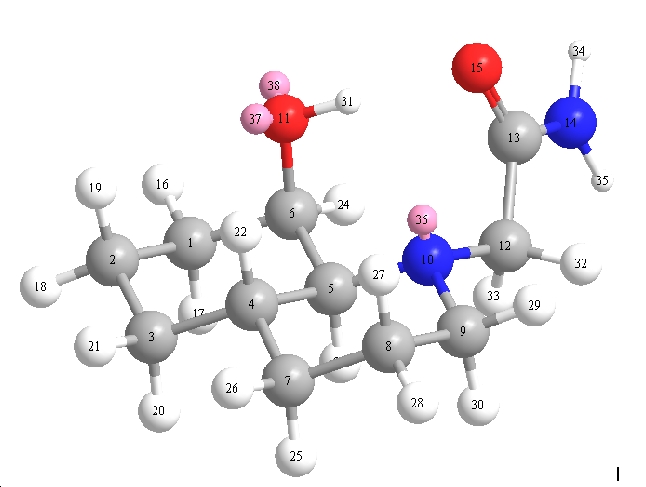
Rates of reactions in hydrolysis are dominated by specific features present on the substrate. In this experiment molecules 13 and 14 (trans and cis isomers) will be examined.

(13)Equitorial	(13)Axial	(14)Equitorial	(14)Axial
Stretch: 1.6923 Bend: 5.1628 Stretch-Bend: 0.5278 Torsion: 9.4255 Non-1,4 VDW: -7.4139 1,4 VDW: 10.0459 Dipole/Dipole: -6.3325 Total Energy: 13.1078 kcal/mol	Stretch: 1.6273 Bend: 8.2302 Stretch-Bend: 0.6453 Torsion: 12.0642 Non-1,4 VDW: -8.0861 1,4 VDW: 10.2034 Dipole/Dipole: -4.8635 Total Energy: 19.8208 kcal/mol	Stretch: 1.5408 Bend: 3.2424 Stretch-Bend: 0.4872 Torsion: 7.2415 Non-1,4 VDW: -8.1421 1,4 VDW: 9.7535 Dipole/Dipole: -5.0818 Total Energy: 9.0415 kcal/mol	Stretch: 1.5460 Bend: 5.1207 Stretch-Bend: 0.5527 Torsion: 8.6952 Non-1,4 VDW: -7.0491 1,4 VDW: 9.5922 Dipole/Dipole: -6.4661 Total Energy: 11.9917 kcal/mol

From just looking at the energies of the isomers in 13 and 14, the difference in the energies shows that 13 has a larger energy gap then 14. this increased difference would increase the reactivity of the molecule and thus increase the rate of reaction.

Other factors which have to be taken into account, since this is a reaction of a nucleophile (R-OH) with a carbonyl group, the Burgi Dunitz angle has to be satisfied. So by observing the relative geometries of the structures it can be seen that one factor which holds back this reaction from taking place would be due to a type of conformational lock by hydrogen bonding. If hydrogen bonding with in the molecule is great (if the geometry is so that the R-OH and the O=C-R are close then the hydrogen bonding will start to dominate. in molecule 14 this is exactly what is seen for both axial and equatorial isomers, the hydrogen is bonded with the C=O carbonyl thus inducing a lock and the R-OH can no longer react in a 109 degree Burgi Dunitz angle. hydrogen bonding in molecule 13 is a lot less prominent and so the R-OH is is not free to attack as a nucleophile.

The hydrolysis in a uni-molcular system is much faster due to the constant closer proximity of the reacting molecules. In a bi-molecular system the 2 components have to find each other, then once they have found each other they both have to have enough energy to react. But since in a intramolecular/uni-molecular reactions the reacting parts are both on the same molecule, the effective concentration is thus a lot higher and meet a lot more often to react.

Regioselective Addition of Dichlorocarbene

In this section the use of molecular modelling and optimisations of energies can be very useful in predicting relative bond strengths, molecular orbital’s, thus orbital interactions and from these a relative IR can be produced to indicate these bond strengths of the starting product and the target product.

12	12a	12b

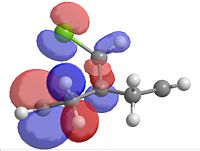
12 is the starting product and 12a and 12b are the monohydrogenated alkene products. From looking at the structure of the starting material and the possible products an indications to which the favoured product can be found by looking at the molecular orbital’s.

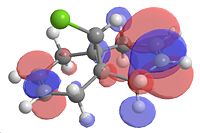
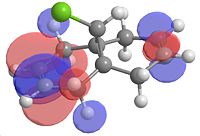
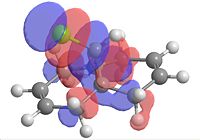
Homo-1	Homo	Lumo	Lumo+1	Lumo+2

Molecule	12	12a	12b
C-Cl	772.634, 25.2414	757.681, 27.4001	782.384, 22.2202
C-Cl	931.88, 7.6399	926.52, 9.4959	912.84, 7.0891
C=C exo	1740.76, 4.1444	1740.63, 3.1983	n/a
C=C endo	1760.91, 3.9037	n/a	1757.60, 5.0198

all IR stretches are quoted in cm^-1 (wave numbers) (first number = frequency and second number = relatvie intensity)

IR spectra

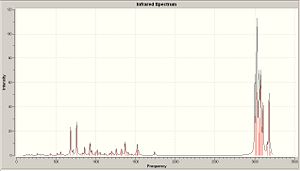
12	12a	12b

Conclusion

From looking at the Homo-1 the orbital is shown to be such that the overlap is antiperiplanor to that of the C-Cl σ* orbital. The largely diffuse π system of the exo C=C, due to the geometry of the molecule, can thus donate into this orbital, weakening the C=C exo bond (this can be seen in homo-1). This can be seen clearly on the IR vibrations modelled using the optimised geometry. The exo carbon double bond in 12 is clearly lower in energy than that of the endo (as explained earlier, due to the donation into the C-Cl σ* orbital. In this case of the C-Cl stretches, the effect of the mono hydrogenated product can also be seen with the weakening and strengthening effects due to this orbital interaction. For product 12a, the homo now is the orbital which is interacting with the C-Cl σ* orbital and this makes the C-Cl stretch weaker, which is what is observed.

References

1. 12 IR: DOI:10042/to-1684
2. 12a IR: DOI:10042/to-1679
3. 12b IR: DOI:10042/to-1691

Mini Project

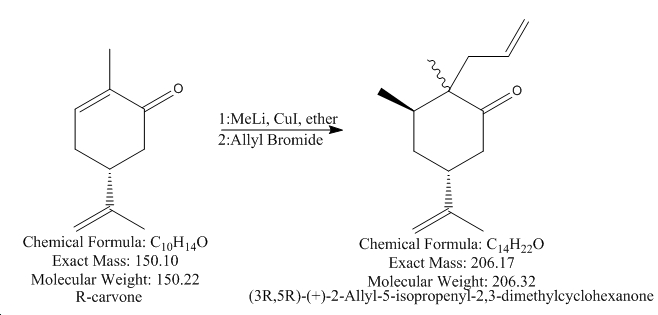
The mini project of choice was found in a reaction involving a presonal favourite chemical Carvone. Reaction scheme:

This reaction is a Nucleophilic Addition using an organo lithum reagent. From first glance MeLi would give a hard base/nucleophile which would ideally attack at the carbonyl carbon into the C-O pi* orbital but this does not occour to due to a simple transmetallation with the CuI

The new softer Methyl now not only doesnt act as a base (removing hydrogens) but also attacks at the softer electrophile at the C=C double bond.

Mechanism

This mechanism shows the first attack of the methyl at the C=C double bond, initially looking at the 2D representation it is not so clear to why there isn't an isomer produced. using Chembio 3D relative energies and geometries can be easily calculated

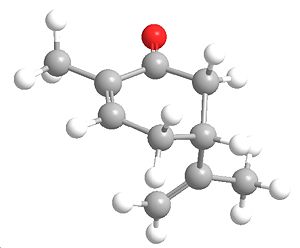
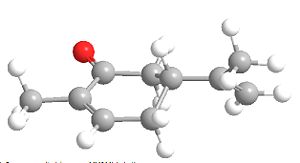
R-Carvone Axial	R-Carvone Equitorial
Stretch: 0.5918 Bend: 1.7438 Stretch-Bend: 0.1178 Torsion: -0.6410 Non-1,4 VDW: -0.8546 1,4 VDW: 5.7873 Dipole/Dipole: -0.6696 Total Energy: 6.0755 kcal/mol	Stretch: 0.5053 Bend: 1.4168 Stretch-Bend: 0.0932 Torsion: -2.1092 Non-1,4 VDW: -1.1541 1,4 VDW: 5.8595 Dipole/Dipole: -0.6220 Total Energy: 3.9895 kcal/mol

From looking at the energies the obvious more stable isomer will be the equitorial, but this molecule isnt quite a chair shaped structure due to the double bond and hence the energy of the inversion barrier is this low, this explains why only one product is obtained from the first step.

Looking at the second step of the reaction it can be seen that the electrons from the intermediate can then attack from either side of the ring system and thus give 2 isomers.

Products

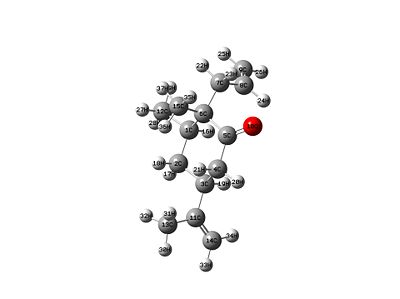
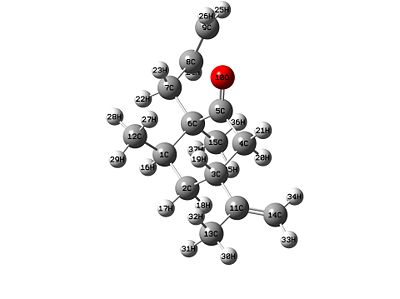
Product/isomer X	Product/isomer Y
Stretch: 1.5408 Bend: 2.6070 Stretch-Bend: 0.3626 Torsion: 7.0838 Non-1,4 VDW: -2.5840 1,4 VDW: 9.6468 Dipole/Dipole: 0.4423 Total Energy: 19.0993 kcal/mol	Stretch: 1.5966 Bend: 2.5168 Stretch-Bend: 0.3717 Torsion: 8.8817 Non-1,4 VDW: -2.1383 1,4 VDW: 9.5661 Dipole/Dipole: 0.4437 Total Energy: 21.2382 kcal/mol

Having a look at the energies it can be seen which one is more thermodynamically stable. This means that the lower energy product is isomer X.

Infrared

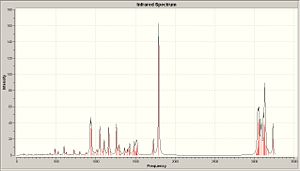
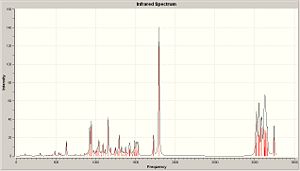
Computated IR of X	Computated IR of Y

key: (frequency, intensity) all frequencies are quoted in cm^-1

stretch	Product X	Product Y
C=O	1792.47, 163.583	1797.16,140.643
C=C	1723.15, 6.5747	1727.18, 74444

Lit:IR (neat): 1705 (C=O), 1640 (C=C). These values are not so close to literature values. computational IR seems to be only able to give predictions of certain stretchs if there is a direct molecule for which it can be compared. e.g. Isomers X and Y, the C=O stretch for both are different this is because in X the C=O donates into the π* antibonding orbital of the C=C, this donation could be seen as a favourable stablising energy and thus showing a more thermodynamically stable product X. This donation would weaken the C=O bond and weaken the C=C bond but intramolecular interactions which orginally wouldnt be seen are shown to be stalising, a type of anomeric effect. (non-bonding electrons on the oxygen donating into π* C=C causing a stablising effect).

By doing an IR computationally, thermal energy can be very roughly calculated.

Product X: Sum of electronic and thermal Free Energies= -621.673543au = -390100.1482kcal/mol Product Y: Sum of electronic and thermal Free Energies= -621.633648au = -390075.1141kcal/mol

(1 Hartree = 627.5 kcal/mol)

From looking at the difference in energies calculated from the IR scan, the energy gap shown is significantly big and shows that the lower energy product, the more thermodynamically stable product is product X by 25.03kcal/mol.

This energy difference further backs up the point that the geometry of X causes a stablising effect by donation into π* orbitals on the C=C.

To further back up the point of this stablisation effect, the molecular orbitals for both of these molecules were calculated.

X-homo	Y-homo

In isomer X the oxygen can clearly donate into the π* antibonding orbital of the C=C but in Y the oxygen is not directly above the C=C bond and thus cannot.

Steric factors

Intermediate

		Pentahelicene
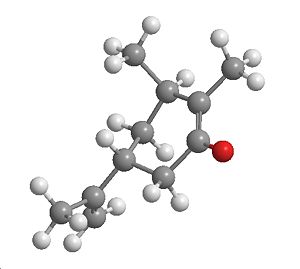
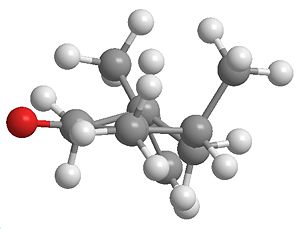
Intermediate	Side on view (use this when referring to top and bottom)	jmol

Sterics are a common factor in deciding the outcome of a reaction (as in the first part to this reaction). By looking at the intermediate, since this molecule will be present before reacting to give the product, it can be clearly seen if there is a specific preference to one isomer over the other, a jmol was inserted to make it more easily visable.

The intermediate does appear to have steric interactions when attacking the top side but the bottom shows alot less crowdedness, which intern could result in preferential attack on the bottom face.

The molecular orbitals of molecules can also help in deciding whether or not a molecule will react at a certain atom on a molecule.

MO of the homo also gives an idea to the electron density to which the electrons reside on the molecule, in this case the electrons are even in distribution, thus doesnt show much in the case of selectivity.

Products

Pentahelicene	Pentahelicene
X	Y

The product doesnt show much steric hinderence in either case, but as show before, in the transition state when attacking the allylbromide there will be a sterically more favourable route and this route is the one with attack to give product X.

Calculated NMR

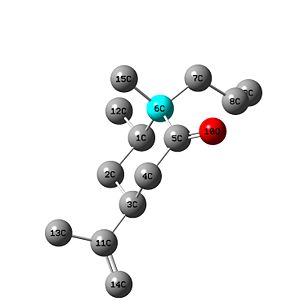
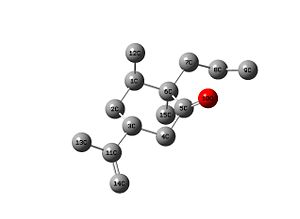
Product X	Product Y
5, 212.05 11, 145.12 8, 133.61 9, 114.47 14, 111.16 6, 52.66 3, 47.20 4, 43.59 7, 41.46 1, 37.24 2, 34.38 15, 20.90 13, 18.24 12, 16.38	5, 212.64 11, 146.20 8, 132.74 9, 118.21 14, 108.38 6, 54.04 1, 44.62 3, 43.42 4, 42.55 7, 38.926 2, 35.28 13, 24.01 15, 22.25 12, 16.61

When refering to the chemical shifts please use the pictures at the top of the table. (the first number is related to the atom and the second number is the chemical shift in ppm, this is a Carbon 13 nmr using "TMS mPW1PW91/6-31G(d,p) CDCl3 GIAO" as the reference, all hydrogen's are emitted to improve clarity.)

X	Y	lit
5, 212.05 11, 145.12 8, 133.61 9, 114.47 14, 111.16 6, 52.66 3, 47.20 4, 43.59 7, 41.46 1, 37.24 2, 34.38 15, 20.90 13, 18.24 12, 16.38	5, 212.64 11, 146.20 8, 132.74 9, 118.21 14, 108.38 6, 54.04 1, 44.62 3, 43.42 4, 42.55 7, 38.926 2, 35.28 13, 24.01 15, 22.25 12, 16.61	213.4 (s, C=O), 146.8 (s, ~H2), 133.2 (d, CH=CH2), 117.0 (t,CH--CH2), 109.7 (t, C=CH2), 51.1 (s, C-2), 42.2, 41.3, 39.9, 36.0 (d), 32.2 (t), 20.4 (q), 18.3 (q) 15.23 (q) [3 x CH3]

From comparing the computer values with the literature, at first both look very similar. But as the molecule stands the geometry might not be quite correct to real values. The value which should be different in both cases is carbon number 6, this is because this is the chiral center. This center in the molecule would show a difference in both isomers, as it is no longer in the same electronic environment. Having a look at the values isomer x has the closest value to that of the literature for carbon 6 (the chiral center). This shows that the isomer formed is isomer X.

Optical rotation

Product X = [Alpha]D = +67.82 deg

Product Y = [Alpha]D = -193.52 deg

literature for Product X = [Alpha]D = +37.0 deg (C 1.2, CHCI3)

From doing an optical rotation, computational calculations were able to predict the correct sign of the rotation but the amount at which was rotated is less accurate.

Conclusion

From using computational methods a relatively accurate representation of the geometry, molecular orbitals and NMR can be found. Using these main factors, the outcome of the reaction was able, in terms of which isomer would be produced, could be recognized with confidence. By using literature results, the resulting C13 NMR and isomer ratios can be checked against the computed method and the isomer of choice. In this case the reaction proceeds to give 9:1 of X:Y respectively. This shows that it is possible to predict the outcome by using computational methods. Computational methods can also be used in predicting optical rotations even though quantitatively not accurate, it correctly predicted the sign. If time premitted, more accurate calculations could have been run with higher basis sets to give more accurate data and better approximations. Despite this the spectral and physical data recieved was quite close to that of the literature and accurate predictions were able to be made with out even doing the reactions.

References

1. NMR prod 1:DOI:10042/to-1689
2. NMR prod 2:DOI:10042/to-1690
3. IR & Thermal free energies product 1 DOI:10042/to-1721
4. IR & Thermal free energies product 2 DOI:10042/to-1722
5. Optical rotation product 1 DOI:10042/to-1725
6. Optical rotation product 2 DOI:10042/to-1726
7. Chiral synthons from carvone, Part 34. For part 33, see: Srikrishna, A.; Santosh J. G. Chem. Commun., 1998, 0000. For part 32, see: Srikrishna, A.; Vijaykumar, D. Tetrahedron Lett., 1998, 39, 5833. :DOI:10.1016/S0040-4020(98)00672-3

Notes

Full energies have been left as is and not cut out for reference and my not be used in any explanation. All energies unless stated are in units of au, IR frequencies will be quoted in cm^-1 and all chemical shifts in C13 NMR are quoted in ppm. All jmols were added to help understand the stereochemisty of a molecule and see possible areas preferential attack due to sterics.