Rep:Mod:gkuytuyg
Introduction
When Gaussian calculates a minimum, it varies each nuclear position as a function of the total energy of the molecule and finds the geometry such that the energy is lowest. The transition state is the maximum energy geometry on the reaction pathway between the reactants and products.
At a minimum the gradient is zero since it is a stationary point and consequently the curvature is upwards on either side. The first derivative of the energy with respect to each nuclear coordinate is equal to zero at a minimum and second derivative is positive.
Frequency calculations are useful since at a minimum there will be no imaginary frequencies. This is because the frequencies are calculated using a harmonic oscillator model where the force constant is equal to the second derivative of the energy with respect to nuclear positions and the frequency is proportional to the square root of the force constant. If it is a minimum the second derivative will be positive giving all positive frequencies. However for a transition state there will be an imaginary frequency since the curvature is downwards so the second derivative will be negative, hence giving an imaginary frequency.
Nf710 (talk) 16:13, 4 November 2016 (UTC) Good understanding, of the 1 d harmonic oscillator
Exercise 1
Nf710 (talk) 16:18, 4 November 2016 (UTC) YOu could have shown the ordering of the MOs of the products too as well as the interactions
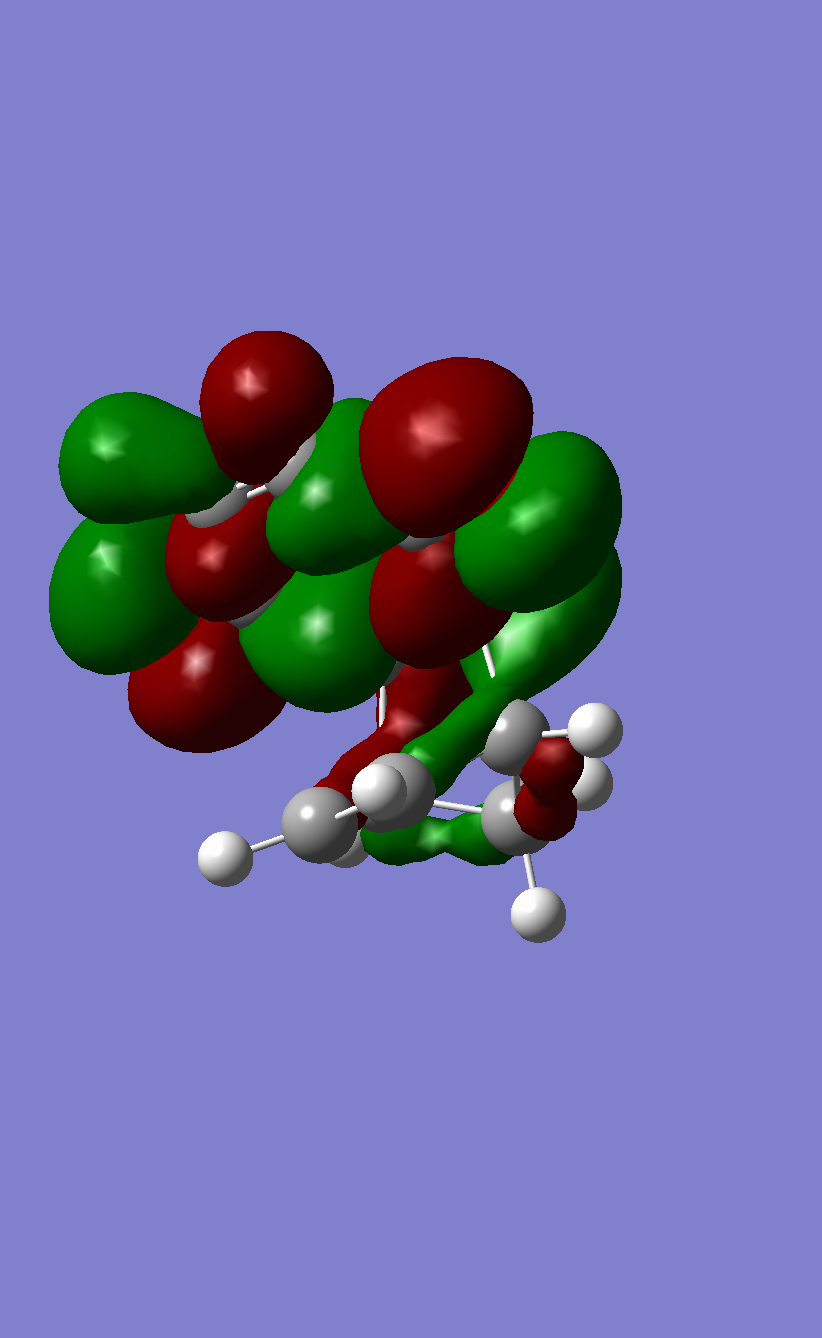
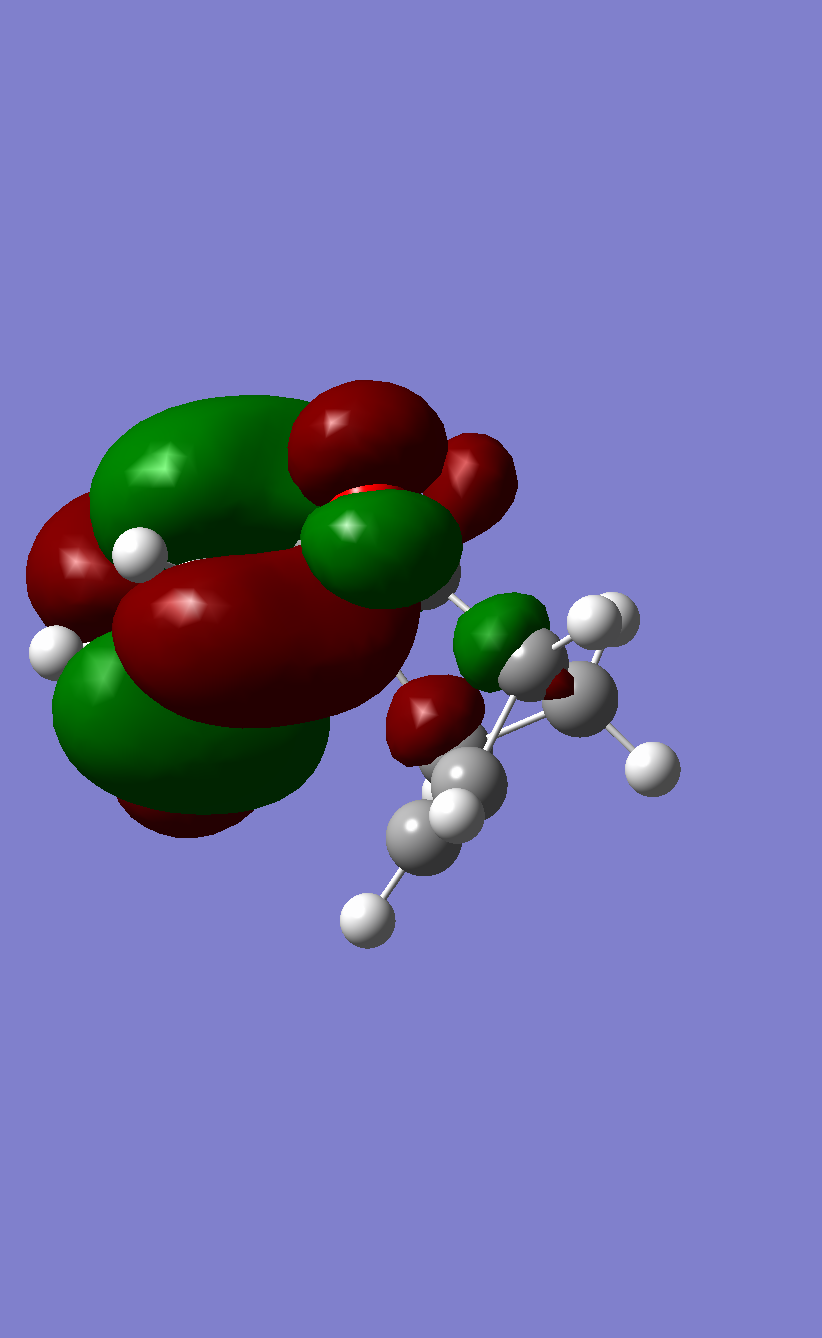
The HOMO of Butadiene calculated with B3LYP |
The LUMO of Butadiene calculated with B3LYP |
The HOMO of Ethene calculated with B3LYP |
The LUMO of Ethene calculated with B3LYP |
The HOMO of the transition state calculated with PM6 |
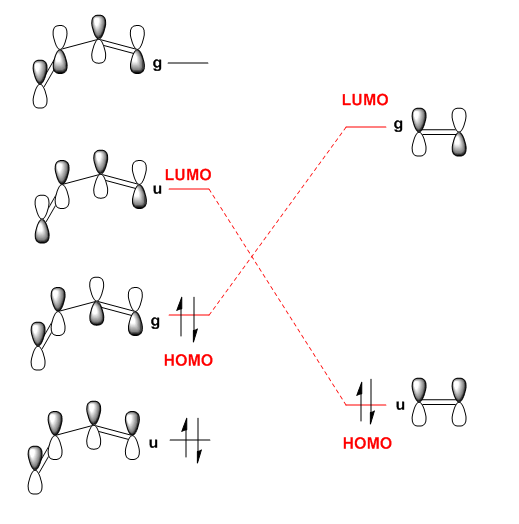
It can be seen that the drawn MO diagram HOMOs and LUMOs correspond roughly to those that Gaussian produced. The dotted red lines show the possible MO interactions in the Diels Alder reaction. For any reaction only MOs of the same symmetry may overlap. This is shown by the parity labels g and u, otherwise the orbitals interfere destructively and become antibonding making new bond formation impossible and forbidden. When the symmetry is the same these reactions are allowed. Woodward-Hoffman rules are a way of working out whether a reaction is thermally allowed or not based on this principle. for u-u and g-g interactions the overlap integral will be non-zero. For u-g interactions it will be zero.
| Bonds in Reactants /Å | Bonds in Transition State /Å | Bonds in Product /Å |
|---|---|---|
| Diene C=C 1.33918 | Diene C~C 1.37978 | Diene C-C 1.50085 |
| Diene C=C 1.33918 | Diene C~C 1.37975 | Diene C-C 1.50083 |
| Diene C-C 1.47013 | Diene C~C 1.41111 | Diene C=C 1.33700 |
| Ethene C=C 1.33087 | Ethene C~C 1.38176 | Ethene C-C 1.53464 |
| - | - | New C-C 1.53700 |
| - | - | New C-C 1.53722 |
The average C-C sp3 bond is 1.54Å and for C=C sp2 it is 1.47Å. For the diene the single bond is shorted than in a normal single C-C bond due to the conjugation of the double bond, and the carbons involved being sp2 so the hybrid orbital forming the single bond has more s character than would a regular sp3 C-C bond. These bond length calculations demonstrate the breaking and making of bonds over the course of the reaction through bond lengthening going from a double to single bond and bond contraction with going from a single to a double bond.
The Van der Waals radius of carbon is is 1.70Å. In the transition state the distance between the centres of the carbon atoms which form bonds is 2.11435Å. Given the radius of carbon atoms, at this distance apart their radii would overlap by 0.64Å on each
the animation of the vibration corresponding to the reaction path at the transition state shows the bond formation as being synchranous, as is expected of a pericyclic reaction:
The LUMO of the transition state calculated with PM6 |
The lowest possible frequency is an asymmetric stretch which is asynchronous
Nf710 (talk) 16:32, 4 November 2016 (UTC) Would have been good to include the animation, but this section was generally well done.
Exercise 2
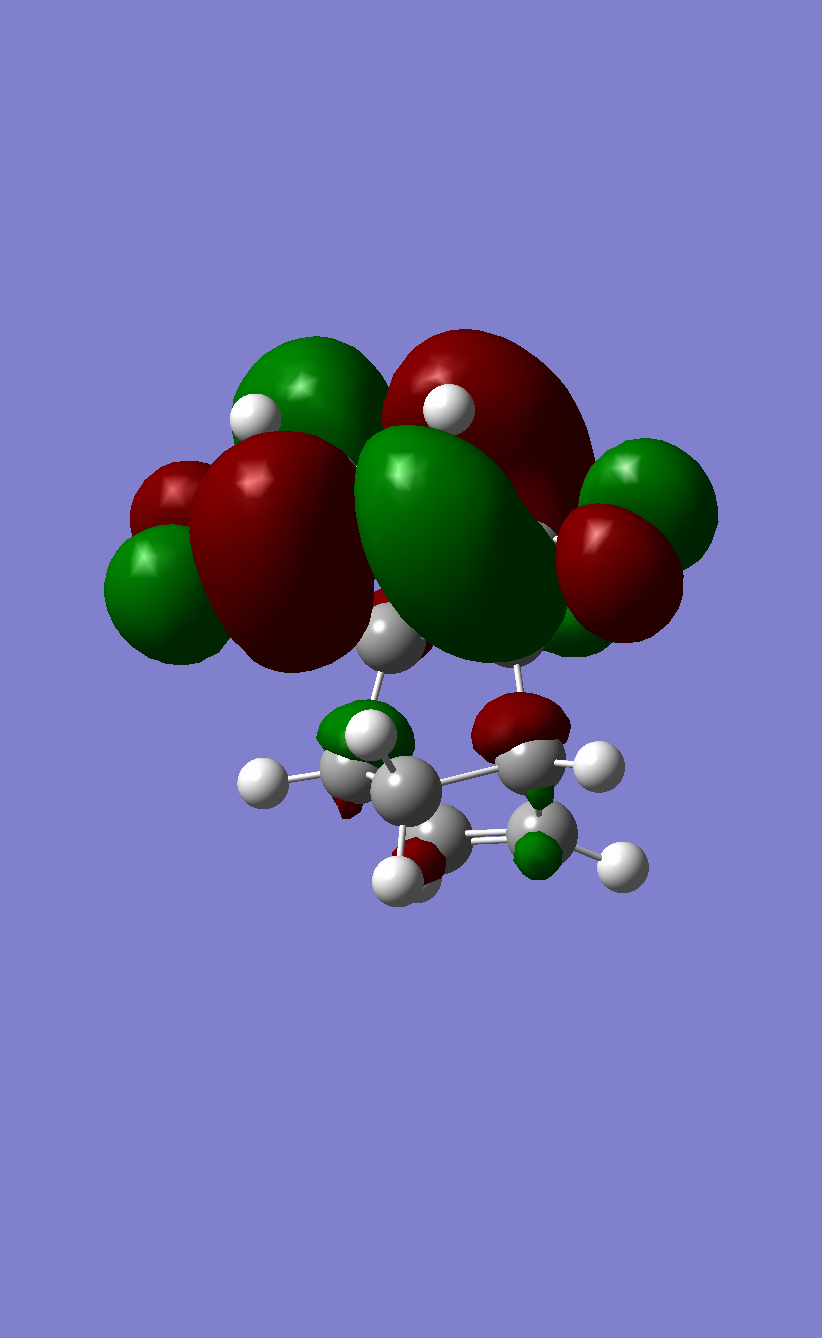
(These are the MOs of the products. They are also huge images making it difficult to compare them Tam10 (talk) 12:26, 31 October 2016 (UTC))
A normal demand Diels-Alder reaction involves the diene acting as the nucleophile since its HOMO is closer to the LUMO of the dieneophile. This is facilitated by electron withdrawing groups on the dieneophile which the lower the MO energies. In inverse demand Diels-Alder reactions the dieneophile acts as the nucleophile, since its HOMO has a better overlap with the LUMO of the diene.
In this reaction of of benzoquinone with cyclopentadiene it is normal demand since the HOMO of the diene is -0.21154, which is higher in energy than the HOMO of the dieneophile which is -0.27061. The energy gap between the HOMO of the diene and the LUMO of the dieneophile is 0.0815 which is smaller than the gap between the HOMO of the dieneophile and the LUMO of the diene, hence it is a normal demand Diels-Alder.
The sum of electronic and thermal free energies are as follows for the endo and exo reactants, products and transition states. From which the reaction barrier (TS-reactants) and reaction energy (products-reactants) were calculated:
| Endo | Exo | |
|---|---|---|
| Reactants Energy /Ha | -575.418836 | -575.418836 |
| Transition State Energy /Ha | -575.383855 | -575.381305 |
| Product Energy /Ha | -575.427051 | -575.428695 |
| Reaction Barrier /Ha | 0.034981 | 0.037531 |
| Reaction Energy /Ha | -0.00821499999 | -0.00985899999 |
(The exo product energy is lower than expected. Are you sure the basis set was the same? Tam10 (talk) 12:26, 31 October 2016 (UTC))
From this data it is clear that the endo reaction is kinetically favourable since the transition state is lower in energy and the reaction barrier is smaller. However the energy of the exo product is the lowest in energy and the overall reaction is shown to be more exothermic for the exo product. This shows that it is the thermodynamic product due to that product having less steric clash.
In the endo transition state secondary orbital interactions can be seen. These have the effect of stabilising the endo transition state lowering the activation energy. This compensates for the higher steric clash in the endo transition state.
Nf710 (talk) 16:42, 4 November 2016 (UTC) Your TS energies are correct and you used the correct energy of the reactants from the IRC and not at infinite seperation. I don't know what happened to your exo products because then energy is wrong, I dont have your log file to check why. Also label your figures more clearly
Exercise 3
For the cheletropic reaction the the product was used as a starting point then the reactants derived through finding the transition state and running an IRC backwards to get the reactants. The images below show the procucts, transition state and reactants respectively:
As it goes from reactants to the transition state the terminal C=C bonds lengthen and the ones in side the ring increase in double bond character. This can be seen in Gaussian by one of the double bonds changing to a dotted bond in the transition state, indication the bonding character is somewhere between a single and double bond.
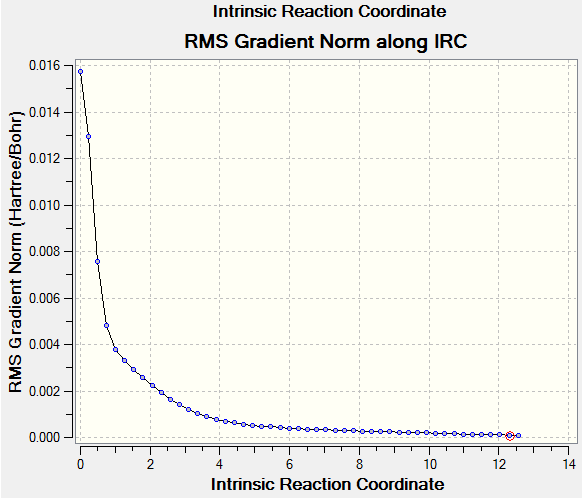
The reaction path of the IRC going from transition state to reactants is below:
The Diels-Alder reaction kept failing to properly optimise when tried from the products or reactants as the starting point and I ran out of time, so no comparison was possible.
(The gradient at IRC=0 should always be 0. This indicates you weren't starting at the TS Tam10 (talk) 12:26, 31 October 2016 (UTC))