Rep:Mod:gjsmodule3 jackanackanory

Module 3 Jackanackanory!

The Cope Rearrangement Tutorial

Optimising the Reactants and Products

Introduction

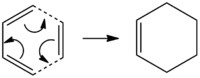
The Cope Rearrangement reaction is a pericyclic reaction, i.e. a concerted rearrangement of bonds proceeding via a fully conjugated cyclic transition state, and it is this rearrangement reaction which will be studied in this section.

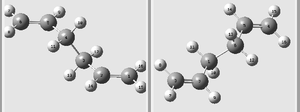
The aim of the following calculations is to find the most stable reactant/product conformer, and the lowest energy transition state in order to find the preferred reaction mechanism. Below is a table representing the energies of the different conformers of 1,5-hexadiene.

Figure 1: Table reporting the relative energies of different conformers of 1,5-hexadiene

Description of conformer	Jmol	Picture of conformer	Point Group	Energy/Hartrees HF/3-21G	Relative energy / kcal/mol	Link to summary of HF/32-1G optimisation calculation
Anti 1			C2	-231.69260	+0.04	Link
Anti 2			Ci	-231.69254	+0.08	Link
Anti 3			C2h	-231.68907	+2.25	Link
Anti 4			C1	-231.68907	+1.06	Link
Anti 5			C2h	-231.68540	+4.56	Link
Gauche 1			C2	-231.68772	+3.10	Link
Gauche 2			C2	-231.69167	+0.62	Link
Gauche 3			C1	-231.69266	0.00	Link
Gauche 4			C2	-231.69153	+0.71	Link
Gauche 5			C1	-231.68962	+1.91	Link
Gauche 6			C1	-231.68916	+2.20	Link

In order to obtain the "Anti 5" conformer, no "cleaning" was conducted before doing the HF/3-21G optimisation.

DFT B3LYP/6-31G (d) Optimisations of the Anti 1, Anti 2 and Gauche 3 Conformers

Figure 2: The Cope Rearrangement

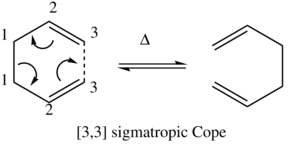
As it can be seen from figure 1, the lowest energy conformer calculated using the HF/3-21G method was the Gauche 3 conformer, with the Anti 1 and Anti 2 conformers also having similarly low energies. As the objective in this section is to locate the low-energy minima and transition structures on the C₆H₁₀ potential energy surface in order to determine the preferred reaction mechanism of the Cope rearrangement (figure 2, right), only the conformers with the lowest potential energy were selected for further optimsiation and analysis. The results from the DFT B3LYP/6-31G (d) optimisations of the lowest energy conformers can be seen in figure 3 below.

Figure 3: Table showing the relative energies of three chosen conformers after DFT B3LYP/6-31G (d) Optimisation

Confromer	Jmol	Energy/Hartrees	Relative Energy / kcal/mol	Link to Summary	Link to D-Space
Anti 1		-234.61179	0.00	Link to summary	Link to D-space
Anti 2		-234.61170	+0.06	Link to summary	Link to D-space
Gauche 3		-234.61133	+0.29	Link to summary	Link to D-space

After conducing the DFT B3LYP/6-31G (d) optimisations on Anti 1, Anti 2 and Gauche 3, interestingly it can be seen that it is the Anti 1 conformer which is the most stable, and not Gauche 3. The point groups of each conformer are unchanged from the initial optimisations, suggesting that the geometries are unchanged (this can be seen visually by comparing the Jmols in figures 1 and 2). The geometries are unchanged and yet the order of stabilities have changed due to the increased accuracy of the optimisations, mostly tweaking the electronic structures of the conformers.

Upon further analysis of the two optimised structures of the anti 2 conformer, it was discovered that all the anti-periplanar dihedral angles were exactly 180^o for both of the optimised structures. However, when looking at the dihedral angle of the 4 carbon atoms at the end of the chains, the HF/3-21G optimised structure yielded a dihedral angle of 114.7^o where as the DFT B3LYP/6-31G* optimised structure gave a dihedral angle of 118.5^o. Therefore, the two different calculations produced conformers with very similar geometries. The HF/3-21G method somewhat neglects the electron correlation, certainly more so than the DFT B3LYP/6-31G* method and basis set, explaining the small difference in geometries.

However, these energies calculated thus far represent the bare potential energy surface and in order to compare them with experimentally determined values, some additional terms are required. Therefore, some frequency calculations were carried out using the same method and basis set on the three conformers.

DFT B3LYP/6-31G (d) Frequency Calculations

Figure 3: Table showing the relative energies of three chosen conformers after DFT B3LYP/6-31G (d) Frequency calculations at both room temperature and absolute zero

	298.15 K & 1.0 Atm.						0 K & 1.0 Atm.
Conformer	Link to D-space	Sum of electronic & zero-point energy/ Hartrees	Sum of electronic & thermal energies/ Hartrees	Sum of electronic & thermal enthalpies/ Harteres	Sum of electronic & thermal free energies/ Hartrees	Link to IR Spectrum	Link to D-space	Sum of electronic & zero-point energy/ Hartrees	Sum of electronic & thermal energies/ Hartrees	Sum of electronic & thermal enthalpies/ Harteres	Sum of electronic & thermal free energies/ Hartrees
Anti 1	Link to D-space	-234.46930	-234.46197	-234.46102	-234.50086	Link to IR Spectrum	Link to D-space	-234.46930	-234.46930	-234.46930	-234.46930
Anti 2	Link to D-space	-234.46921	-234.46187	-234.46091	-234.50082	Link to IR Spectrum	Link to D-space	-234.46921	-234.46921	-234.46921	-234.46921
Gauche 3	Link to D-space	-234.46869	-234.46146	-234.46052	-234.50011	Link to IR Spectrum	Link to D-space	-234.46869	-234.46869	-234.46869	-234.46869

From figure 3 above, it can be seen that at absolute zero there is no contribution from thermal energy, enthalpy or free energy and that therefore all these values are equal to the zero-point energy. This is indeed logical, as the classical definition of absolute zero is the point at which there is no thermal energy.

Figure 4: Showing the numbering of the atoms for two of the conformers

Anti 1	Gauche 3

Figure 5: σC-C/σ*C-C Orbital Interactions in the Anti 1 conformer

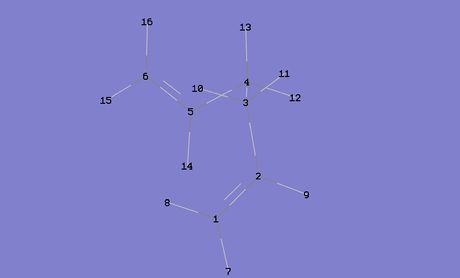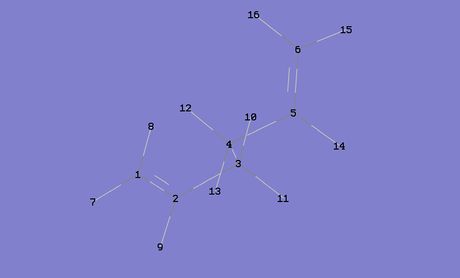
From the HF/3-21G optimisation calculations the Gauche 3 conformer was calculated to be the most stable conformer, but upon the more accurate and computationally demanding B3LYP/6/31G (d) optimisation calculations, it was realised that it was in fact the Anti 1 conformer that was the most stable. Therefore, some qualitative analysis was done on these two conformers in order to try and better understand the chemistry behind this. In figure 4 above, the atoms of the two conformers have been numbered; these are important reference points for the rest of this part of the discussion.

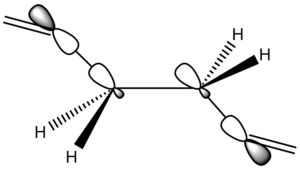
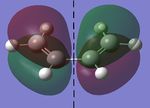
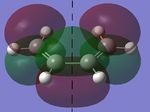
One potential reason for the Anti 1 conformer being more stable is more effective orbital overlap. The Anti 1 conformer should have two sets of σC-C/σ*C-C interacting orbitals and four sets of σC-H/σ*C-H interacting orbitals, where as the Gauche conformer should have two sets of σC-H/σ*C-H, two sets of σC-C/σ*C-H and two sets of σC-H/σ*C-C (a diagram depicting the σC-C/σ*C-C orbital interactions can be seen in figure 5 on the right). If the stabilising effects of these interactions were to be equated to butane, it would be the anti conformer that was stabilised the most It is also important to note that these interactions occur most strongly when the dihedral angle of the respective atoms is 180^o, but from looking at the dihedral angles of the atoms along the C(3)-C(4) bond in the two conformers, it can be seen that the bonds in the Anti 1 conformer are better aligned for orbital overlap (the dihedral angles of the two conformers can be seen in figure 6), the average dihedral angle along the C(3)-C(4) bond in the Anti conformer being 177.6^o compared to 174.2^o in the Gauche conformer.

Figure 6: Table showing the dihedral angles along the C(3)-C(4) bond in the two conformers

Atoms [Conformer]	Dihedral Angle
C(2)-C(3)-C(4)-C(5) [Anti 1]	-176.7o
H(10)-C(3)-C(4)-H(13) [Anti 1]	-178.1o
H(11)-C(3)-C(4)-H(12) [Anti 1]	-178.1o
C(2)-C(3)-C(4)-H(13) [Gauche 3]	171.1o
H(10)-C(3)-C(4)-H(12) [Gauche 3]	-178.7o
C(5)-C(4)-C(3)-H(11) [Gauche 3]	-172.8o

It is also worth inspecting the Van der Waals dispersion energy of the two conformers to see if this sheds any light on their relative stabilities. The distance at which there is the maximum attraction between two nuclei is the sum of their respective Van der Waals radii, therefore for hydrogen atoms, this attractive distance is approximately in the range 2.4-2.6 Å. Below in figure 7 is a table showing the attractive H^...H contacts around the C(3)-C(4) bond.

Figure 6: Table showing the dihedral angles along the C(3)-C(4) bond in the two conformers

Hydrogen Atoms [Conformer]	Distance / Å
H(8)...H(10) [Anti 1]	2.46
H(9)...H(11) [Anti 1]	2.56
H(10)...H(12) [Anti 1]	2.51
H(11)...H(13) [Anti 1]	2.52
H(8)...H(10) [Gauche 3]	2.47
H(9)...H(11) [Gauche 3]	2.55
H(10)...H(13) [Gauche 3]	2.54
H(11)...H(12) [Gauche 3]	2.50
H(11)...H(13) [Gauche 3]	2.41

This data seems to suggest that the Van der Waals dispersion energy slightly favours the Gauche 3 conformer as there are 5 attractive interactions around the gauche linkage compared with 4 attractive interactions around the anti-periplanar linkage. However, this effect is generally very small (in butane the Van der Waals dispersion energy favours the gauche conformer but only by ~0.27 kcal/mol), and as this analysis is merely qualitative, no definitive conclusion can be gathered from this data.

Optimising the Chair and Boat Conformations

Chair Transition State

Figure 1

C2h Chair Transition State	Cope Rearrangement

For this section, a CH₂CHCH₂ allyl fragment was drawn and then optimsied using the HF/3-21G method and basis set. The fragment was then copied and pasted twice into a new window, with the two fragments being placed in an approximate chair geometry with the terminal carbon atoms being ~2.2 Å apart. A Gaussian optimisation calculation for a transition state was then set up at the HF-3-21G level of theory. The calculation was set up as an Opt+freq calculation with the optimisation to a minimum tab changed to optimisation to a TS (Berny). The force constants were calculated once and Opt=NoEigen was added in the "Additional Keywords" box in order to stop the calculation crashing if more than one imaginary frequency is detected.

From this calculation an imaginary frequency at -818 cm^-1 was indeed obtained as stated in the script. This imaginary vibration corresponds to the Cope rearrangement which can be seen in figure 1 by clicking on the image (the Jmol of the chair transition structure from this calculation can be seen in figure 2).

Figure 2	Figure 3
Chair Transition Structure Part B	Chair Transition Structure Part D

After this, the original estimation of the chair transition structure was once again pasted into a new window, and the terminal carbon atoms were set an internuclear distance of exactly 2.2 Å using the Redundant Coord Editor. An optimisation calculation was then set up as if the structure were a minimum, using HF/3-21G method and basis set and with Opt=ModRedundant in the additional keywords.

Once the calculation was complete, the chk file was opened, and then the process was repeated except this time a transition state optimisation calculation was set up, and instead of calculating the force constants, a normal guess Hessian was used , modified to include the information about the bond coordinated that are being differentiated along (the Jmol from this calculation can be seen in figure 3).

A comparison of the carbon bond forming/bond breaking internuclear distances can be seen in figure 4 below.

Figure 4

Chair Transition Structure	C-C bond forming/bond breaking internuclear distance 1 / Å	C-C bond forming/bond breaking internuclear distance 2 / Å
From Initial Freq+Opt Calculation	2.0204	2.0204
From Frozen Coordinate Method	2.0199	2.0199

Interestingly, it can be seen that the C-C bond forming/breaking distance in the chair transition structure is calculated by the frozen coordinate method to be 0.0005 Å shorter.

A summary of the total energies of the optimised chair transition states can be seen below in figure 5 (but this information is tabulated later along with the data from the boat calculations in the activation energy section).

Figure 5: Table summarising the

Method and Basis Set	Total Energy/Hartrees
HF/3-21G	-231.55407
DFT B3LYP/6-31G*	-234.55407

Boat Transition State

Figure 1: Image showing the numbering of the reactant and product from the Cope Rearrangement

In order to analyse the boat transition state, a DFT B3LYP/6-31G (d) Freq + Opt QST2 calculation was set up. However, first the reactant and products were numbered to represent the Cope rearrangement as shown in figure 1.

When the calculation is set to run, it interpolates between the reactant and product to find a transition state. However, in this instance the calculation failed and rendered a structure representative of the chair transition structure as shown here: . This is because the calculation simply translated the allyl fragments and did not consider the rotation of the central C-C bonds.

Therefore, another QST2 calculation was set up, however, this time the geometries of the reactants and products were changed so that their geometries were closer to the boat transition structure. For both molecules, the dihedral angle for the central four carbons was changed to 0^o, and then the C(2)-C(3)-C(4) and the C(3)-C(4)-C(5) bond angles in the reactant molecule were changed to 100^o, with the same being done to the corresponding bond angles in the product molecule. The calculation was then run again at first using the HF/3-21G method and basis set, and then using the DFT B3LYP method and 6-31G* basis set; the Jmols and results can be seen in figure 2 below:

Figure 2: Table showing the results from the optimisation calculations of the boat transition structure

	HF/3-21G QST2						B3LYP/6-31G (d) QST2
Transition State	Electronic energy/ Hartrees	Sum of electronic and zero-point energies (0K)/ Hartrees	Sum of electronic and thermal energies (298.15K)/ Hartrees	Sum of electronic and thermal enthalpies (298.15K)/ Hartrees	Sum of electronic and thermal free energies (298.15K)/ Hartrees	Jmol	Electronic energy/ Hartrees	Sum of electronic and zero-point energies (0K)/ Harteres	Sum of electronic and thermal energies (298.15K)/ Hartrees	Sum of electronic and thermal enthalpies (298.15K)/ Hartrees	Sum of electronic and thermal free energies (298.15K)/ Hartrees	Jmol
Boat	-231.60280	-231.45091	-231.44528	-231.44433	-231.47911		-234.54309	-234.40234	-234.39600	-234.39506	-234.43109

Figure 3: Image showing Boat Transition State from the B3LYP/6-31G* QST2 calculation

As well as the calculated energies changing from the HF/3-21G calculation to the DFT B3LYP/6-31G* calculation, the stretching frequency of the imaginary vibration also changed from 841 cm^-1 from the HF method to 531 cm^-1 from the DFT method. The imaginary stretching frequency of the boat transition structure from the DFT calculation can be seen in figure 3.

It is also worth noting that upon comparison of the total energies of the two transition structures at both levels of theory, the chair transition structure is more stable, as expected.

Intrinsic Reaction Coordinate Method

Chair Transition Structure

From looking at the optimised chair and boat structures, it is very difficult to predict which 1,5-hexadiene conformers the transition structures connect. Therefore, in this section the Intrinsic Reaction Coordinate method is used. This method follows the minimum energy path from a transition structure to the nearest energy well, i.e. one of the connecting 1,5-hexadiene conformers. The method works by changing the geometry of the structure at a series of points along a steep section of the potential energy curve.

Therefore, the IRC method was used on the HF/3-21G optimised chair structure, computing at 50 points and only in the forward direction as the reaction coordinate is symmetrical. The link to the summary for this for this calculation can be seen here: link to summary, and the results can be seen below in figure 1:

Figure 1

Starting Structure	Graph showing the Total Energy along the IRC Reaction Coordinate	Graph showing the RMS Gradient Norm along the IRC Reaction Coordinate	Jmol	Energy of Product/ Hartrees	Conformation of the Product
Chair				-231.68514	Gauche 2

However, from looking at the RMS Gradient Norm graph, it can be seen that the product has not fully converged and so another calculation was run, this time computing the force constants at every step, not just once. The link to the summary for this for this calculation can be seen here: Link to calculation summary, and the results can be seen below in figure 2:

Figure 2

Starting Structure	Graph showing the Total Energy along the IRC Reaction Coordinate	Graph showing the RMS Gradient Norm along the IRC Reaction Coordinate	Jmol	Energy of Product/ Hartrees	Conformation of the Product
Chair				-231.68303	Gauche 2

It can now be seen that the product has in fact converged, and it resembles the Gauche 2 conformer. On top of this, the energy (-231.69166 a.u.) is very similar to the energy of the Gauche 2 conformer (-231.69167 a.u.) optimised using the HF/3-21G method and basis set earlier, giving further evidence that the chair transition state does in fact give the Gauche 2 conformer.

The Boat Transition Structure

This process was then repeated for the boat transition state, the results are shown below in figure 3.

Figure 3

Starting Structure	Graph showing the Total Energy along the IRC Reaction Coordinate	Graph showing the RMS Gradient Norm along the IRC Reaction Coordinate	Jmol	Energy of Product/ Hartrees	Conformation of the Product
Boat				-231.69266	Gauche 3

After the IRC calculation had finished, the resulting conformer was cleaned and re-optimised using the HF/3-21G method and basis set. The resulting conformer was Gauche 3.

Activation Energies

In order to calculate the activation energy for the Cope rearrangement, several factors had to be considered. For one the lowest energy conformer at each level of theory is chosen, therefore the energy of the Gauche 3 conformer is used for the reactant energy when using the HF/3-21G level of theory, and the Anti 1 conformer is used as the reactant when using the DFT B3LYP/6-31G* level of theory. However, this could lead to some discrepancies between the experimental values and the calculated values for the activation energy, as there would undoubtedly be a mixture of conformers in the laboratory, but this has not been considered here. The results from the calculations have been sumarised below in figure 1:

Figure 2: Table showing the relative energies of three chosen conformers after DFT B3LYP/6-31G (d) Frequency calculations

	HF/3-21G				B3LYP/6-31G (d)
Transition State	Electronic energy/ Hartrees	Reactant Conformer (Electronic Energy)/ Hartrees	Activation Energy/ Hartrees	Activation Energy/ kcal/mol	Electronic energy/ Hartrees	Reactant Conformer (Electronic Energy)/ Hartrees	Activation Energy/ Hartrees	Activation Energy/ kcal/mol	Experimental Value/ kcal/mol
Chair	-231.61932	Gauche 3 (-231.69266)	0.07334	46.0	-234.55407	Anti 1 (-234.61179)	0.05772	36.2	33.5±0.5
Boat	-231.60280	Gauche 3 (-231.69266)	0.08986	56.4	-234.54309	Anti 1 (-234.61179)	0.06870	43.1	44.7±2.0

It can be seen from the results that the calculated activation energies for the reaction are not very comparable to the experimental values when calculated using the Hartree Fock level of theory. However, when using the DFT B3LYP/6-31G* method and basis set, the calculated activation energy for the rearrangement reaction via the boat transition state agrees with the experimental value, and there is only a small discrepancy from the calculated E_A value for the chair transition state. Links to the log files from the calculation are listed below:

Link to log file for the HF optimised chair transition structure.

Link to log file for the DFT optimised chair transition structure.

Link to log file for the HF optimised boat transition structure.

Link to log file for the DFT optimised boat transition structure.

The Diels Alder Cycloaddition

Cycloaddition of Ethene and Cyclohexene

MO Analysis

Figure 1: [4s + 2s] Diels Alder Cycloaddition Reaction

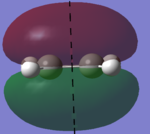
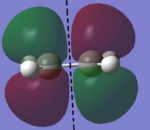
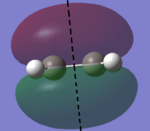
In this section, the [4s + 2s] Diels Alder cycloaddition reaction between ethene and cyclohexene is investigated (the reaction is shown in figure 1, right). As this reaction is only allowed if there is sufficient electron density overlap between the appropriate molecular orbitals, i.e., if the interacting orbitals are either both symmetric or antisymmetric in respect to a plane of symmetry, the HOMOs and LUMOs of cic butadiene and ethylene have been investigated, with the results being shown in figures 2 and 3 below (a=antisymmetric and s=symmetric):

Figure 2: Cis butadiene

AM1 HOMO (a)	AM1 LUMO (s)	DFT B3LYP-6-31G* HOMO (a)	DFT B3LYP-6-31G* LUMO (s)

Figure 3: Ethylene

AM1 HOMO (s)	AM1 LUMO (a)	DFT B3LYP-6-31G* HOMO (s)	DFT B3LYP-6-31G* LUMO (a)

As it can be seen below, the HOMO of ethylene and the LUMO of cis butadiene are both symmetric, and the HOMO of cis butadiene and the LUMO of ethylene are both asymmetric, meaning these pairs of orbitals can interact, allowing the reaction to take palce. Therefore, the transition state for the reaction was investigated.

It is also worth noting that these calculations were done at a higher level of theory also, but the same molecular orbitals were yielded meaning that AM1 is probably a sufficient level of theory.

The Transition State

Semi-Empirical AM1 Frequency Optimisation

Figure 1: Imaginary Vibration	Figure 2: Transition State
Figure 1: Imaginary frequency from the initial frequency optimisation calculation of the transition state	Calculated Transition State

In order to investigate the transition state from the Diels Alder reaction between cis-butadiene and ethylene, the two molecules were copied and pasted into the same window and the terminal carbons were orientated so that they were approximately 2 Å apart. A frequency optimisation calculation was then set up, calculating towards a Berny transition state, only calculating the force constants once. This calculation yielded the first approximation for the transition state, with an imaginary frequency at -956 cm^-1 (shown in figure 1). The C-C bond forming distances were calculated to be 2.1195 and 2.1194 Å from this calculation, and so this information was used to set up a more accurate transition state calculation using the frozen coordinates method, shown in the next section.

Frozen Coordinate Method

Next, the transition structure was optimised again, this time using the frozen coordinate method, freezing the C-C bond forming/breaking distance to 2.119 Å (this distance was chosen based on the results obtained from the initial calculation of the transition structure as described previously). This optimised the structure of the transition state, apart from the C(1)-C(6) and C(4)-C(5) bonds (as shown in figure 1). Therefore, the structure was optimised again, but this time using a normal guess Hessian modified to include the information about the bonds, along which the calculation will differentiate. The link to the log file for this calculation can be seen here: link to the log file for the Opt+Freq calculation , and the results can be seen below.

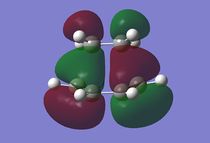
Figure 1: Numbered Transition State	Figure 2: Imaginary Vibration (-957 cm-1)	Figure 3: HOMO of the Transition State (a)	Figure 4: LUMO of the Transition State (s)

Figure 5: IR Spectrum from the Transition State

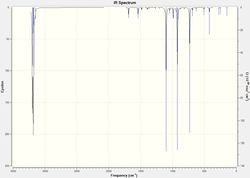
Figure 2 shows the only imaginary vibration obtained, the lowest positive vibration being 147 cm^-1 as shown in figure 5. This suggests that the reaction is concerted, therefore meaning the formation of the two bonds is indeed synchronous.

From figures 3 and 4 it can be seen that the HOMO is anti-symmetric and the LUMO is symmetric and that by comparing them to the HOMO and LUMO orbitals from the cis-butadiene and ethene molecules, it can be seen that the HOMO for the transition state is a mixture of the HOMO from cis-butadiene and the LUMO from ethene, and the LUMO from the transition state is a mixture of the LUMO from butadiene and the HOMO from ethene. This also makes sense as the symmetry of the orbitals will have been preserved, meaning the reaction is allowed.

Figure 6: Table showing all the C-C bond lengths of the Transition State (Geometry is C_s)

C-C bond	Internuclear distance / Å
C(1)-C(2)	1.38196
C(2)-C(3)	1.39648
C(3)-C(4)	1.38196
C(4)-C(5)	2.11900
C(5)-C(6)	1.38408
C(6)-C(1)	2.11900

The average C-C bond length for sp² hybridised carbon atoms is ~1.36 Å, and for sp³ hybridised carbons it is ~1.54 Å. From figure 6 the bond lengths shown in the calculated transition state suggest that all the C-C bonds in the butadiene molecule are a similar length, slightly greater than the average C-C bond length for the sp² hybridised carbon atoms. This suggests that there is a mixture of single and double bond character, with the C(2)-C(3) bond having slightly more single bond character at that stage of the reaction. The forming bonds between C(4)-C(5) and C(1)-C(6) are still fairly long and are actually in a repulsive Van der Waals radius distance (the attractive Van der Waals interaction distance for two carbon atoms in an organic molecule is ~3.2 Å). Hence, the structure being in a transition state.

Maleic Anhydride

Figure 1: Mechanism of the Reaction between Cyclohexa-1,3-diene and Maleic Anhydride

Figure 2: Endo Transition State	Figure 3: Exo Transition State
Endo Transition State	Exo Transition State

In order to calculate the endo and exo transition states of the Diels-Alder reaction between cyclohexa-1,3-diene and maleic anhydride (figure 1 above), the frozen coordinates method was used once again at the AM1 level of theory. The bond forming/breaking distance was set to 1.9 Å, and in order to reach the two different transition states the two molecules were simply orientated in approximately the right position to represent the transition state. The log files from the calculations can be seen here: log file for the endo transition state, log file from the exo transition state.

The Jmols from the calculation can be seen in figures 2 and 3, and the results from the optimisation of the transition states can be seen below.

Figure 4

Transition Structure	C-C bond forming/bond breaking internuclear distance 1 / Å	C-C bond forming/bond breaking internuclear distance 2 / Å	Total Energy / Hartrees	Total Energy / kcal/mol
Endo	2.16	2.16	-0.05150	-32.3
Exo	2.83	2.83	-0.05042	-31.6

Figure 5: Numbered Endo Transition State	Figure 6: Numbered Exo Transition State

From figure 4, the bond forming distances for the two transition states can be seen to be markedly different (these bonds are highlighted as being red in figure 1) as they have been calculated to be ~0.67 Å longer in the exo transition state. It can also be seen that the total energy of the exo transition state is ~0.6kcal mol^-1 higher in energy than the endo transition state. This result was expected however as the reaction is known to be under kinetic control with the endo product being preferred as stated in the literature. Some possible explanations for this can be seen below, as the Van der Waals dispersion energy is investigated, as well as some of the molecular orbitals of the two transition states.

Figure 7: Table showing some of the C-C interspace distances between the carbon atoms of the -(C=O)-O-(C=O)- fragment and the opposite carbon atoms (numbers refer to figures 5 & 6)

Carbon atoms (Transition Structure)	C-C bond distance / Å
C(1)-C(12) (Endo)	2.89
C(13)-C(14) (Endo)	2.89
C(9)-C(18) (Exo)	2.95
C(12)-C(15) (Exo)	2.95

As the attractive distance for C^...C inter-nuclear (through space) distance in organic molecules is ~3.2 Å, these results actually suggest that the exo transition state is energetically favoured by the Van der Waals dispersion energy. The endo carbon atoms in the endo product are ~2.89 Å apart, meaning they may be entering a repulsive distance, and if not, the attractive forces between them will have diminished to a greater extent than in the exo transition state. Therefore, as these results did not appear to shed light on the relative stability of the endo transition state, the MOs of the two structures were analysed in order to investigate any secondary orbital overlap.

Figure 8: Molecular Orbitals from the Two Transition Structures

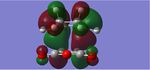
HOMO -18 (Endo)	HOMO (Endo)	LUMO +2 (Endo)	HOMO -18 (Exo)	HOMO (Exo)	LUMO +2 (Exo)

From looking qualitatively at the MOs of the two transition states, two molecular orbitals were found in the endo product that could possibly contribute to secondary orbital overlap and therefore stabilise the endo transition state. These same orbitals were then compared to the equivalent molecular orbitals in the exo product, where it can be seen that no stabilising MOs seem to be present in fact some nodes can be seen between the two joining molecules, perhaps contributing to the extra strain felt in the exo transition state, i.e. potentially explaining the energetic stability of the endo transition structure. However, these orbitals were found at the HOMO-18 and LUMO +2 eenrgy levels, the former being very low in energy and the latter relatively high. As the majority of the chemistry is dominated by the HOMO and LUMO orbitals, it is difficult to anticipate the contributions of these orbitals to the overall stability of the transition state. Therefore, the HOMOs of the two transition states were investigated (as shown in figure 8) however, there did not appear to be any secondary orbital overlap interactions, in fact, there were some nodes present in between the cyclohexa-1,3-diene and maleic anhydride molecules, perhaps meaning that a higher level of theory is needed in order to investigate fully the relative energies of the two transition structures.