Rep:Mod:gf609mod1

The Basic Techniques of Molecular Mechanics and Semi-empirical Molecular Orbital Methods for Structural and Spectroscopic Methods By Giovanna Fateh-Iravani

Modelling using Molecular Mechanics

Introduction

Molecular Mechanics is the use of non-quantum mechanical models to express molecular properties. It assumes that the total energy of a molecular system consists of the following:

• Stretch: The sum of all diatomic bond stretches, expressed by a Hookes law potential
• Bend: The sum of all triatomic bond angle deformations, expressed by a Hookes law potential
• Stretch-Bend: A correction that takes account of the coupling between stretching and bending
• Torsion: The sum of all tetra-atomic bond torsions, dependent on the cosine angle
• Van der Waals: The sum of all non-bonded Van der Waals repulsions, using a Lennard Jones potential
• Dipole-dipole: The sum of all electrostatic attractions of individual bond dipoles

The molecular mechanics attempts to minimise the total energy by adjusting bond lengths, bond angles and torsion angles to give the optimised molecular geometry of a conformation. Favourable interactions are shown as negative values. Allinger MM2 model implemented in ChemBio3D program will be used.

Diels Alder

Diels alder reactions are an example of a pericyclic reaction between a conjugated diene and a dienophile. The mechanism involves an aromatic transition state with six delocalized π electrons which leads to a stereo specific product.

An example of a Diels Alder 4πs + 2πs cycloaddition reaction is the dimerisation of cylopentadiene forming a norbene system. In this reaction two diastereoisomers are formed under different conditions.

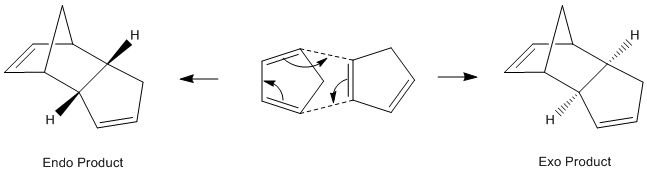
In Literature Baldwin states that the endo isomer is formed preferentially, but at higher temperatures and therefore thermodynamic control, it can be converted to the exo product. The minimum energy conformation was found by molecular modelling and the results were tabulated below:

Relative Energies (MM2) of the Cyclopentadiene Dimers

Energy in (kcal/mol)
	Exo Product	Endo Product
Stretch	1.2846	1.2507
Bend	20.5799	20.8476
Stretch-Bend	-0.8377	-0.8356
Torsion	7.6545	9.5107
Non-1,4 VDW	-1.4156	-1.5428
1,4 VDW	4.2333	4.3193
Dipole/Dipole	0.3775	0.4476
Total Energy	31.8765	33.9975
	Total Difference	2.1210

1,4 strain found in the Endo product explaining why the exo product is the more thermodynamically stable product

Under thermodynamic control, although the kinetic product is formed initially, it reverts back to the starting material due to the sufficient energy in the system and so eventually the thermodynamic product dominates. The Exo product is thermodynamically favoured since the 1,4 strain that is present in the endo product is not found in the exo product. The Exo product is therefore less sterically hindered and lower in energy as shown from the results above. The main difference in energy is the Torsion interactions. In the Endo product the Hydrogens are forced closer together and leads to unfavourable interactions. This steric clash means the Endo product has a higher overall energy under these conditions.

The Endo Transition State with stabilising interaction between frontier orbitals

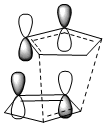
Under Kinetic control there is little thermal energy so the reaction is irreversible. The product with the lower transition state barrier dominates as less energy is required to surmount the barrier and the product with the faster rate of reaction is favoured. In the Diels Alder reaction the Endo product transition state has a through space bonding interaction between the dienophile and the developing π bond at the back of the diene. This stabilising interaction is due to the correct symmetry of HOMO and LUMO frontier orbitals. The Endo transition state is lower in energy than that of the Exo transition state and it is therefore kinetically favoured.

The Hydrogenation of Cyclopentadiene Dimer

From the results shown in the table below it can be seen that Structure 4 has a lower overall energy and is therefore the thermodynamic product. The transition state energy is unknown for both structures so it is unclear which structure is the kinetic product. Structure 4 has lower bending interaction and 1,4 Van der Waals interactions compared to Structure 3 and these more favourable interactions overcome the less favourable torsion interaction in Structure 4.

Relative Energies (MM2) of the Hydrogenated Products

Energy in (kcal/mol)
	Structure 3	Structure 4
Stretch	1.2780	1.0979
Bend	19.8658	14.5234
Stretch-Bend	-0.8349	-0.5496
Torsion	10.8068	12.4975
Non-1,4 VDW	-1.2257	-1.0693
1,4 VDW	5.6330	4.5114
Dipole/Dipole	0.1621	0.1406
Total Energy	35.6850	31.1520
	Total Difference	4.533

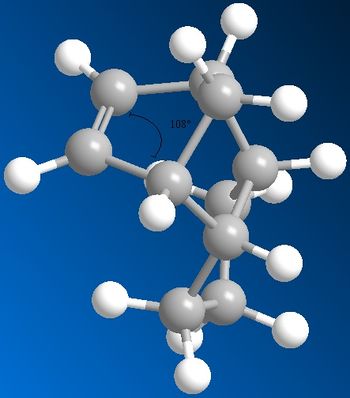
Angular strain is increased as the deviation from the ideal angle increases. Structure 3 has a sp2 bond which ideally would have a geometric angle of 120˚. From modelling it has a angle of 108˚ so a relatively large deviation. Structure 4 has a sp3 bond which modelling shows to be 102˚ this deviation is smaller from the ideal value of 109.5˚ compared to Structure 3. Therefore Structure 4 has less angular strain and so is the most stable product.

The sp2 angle of Structure 3

The sp3 angle of Structure 4

Structure 3 also has a double bond which fixes the hydrogen atoms in a geometry that gives unfavourable Van der Waals interactions with the adjacent hydrogen's. In structure 4 this double bond is absent so these hydrogens are able to freely rotate which reduces the interaction. The double bond in structure 4 also fixes the geometry of the hydrogen's, however they are fixed into a favourable site away from adjacent atoms.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Introduction

Taxol is one of the most important organic molecules of today and is an anticancer compound from yew trees.ref clayden . An initial intermediate is used for the total sysnthesis of Taxol and two possible geometries of this intermediate are shown below. In Structure 9 the carbonyl group is pointing upwards in plane with the adjacent hydrogen's of the cyclohexane. In structure 10 the carbonyl group is pointing down. The compound exhibits atropisomerism where on standing it isomerises to the alternative intermediate isomer.

Taxol 9

Taxol 10

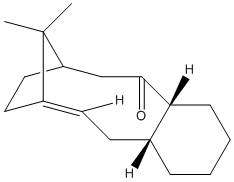MM2 and MMFF94 (Merck Molecular Force Field) energy values were calculated. MMFF94 is a method which uses different parameters to MM2 which have been derived from computational data. The cyclohexyl rings in the Taxol intermediates have two possible conformations, the twist boat and the chair; the chair is more energetically favoured. The table below shows the calculated energies for the two Structure 9 conformations and thwo Structure 10 conformations (one conformations and one twist boat conformation). It can be seen that Structure 10 chair conformation has the lowest energy and is therefore the most stable suggesting that the kinetic and initially formed structure is Structure 9 which on standing converts to the thermodynamic Structure 10.

Relative Energies (MM2 and MMFF94) of the different Taxol conformations

Energy in (kcal/mol)
	Taxol 9 Chair Conformation	Taxol 9 Twist Boat Conformation	Taxol 10 Chair Conformation	Taxol 10 Twist Boat Conformation
Stretch	2.7853	2.8069	2.6198	2.7074
Bend	16.5408	18.2312	11.3364	11.8273
Stretch-Bend	0.4311	0.4147	0.3432	0.3919
Torsion	18.2412	21.1534	19.6667	22.8862
Non-1,4 VDW	-1.5423	-1.3036	-2.1533	-1.9934
1,4 VDW	13.1079	14.7646	12.8724	14.3354
Dipole/Dipole	-1.7244	-1.6002	-2.0022	-1.9969
Total Energy	47.8397	54.4670	42.6830	48.1580
MMFF94	70.5509	76.4808	60.562	66.3285

It is stated that the alkene group in the Taxol intermediate reacts slowly and that the hydrogenated intermediates are less stable than Structures 9 and 10. MM2 and MMFF94 energy values were therefore calculated for the hydrogenated Structure 10 for comparison. The total energy values were found to be higher for the hydrogenated molecule than for Structure 10. The bridgehead alkene of Structure 10 is known as a hyperstable alkene which is less strained than the parent hydrocarbon, and therefore has decreased reactivity and increased stability.

Relative Energies (MM2 and MMFF94) of Hydorgenated Structure 10

Energy in (kcal/mol)
	Hydrogenated Structure 10
Stretch	5.3573
Bend	29.8786
Stretch-Bend	1.2040
Torsion	21.1601
Non-1,4 VDW	1.5635
1,4 VDW	19.7562
Dipole/Dipole	-1.7105
Total Energy	77.2056
MMFF94	115.812

The alkene strain energy can be calculated by subtracting the total energy of the alkane from the total energy of the alkene. This gives a negative value of -16.6436 kcalmol-1 for structure 10 which is mainly due to the torsion and Van der Waals components. When comparing the sp2 hybridised alkene angle and the sp3 hybridised alkane angle to ideal bond angles of 120˚ and 109.5˚ respectively, it is clear from the images below that there is a greater difference in the sp3 alkane bond angle suggesting that the alkane is less favourable and therefore the alkene is slow at reacting with electrophilic reagents.

Taxol 10 Alkane Angle

Taxol 10 Alkene Angle

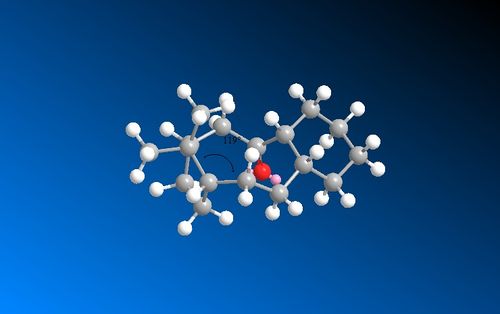As well as torsion strain there is also an added repulsive transannual H-H contact in the alkane which is not present in the alkene, due to a greater number of repulsive H-H Van der Waals interatctions in the alkane. This raises the alkane energy compared to the alkene and is another reason for the hyperstability of the alkene.

Modelling Using Semi-empirical Molecular Orbital Theory

Introduction

MOPAC will be used in this section for calculations as it is designed to implement semi-empirical quantum chemistry algorithms which take into consideration the orbital and electronic contributions of a molecule, which previous calculations above have not.

Regioselective Addition of Dichlorocarbene

Addition of Dichlorocarbene can occur at one of the two alkenes; either the endo alkene (below the chlorine) or the exo alkene (away from the chlorine). The MOPAC/PM6 calculations give a representation of the molecular orbitals of the molecule which will help to predict which alkene addition will occur at. Initially MM2 calculations were carried out to optimise the geometry, results of which are found in the table below:

Relative Energies (MM2 and MOPAC) of the Molecule 12

Energy in (kcal/mol)
	Molecule 12
Stretch	0.6193
Bend	4.7362
Stretch-Bend	0.0401
Torsion	7.6601
Non-1,4 VDW	5.7949
1,4 VDW	-1.0684
Dipole/Dipole	0.1123
Total Energy	17.8945
MOPAC Heat of Formation	19.7409 Kcal/Mol

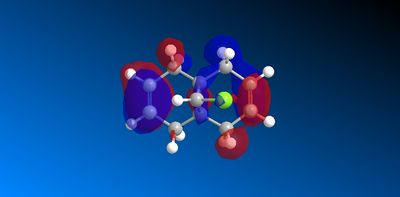
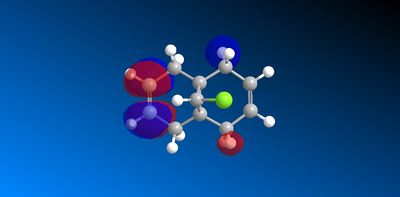
The molecular orbitals produced from the MOPAC/PM6 calculations are shown below:

HOMO-1 of Molecule 12	HOMO of Molecule 12
LUMO of Molecule 12	LUMO+1 of Molecule 12
LUMO+2 of Molecule 12

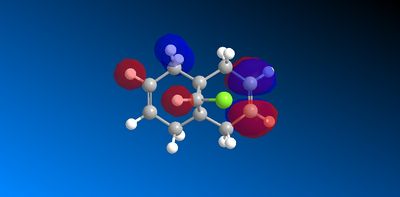The symmetry of the molecule is Cs with a unique σh plane of symmetry shown below, this is consistent with the plane of symmetry found in the molecular orbitals:

Plane of Symmetry of Molecule 12

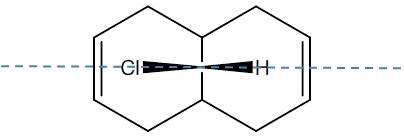
The HOMO has a lower overall orbital energy and greater bonding compared to the LUMO which is evident from the favourable and large interactions. It lies on the endo alkene where the greatest electron density is found. It is therefore the most reactive towards electrophilic attack and therefore addition reactions occur here over the exo alkene. It is also reported that the endo alkene is more nucleophilic than the exo since in the exo there is a stabilizing antiperiplanar orbital overlap between the C-Cl σ* orbital and the occupied exo π orbital. Electron donation from the exo alkene into the antibonding orbital is therefore feasible due to the high electronegativity of chlorine making the C-Clσ* bond low enough in energy for interactions. This results in the exo alkene becoming less electron dense and therefore less nucleophilic.

Relative Energies (MM2 and MOPAC) of the Molecule 12 Derivatives

Energy in (kcal/mol)
	Mono-ene	With OH Substituent	With CN Sunstituent>
Stretch	0.8975	0.6066	0.6453
Bend	4.6910	5.4372	4.5654
Stretch-Bend	0.0137	0.0306	0.0312
Torsion	10.7562	7.8008	7.4624
Non-1,4 VDW	-1.0632	-1.4390	-1.4261
1,4 VDW	6.9706	4.6918	6.7003
Dipole/Dipole	0.0708	-0.5589	-1.2741
Total Energy	22.3366	16.5691	16.7045
MOPAC/AM1	-2.431	000000	50.289

IR Frequency and Vibrational Energies

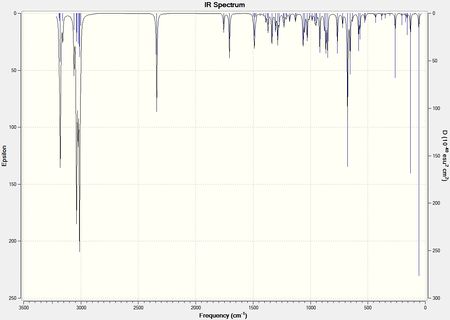
IR spectrums were predicted for the dialkene, monoalkene, CN substituted dialkene and the OH substituted dialkene:

IR of Molecule 12 Dialkene

IR of Hydrogenated Molecule 12 Monoalkene

IR of CN Substituent

IR of OH Substituent

The IR stretches were analysed in Gauss View, and the vibrations of bonds were looked at. The tabulated results show the stretches that will be focused on in the analysis:

IR Data for Dicarbene Derivatives

	C=CH Predicted Stretch (cm-1)	C-Cl Predicted Stretch (cm-1)	Exo C=C Predicted Stretch (cm-1)	Endo C=C Predicted Stretch (cm-1)
Dialkene	689.48	770.89	1737.26	1757.82
Monoalkene	673.81	774.97	-	1758.07
OH Substituent	677.32	743.74	1753.00 antisymmetric stretch of both alkenes	1757.76 symmetric stretch of both alkenes
CN Substituent	677.72	765.78	1706.27	1756

The results shown that in the monoalkene there is only one C=C stretching frequency corresponding to the endo double bond present which is as expected. The dialkenes exo C=C stretching is slightly lower than that of the endo. This is because electron density on the exo alkene is lost due to the LUMO+2/HOMO-1 interactions which weakens the double bond and therefore lowers yje stretching frequency.

The C-Cl stretching frequency is lower in the dialkene by 4.08cm-1 compared to the monoalkene. This is because the presence of the exo alkene donates electrons into the C-Clσ* orbital which weakens the C-Cl bond decreasing its stretching frequemcy.

When an electron withdrawing group such as CN was substituted onto the exo double bond, the stretching frequency of the C-Cl bond increased. This is because the CN removes electron from the alkene C=C bond reducing the density on the double bond. Therefore there is less donation from the alkene into the C-Clσ* so the C-Cl bond strength increases.

The opposite effect is seen when an electron donating group such as OH is substituted onto the exo alkene. The OH donates electron density into the double bond. Therefore there is increased donation from the double bond to the C-Clσ* orbital which decreases the C-Cl bond strength and the stretching frequency.

Monosaccharide Chemistry: Glycosidation

Introduction

A glycosidation reaction is when a nucleophile replaces a leaving group X on a sugar. The sugars shown below give different anomeric products which are dependent on the orientation of the neighbouring OAc group on the adjacent carbon.

D-glucose derivative

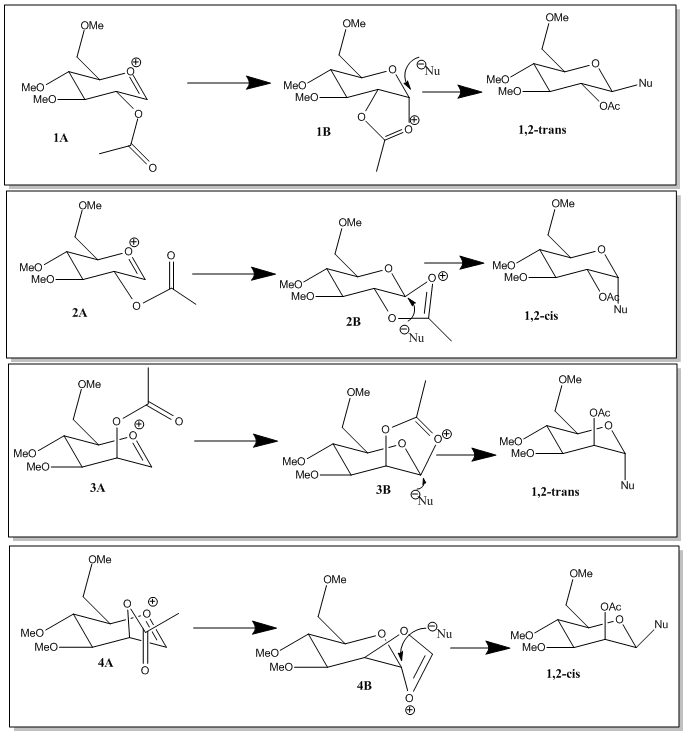
The oxonium cation intermediate is formed when the lone pair on the oxygen is pushed into the ring making X leave. When the intermediate oxoium cation is attacked from the bottom face by the acetyl oxygen, it blocks the bottom face and so the incoming nucleophile replaces it from the top forming the β-anomer. When the acetyl oxygen attacks from the top face, the incoming nucleophile replaces it from the bottom face forming the α-anomer. This makes the mechanism stereospecific.

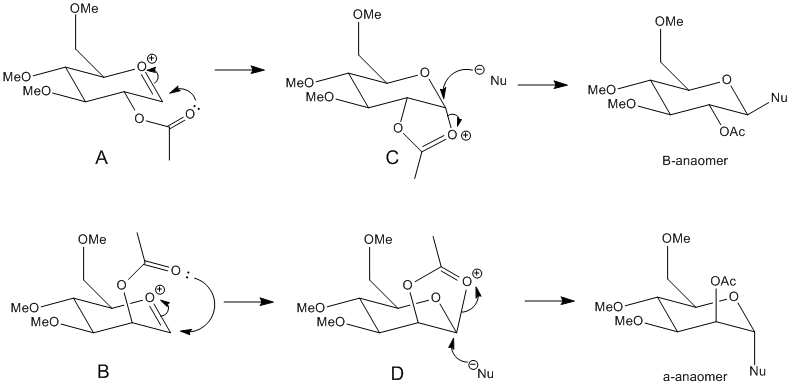
MM2 energies were calculated to optimise the geometries of A, B, C and D shown in the reaction scheme above, and then MOPAC/PM6 energies were calculated. MOPAC/PM6 calculations take into consideration orbital interactions and hydrogen bonding which the MM2 calculations do not. The main difference is that MOPAC/PM6 method thinks of a chemical bond as two electrons in an orbital instead of a rigid bond motif. This must be taken into account since the molecule is complex and contains heteroatoms. The R group that was used in the calculations was Methyl. This was chosen because it is small enough for calculations to be carried out efficiently in a given time. Hydrogen would have also been small enough, however it is not a protecting group and would give rise to added hydrogen bonding interactions.

The MM2 and MOPAC/PM6 energies are shown in the table below. A, B, C and D also have ring flipped isomer versions and so these energies were also calculated and are shown as A’,B’,C’ and D’. The two methods of calculating energies cannot be compared with each other since they take different parameters into consideration, however they are useful for showing a trend.

Relative Energies (MM2 and MOPAC) for Glycosidation

Energy in (kcal/mol)
	A MM2 A MOPAC	A' MM2 A' MOPAC	B MM2 B MOPAC	B' MM2 B' MOPAC	C MM2 C MOPAC	C' MM2 C' MOPAC	D MM2 D MOPAC	D' MM2 D' MOPAC
Stretch	2.6013	2.3805	2.6193	2.4769	1.9426	2.7949	1.7953	2.9613
Bend	11.6242	12.9009	15.1916	13.5854	12.7858	18.4873	17.6200	18.1804
Stretch-Bend	0.9771	1.0263	1.0723	0.9643	0.6404	0.8837	0.6943	0.8842
Torsion	3.2245	1.5450	1.2093	0.8173	8.0706	9.0707	8.0611	9.2348
Non-1,4 VDW	-0.5847	-3.1071	0.6242	-1.7798	-2.7614	-2.0815	-3.6667	-3.0271
1,4 VDW	18.8144	18.6500	17.9583	18.3943	18.1268	19.0520	17.9102	19.2305
Charge/Dipole	-16.2067	-0.0061	-19.7555	-3.3895	-8.7590	-0.3517	-4.8800	0.1245
Dipole/Dipole	8.3411	6.9794	8.2973	6.2458	-1.1296	-1.4455	-1.0566	-0.9781
Total Energy	28.7913	40.3689	27.2169	37.3146	28.9161	46.4100	36.4775	46.6106
MOPAC/PM6	-90.672	-68.334	-89.659	-66.234	-91.660	-66.881	-88.534	-66.726
Bond interaction distance (angstoms)	1.6	2.9	1.6	4.5	1.6	3.8	1.6	4.2
Angle of Attack (degrees)	104.8	15438	105.7	149.6	-	-	-	-

From the results tabulated it can be seen that the A and B are more stable than their corresponding ring flipped versions - A’ and B’. This is because the in A’ and B’ the carbonyl oxygen of the acetyl group is out of the plane therefore stabilizes the oxonium ion less than in A and B. Therefore the MM2 energies are higher for A’ and B’ and the MOPAC/PM6 energies are less negative ie less stable.

The results also show that A is more stable than B. This is because in A the carbonyl on the acetyl group interacting with the oxonium ion is orientated better to interact therefore the oxonium ion is stabilized better and so the energy is lower compared to B.

From the results C and C’ are lower in energy compared to D and D’. This is explained by the anomeric effect present in C and C’. Here you get stabilisation of the axial substituent since the lone pair from the oxygen in the ring is capable of donationating electrons into the correctly aligned C-Oσ* orbital. Therefore C and C' are more stable and so lower in energy.

Looking at the MOPAC/PM6 energies it can be seen that the energies of A and C are relatively similar and the energies of B and D are also very close in value. This is because MOPAC is capable of determining bonding interactions if the appropriate atoms are close enough in space. The same relationship is less evident in the MM2 energies as MM2 is not capable of this.

The distance between the δ+ carbon on the ring and the carbonyl oxygen were found after MOPAC/PM6 geometry minimisation using ChemBio3D. For A and B the bond distances were less than 2 angstroms which means that both are capable of forming neighbouring group interaction and can therefore stabilise the molecule.

The ring flipped structures A’ and B’ have a distance greater than 2 angstroms between the δ+ carbon on the ring and the carbonyl oxygen therefore there is no neighbouring group interaction to stabilise these structures. The structures are therefore unable to form conformations with the 107o Bürgi-Duntiz. The angles for A’ and B’ have a far greater deviation from this ideal angle than A and B explaining why A and B are more stable.

Mini Project: The Total Synthesis of (-)Cubebol

Introduction

The aim of this project is to show how computational methods of predicting and analysing molecules can be used to distinguish two isomeric products and give the most stable and likely product that will be formed in a synthetic pathway. The reaction pathway below shows the formation of (-)-Cubebol from (-)-Menthone. Many other Cubebol isomers can be formed however the (-)10-epi-cubebol isomer will be the focus of this project.

Cubebol is a natural sesquiterpene alcohol first found in cubeb oil. It has a unique property where it tastes cooling and refreshing.

The energies of all molecules were minimised via MM2 and MOPAC/AM1 methods and the results are tabulated below:

Relative Energies (MM2 and MOPAC) for Cubebol reaction

Energy in (kcal/mol)
	(-)-menthone (11)	Molecule 17	Molecule 18	(-)Cubebol	Isomer
Stretch	0.9088	9.9653	1.7857	1.9917	2.0407
Bend	2.1079	74.9425	8.7580	8.4106	8.4897
Stretch-Bend	0.2182	-1.3680	-0.5111	-0.4770	-0.4714
Torsion	7.9488	10.4314	18.8353	18.9947	19.4176
Non-1,4 VDW	-2.6108	-2.4992	-3.7914	-4.6315	-4.2360
1,4 VDW	7.4282	10.4317	8.8816	9.5013	-4.2360
Dipole/Dipole	-1.7110	0.1109	0.1001	0.1421	0.1456
Total Energy	14.2901	101.6383	34.0691	33.9319	35.0235
MOPAC/AM1	-80.299	-44.960	-71.43629	-74.566	-73.54437

From these predicted values Cubebol is the more thermodynamically favoured product compared to the (-)10-epi-cubebol isomer. This is shown by the more negative MOPAC/AM1 value and the lower MM2 energy, implying it is the more stable product.

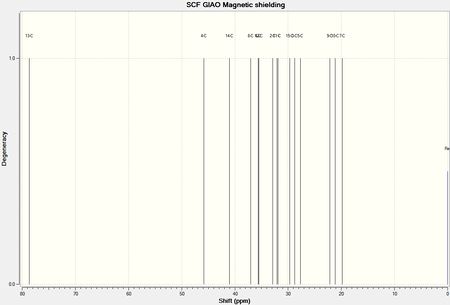
From the minimised geometries of the two isomers, the NMR spectrum, IR spectrum and Optical rotation were computationally predicted and are shown below. They are compared to literature values.

Cubebol NMR

Cubebol IR

Isomer NMR

Isomer IR

Numbered Carbons of Cubebol

Numbered Carbons of Isomer

NMR Data for Cubebol and Isomer

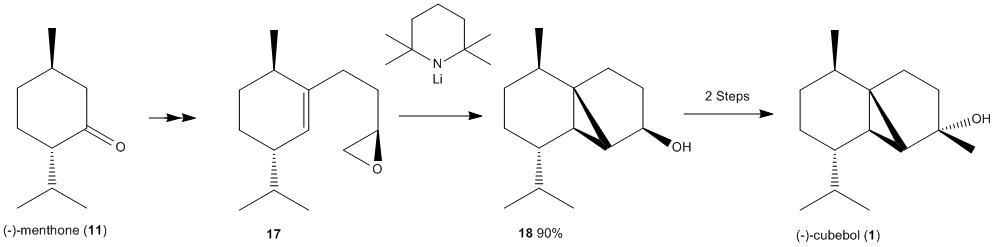
Carbon Label	Cubebol Predicted Resonance (ppm)	Cubebol Literature Resonance (ppm)	Difference (ppm)	Isomer Predicted Resonance (ppm)	Isomer Literature Resoncance (ppm)	Difference (ppm)
10	78.69	80.3	1.61	78.34	80.1	1.76
5	45.85	44.1	-1.75	44.93	42.4	-2.53
11	41.06	39.0	-2.06	43.12	41.1	-2.02
12	37.00	36.3	-0.70	36.82	36.5	-0.32
7	35.60	33.6	-2.00	35.70	33.7	-2.00
9	35.47	33.4	-2.07	35.34	32.8	-2.54
3	32.88	31.7	-1.18	33.14	30.8	-2.34
8	32.13	30.8	-1.33	31.08	29.3	-1.78
2	31.91	29.5	-2.41	30.89	29.3	-1.59
15	29.70	27.9	-1.80	29.78	28.6	-1.18
4	28.75	26.4	-2.35	26.01	20.7	-5.31
6	27.70	22.9	-4.8	23.88	19.9	-3.98
14	22.16	20.1	-2.06	22.19	19.7	-2.49
13	21.18	19.6	-1.58	21.12	19.2	-1.92
1	19.80	18.7	-1.1	19.18	17.4	-1.78

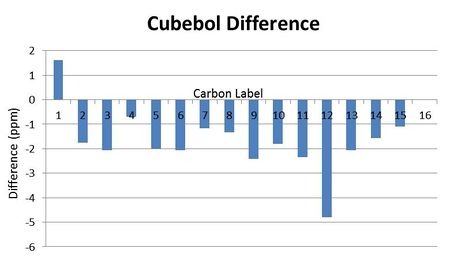
The NMR data is relatively close to that of literature for both isomers, which suggests that the computational predictions are relatively reliable since most fall within the NMR error range of ±5ppm. However there are not any obvious NMR values that can be used to distinguish the two isomers, which was the point of the spectrums. The greatest difference in values is for carbon 6 and carbon 4, however there is no particular reason why these should differ and the error range means these values may overlap regardless. H NMR would be an improved spectrum to predict however these are far more complex to calculate.

Bar charts were made for the difference between the literature values and the computationally predicted values. It is obvious that there is a systemmatic negative error in the results:

Bar Chart to show the deviation from literature values for Cubebol

Bar Chart to show the deviation from literature values for Isomer

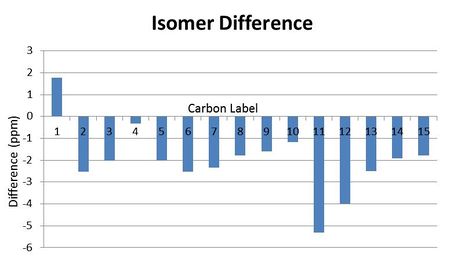IR data for the two isomers is shown below. From looking at the spectrum there is not any peak which is particularly different in the two so again it may be difficult to distinguish the two isomers from this. The main difference in the stretching frequencies is between the CH2 stretches, and this is a possibility for differentiating the two isomers. The CH2 in the molecules are the carbons labelled 3,4,8 and 9 found on both six membered rings. In the isomer both substituents in the first ring are in the same plane which may effect these CH2 groups by decreasing their vibrations since there is more steric bulk. This decrease in vibration would lead to a lower stretching frequencies compared to that of cubebol.

IR Data for Cubebol

	Cubebol Predicted Stretch (cm-1)	Cubebol Literature Stretch (cm-1)	Difference (cm-1)
OH Stretch	3802.2	3350	-452.2
CH Stretch	2953.5	2951	-2.0
CH Bend	1501.3	1490	-11.3
CH2	1151.7	1142	-9.7
CH	906.8	910	3.2

IR Data for the Isomer

	Isomer Predicted Stretch (cm-1)	Isomer Literature Stretch (cm-1)	Difference (cm-1)
OH Stretch	3800.6	3390	-410.6
CH Stretch	3025.8	2956	-69.8
CH Bend	1498.3	1447	-51.3
CH2	949.2	946	-3.2
CH	934.6	931	-3.6

The optical rotation for Cubebol was predicted to be -39.7 deg, this is slightly off that of literature at -48.3 deg, however both values are negative which shows that the direction in which light is polarised has been correctly predicted.

The optical rotation for the isomer was predicted to be -62.75 deg, this is slightly off that of literature at -72.3 deg, however they are both negative values which shows that the direction in which light is polarised is correct.

The optical rotation values are useful since they predict the direction in which light will be polarised correctly, however the numerical values are relatively inaccurate so may not be a very useful way to distinguish the two isomers. If the enantiomer of cubebol was investigated instead it would be expected to have a positive optical rotation value, so this technique would be more useful in this instance.

Conclusion

The data collected was reliable since it compared well to literature, however the spectrums would not be a good enough method to distinguish the two isomers.