Rep:Mod:gck12

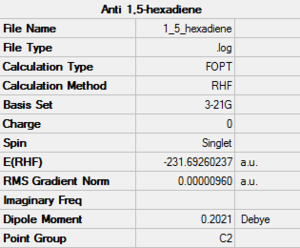
1,5-Hexadiene Hartree-Fock 3-21G Optimisation

summary data

Jmol

optimised 1,5-hexadiene

Point group: C2

The optimised molecule is found to be anti 1, from table 1.

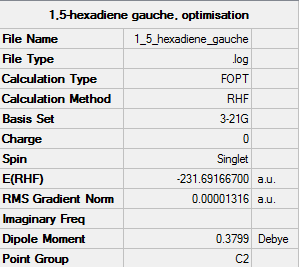
1,5-Hexadiene Hartree-Fock 3-21G gauche Optimisation

summary data

Jmol

optimised 1,5-hexadiene gauche

Point group: C2

The optimised molecule is found to be gauche 2, from table 1.

The anti arrangement gives places the C-C σ the neighboring C-C σ* orbitals at 180 degrees to each other and are anti-peri planar. This allows the two orbitals to interact and lowers the energy of the σ orbital and raises the energy of the σ*. Since only the bonding orbital between the two carbons are occupied, the anti molecule is stabilised by this orbital interaction. This is not possible in the gauche arrangement as the geometry of the two orbitals disfavor interactions.

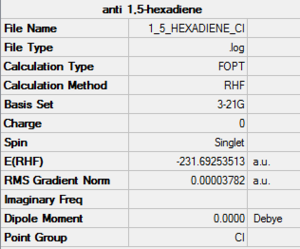
1,5-Hexadiene Hartree-Fock 3-21G gauche Optimisation, Ci symmetry

summary data

Jmol

optimised anti 1,5-hexadiene

The optimised 1,5-hexadiene molecule with a Ci symmetry and energy-231.69254 hartrees is the anti 2 molecule, found in table 1.

1,5-Hexadiene DFT B3LYP/6-31G gauche Optimisation, Ci symmetry

summary data

Jmol

optimised anti 1,5-hexadiene

A higher level of theory is used to optimise the anti 2 conformer. The energy value of the reactant will have to be found in order to calculate the activation energy of the Cope rearrangement. The DTF B3LYP 6-31G basis set will give more accurate energies than the Hartree-Fock 3-21G basis set as 6 functions are used to model the orbitals in 6-21G as opposed to 3 functions used in the 3-21G basis set (Besides core electrons, you also have more functions to describe valence electrons, and since you might have used the basis set 6-31G*, also represented by 6-31(d), you also include d orbitals for carbon atoms in order to allow for the polarization of its electronic density João (talk) 12:10, 24 March 2015 (UTC)). Furthermore DTF better represents exchange energy (Actually exchange treatment is exact in Hartree-Fock. João (talk) 12:10, 24 March 2015 (UTC)) and also include contribution from electron correlation.

Table 2. Comparison of HF/3-21G and B3LYP/6-31G Geometries for Anti 2 Conformation.
	C=C bond (pm)	C-C bond (pm)(carbon 3 and 4)	C=C-H angle
HF/3-21G	131.6	1.55.3	121.9
B3LYP/6-31G	133.8	155.5	121.7

Hartree-Fock gives shorter bond lengths, with DTF giving the sp3-sp2 carbon bond a bond angle closer to 120 degrees. (Is there a reason to expect an angle of exactly 120º? More generally are these structural differences significant? João (talk) 12:10, 24 March 2015 (UTC))

1,5-Hexadiene DFT B3LYP/6-31G frequency calculation

Table 3. Calculated Thermochemical Parameters of B3LYP/6-31G Optimised anti 2 1,5-Hexadiene.
Parameter	Calculation at 298.15K (Hartrees)	Calculation at 0.01K (Hartrees)
Sum of Electronic + Zero-point Energies	-234.401704	-234.40170
Sum of Electronic and Thermal Energies	-234.396081	-234.401702
Sum of Electronic and Thermal Enthalpies	-234.395137	-234.401702
Sum of Electronic and Thermal Free Energies	-234.430821	-234.401702

The frequency calculation was carried out at 298.15k and 0.01k at 1 atmospheric pressure. The energies carried out at 0.01K were of the same value as the thermal contribution was too small to have any significant effect on enthalpy and free energy.

(Besides thermochemistry data, is there any other reasons to perform frequency calculations? How do you know if the structures you found are minima on the potential energy surface? João (talk) 12:10, 24 March 2015 (UTC))

Optimising chair TS - Berny vs frozen coordinate method

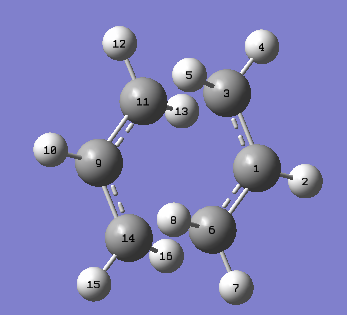
Chair TS of the Cope rearrangement

Two allyl fragment was optimised at the Hartree-Fock/3-21G level of theory. Force constants was calculated once. The Berny optimisation gave a chair transition state with the imaginary frequency at 818cm-1.

Table 4. Comparison of the geometries of the chair transition structure using berny and forzen coordinate method.
Atom Labels	Berny Optimisation (Å)	Frozen Coordinate Optimisation (Å)
C14-C6	2.02044	2.02045
C3-C11	2.02072	2.02067
H4-H12	2.63160	2.63199
H-H	2.43748	2.43728

(What do you conclude from your comparison of both methods? João (talk) 12:10, 24 March 2015 (UTC))

Optimising boat TS - QST2

Imaginary frequency is located at 840cm-1

Boat TS of the Cope rearrangement

IRC on chair transition structure

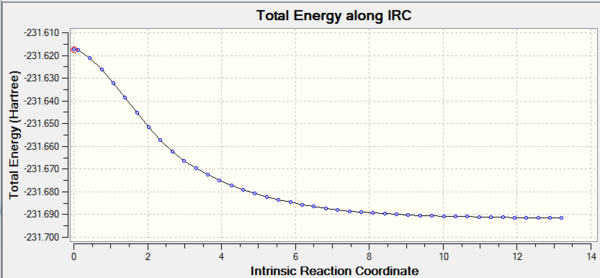
IRC is a method where the largest negative gradient is used to determine a local minima in the potential energy surface (PES) in a transition state (More than finding a local minimum, this method provides a reaction path connecting 2 local minima (reactants and products) via a transition state. João (talk) 12:10, 24 March 2015 (UTC)). The IRC calculation converged after 44 runs despite imputing 50 runs, which shows the local minima is reached. The energy on the PES was found to be -231.69157075 hartrees. (Which conformer is reached? João (talk) 12:10, 24 March 2015 (UTC))

Activation energy of the Cope rearrangement

Table 7. Energy values relevant for Activation Energy Calculations.
Structure	B3LYP/6-31G* Electronic Energy (Hartrees)	B3LYP/6-31G* Sum of Electronic and Thermal Energies at 0.01 K (Hartrees)	B3LYP/6-31G* Sum of Electronic and Thermal Energies at 298.15 K (Hartrees)
Chair	-234.556694	-234.414257	-234.408361
Boat	-234.55864039	-234.402258	-234.411999
Anti 2 Reactant	-234.55970472	-234.401702	-234.396081

Activation Energies Predicted by B3LYP/6-31G* Levels of Theory.
Pathway	B3LYP/6-31G* at 0.01 K (kcal/mol)	B3LYP/6-31G* at 298.15 K	Experimental at 0 K (kcal/mol)
Chair	34.07687891	33.18513657	33.5
Boat	41.95461468	41.32393576	44.7

(Do you still obtain a transition state at the higher level of theory? How do the transition state geometries compare at different levels of theory? Which is the more favorable transition state for the reaction? João (talk) 12:10, 24 March 2015 (UTC))

Diels-Alder Cycloaddition

Cis-Butadiene

The HOMO and LUMO of the reactant cis-butadiene were shown from the optimisation of the molecule using AM1 semi-empirical level of theory. The HOMO and LUMO of butadiene are anti-symmetric with respect to the plane of symmetry in the molecule, which bisects the central C-C bond. (span style="color:gray">Are they both anti-symmetric? João (talk) 12:10, 24 March 2015 (UTC))

Prototype Diels-Alder reaction

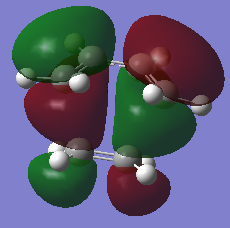
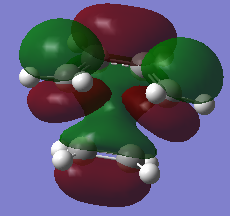
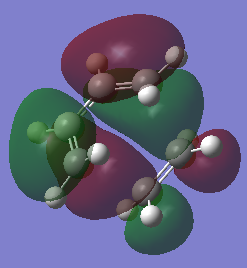
Imaginary frequency of the bond forming in the TS.

Diels-Alder TS

Table 9. Geometry of Diels-Alder Transition Structure with carcon numbered 1 to 6, with 1-6 and 4-5 being the partially formed carbon sigma bonds.
Atom Labels	Bond Lengths(Å)
C1-C2	1.38
C2-C3	1.40
C3-C4	1.38
C4-C5	2.12
C5-C6	1.38
C6-C1	2.12
H7-H15	2.60
H7-H6	2.55

The prototype Diels-Alder reaction in this case is the reaction of cis-butadiene with ethylene to give cyclohexene as the adduct. The HOMO and LUMO of the adduct (Do you mean adduct or transition state? João (talk) 12:10, 24 March 2015 (UTC)) is calculated from the AM1 semi-empirical level of theory. As seen from figurex the HOMO is found to be anti-symmetric with respect to the plane of symmetry, whereas the LUMO is determined to symmetric about the central carbon-carbon sigma bond.

Typical spЗ-spЗ carbon bond lengths, sp2-sp2 lengths and Van der Waals radii for a carbon atom is approximately 1.54Å, 1.34Å and 1.70Å respectively. The forming carbon-carbon bonds has a length of 2.12Å, which is within twice the Van de Waals radii. This shows there is an attractive interaction between the two forming carbon atoms, favoring bond formation. Figurex shows the imaginary frequency of the formation of the carbon-carbon sigma bond in the transition state is synchronous. The HOMO of the Diels-Alder adduct is anti-symmetric with respect to the plane of symmetry. A set of rules concerning the conservation of orbital symmetry formed by Woodward and Hoffmann is used to predict if a pericyclic reaction is allowed or not. the prototype reaction is a thermally allowed 4n+2 cycloaddition, with suprafacial rotation. the HOMO of cis-butadiene and LUMO of ethylene are on the same face of the fragment and are also in the same phase, which gives a favorable and low energy interaction. As a result the reaction is allowed.

Table 10. Activation Energy of Prototype Reaction.
Structure	AM1 Sum of Electronic and Thermal Energies at 298.15 K (Hartrees)	AM1 Activation Energy (kcal/mol)	B3LYP/6-31G Sum of Electronic and Thermal Energies at 298.15 K (Hartrees)	B3LYP/6-31G Activation Energy (kcal/mol)	Experimental (kcal/mol) ²²
Ethylene	0.080255	25.4938328	-78.539630	20.739193	27.5 (2)
Cis Butadiene	0.138571	25.4938328	-155.906508	20.739193	27.5 (2)
DA Transition State	0.259453	25.4938328	-234.413088	20.739193	27.5 (2)

Cycloaddition of cyclohexa-1,3-diene with maleic anhydride

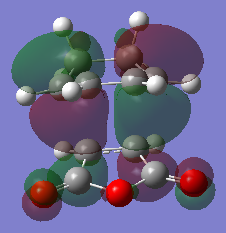
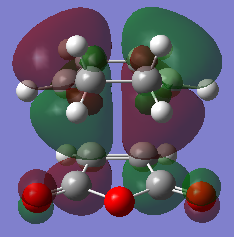
The exo and endo transition state was located at the AM1 level of theory. The imaginary frequency for the endo transition and exo transition state is 806cm-1 and 812cm-1 respectively with the oscillation of the bond forming carbons as proof of the transition state structure. The vibrations of the endo and exo product is synchronous. As seen in tableX, the forming C-C bond length is shorter in the endo transition structure than the forming C-C bond in the exo structure. This is due to the steric repulsion of bridging -CH2-CH2- group with the carbonyl-oxygen-carbonyl fragment as the two groups are comparable in size. Another contribution to the different bond lengths is from secondary orbital effects. Since the double bonds in the maleic andyhride and cyclohexadiene are placed directly above each other, the orbitals can overlap favorably to form sigma bonds. As orbitals from the double bond in cyclohexadiene overlap with orbitals in the carbonyl fragment, the diene will lose some double bond character. This is evident from the longer bond between C1 and C4 in the endo transition structure. It is this secondary orbital effect that result in the endo transition structure having a lower energy than the exo transition structure. Hence the endo product is normally formed first; giving the kinetic product. The exo product is "anti" to the largest cyclic bridge which in turn gives less steric strain and is the lower energy product, giving the thermodynamic product.

endo transition state

exo transition state

The endo transition state has been found to have a lower energy then the exo transition state, with a difference of 0.00108495 hartrees.

Absolute energy of exo TS(hartress): -0.05041985 hartrees

Absolute energy of endo TS(hartress): -0.05150480

Absolute relative energy(hartress): 0.00108495

Absolute relative energy(kcal/mol): 0.68081654923

Endo - sum of electronic and thermal Energies(hartrees)= 0.143683

Exo - sum of electronic and thermal Energies(hartrees)= 0.144881

Relative sum of electronic and thermal Energies(hartrees)= 0.001198

relative energy(kcal/mol): 0.75175651

Table x. geometry of endo and exo TS.
Atom Labels Exo	Bond Lengths (Å)	Atom Labels Endo	Bond Lengths (Å)
C3-C17	2.17040	C2-C17	2.16239
C2-C16	2.17040	C3-C16	2.16239
C1-C4	1.39676	C1-C4	1.39724
C3-C4	1.39438	C1-C2	1.39305
C16-C17	1.41011	C16-C17	1.40849
C12-C18	2.17048	C2-C8	2.16238
C12-C18	2.94508	C1-C18	2.89222

secondary orbital overlap effect?

The HOMO of the endo and exo transition state were plotted as shown in figureX and figurex. It is expected that secondary orbital effect will be observed in the HOMO of the endo Transition state. This is not the case for the plotted HOMO. There are no in-phase overlap between the carbonyl orbitals and the orbital from the double bond in cyclohexadiene. However seondary orbital effect is present in lower energy orbitals below the HOMO. (It would be worth showing that. João (talk) 12:10, 24 March 2015 (UTC))

AM1 neglected effects

The semi-empirical AM1 method has a few setbacks which effects the accuracy of the calculations. The AM1 greatly underestimates the barrier of bond rotation with partial double bond character and predicts alkyl groups to be more stable than reality (Reference? João (talk) 12:10, 24 March 2015 (UTC)). The calculated hydrogen bond strength is close to experimental results, but the geometry of the hydrogen bonds is often misrepresented. Van der Waals interactions are also poorly predicted. This could provide an explanation to why the secondary orbital effect is not observed in the HOMO of the endo transition structure.