Rep:Mod:gHoST wriTER
Module 1: Structure and Spectroscopy (Molecular Mechanics/Molecular Orbital Theory)
All Geometries/Energies are derived using the ChemBio3D Suite/MM2 Force Field, unless otherwise specified. Also, the methods used below do not account for kinetic control type structures, i.e. transition states, as they are unable to process these states without full knowledge of their geometries/energies already to optimize further.
Modelling using Molecular Mechanics
The Hydrogenation of Cyclopentadiene Dimer
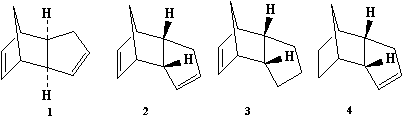
Cyclopentadiene readily dimerises at room temperature, where the structure of the dimer produced could be either 1 (exo) or 2 (endo). Specifically, the endo dimer 2 is produced.[1] Hydrogenation of this dimer produces one of the dihydro derivatives 3 or 4, at first, and after prolonged hydrogenation the tetrahydro derivative is produced.
To confirm whether the formation of endo dimer 2 is under thermodynamic or kinetic, the geometries of both dimers 1 and 2 have been optimised (minimising their energies):
 |
 |
Above are the optimised geometries of both dimers. The total energy of the exo dimer was found to be 31.8834 kcal mol-1, and that of the endo dimer was 34.0063 kcal mol-1. As can be seen from these energies, the exo dimer is lower in energy than the endo dimer, and hence it is the more stable product, and so would be expected to be formed under thermodynamic control. However, as has already been stated previously, the endo dimer is favoured in the dimerisation of cyclopentadiene; therefore, we can presume that the selective formation of this dimer is via kinetic control. This can be explained by the fact that the transition state leading to the formation of the endo dimer must be significantly lower in energy and more accessible than the corresponding one leading to the exo dimer. Unfortunately, we can't really understand this using the MM2 force field, as it is based on classical mechanics, and doesn't account for orbital interactions/stereoelectronic control using MO methods. The increased energy of the endo form can be attributed to the fact that the two Cp rings are "facing" each other (they are syn to each other), and so steric repulsion is increased (taking the hydrogen atoms attached to the rings into account) compared to the exo form.
The hydrogenation of the endo Cp dimer leads to initially two regioisomers, the dihydro derivatives 3 and 4. To decide which one of these is more stable as a product created under thermodynamic control, the geometries of both dihydro derivatives are optimised, and their total energies and the relative contributions to these energies are compared:
 |
 |
| Dihydro Derivative 3 | Dihydro Derivative 4 | |
|---|---|---|
| Stretch | 1.2348 | 1.0963 |
| Bend | 18.9596 | 14.5074 |
| Stretch-Bend | -0.7626 | -0.5493 |
| Torsion | 12.1205 | 12.4972 |
| Non-1,4 VDW | -1.5108 | -1.0507 |
| 1,4 VDW | 5.7300 | 4.5124 |
| Dipole-Dipole | 0.1630 | 0.1407 |
| Total Energy | 35.9346 | 31.1540 |
Looking at these energy values, we can see that thermodynamically, dihydro derivative 4 is more favoured in the hydrogenation of the endo dimer, with a lower total energy of 31.1540 kcal mol-1 compared to the total energy of 3 , 35.9346 kcal mol-1. This shows that the double bond located in the 6-membered ring with bridging methyl is easier to hydrogenate than the one in the unaltered 5-membered ring. A mutiple bond in a ring system confers some strain to the system, which usually increases with decreasing ring size; however, because of the bridge in the 6-membered ring, the double bond located in this ring is actually in a much more strained and higher energy system. Therefore, this double bond is more reactive and is more likely to react, producing the dihydro derivative 4. In comparing the relative contributions to these total energies, for most energy terms the value is slightly larger for the derivative 3 than for 4. More significantly, the Bend contribution is 4.4522 kcal mol-1 greater for 3 than for 4; this displays the significant strain found in the bridged 6-membered ring. Also, the Torsion contribution is lower for 3 than for 4, although perhaps insignificantly with a 0.3767 kcal mol-1 difference, going against the fact that dihydro derivative 3 is higher in energy overall than 4. The Stretch and 1,4 VDW (van der waals') contribution differences are smaller compared to the Bend contribution difference, although some significant difference is seen for the 1,4 VDW contribution (1.2176 kcal mol-1), and there is no hydrogen bonding term.
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
(Here using the MMFF94 force field for this section)
 |
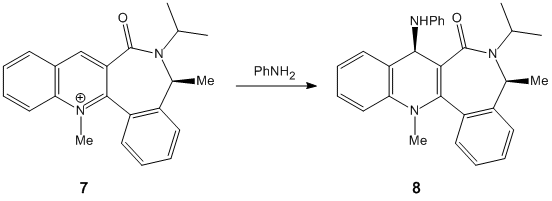 |
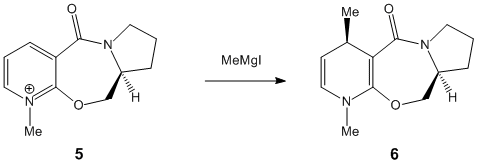
The nucleophilic additions to the pyridinium rings 5 and 7 (analogous to NAD+, a metabolic coenzyme) proceed to form products 6 and 8 respectively with the absolute stereochemistry shown above. The 5-->7 reaction involves methylating the pyridine ring of 5 at the 4-position using MeMgI (a Grignard reagent), and the 7-->8 reaction involves derivatising the pyridinium ring of 7 with aniline, again at the 4-position (which can then transfer the NHPhenyl group to other electrophiles). In studying these reactions, and the reactants 5 and 7 in particular, the stereocontrol which governs the reactions is deduced; this is done by optimising the geometries of both reactants, to see what the absolute stereochemistries of the most stable conformers of them is.
|
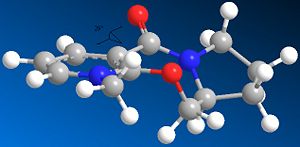 |
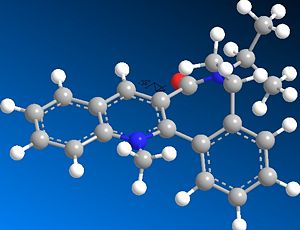
|
The optimisation was attempted for reactant 5 including the MeMgI Grignard component; however, it failed, as the ChemBio3D/MMFF94 force field could not recognise the Mg atom. This was because the software did not contain the necessary parameters needed to include the Mg atom in any optimisation. In optimising the geometry of both reactants, because they both contained a 7-membered ring which would be considered flexible (and a 5-membered ring in the case of reactant 5), several conformations were initially defined prior to optimisation. However, it was later found that this was not so, and in fact that for reactant 5 there were the only two significantly different conformers energy-wise (see below for energy values). Also, for reactant 7 there was only one significant conformer; in both reactants' cases, conformers/stereoisomers fitting the absolute stereochemistries defined (i.e. the wedged/hashed bonds shown in the original 2D structures) were only considered. Other conformers/stereoisomers were also found, but they were opposite in absolute stereochemistry at these chiral centres (also causing the orientation of the C=O to flip to the other side of the pyridinium plane; see below). The hindered flexibility of the 7-membered ring system can be attributed in particular to its adjoining phenyl groups in both 5 and more so in 7.
| Pyridinium reactant 5-lowest energy conformer | Pyridinium reactant 5-higher energy conformer | Pyridinium reactant 7-single conformer |
| 54.5047 | 60.7638 | 98.3656 |
Considering pyridinium reactant 5, the lowest energy and therefore more stable conformer is determined to be the correct optimised geometry (applying the variation principle here). Looking at both conformers, it is seen that the C=O moiety in both cases is orientated above the plane of the adjacent aromatic (pyridine ring); the dihedral angle is 19o for the lowest energy conformer, compared to 29o for the higher energy conformer. This suggests that the C=O somehow directs the stereocontrolled nucleophilic addition of the Me group; this is correct, as the oxygen atom of C=O coordinates to the -(+)MgI component (specifically the Mg atom), thus directing the nucleophilic addition of Me to occur above the plane of the pyridinium ring as well, forming the product 6 with its absolute stereochemistry. The C=O group is anti to the proton at the chiral centre in 5 mentioned previously, and this confirms how the absolute stereochemistry at this centre almost dictates the orientation of the carbonyl ring and the subsequent direction of delivery of the nucleophile/Me.[2]
Considering pyridinium reactant 7, the C=O group is this time below the plane of the pyridinium ring (dihedral angle = -38o). This implies that steric repulison controls the stereochemistry of the rather bulky aniline addition, and indeed diastereofacial selectivity dictates the direction of attack, as the aniline will approach to the face of the pyridinium ring opposite to where the C=O (and the oxygen atom's lone pairs) resides. This creates the product 8 with its absolute stereochemistry.[3]
One particular way of improving on the simple models created by the MMFF94 force field is to use a more advanced approach to modelling the molecules, rather than Molecular Modelling. This can be done using a Molecular Orbital/(Semi-)Quantum Mechanical approach such as MOPAC PM6 method instead. Unlike Molecular Modelling which only takes classical mechanical energy terms into account, PM6 takes into account stereoelectronics and orbital effects, and includes the frontier HOMO/LUMO orbital interactions, in trying to determine the paths reactions proceed by, and their stereochemistry.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
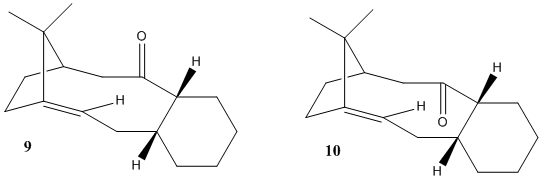
Atropisomerism is a class of stereoisomerism concerning isomers created as a result of hindered rotation about (central) single bonds, as the steric strain barrier to rotation is high, producing isolable conformations. These show axial chirality, which makes them a significant class of compounds. The above intermediates 9 and 10 in the synthesis of Taxol (an important drug for the treatment of ovarian cancers) are worthy examples of this type of isomerism; the single bond about which there is hindered rotation is the single C-C bond that is adjacent to the C=O bond but further away from the cyclohexyl group. Another good example of this type of isomerism is Vancomycin.[4]
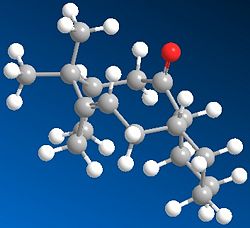
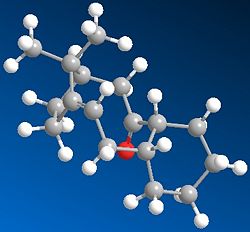
This key intermediate was initially synthesised as either 9 or 10, and then upon standing it isomerised to the alternative isomer. Here it is displaying a key feature of atropisomers, which is that they can interconvert with a thermal dependence, rather than via chemical means, as for most other chiral compounds. In order for one to predict what the stereochemistry of any product created as a result of addition at the carbonyl centre would be, the most stable isomer needs to be determined. Thus the geometries of 9 and 10 were optimised:
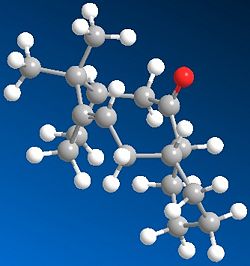
|
|
|

|
| 54.3915 | 48.9012 | 49.8887 | 44.2763 |
The first thing to notice here is that for each isomer 9 and 10, there are two different conformational types.[5] Upon defining the structures for both in ChemDraw and minimising their energies, one of the major stable conformations of the cyclohexyl group was produced (chair or twist-boat). Therefore it was decided to adjust the structure of the optimised geometry so as to produce the other conformation of the cyclohexyl group, and hence the other major conformation of the intermediate, to see which was lower in energy.
Comparing the energies of all conformations, it can be seen that Isomer 10 with chair cyclohexyl conformation is the most stable one, with an absolute energy of 44.2763 kcal mol-1. In both isomers' cases, the chair conformation is always more stable than the twist-boat by ~5.5kcal mol-1, reflecting the relative stabilities of chair and twist-boat cyclohexane. Since this is the case, the relative stabilities of isomers 9 and 10 can be compared by just looking at one conformational form; the chair isomers 9 and 10 have a difference in energy of ~4.6 kcal mol-1, favouring 10 as the more stable one. Looking at the contributions to the absolute energies, the Bend energies of both differ the most; 15.8801 kcal mol-1 for chair isomer 9 and 10.6662 kcal mol-1 for chair isomer 10, thus giving a difference of ~5.2kcal mol-1. This excess difference is negated by other energy terms to account for the difference in absolute energies, but it can be said that the Bend energy difference is the major contributor to the difference in absolute energies.
During subsequent functionalisation of the alkene, it reacted significantly slower than usual. This is beacause these alkenes are hyperstable. This is proven by measurements of Olefinic Strain (OS), which compares the difference in total strain energy of the most stable conformer of the parent hydrocarbon, and that of the olefin in its most stable conformation, by subtracting the former from the latter. These are usually positive in value for most alkenes, and specifically for those that follow Bredt's Rule (most bridgehead olefins). However, in this case, these hyperstable alkenes would be considered to be anti-Bredt molecules, as their OS values are negative, indicating that their parent hydrocarbons are less stable than the more stable olefins! This means that these hyperstable alkenes are particularly unreactive because of their positions at bridgeheads. This can be explained by the fact that at the bridgehead positions of middle rings incorporated in polycyclic systems, the bridgehead carbon favours an sp2 type configuration, and so an alkene at the bridgehead promotes this, meaning the structure wouldn't want to lose this favourable configuration by the alkene reacting. The high unreactivity can also be attributed to the almost 'cage' structure of the olefin.[6] Using the MMFF94 Force Field produces higher absolute energies of each conformer, therefore perhaps not accounting the OS energy and not as good a force field to use to optimize/minimize the geometries/energies.
Modelling using Semi-Empirical Molecular Orbital Theory
Regioselective Addition of Dichlorocarbene
Part 1
(Using MOPAC/PM6 alongside MM2 for this section)
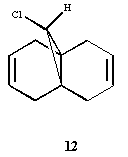
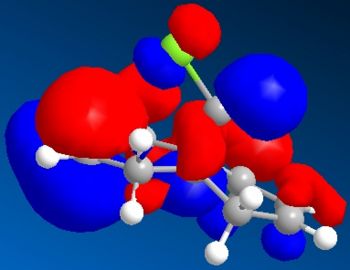
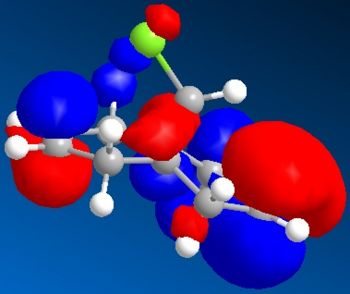
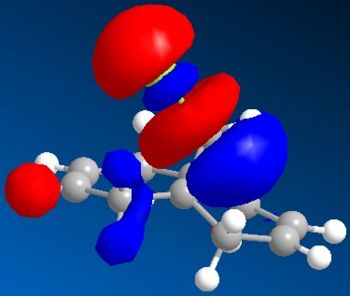
Electronic/molecular orbital interactions play a key part in reactivity of compounds, alongside the thermodynamics recently evaluated in the previous sections using MM2. Here MOPAC/PM6 MO methods will be used to account for these interactions, in studying the reactivity of compound 12 with electrophilic reagents such as dichlorocarbene or peracid. MOPAC/PM6 allows the molecular orbital energies to be calculated and displayed graphically. The above Jmol is the MM2/MOPAC-PM6 optimised geometry of compound 12. Below are the energies after MM2 and MOPAC/PM6 optimisation, and the key frontier molecular orbitals needed to study compound 12:
| MM2 Optimisation | MOPAC/PM6 Optimisation |
| 17.8971 | 19.74030 |
 |
 |
 |
 |
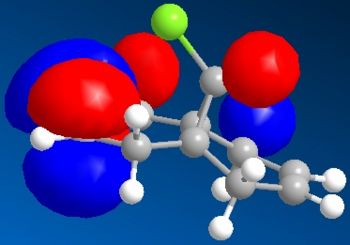 |
As can be seen above, the HOMO shows that there is a much larger electron density on the π-face of the alkene nearest, or endo to the Cl atom, which indicates it is a lot more nucleophilic, compared to the exo alkene, and so regioselective attack by the electrophilic reagent is more likely to occur at the endo alkene. The higher reactivity of the endo alkene can be attributed to the relative stability of the exo alkene, which is due to a stabilising antiperiplanar interaction between the Cl-C σ* orbital (LUMO+1) and the occupied exo-π orbital (HOMO-1), stabilising this π-MO and making this alkene more stable and less reactive. The HOMO-1 MO is also relatively diffuse compared to the HOMO, and as the HOMO-1 displays a majority electron density on the exo alkene (therefore signifying dominant interactions with this alkene in this MO), in effect it shows that this alkene is less nucleophilic. Proof of the π-σ* negative hyperconjugation can be found in the resulting geometrical distortion of the bicyclic structure:
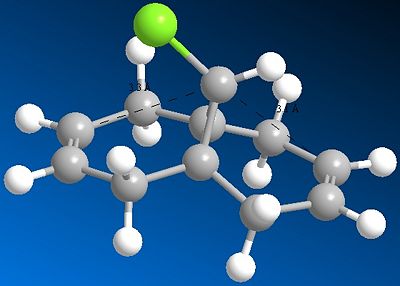
Here the distance to (either) exo alkene carbon and the central bridgehead carbon is 3.1Å, compared to 3.3Å for either endo alkene carbon; the stabilising negative hyperconjugation interaction distorts the alkene towards the C-Cl bond and shortens the distance thus. The difference between the two distances (0.2Å) is in moderate accordance with the literature value.[7]
Part 2
(Using MOPAC/PM6 and DFT-type Gaussian B3LYP/6-31 G(d,p) geometry optimization and frequency calculation alongside MM2 for this section)
The MO methods used to account for electronic interactions in analysing the thermodynamics and reactivity of compounds can also provide analytical data, e.g. spectroscopic data. The vibrational frequencies (IR spectral peaks) can be obtained in this way. Here a quantum mechanical approach is taken, by using DFT-type Gaussian B3LYP/6-31G(d,p) sent to the SCAN supercomputer, to optimise the structures and then find the vibrational frequencies. (Pre-optimisation was undertaken for both molecules using MM2 and then MOPAC/PM6, so as to prepare them for Gaussian optimisation, which takes longer to run the calculation otherwise!) This was done for Compound 12 DOI:10042/to-6480 , and 13 DOI:10042/to-6481 , which is a hydrogenated version of 12 where the exo double bond only is replaced by a single C-C bond:
 |
 |
The following predicted IR spectra were obtained:
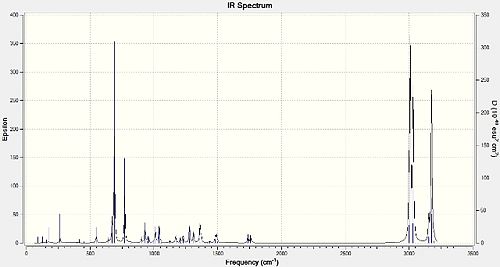 |
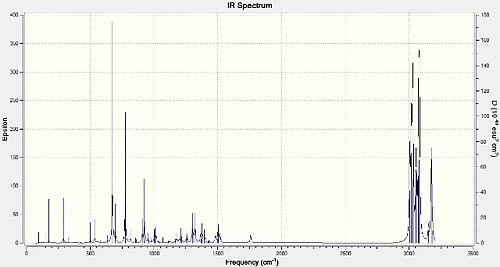 |
Looking in particular at how the Cl-C bond affects the key vibrational frequencies of the molecules, the Cl-C and the C=C (two for the diene 12 and one for the monoalkene 13) stretches were recorded:
| Compound 12 | Compound 13 | |
|---|---|---|
| Cl-C stretch | 770.89 | 774.95 |
| Exo C=C stretch | 1737.05 | N/A |
| Endo C=C stretch | 1757.35 | 1758.06 |
The Cl-C stretches observed and recorded were those that in particular had a very high IR intensity, whereas the C=C stretches were quite weak in intensity. This due to the dependence of IR peak intensities on the selection rule that IR absorption and subsequent vibration must be accompanied by a change in dipole moment. While the C=C bond is relatively non-polar and so any vibration won't lead to a large change in dipole moment, the Cl-C bond is very polar, and so vibrations do lead to a large change in dipole moment. This means the IR absorptions for Cl-C will be 'allowed', giving them a large IR intensity, whereas those for the C=C bonds are 'disallowed', giving them weak IR peak intensities. Comparing them for 12 and 13, it can be seen that the Cl-C stretches differ the most, with 12's stretch being lower in value by 4.06cm-1, whereas the difference between the endo C=C stretches is only 0.71cm-1 (smaller for 12). The exo C=C stretch for 12 is lower in value than its endo C=C stretch by 20.3cm-1. The C=C stretches are higher in energy than the Cl-C stretches (by about 1000cm-1 because the C=C have a much higher bond electron density and hence bond energy and therefore higher vibrational frequencies/energies in order to make them vibrate/stretch. Although 12 and 13's stretches do differ, this isn't significant enough to be explained in terms of relevant stereoelectronic/orbital effects. However, the difference in the endo/exo C=C stretches for 12 can be explained by the fact that the exo C=C bond has less electron density compared to the endo C=C bond, due to the negative hyperconjugation interaction (π-σ*) previously discussed. Therefore, the exo C=C bond is a 'weaker' double bond and requires less energy to vibrate, culminating in a lower vibration frequency.
Modelling using DFT-based Molecular Orbital Methods: MiniProject-A Key Intermediate in the Total Synthesis of (+)-Furanomycin[8]
(+)-Furanomycin is an antibiotic α-amino acid, that contains a 2,5-dihydrofuran moeity. During its total synthesis, several key intermediates are produced. One of these intermediates is diastereomeric; the diastereoisomeric adducts 22a and 22b below:
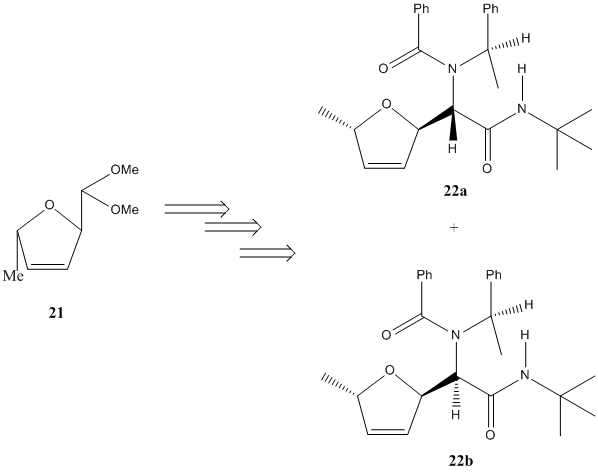
These stereoisomers are produced in a 1:1 yield ratio, indicating no stereoselective preference of reagent attack, and so neither product is preferred. To confirm that MO methods can be used to predict analytical (spectroscopic) data, the 13C NMR spectra of these stereoisomers, and their Optical Rotations, will be calculated using the DFT-type MO method Gaussian MPW1PW91/6-31G(d,p) for the 13C NMR (GIAO method), and DFT cam-B3LYP/6-311G(d,p) for the OR (cam-B3LYP is a Cambridge variant of B3LYP). The data will then be compared to the literature values to check its accuracy of prediction, and specifically for 13C NMR the assignments of NMR peaks to C atoms will be calculated and reported. (N.B. Initial optimisation of geometries of 22a and 22b is perfomed using ChemBio 3D MM2 Force Field, and then submitted to SCAN for DFT MPW1PW91/6-31G(d,p) for higher geometry optimisation.)
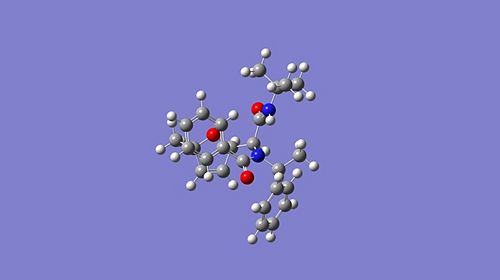
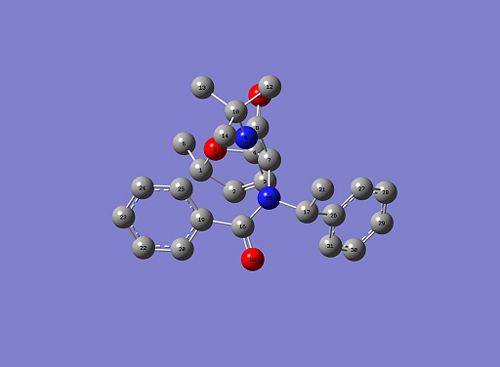
Here are the optimised geometries of both stereoisomers:

|
|
and here are the 13C NMR data for both isomers:
 |
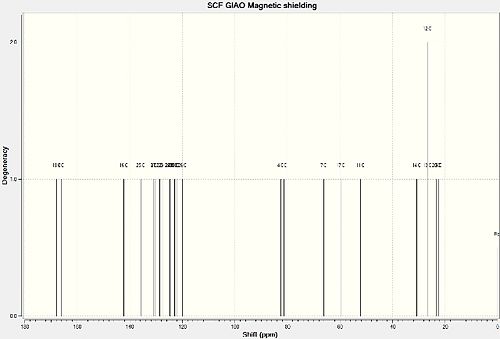 |
| Carbon Assignment | Predicted Chemical Shift | Literature Chemical Shift | Difference in Chemical Shifts |
|---|---|---|---|
| 18 | 173.3 | 173.7 | 0.4 |
| 8 | 171.7 | 170.0 | 1.7 |
| 16 | 142.3 | 138.9 | 3.4 |
| 25 | 135.8 | 137.3 | 1.5 |
| 3 | 130.9 | 133.0 | 2.1 |
| 27 | 130.3 | 130.0 | 0.3 |
| 2 | 128.7 | 129.5 | 0.8 |
| 29 | 127.3 | 128.8 | 1.5 |
| 28 | 124.9 | 128.1 | 3.2 |
| 24 | 124.8 | 128.1 | 3.3 |
| 22 | 124.7 | 128.1 | 3.4 |
| 21 | 123.3 | 127.6 | 4.3 |
| 30 | 123.0 | 127.6 | 4.6 |
| 31 | 122.8 | 127.6 | 4.8 |
| 23 | 122.2 | 127.2 | 5.0 |
| 26 | 119.9 | 126.0 | 6.1 |
| 4 | 82.5 | 82.3 | 0.2 |
| 1 | 81.4 | 81.0 | 0.4 |
| 7 | 66.3 | 68.1 | 1.8 |
| 17 | 59.8 | 59.0 | 0.8 |
| 11 | 52.3 | 51.0 | 1.3 |
| 14 | 30.8 | 28.7 | 2.1 |
| 12 & 13 | 26.7 | 28.7 | 2.0 |
| 20 | 23.3 | 21.3 | 2.0 |
| 6 | 22.4 | 17.9 | 4.5 |
 |
 |
| Carbon Assignment | Predicted Chemical Shift | Literature Chemical Shift | Difference in Chemical Shifts |
|---|---|---|---|
| 16 | 173.9 | 172.1 | 1.8 |
| 8 | 170.0 | 167.3 | 2.7 |
| 26 | 138.3 | 139.1 | 0.8 |
| 2 | 133.3 | 137.3 | 4.0 |
| 19 | 131.8 | 132.6 | 0.8 |
| 20 | 131.2 | 132.6 | 1.4 |
| 31 | 128.9 | 130.0 | 1.1 |
| 25 | 128.4 | 129.5 | 1.1 |
| 23 | 128.1 | 129.5 | 1.4 |
| 30 | 125.7 | 128.8 | 3.1 |
| 3 | 125.2 | 128.6 | 3.4 |
| 29 | 125.0 | 128.0 | 3.0 |
| 28 | 124.7 | 128.0 | 3.3 |
| 22 | 123.6 | 126.1 | 2.5 |
| 27 | 123.2 | 126.1 | 2.9 |
| 24 | 122.3 | 126.1 | 3.8 |
| 4 | 85.8 | 85.4 | 0.4 |
| 1 | 80.1 | 81.9 | 1.8 |
| 7 | 65.5 | 63.5 | 2.0 |
| 17 | 54.5 | 57.6 | 3.1 |
| 10 | 52.3 | 50.6 | 2.3 |
| 14 | 30.8 | 28.6 | 2.2 |
| 13 | 27.1 | 28.6 | 1.5 |
| 12 | 26.5 | 28.6 | 2.1 |
| 6 | 21.8 | 21.6 | 0.2 |
| 21 | 19.2 | 18.4 | 0.8 |
(N.B. Carbons belonging to amide carbonyls were corrected due to systematic error in the following way: δcorr = 0.96δcalc +12.2. These carbons were C-8 and C-18 for 22a and C-8 and C-16 for 22b.) Looking at the data above there a few observations. Firstly, looking at the differences between the predicted and literature values, the agreement is fairly good for both 22a and 22b, more so for 22b as 22a has C-23 and C-26 with differences of 5.0 and 6.1 respectively (possibly suggesting an incorrect conformation was used here), but beyond these two carbons the agreement is good; this supports the usage of 13C NMR GIAO method in predicting the 13C NMR spectra of molecules. Also, the literature values were not assigned, and as they gave less values then there were carbons in both intermediates, some prediction was made into which chemical shifts provided by the literature fitted the assigned carbons; this is why the same literature value can be seen for different carbons. Finally, a general trend in differences seen is that for those carbons at larger chemical shift value (i.e. very downfield), the literature value is larger than the predicted, but for those that are upfield, the reverse is true. This in effect seems to 'squash' the range of the predicted 13C NMR spectral peaks relative to those for the literature.
The Optical Rotations were also calculated for both intermediates:
| Intermediate 22a DOI:10042/to-6492 | Intermediate 22b DOI:10042/to-6493 | |
|---|---|---|
| Predicted | +48.52 | +357.64 |
| Literature | +253 | +82 |
As can be seen from this, there is no recognisable agreement between the literature and predicted set of values. This shows that the prediction of optical rotation has its limits when using a DFT-type MO method, as the technique is very sensitive to conformation and size (number of non-hydrogen atoms in particular), and so as both intermediates are fairly large and could have conformational changes to their structures, the technique has failed thus.
One technique that could help in differentiating spectroscopically is NOESY, which is a 2-dimensional NMR technique that can account for the spatial arrangement of atoms, or in the case of 22a and 22b, the specific proton which is found in spatially different positions relative to the other groups around (wedged/dashed proton). It does this by accounting for the coupling of protons that differs due to spatial arrangement.
References
- ↑ K. Alder and G. Stein, Liebigs Ann. Chem., 1933, 504, 210-257.DOI:10.1002/jlac.19335040115
- ↑ A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry., 1986, 51, 838.DOI:10.1021/jo.00356a016
- ↑ S. Leleu, C.; Papamicael, F. Marsais, G. Dupas, V.; Levacher, Vincent, Tetrahedron: Asymmetry, 2004, 15, 3919-3928.DOI:10.1016/j.tetasy.2004.11.004
- ↑ D. L. Boger et al., J. Am. Chem. Soc., 1999, 121, 3226.DOI:10.1021/ja990189i
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 32, 319-322.DOI:10.1016/j.tetasy.2004.11.004
- ↑ W. F. Maier and P. V. R. Schleyer, J. Am. Chem. Soc., 1981, 103, 1891-1900.DOI:10.1021/ja00398a003
- ↑ B. Halton, R. Boese and H. S. Rzepa, J. Chem. Soc., 1992, Perkin Trans. 2, 447-448.DOI:10.1039/P29920000447
- ↑ J. E. Semple, P.C. Wang, Z. Lysenko, and M. M. Joullié, J. Am. Chem. Soc., 1980, 102 (25), 7505-7510.DOI:10.1021/ja00545a018
