Rep:Mod:ftino06

The Cope Rearrangement - Rectants and Products

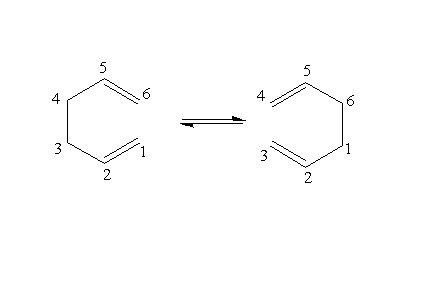
The Cope rearrangement of 1,5-hexadiene was studied to locate the low-energy minima and transition structures on the potential energy surface and to determine the preferred reaction mechanism . The reaction is considered to occur in concerted mechanism via a chair or a boat transition structure, the boat transition structure being higher in energy.

A molecule of the 1,5-hexadiene with an anti linkage (anti peri planar for the four central carbons) (anti1) was drawn in Gaussview and the structure cleaned up . The structure was then optimized in Gaussian using the HF/3-21G method. The %mem was set to 250MB under the Link 0 tab. The energy of the optimised structure is -231.68907hartree. The final structure has a symmetry point group of C_2h.the anti 1 conformer drawn is the anti3 conformer in the table. It has the same energy and point group as that given in the table. A molecule of the 1,5-hexadiene with a gauche linkage(gauche1) was drawn in Gaussview and the structure of the molecule was cleaned up . The structure was optimized in Gaussian using the HF/3-21G method. The energy of the gauche conformer is -231.69153hartree and its point group is C₂.The gauche conformer drawn is the gauche 4 conformer in the table and has the same energy and symmetry point group.

It is expected that the lowest energy conformation will be that with an anti linkage (anti2 – anti2 conformer in table in appendix 1). This is because the R groups (with reference to the middle C-C) will be anti peri planar to each other therefore steric interactions will be minimal. This molecule of 1,5-hexadiene with an anti linkage (anti2) was drawn in Gaussview and the molecule was cleaned up . The structure was then optimized using Gaussian and the HF/3-21G method . The structure was found to have an energy of -231.69254hartree and point group C_i. However by comparing to all the other 1.5-hexadiene conformations, it is found not to be the lowest in energy. The lowest energy conformation has a gauche linkage (gauche2 – (gauche 3 conformer in table in appendix 1)). This structure has an energy of -231.69266hartree and a point group of C₁. The reason for the stability of the gauche conformer can be seen in its HOMO (bottom left), where there is overlap between the pi bonding orbitals of the two alkenes. This orbital interaction is not seen in the HOMO of the anti conformer(top left). The LUMO of the anti conformer (top right) shows the two pi antibonding orbitals and a nodal plane going though the middle C-C, whereas in the gauche conformer (bottom right)there is orbital overlap between the pi antibonding orbitals of the two alkenes. This secondary orbital overlap has a significance in stabilising the gauche conformer compared to the anti conformer.

The C_i anti2 conformer was optimised at the Hartree Fock / 3-21G level. The energy of the molecule is -231.69254hartree and has point group C_i. The C_i anti conformer given in the table (appendix 1) has an energy of -231.69254 hartree. The C_i anti2 conformation was reoptimized at the B3LYP/6-31G* level using the DFT method. The energy of the molecule decreased to -234.61171683 hartree, the point group stays the same, C_i.

**C_i anti geometry**
Bond angle	HF/3-21G	DFT/6-31G*
C11-C9-C1/ C14-C7-C4	124.8	125.3
C7-C4-C1/C4-C1-C9	111.4	112.7
H2-C1-H3	107.7	106.7
C7-C4-C1-C9	180.0	180.0
C11-C9-C1-C4/ C14-C7-C4-C1	114.7	118.6

The DFT B3LYP/6-31G* is a higher optimisation level, this can be seen by the further stabilisation of the molecule (decrease in energy). The point group of the molecule does not change but some of the bond angles change. Significant changes in bond angles can be seen in the C-C-C-C dihedral angle which gets larger by about 4⁰. The R groups are anti peri planar about the middle C-C bond. The increase in the other angles stabilises the molecule by increasing the separation between the groups and thus reducing steric interactions.

Using the optimized B3LYP/6-31G* structure, a frequency calculation was run using the same basis set and method. The vibrations were viewed and they all had positive frequencies, which shows that the structure is at an energy minimum. The vibration with frequency at 940 cm^-1 is the symmetric bending (wagging)of the alkene terminal hydgrogens (-C=CH₂). The C=C antisymmeric stretch has frequency 1734 cm^-1, the C=C symmetric stretch is at 1731 cm^-1 but has an intensity of zero as there is a zero change in dipole moment. The alkyl (central CH₂CH₂) symmetric C-H stretches have frequency 3031 cm^-1 and the antisymmetric stretches have frequency 3080 cm^-1. The alkene terminal C-H symmetric stretch has frequency 3155 cm^-1 and the antisymmetric stretch has frequency 3233 cm^-1. The alkene C-H (H₂C=CH-) antisymmetric stretch as frequency 3137 cm^-1. The following table shows a summary of the energies of the anti C_i sturcture.

**Summary of energies (in hartree) for reactant (anti2)**
Method	Electronic energy	Sum of electronic and zero point energies	Sum of electronic and thermal energies	Sum of electronic and thermal enthalpies	Sum of electronic and thermal free energies
HF/3-21G	-231.692535	-231.539542	-231.532571	-231.531627	-231.570899
DFT/6-31G*	-234.611717	-234.469185	-234.461847	-234.460903	-234.500732

• Sum of electronic and zero point energies: potential energy at 0K including the zero point vibrational energy (E= E_elec + ZPE) • Sum of electronic and thermal energies: the energy at 298.15K and 1atm of pressure which includes contributions from the translational, rotational and vibrational energy modes at this temperature (E =E + E_vib + E_rot + E_trans) • Sum of electronic and thermal enthalpies: contains an additional correlation for RT (H=E+RT) • Sum of electronic and thermal free energies: includes the entropic contribution to the free energy (G=H-TS)

The Cope Rearrangement - Chair and Boat Transition Structures

The allyl fragment (CH₂CHCH₂) was drawn in Gaussview and optimised using the HF/3-21G level. The optimized allyl structure was copied and pasted twice and the two ally structures were orientated to look like the chair transition structure. The distance between the terminal ends of the allyl fragments was approximated to 2.2Å. The chair transition structure was optimised using two different ways.

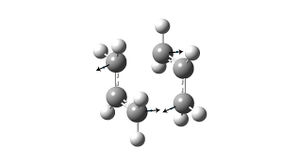
Firstly, the chair transition structure was optimised to a Berny transition state using the Hartree Fock method and the 3-21G basis set. The frequency was calculated simultaneously. The distance between the terminal carbons of the ally fragments changed to 2.02Å. All the frequencies were positive apart from the first one which is negative (imaginary frequency), this shows that it is a transition state. The imaginary frequency has a magnitude of -818 cm^-1. This vibration corresponds to the Cope rearrangement. Two terminal carbons of the allyl fragments move towards each other and the other terminal carbons move away from each other.

Secondly, the chair transition structure was optimised using the frozen coordinate method. The distances between the terminal carbons of the allyl fragments were frozen to 2.2Å via the redundant coordinate editor. The structure was optimised as a minimum using the HF/3-21G method. The optimised structure looked like the one obtained using the previous method, but the bond breaking/forming distances were fixed to 2.2Å. The structure was re-optimised as a transition state with the bonds unfrozen and force constants were not calculated as in the first method. The bond breaking/forming distances changed to 2.02Å in the optimised structure, this is the same result that was obtained using the first method of optimisation.

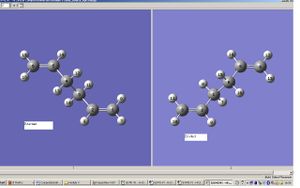
The boat transition structure was optimised using the QST2 method. In this method, the products and reactants are specified and the calculation interpolates to find the transition structure between them. The numbering on the product molecule was changed so that it would correspond to the numbering if the reactant molecule had rearranged, as seen in the picture on the left. The structures were optimised, but failed to give a boat transition structure, instead it gave a chair transition structure. This is because when the calculation interpolated between the two structures, it simply translated the top allyl fragment and did not consider rotating it. To make up for this, the reactant and product structures were modified by making the central C2-C3-C4-C5 dihedral angle 0⁰ and the inside C-C-C angles were reduced to 100⁰ (see picture on right above). The modified structures were optimised as a transition state using the QST2 method as before, a boat transition structure was obtained.

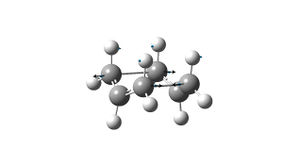
The structure has one imaginary vibrational frequency at -840 cm^-1, which shows the bond breaking/forming motion of the Cope rearrangement (see displacement vectors in picture on the left). The distance between the previosly terminal carbons, shortens as they form a bond, and the previously double bonds legthen to singl bonds. The distance between the terminal carbons of the allyl fragments in the boat transition strucure is 2.14Å. this distance is longer than that observed in the chair TS (2.02Å)

The Intrinsic Reaction Coordinate (IRC) method in Gaussian allows us to follow the minimum energy path from a transition structure to the local minimum on a potential energy path . It creates a series of points (50 points were specified initially) by taking small geometric steps in the direction where the gradient of the energy surface is steepest. The IRC method was run on the optimised chair transition structure. The reaction coordinate was calculated in the forward direction, thus the reaction pathway leading from the transition structure to the product structure. The finished calculation showed that a minimum geometry had not been reached as it had gone through all 50 points and had an imaginary frequency of -817cm^-1. The last structure in the IRC calculation had an energy of -231.68064hartree. The C-C distance between the terminal bonding carbons of the allyl fragments was 1.571Å. The dihedral angle about the middle C-C-C –C was 58.8⁰.

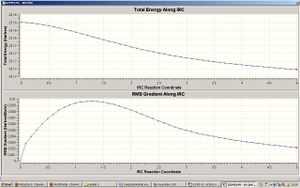
As can be seen from the IRC graphs, the total energy of the structure decreases as you go along the IRC reaction coordinate and the gradient is steepest as we move away from the transition structure and gradually becomes flatter close to the minimum geometry. To try to get to a minimum energy geometry, 3 options were used :

1) The last structure on the IRC was optimised to a minimum using the HF/3-21G method. The energy of the minimum is -231.69167hartree and the C-C bond distance is 1.55Å. The dihedral angle about the central C-C-C-C is 64.2⁰. The structure has a point group of C₂.

2) The IRC was restarted and the number of points until it reaches a minimum were reset to 100 DOI:10042/to-4233 . The final calculation showed that a minimum still had not been reached after 100 points, as the structure has an imaginary frequency of -816cm^-1. The last structure in this calculation had an energy of -231.6905hartree, the C-C bond distance between allyl fragments is 1.56Å, the central C-C-C-C dihedral is 73.3⁰.

3) The IRC was restarted, the number of points was set to 50 and force constants were computed after every step. The final calculation ended at point 47 and the last structure had no imaginary frequencies, which shows that an energy minimum had been reached. The structure has an energy of -231.69166hartree. The energy is the same as that obtained using the minimising option (1). The C-C-C-C dihedral angle is 64.6⁰ and the newly formed bond is 1.55Å. The structure has C₂ point group. DOI:10042/to-4234 The final minimum energy structure (product) obtained is that with a gauche linkage and C₂ point group, this is not the most stable 1-5-hexadiene conformer.

The boat and chair transition structures were re-optimised at the B3LYP/6-31G* level and their frequencies were calculated. the differences in energy are shown below:

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.314072	-231.466697	-231.461338	-234.272877	-234.414930	-234.409009
Boat TS	-231.299045	-231.450924	-231.445294	-234.264004	-234.404525	-234.398164
*Reactant (anti2)*	-231.532571	-231.539542	-231.532571	-234.461847	-234.469185	-234.461847

*1 hartree = 627.509 kcal/mol

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.71	44.70	34.05	33.15	33.5 ± 0.5
ΔE (Boat)	55.61	54.77	40.57	39.96	44.7 ± 2.0

A summary of the differences in geometry between the reactant (anti2) and the chair and boat transition structures are shown below:

Summary of goemetry changes (angles in degrees)

	HF/3-21G		B3LYP/6-31G*
	C-C-C allyl fragment	C-C-C-C central carbons dihedral	C-C-C allyl fragments	C-C-C-C central carbons dihedral
Chair TS	120	55	120	54
Boat TS	122	0	122	0
*Reactant (anti2)*	125	180	125	180

Summary of goemetry changes (bond lengths in angstorms)

	HF/3-21G		B3LYP/6-31G*
	C-C bond between allyl fragments	C-C bonds within allyl fragment	C-C bond between allyl fragments	C-C bonds within allyl fragment
Chair TS	2.02	1.39	1.97	1.39
Boat TS	2.14	1.38	2.20	1.39
*Reactant (anti2)*	1.55	1.51, 1.32	1.55	1.50, 1.33

The boat and chair transition structures were re-optimised at the B3LYP/6-31G* level and their frequencies were calculated. The energies of the reactant and transition structures are lower using the B3LYP/6-31G* method compared to the HF method, due to the DFT method being a higher level calculation method. Looking at the HF method, it can be seen that the reactant is lower in energy than the transition states and the chair transition state is approximately 9.43kcal/mol lower in energy than the boat transition state. The same trend is seen in the DFT method but the difference in energy between the transition structures is 6.81kcal/mol. The DFT calculated activation energies are more comparable to the experimental values than the HF values. The boat transition state has higher activation energy than the chair transition state. In the reactant the ally fragments are antiperiplanar (looking down the middle C-C bond), in the chair transition state they are gauche and in the boat transition state they are eclipsed (synperiplanar), which shows why the boat TS is high in energy due to high steric interactions. The bond lengths of the transition states and reactant are similar apart from the C-C bond between the allyl fragments, which is longer in the TS as it is a partly formed sigma bond and in the reactant, the single and double bonds are localised compared to the delocalisation in the transition states.

The Diels Alder Cycloaddtion - Cis-Butadiene with Ethene

The Diels Alder reaction is classed as a pericyclic reaction. The pi orbitals of the dieneophile form new sigma bonds with the pi orbitals of the dine. Usually the diene is electron rich and its HOMO interacts with the LUMO of the dieneophile and the HOMO of the dieneophile interacts with the LUMO of the diene. The cycloaddtion of butadiene with ethylene was studied.

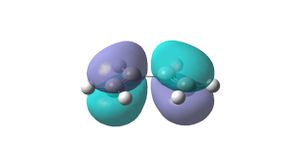
The structure of cis- butadiene was drawn in Gaussview and optimised using the AM1 semi-empirical molecular orbital method. The energy of the optimised structure is 0.04880142hartree. Its point group is C_2v. The HOMO is antisymmetric with respect to the plane of symmetry (top right picture) and the LUMO is symmetric with respect to the plane (bottom right picture).

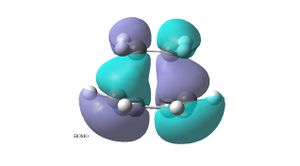
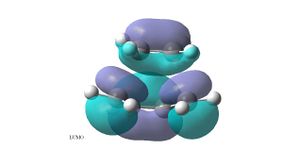
The ethylene plus cis butadiene transition structure was optimised as a Berny TS using the semi-empirical AM1 method. The HOMO of the transition structure is antisymmetric wrt to the plane of symmetry and shows that the HOMO of the cis- butadiene interacts with the LUMO of the ethylene. The LUMO of the transition structure is symmetric wrt the plane and shows the HOMO of the ethylene and the LUMO of the butadiene, but there is a nodal plane between the two, they do not interact as it is an antibonding orbital. The reaction is allowed because the HOMO of the butadiene interacts with the LUMO of the ethene, both of these orbitals have the same symmetry (atnisymmetric) about the plane. Significant orbital overlap can be seen in the HOMO of the transition structure.

The transition structure has point group C_s. A typical sp³ C-C bond length is 1.54Å and a typical sp² C-C bond length is 1.34Å DOI:10.1023/B:RUGC.0000025528.22795.be , and a carbon atom has a Van der Waals radius of 1.7Å. The partly formed sigma C-C bond length is 2.18Å. The C-C bond length of the partly formed sigma bond shows that a sigma bond has not formed in the TS as the C-C distance is longer than that of a sp³ C-C bond, but the atoms are not completely isolated either as the distance between them is shorter than both their Van der Waals radii combined (3.4Å). This shows that there is a sharing of electron density between the atoms, thus the partial formation of a bond. All the other bonds are between 1.38-1.40Å, which means that they are partial double bonds as they are shorter than single bonds, the pi electron density is delocalised over the bonds.

The optimised structure has an imaginary frequency of -956 cm^-1. The imaginary frequency shows the synchronous formation of the two bonds, the distance between the terminal carbons of the butadiene fragment and the carbons of the ethylene fragment shortens . The C-C bond of the ethylene fragment lengthens as it is going from a double bond to a single bond. The C-C double bonds of the butadiene fragment lengthen and the C-C single bond shortens as it becomes a double bond. The lowest positive frequency (147 cm^-1) is a rocking motion of the two fragments in opposite directions, with the ethylene fragment being displaced more that the butadiene fragment. The displacement vectors can be seen in the picture of on the bottom left.

An IRC was run on the cyclohexene transition structure using the AM1 semi-empirical method. The number of points was specified to 50, but the calculation stopped at the 27th point. The energy of the structure decreased to -0.01099613hartree. DOI:10042/to-4237 the final structure obtained represented that of the final product. The newly formed sigma bonds were 1.52Å long. The double bond was 1.34Å, two of the single bonds (previously double bonds in butadiene) were 1.48Å and the last single bond (previously ethene) was 1.52Å.

The Diels Alder Cycloaddition - Cyclohexa-1,3-diene with Maleic Anhydride

Cyclohexa-1,3-diene react with maleic anhydride to give the endo product. the reaction is kinetically controlled, which means that it goes via the lowest energy trasntion state. The exo product is the thermodynamically more stable product, but has transtion state which is higher in energy than the endo one.

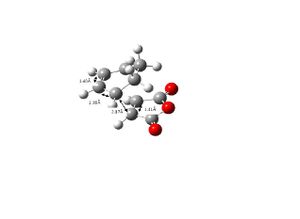
The endo and exo were optimised using the AM1 semi-empirical method. The energy of the endo transition structure is -0.05159430 hartree and that of the exo structure is -0.05050326 hartree. The exo transition structure is higher in energy than the endo transition structure. The bond lengths in the endo and exo transition structures are the same as can be seen from the pictures above. For the exo structure the C-C through space distance between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the opposite –CH₂CH₂- is 2.94Å. For the endo structure the C-C through space distance between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the opposite –CH=CH- is 2.89Å.

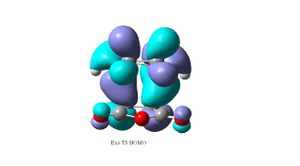
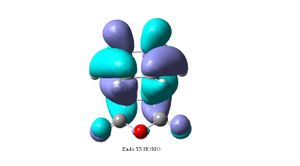
The exo form could be more strained due to sterics between the carbonly groups of the maleic anhydride fragment and the opposite -CH₂CH₂- fragment. By looking at the HOMO of the endo (top right) transition structure, there is a nodal plane between the -(C=O)-O-(C=O)- fragment and the rest of the MO system (which is the HOMO of the diene interacting with the LUMO of the maleic anhydride alkene). In the HOMO of the exo (top left) the -(C=O)-O-(C=O)- fragment has the same phase as the rest of the system. The orbitals on the -(C=O)-O-(C=O)- fragment are located on the exo Oxygen atoms (O lone pairs) and are in-phase with the opposite -CH₂CH₂- fragment. This suggests that there could be a possible stabilising orbital interaction between the two, the large distance between the two fragments (2.94Å) means that the interaction will be weak. This suggests that the exo transition structure should be more stabilised than the endo structure due to the secondary orbital overlap effect. However the exo is found to be less stable than the endo, which shows sterics play a bigger role in the destabilisation of the exo transition structure. The secondary orbital overlap effect is a weak favourable/stabilising interaction, however in the case of the exo TS, it is overridden by the steric interactions. By looking at the HOMO-1 of the endo TS (bottom right), there is a possible secondary orbital overlap between the -(C=O)-O-(C=O)- fragment and the pi bonding orbital of the –HC=CH- fragment, this is not seen in the HOMO-1 of the exo TS(bottom left). This could be the stabilising effect in the endo compared to the exo.

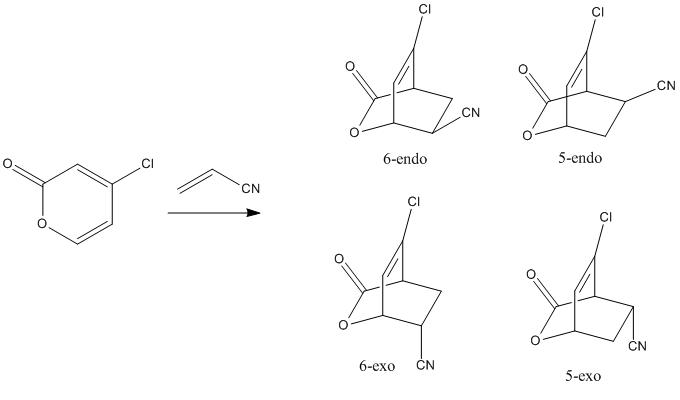
Mini Project -Computational investigation of Diels Alder cycloaddtion of 4-chloro-2(H)-pyran-2-one with acrylonitrile

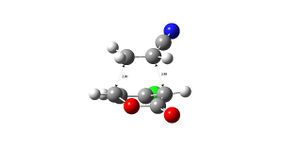
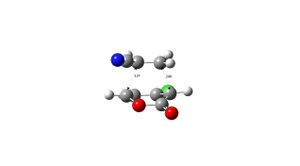
To understand and predict the regio- and stereoselectivity of the pyrone cycloaddtions calculations were carried out on the four transition states leading to the four possible stereoisomers in the cycloadditions of 4-chloro-2(H)-pyran-2-one with acrylonitrile and methyl acrylate. DOI:10.1021/jo0348827 I am going to investigate the reaction transition states of the cycloadditon between 4-chloro-2(H)-pyran-2-one with acrylonitrile. Acrylonitrile is an electron deficient dienophile.

**Optimised structures of Endo/Exo transition states (bond lengths in angstroms)**
5 exo	5 endo

6 exo	6 endo

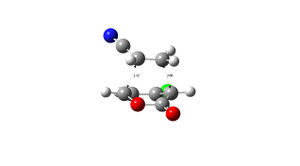**Energies of Endo/Exo transition states (in hartree)**
5 exo	5 endo	6 exo	6 endo
-973.750259	-973.752825	-973.752368	-973.755160

The structures of the stereoisomers were optimised using Gaussian, initially at the semi-empirical AM1 level then re-optimised using B3LYP/6-31G*.The 6endo transition structure was found to be the lowest in energy and is likely to be the most abundant in a reaction mixture and the 5exo has the highest energy. the results obtained match those given in the literature DOI:10.1021/jo0348827 .