Rep:Mod:fred345

The Hydrogenation of Cyclopentadiene Dimer

Isomers of the Cyclopentadiene Dimer

The total energy of the first isomer of the cyclopentadiene dimer is 55.374 kcalmol^-1 and the total energy of the second isomer of the cyclopentadiene dimer is 58.191 kcalmol^-1, this means that the first isomer (the exo dimer) is the thermodynamically favoured isomer because it is the most stable. Despite being less stable, The second isomer (the endo dimer) is the predominant isomer because it is the kinetically favoured isomer; for a Diels-Alder reaction, kinetic reaction control prevails at a temperature of 300 K. The plane to plane orientation of the two dimers, in the endo transition state, gives the correct symmetry for the HOMO and LUMO of the two dimers to interact (secondary orbital overlap effect); there is no such favourable interaction in the exo transition state.

(1)

(1)

Energy Term	Value (kcalmol-1)
Total van der Waals energy	12.805
Total Torsional Energy	-2.735
Total Angle Bending Energy	30.773
Total Bond Stretching Energy	3.543
Total Electrostatic Energy	13.014
Total Out-Of-Phase Bending Energy	0.0147
Total Stretch Bending Energy	-0.091

(2)

(2)

Energy Term	Value (kcalmol-1)
Total van der Waals energy	12.362
Total Torsional Energy	-2.952
Total Angle Bending Energy	33.186
Total Bond Stretching Energy	3.468
Total Electrostatic Energy	14.188
Total Out-Of-Phase Bending Energy	0.0219
Total Stretch Bending Energy	-2.083

The hydrogenated products

The difference in energy between the two hydrogenated products can be explained by examining the bond angle of the sp² hybridised carbons in each product. The C-C-C bond angles of the sp² carbons in dimers 3 and 4 are 107.1° and 112.9° (respectively); dimer 4 has a smaller deviation from the ideal sp² bond angle of 120° (less torsional strain).

(3)

This hydrogenated product has a total energy (using the MMFF94s force field) of 50.583 kcalmol^-1.

(3)

Energy Term	Value (kcalmol-1)
Total van der Waals energy	13.730
Total Torsional Energy	1.621
Total Angle Bending Energy	28.585
Total Bond Stretching Energy	3.379
Total Electrostatic Energy	5.113
Total Out-Of-Phase Bending Energy	0.016
Total Stretch Bending Energy	-1.860

(4)

This hydrogenated product has a total energy (using the MMFF94s force field) of 41.257 kcalmol^-1.

(4)

Energy Term	Value (kcalmol-1)
Total van der Waals energy	10.637
Total Torsional Energy	-0.378
Total Angle Bending Energy	24.686
Total Bond Stretching Energy	2.823
Total Electrostatic Energy	5.147
Total Out-Of-Phase Bending Energy	0.000
Total Stretch Bending Energy	-1.657

Atropisomerism in an Intermediate related to the Synthesis of Taxol

From the results below, it can be seen that isomer (9) is the most stable isomer. The reason why the two isomers react slowly is because they are less (ring) strained than their corresponding saturated hydrocarbon (due to the presence of the "bridge head"); alkenes that are less strained than their corresponding saturated hydrocarbon are called "hyperstable alkenes". In isomer 9, the bond angle of the sp² of the C-C-C bond is 123.5°, however, the same bond angle in intermediate 10 is 124°; isomer 10 is further away from the optimal bond angle of 120°. Isomer 9 is, hence, the most thermodynamically stable isomer.

(9)

There are two chair conformers and two boat conformers but only one of the chair conformers and one of the boat conformers were calculated.

Chair

(9)

Energy Term	Value (kcalmol-1)
Total van der Waals energy	33.121
Total Torsional Energy	0.342
Total Angle Bending Energy	28.251
Total Bond Stretching Energy	7.655
Total Electrostatic Energy	0.307
Total Out-Of-Phase Bending Energy	0.964
Total Stretch Bending Energy	-0.091

This conformer has a total energy of 70.550 kcalmol^-1.

Twist Boat

(9)

Energy Term	Value (kcalmol-1)
Total van der Waals energy	34.761
Total Torsional Energy	2.879
Total Angle Bending Energy	29.410
Total Bond Stretching Energy	7.947
Total Electrostatic Energy	0.319
Total Out-Of-Phase Bending Energy	0.940
Total Stretch Bending Energy	0.0687

This conformer has a total energy of 76.325 kcalmol^-1.

Summary

It can be seen that the twist-boat conformer is the lowest energy conformer; both conformers are an energy minimum.

(10)

There are two chair conformers and two boat conformers but only one of the chair conformers and one of the boat conformers was calculated.

Chair

(10 Chair)

Energy Term	Value (kcalmol-1)
Total van der Waals energy	35.763
Total Torsional Energy	7.508
Total Angle Bending Energy	21.317
Total Bond Stretching Energy	8.462
Total Electrostatic Energy	0.458
Total Out-Of-Phase Bending Energy	1.577
Total Stretch Bending Energy	-0.210

This conformer has a total energy of 74.875 kcalmol^-1.

Twist Boat

(10 boat)

Energy Term	Value (kcalmol-1)
Total van der Waals energy	38.786
Total Torsional Energy	8.533
Total Angle Bending Energy	23.833
Total Bond Stretching Energy	9.007
Total Electrostatic Energy	0.366
Total Out-Of-Phase Bending Energy	1.622
Total Stretch Bending Energy	-0.069

This conformer has a total energy of 82.077 kcalmol^-1.

Summary

Like for isomer 9, it can be seen that the twist-boat conformer is the lowest energy conformer; both conformers are an energy minimum.

Spectroscopy of an intermediate related to the synthesis of Taxol

Isomer 17

Chair

The isomer of another intermediate that is related to Taxol, isomer 17, was minimised using the MMFF94s mechanics force field; the total energy of the minimised structure is 104.901 kcalmol^-1.

17 chair

Energy Term	Value (kcalmol-1)
Total van der Waals energy	52.098
Total Torsional Energy	11.014
Total Angle Bending Energy	31.615
Total Bond Stretching Energy	15.900
Total Electrostatic Energy	-7.193
Total Out-Of-Phase Bending Energy	1.184
Total Stretch Bending Energy	0.283

Thermodynamics

Energy Term	Value (Hartree/particle)
Zero-point correction	0.468
Thermal Correction to Energy	0.490
Thermal Correction to Enthalpy	0.491
Thermal Correction to Gibbs Free Energy	0.422
Sum of electronic and zero-point energies	-1651.406
Sum of electronic and thermal energies	-1651.385
Sum of electronic and thermal enthalpies	-1651.384
Sum of electronic and thermal free energies	-1651.453

Twist Boat

17 boat

Energy Term	Value (kcalmol-1)
Total van der Waals energy	53.690
Total Torsional Energy	13.509
Total Angle Bending Energy	31.470
Total Bond Stretching Energy	15.969
Total Electrostatic Energy	-6.943
Total Out-Of-Phase Bending Energy	1.129
Total Stretch Bending Energy	0.397

the total energy of the minimised structure is 109.221 kcalmol^-1.

NMR Results for the Twist Boat Conformer

DOI:10042/26148

¹H NMR

A Gaussview image of the optimised isomer with all of the atoms numbered.

This is the predicted ¹³C NMR spectrum for the boat conformer of isomer 17, using tetramethylsilane (in chloroform) as a reference.

The NMR was generated using a B3LYP level of theory, with 6-31G(d,p) as the basis set. The experimentally generated NMR values for each of the protons are tabulated below:

δ (CHCl₃)

Proton	Chemical shift (ppm)
31-H	0.85
47-H	0.87
33-H	0.89
35-H	0.91
30-H	0.91
49-H	1.30
48-H	1.34
29-H	1.35
34-H	1.55
36-H	1.62
45-H	1.72
37-H	2.02
27-H	2.17
39-H	2.20
28-H	2.21
43-H	2.27
46-H	2.32
26-H	2.34
28-H	2.42
44-H	2.46
25-H	2.55
41-H	2.62
32-H	2.65
40-H	2.74
50-H	2.93
51-H	3.09
52-H	3.25
53-H	3.29
19-H	3.30
42-H	5.11

Literature values

1H NMR
δ (CDCl3, 300 MHz)
4.84 ppm	(dd,J=7.2,4.7Hz)	1 H
3.40-3.10 ppm	m	4 H
2.99 ppm	(dd,J=6.8,5.2 Hz)	1 H
2.80-1.35 ppm	(series of m)	14 H
1.38 ppm	s	3 H
1.25 ppm	s	3 H
1.00 ppm	s	3 H
1.00 - 0.80 ppm	m	1 H

42-H is a doublet of doublet; 19-H, 53-H, 52-H and 51-H are a multiplet; 50-H is a doublet of doublet; 40-H, 41-H, 25-H, 43-H, 28-H, 44-H, 26-H, 39-H, 46-H, 39-H, 37- H, 29-H and 45-H, 32-H, are a series of multiplets; 30, 31 and 32 are a singlet with an average chemical shift of 1.47 ppm; 47, 48 and 49 are a singlet with an average chemical shift of 1.17 ppm; 33, 34 and 35 are a singlet with an average chemical shift of 1.12 ppm; 29-H is a multiplet.

The NMR diagram that was generated computationally coincides reasonably well with the literature values that are tabulated above. It should be noted that the reason why the NMR shifts are different is because the solvent that was used for the computational results (chloroform) is not quite the same as the solvent that was used in the literature (deuterated chloroform). It should also be noted that the reason why the methyl protons aren't equivalent is because the Gaussian calculation, that was implemented onto the (twist boat conformer of) isomer 17, uses a static structure to model the isomer, rather than a dynamic one.

Based on the literature, proton 28 should be the most shielded proton but, due to the magnetic in-equivalence of the methyl protons, the average chemical shifts for the [30, 31, 32] and the [47, 48, 49] set of protons is lower.

¹³C NMR

This is the predicted ¹³C NMR spectrum for the boat conformer of isomer 17, using tetramethylsilane (in chloroform) as a reference.

δ (CHCl₃)

Carbon	Chemical shift (ppm)
5-C	19.73
10-C	22.38
6-C	26.31
17-C	26.50
4-C	28.27
18-C	32.30
20-C	34.13
14-C	36.27
22-C	41.85
23-C	45.49
11-C	47.35
2-C	47.67
7-C	51.91
3-C	53.41
9-C	54.56
13-C	61.31
12-C	88.91
15-C	124.98
16-C	145.52
8-C	217.00

Literature values

13C NMR
δ (C6D6, 75 MHz)
19.83 ppm
21.39 ppm
22.21 ppm
25.35 ppm
25.56 ppm
30.00 ppm
30.84 ppm
35.47 ppm
36.78 ppm
38.73 ppm
40.82 ppm
43.28 ppm
45.53 ppm
50.94 ppm
51.50
60.53 ppm
74.61 ppm
120.90 ppm
148.72 ppm
211.49 ppm

The literature ¹³C NMR matches very closely with the generated ¹³C NMR, despite the fact that the solvent that was used in the literature (deuterated benzene) is different from the solvent that was used to generate the ¹³C NMR (computationally); it can be seen that the chemical shifts that were generated are very similar to the corresponding chemical shifts that were quoted in the literature.

NMR Results for the Chair Conformer

DOI:10042/26194

¹H NMR

A Gaussview image of the optimised isomer with all of the atoms numbered.

This is the predicted ¹³C NMR spectrum for the chair conformer of isomer 17, using tetramethylsilane (in chloroform) as a reference.

The NMR was generated using a B3LYP level of theory, with 6-31G(d,p) as the basis set. The experimentally generated NMR values for each of the protons are tabulated below:

δ (CHCl₃)

Proton	Chemical shift (ppm)
47-H	0.59
31-H	0.82
35-H	0.88
30-H	0.92
33-H	0.92
49-H	1.16
29-H	1.49
34-H	1.57
37-H	1.60
45-H	1.63
48-H	1.75
36-H	1.90
38-H	1.95
27-H	2.11
28-H	2.13
46-H	2.27
43-H	2.28
40-H	2.36
39-H	2.38
26-H	2.41
25-H	2.44
32-H	2.64
41-H	2.70
44-H	2.73
51-H	3.00
50-H	3.03
19-H	3.16
52-H	3.22
53-H	3.31
42-H	5.15

42-H is a doublet of doublet; 19-H, 53-H, 52-H and 50-H are a multiplet; 51-H is a doublet of doublet; 40-H, 41-H, 25-H, 43-H, 28-H, 44-H, 26-H, 39-H, 46-H, 39-H, 37- H, 29-H and 45-H, 32-H, are a series of multiplets; 30, 31 and 32 are a singlet with an average chemical shift of 1.46 ppm; 47, 48 and 49 are a singlet with an average chemical shift of 1.17 ppm; 33, 34 and 35 are a singlet with an average chemical shift of 1.12 ppm; 29-H is a multiplet.

The NMR diagram that was generated computationally coincides reasonably well with the literature values that are tabulated above. It should be noted that the reason why the NMR shifts are different is because the solvent that was used for the computational results (chloroform) is not quite the same as the solvent that was used in the literature (deuterated chloroform).

Based on the literature, proton 28 should be the most shielded proton but, due to the magnetic in-equivalence of the methyl protons, the average chemical shifts for the [30, 31, 32] and the [47, 48, 49] set of protons is lower.

There's a very minimal difference between the generated NMR of the chair conformer and the generated ¹H NMR of the twist boat conformer.

¹³C NMR

This is the predicted ¹³C NMR spectrum for the chair conformer of isomer 17, using tetramethylsilane (in chloroform) as a reference.

δ (CHCl₃)

Carbon	Chemical shift (ppm)
5-C	19.73
10-C	22.90
6-C	26.40
17-C	26.40
29-C	29.32
18-C	31.01
14-C	35.33
22-C	40.57
11-C	42.17
23-C	45.95
2-C	46.69
7-C	51.55
3-C	52.48
9-C	57.04
13-C	60.64
12-C	90.65
15-C	124.68
16-C	145.13
8-C	145.52

The literature ¹³C NMR doesn't match very closely with the generated ¹³C NMR); only 19 peaks can be seen in the ¹³C NMR of the chair conformer, as opposed to 20 (based on the literature); the literature must be based on the twist boat conformer of isomer 17.

Isomer 18

DOI:10042/26149

Chair

The isomer of another intermediate that is related to Taxol, isomer 18, was minimised using the MMFF94s mechanics force field; the total energy of the minimised structure is 100.551 kcalmol^-1.

18 chair

Energy Term	Value (kcalmol-1)
Total van der Waals energy	49.615
Total Torsional Energy	9.740
Total Angle Bending Energy	30.695
Total Bond Stretching Energy	15.055
Total Electrostatic Energy	-6.095
Total Out-Of-Phase Bending Energy	0.887
Total Stretch Bending Energy	0.653

Thermodynamics

Energy Term	Value (Hartree/particle)
Zero-point correction	0.468
Thermal Correction to Energy	0.489
Thermal Correction to Enthalpy	0.490
Thermal Correction to Gibbs Free Energy	0.421
Sum of electronic and zero-point energies	-1651.417
Sum of electronic and thermal energies	-1651.395
Sum of electronic and thermal enthalpies	-1651.394
Sum of electronic and thermal free energies	-1651.463

Twist Boat

18 boat

Energy Term	Value (kcalmol-1)
Total van der Waals energy	51.717
Total Torsional Energy	12.996
Total Angle Bending Energy	31.735
Total Bond Stretching Energy	15.560
Total Electrostatic Energy	-6.933
Total Out-Of-Phase Bending Energy	0.842
Total Stretch Bending Energy	0.587

The total energy of the minimised structure is 106.505 kcalmol^-1.

Summary

The free energy, ΔG, can be sued to compare the relative energies of isomer 17 and isomer 18. Isomer 18 has a lower free energy than isomer 17, which has a free energy of -1651.453 Hartree/particle, as opposed to -1651.463 Hartree/particle (for isomer 18). Isomer 18 is the most stable isomer, this is because the carbonyl bond is anti (endo) to the "bridge head".

Analysis of the properties of the synthesised alkene epoxides

Catalyst 21 (NELQEA01)

Catalyst 21

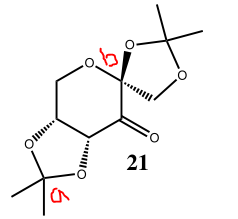
21

The average C-O distances for the anomeric centre (a) is 1.442 Å and the average C-O distance for the anomeric centre (b) is 1.419 Å. The O-C-O bond angle that corresponds to the anomeric centre (a) is 105.78°, this bond angle is less than ideal tetrahedral bond angle of 109.5° because the O-C-O fragment is a part of a five-membered ring; the O-C-O bond angle that corresponds to the anomeric centre (b) is 113.26°, this bond angle is greater than ideal tetrahedral bond angle of 109.5° because the O-C-O fragment encompasses two different ring structures within the catalyst.

Catalyst 23 (TOVNIB02)

23

The closest approach of the two adjacent t-butyl groups on the rings is 2.363 Å (this is almost equal to double the Van der Waals radius of a hydrogen - which is 2.40 Å); the Van der waals radius is double the distance of closest approach between two non-bonded atoms (of the same element) that are merely colliding with one another without reacting to form a bond. Because of the fact that the two hydrogens are within double the Van der Waals radius, the hydrogens can interact with each other (in a Van der Waals fashion) - this stabilises the molecule.

Trans-β-methyl styrene

(ß-methyl styrene‎)

Energy Term	Value (kcalmol-1)
Total van der Waals energy	14.325
Total Torsional Energy	2.895
Total Angle Bending Energy	1.736
Total Bond Stretching Energy	1.886
Total Electrostatic Energy	3.040
Total Out-Of-Phase Bending Energy	0.002
Total Stretch Bending Energy	-0.764

The total energy is 23.120 kcalmol^-1

¹H NMR of Trans-β-methyl styrene oxide

DOI:10042/26182

The ¹H NMR was generated using a B3LYP level of theory, with 6-31G(d,p) as the basis set. The experimentally generated NMR values for each of the protons are tabulated below:

A Gaussview image of the optimised Trans-β-methyl styrene oxide molecule, with all of the atoms numbered.

This is the predicted ¹H NMR spectrum of Trans-β-methyl styrene oxide, using tetramethylsilane (in chloroform) as a reference.

δ (CHCl₃)

Proton	Chemical shift (ppm)
18-H	0.72
19-H	1.59
20-H	1.68
17-H	2.79
16-H	3.41
14-H	7.31
12-H	7.42
11-H	7.48
13-H	7.50
15-H	7.50

Literature values

1H NMR
δ (CDCl3, 400 MHz)
7.24–7.39 ppm	m	5 H
3.57	(d, J=4.3 Hz)	1 H
3.32–3.40 ppm	m	1 H
1.45 ppm	(d, J=5.4 Hz)	3 H

The NMR coincides well with the ¹H NMR that is reported in the literature; the decision of not including the couplings for the generated ¹H NMR was made because it takes ~37 hours for the High-performance computer to generate it.

18-H, 19-H and 20-H are methyl protons; their average chemical shift is 1.33 ppm. The three methyl protons couple with proton 17 to create a doublet peak. 17-H couples with the methyl protons and 16-H to create a doublet of quartets peak. 16-H couples with proton 17-H to create a doublet peak. 14-H, 12-H, 11-H, 13-H and 15-H are the phenyl protons.

¹³C NMR of Trans-β-methyl styrene oxide

This is the predicted ¹³C NMR spectrum of Trans-β-methyl styrene oxide, using tetramethylsilane (in chloroform) as a reference.

δ (CHCl₃)

Carbon	Chemical shift (ppm)
9-C	18.84
7-C	60.58
8-C	62.32
4-C	118.49
2-C	122.73
6-C	122.80
1-C	123.33
3-C	124.07
5-C	134.98

Literature values

13C NMR
δ (CDCl3, 100 MHz)
138.84 ppm
128.30 ppm
127.70 ppm
125.70 ppm
59.70 ppm
59.70 ppm
18.10 ppm

The chemical shifts for the generated ¹³C NMR is similar to the chemical shifts that are quoted in the literature. The main difference between the two NMR is that the generated NMR gives 9 signals, instead of 7 signals. The reason 4-C is magnetically different from 6-C and why 3-C is magnetically different from 1-C is - again - because the Gaussian calculation uses a static structure to model the isomer, rather than a dynamic one; the (5-)C-C(-7) bond isn't rotating in the static model.

Absolute configuration

The VCD spectrum of the (S,S) enantiomer. DOI:10042/26417

The VCD spectrum of the (R,R) enantiomer. DOI:10042/26416

The estimated optical rotation for the (S,S) enantiomer is 46.77 degrees. DOI:10042/26208

The literature value for the (R,R) configuration (at a wavelength of 589 nm, room temperature, and using chloroform as solvent) is -41.8 degrees. This means that the expected value for the optical rotatory power of the (S,S) configuration is 41.8 degrees; 46.77 degrees is reasonably close to this value. The estimated optical rotation for the (R,R) enantiomer is 104.42 degrees, this is not close to the above literature value; optical rotation is highly sensitive. DOI:10042/26215

The vibrational circular dichroism of the two enantiomers were also recorded and compared with the literature. It can be seen that the two spectra are mirror images of each other (as expected); the enantiomers are indeed enantiomers. Unfortunately, no literature spectra was found for the two spectra.

The ECD (Electronic Circular Dichroism) spectrum of the two enantiomers weren't calculated because it is useless for the epoxides - no appropriate chromophore exists for the epoxides.

Using the calculated properties of transition state for the reaction (Shi epoxidation)

Configuration	Structure	Energy (KJmol-1)
RR-1	Oxygen(-35) coordinates to the alkene. ‎	-3.52611x106
RR-2	Oxygen(-35) coordinates to the alkene.	-3.52610x106
RR-3	Oxygen(-43) coordinates to the alkene.	-3.52612x106
RR-4	Oxygen(-40) coordinates to the alkene.	-3.52613x106
SS-1	Oxygen(-35) coordinates to the alkene.	-3.52609x106
SS-2	Oxygen(-35) coordinates to the alkene.	-3.52609x106
SS-3	Oxygen(-39) coordinates to the alkene.	-3.52611x106
SS-4	Oxygen(-39) coordinates to the alkene.	-3.52611x106

The (R,R)- epoxide is the preferred configuration, because it is generally the lower energy configuration, this means that it is the Re face of the alkene is reacted. Oxygen(-43/39/40)] is the oxygen that is used for the transfer. The phenyl group prefers to be anti (endo) with respect to the fructose.

The free energy difference, ΔG, between SS-4 (which is, in fact, slightly lower in energy than SS-3) and RR-4 is -20 KJmol^-1. The equilibrium constant (K), at room temperature, is equal to

$K=e^{-\frac{\mathrm{\Delta }{G}^{\circ }}{RT}}=3190$.

This means that there's a (factor of) 3.2x10³ excess of the (R,R) enantiomer, relative to the (S,S) enantiomer.

The percentage excess of the (R,R) enantiomer is 99.9(7)%; the literature enantiomeric excess (ee) is 88% ee in chloroform, the solvent that was used is water - hence the discrepancy in values between the literature value and the computationally calculated values for the ee.

Using the calculated properties of transition state for the reaction (Jacobsen epoxidation)

Configuration	Structure	Energy (KJmol-1)
SS-1	‎	-8.88276x106
SS-2		-8.88274x106
RR-1		-8.88273x106
RR-2		-8.88273x106

The (S,S)- epoxide is the preferred configuration, because it is generally the lower energy configuration. An exo arrangement of the alkene, in relation to the catalyst, is favoured. The free energy difference, ΔG, between SS-1 and RR-2 is -30 KJmol-1. The equilibrium constant (K), at room temperature, is equal to

$K=e^{-\frac{\mathrm{\Delta }{G}^{\circ }}{RT}}$ = 1.80x10⁵

This means that there's a (factor of) 1.8x10⁵ excess of the (S,S) enantiomer, relative to the (R,R) enantiomer.

The percentage excess of the (S,S) enantiomer is 99.9(9)%; the literature value is 53% ee for the (S,S) configuration. The large discrepancy could be due to the varying conditions between the computational experiment and the experiment as based on the literature.

Transition state analysis (Shi Catalyst)

This is the planar transition state, it leads to the (R,R) enantiomer of trans-β-methyl styrene oxide.

This is the spiro transition state, it leads to the (S,S) enantiomer of trans-β-methyl styrene oxide.

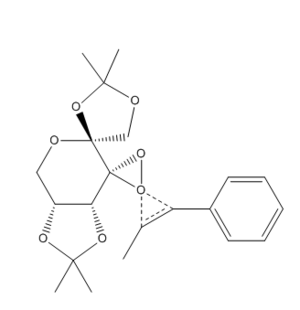
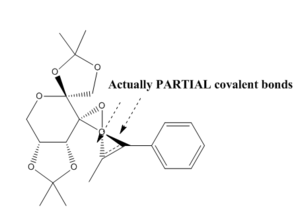
The Shi catalysts has two dioxirane oxygens; the equatorial dioxirane oxygen [oxygen(-39/40/42)] is likely to be sterically more accessible for alkene approach - this leads to the most thermodynamically stable conformation. The reaction of an alkene with the Shi catalyst can produce two types of transition states: a "spiro" transition state or a "planar" transiton state. The literature shows that the epoxidation of trans and trisubstituted alkenes (with the Shi catalyst) proceeds mainly through spiro transition state. In the spiro transition state, the (non-bonding) lone pair of the oxygen is parralel to the π* orbital of the C=C bond - this is a favourable interaction; in the planar transition state, the lone pair of the oxgen is perpendicular to the π* orbital of the C=C bond - the orbitals do not interact. β-methyl styrene has a phenyl group; phenyl groups can lower the energy of the π* orbital of the reacting alkene. The spiro transition state is the sterically favoured transition state because the phenyl group is anti (endo) with respect to the fructose of the Shi catalyst; the phenyl group is syn (exo) with respect to the fructose of the Shi catalyst in the planar transition.

The epoxidation of cis-β-methyl styrene is not as effective as it is for trans-β-methyl styrene because the reaction of cis (and terminal) alkenes with the Shi catalyst can proceed through either one of two distinctive spiro transition states. Because both transition states are spiro, the phenyl and methyl groups of the alkene cannot be differentiated very effectively, thus giving poor enantioselectivity.

QTAIM

The electronic topology of the (S,S)-4 transition state.

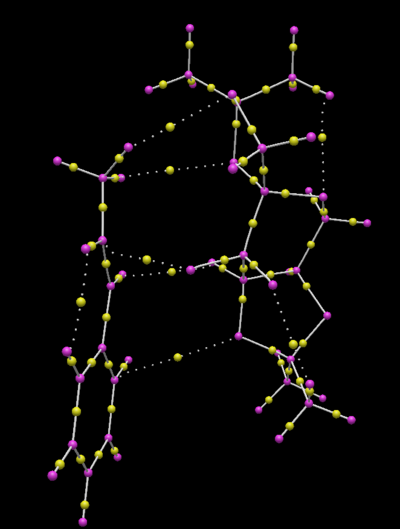
The yellow spheres are bond critical points (BCPs) indicates how the total electron density (within a bond) is distributed between the two constituent nuclei that are forming the bond. From the diagram above, it can be seen that the electron density is exactly half-way between the two carbon nuclei (that bond to form a C-C bond). However, with regards to a C-H bond, cabron has a greater share of the electron density, because carbon is more electronegative than hydrogen. The same logic is also true for oxygen (but to an even greater extent). The dashed lines represent non-covalent (hydrogen or Van der Waals) bonding interactions. Like for the covalent bonding between oxygen and hydrogen, the oxygen has the greater share of the electron density in this non-covalent bonding interaction. Similarly, like a covalent bond between two carbon atoms) the distribution of electron density between two carbon atoms, interacting in a Van der Waals fashion, is equal. There's also a strong, non-covalent, bond between one of the dioxirane oxygens of the Shi catalyst and the double bond from the alkene - this interaction represents the bond-forming interaction that takes place at the transition state.

Investigating the non-covalent interactions in the active-site of the reaction transition state for SS-4 (Shi Catalyst)

It can be seen from this picture that there are some mildly Van der Waals interactions between the hydrogens of adjacent methyl groups. There are also mildly attractive hydrogen bonding interactions between oxygen and a methyl hydrogen. There's a mildly repulsive interaction between the carbons of the phenyl ring. There's a strongly repulsive interaction between the two oxygens in each five-membered ring, due to the strong repulsion of the oxygen lone pair electrons. The multi-coloured ring between (S,S) Trans-β-methyl styrene and the Shi catalyst represents a bond formation in the transition state.

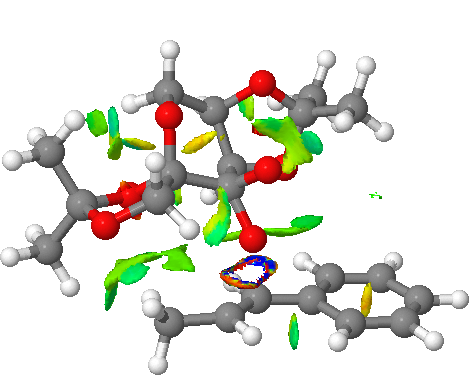
Orbital

Cis-β-methyl styrene

(ß-methyl styrene‎)

Energy Term	Value (kcalmol-1)
Total van der Waals energy	14.545
Total Torsional Energy	2.915
Total Angle Bending Energy	2.173
Total Bond Stretching Energy	1.926
Total Electrostatic Energy	3.037
Total Out-Of-Phase Bending Energy	0.002
Total Stretch Bending Energy	-0.707

The total energy is 23.890 kcalmol^-1

¹H NMR of Cis-β-methyl styrene oxide

DOI:10042/26186

The ¹H NMR was generated using a B3LYP level of theory, with 6-31G(d,p) as the basis set. The experimentally generated NMR values for each of the protons are tabulated below:

A Gaussview image of the optimised Cis-β-methyl styrene oxide molecule, with all of the atoms numbered.

This is the predicted ¹H NMR spectrum of Cis-β-methyl styrene oxide, using tetramethylsilane (in chloroform) as a reference.

δ (CHCl₃)

Proton	Chemical shift (ppm)
18-H	0.69
20-H	0.84
19-H	1.44
17-H	3.28
16-H	3.99
14-H	7.39
12-H	7.46
13-H	7.52
11-H	7.53
15-H	7.55

Literature values

1H NMR
δ (CDCl3, 400 MHz)
7.29 ppm	m	5 H
4.05	(d, J=5.6 H Hz)	1 H
3.33 ppm	(dq, J=7.1, 5.8 Hz)	1 H
1.08 ppm	(d, J=5.4 Hz)	3 H

The NMR coincides well with the ¹H NMR that is reported in the literature. 18-H, 19-H and 20-H are methyl protons; their average chemical shift is 0.99 ppm. The three methyl protons couple with proton 17 to create a doublet peak. 17-H couples with the methyl protons and 16-H to create a doublet of quartets peak. 16-H couples with proton 17-H to create a doublet peak. 14-H, 12-H, 11-H, 13-H and 15-H are the phenyl protons.

The main difference between the proton NMR of Trans-β-methyl styrene oxide and the proton NMR of Cis-β-methyl styrene oxide is the change in chemical shift values (for protons of different environments).

¹³C NMR of Cis-β-methyl styrene oxide

This is the predicted ¹³C NMR spectrum of Cis-β-methyl styrene oxide, using tetramethylsilane (in chloroform) as a reference.

δ (CHCl₃)

Carbon	Chemical shift (ppm)
9-C	13.07
8-C	57.66
7-C	58.99
4-C	121.36
2-C	122.44
6-C	122.71
3-C	123.08
1-C	123.40
5-C	132.81

Literature values

13C NMR
δ (CDCl3, 100 MHz)
135.50 ppm
127.90 ppm
127.40 ppm
126.50 ppm
57.50 ppm
55.00 ppm
12.50 ppm

The chemical shifts for the generated ¹³C NMR is similar to the chemical shifts that are quoted in the literature. The main difference between the two NMR is that the generated NMR gives 9 signals, instead of 7 signals. The reason 4-C is magnetically different from 6-C and why 3-C is magnetically different from 1-C is - again - because the Gaussian calculation uses a static structure to model the isomer, rather than a dynamic one; the (5-)C-C(-7) bond isn't rotating in the static model.

The main difference between the carbon NMR of Trans-β-methyl styrene oxide and the proton NMR of Cis-β-methyl styrene oxide is the change in chemical shift values.

Using the calculated properties of transition state for the reaction (Jacobsen epoxidation)

Configuration	Structure	Energy (KJmol-1)
SR-1	‎	-8.88275x106
SR-2		-8.88273x106
RS-1		-8.88273x106
RS-2		-8.882722x106

The (S,R)- epoxide is the preferred configuration, because it is generally the lower energy configuration. An exo arrangement of the alkene, in relation to the catalyst, is favoured. The free energy difference, ΔG, between SR-1 and RS-1 is -20 KJmol-1. The equilibrium constant (K), at room temperature, is equal to

$K=e^{-\frac{\mathrm{\Delta }{G}^{\circ }}{RT}}=3190$.

This means that there's a (factor of) 3.2x10³ excess of the (S,R) enantiomer, relative to the (R,S) enantiomer.

The percentage excess of the (S,R) enantiomer is 99.9(7)%; ; the literature value is 84% ee (the reaction was run in dichloromethane, hence the discrepancy in values).

Epoxidation of 1,2-dihydronaphthalene

(1,2-dihydronaphthalene)

Energy Term	Value (kcalmol-1)
Total van der Waals energy	19.380
Total Torsional Energy	1.674
Total Angle Bending Energy	2.180
Total Bond Stretching Energy	2.698
Total Electrostatic Energy	5.153
Total Out-Of-Phase Bending Energy	0.009
Total Stretch Bending Energy	-0.870

The total energy is 30.224 kcalmol^-1

¹H NMR of 1,2-dihydronaphthalene oxide

DOI:10042/26184

The ¹H NMR was generated using a B3LYP level of theory, with 6-31G(d,p) as the basis set. The experimentally generated NMR values for each of the protons are tabulated below:

A Gaussview image of the optimised 1,2-dihydronaphthalene oxide molecule, with all of the atoms numbered.

This is the predicted ¹H NMR spectrum of 1,2-dihydronaphthalene oxide, using tetramethylsilane (in chloroform) as a reference.

δ (CHCl₃)

Proton	Chemical shift (ppm)
19-H	1.87
18-H	2.21
21-H	2.27
20-H	2.95
17-H	3.48
16-H	3.56
15-H	7.25
13-H	7.39
11-H	7.39
14-H	7.62

Literature values

1H NMR
δ (CDCl3, 400 MHz)						7.20-7.50 ppm	m	4 H
3.86 ppm	d	1H
3.73 ppm	s	1H
2.85 ppm	dt	1 H
2.55	dd	1 H
2.42 ppm	dd	1 H
1.75 ppm	dt	1 H

The ¹H NMR is very similar to the literature.

¹³C NMR of 1,2-dihydronaphthalene oxide

This is the predicted ¹³C NMR spectrum of 1,2-dihydronaphthalene oxide, using tetramethylsilane (in chloroform) as a reference.

δ (CHCl₃)

Carbon	Chemical shift (ppm)
9-C	29.06
10-C	30.18
7-C	52.19
8-C	52.82
2-C	121.74
6-C	123.53
1-C	123.79
3-C	130.37
5-C	135.39

No literature chemical shifts were found for 1,2-dihydronaphthalene oxide.

Absolute configuration

The VCD spectrum of the (S,R) enantiomer. DOI:10042/26415

The estimated optical rotation (at 589 nm) for the (S,R) enantiomer is 52.76°. DOI:10042/26414

The literature value for the (R,S) configuration (at a wavelength of 589 nm, 20 °C, and using chloroform as solvent) is 129°. This means that the expected value for the optical rotatory power of the (S,R) configuration is -129°; 52.7° is not close to the 129° literature value. It should be noted that optical rotation is also highly sensitive to conformation, and that is A likely reason why there is such a large discrepancy between the literature and the value that was generated.

The vibrational circular dichroism of the conformer was also recorded but, unfortunately, no literature spectra was found for it. The ECD (Electronic Circular Dichroism) spectrum wasn't calculated because it is useless for the epoxides - because no appropriate chromophore exists for the epoxides.

Using the calculated properties of transition state for the reaction (Shi epoxidation)

Configuration	Structure	Energy (KJmol-1)
RS-1	Oxygen(-35) coordinates to the alkene. ‎	-3.62613x106
RS-2	Oxygen(-35) coordinates to the alkene.	-3.62615x106
RS-3	Oxygen(-40) coordinates to the alkene.	-3.62616(7)x106
RS-4	Oxygen(-39) coordinates to the alkene.	-3.62615x106
SR-1	Oxygen(-35) coordinates to the alkene.	-3.62616x106
SR-2	Oxygen(-35) coordinates to the alkene.	-3.62612x106
SR-3	Oxygen(-39) coordinates to the alkene.	-3.62615x106
SR-4	Oxygen(-39) coordinates to the alkene.	-3.62617(3)x106

The (S,R)- epoxide is the preferred configuration, because it is generally the lower energy configuration. Oxygen(-39/40) is the oxygen that is used for the transfer. The phenyl group prefers to be anti (endo) with respect to the fructose.

The free energy difference, ΔG, between SR-4 and RS-3 is -6 KJmol^-1. The equilibrium constant (K), at room temperature, is equal to

$K=e^{-\frac{\mathrm{\Delta }{G}^{\circ }}{RT}}=11.3$.

This means that there's a (factor of) 11.3 excess of the (S,R) enantiomer, relative to the (R,S) enantiomer.

The percentage excess of the (S,R) enantiomer is 91.9% (unfortunately, no literature value was found for the Shi Catalyst).

Suggesting new candidates for investigations

Trans-(2R,3R)-2-(4-methylphenyl)-3-phenyl oxirane.

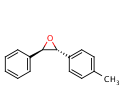
A good candidate would be trans-(2R,3R)-2-(4-methylphenyl)-3-phenyl oxirane; its corresponding alkene is 4-methyl-stilbene, which can be synthesised by reacting 4-methyl-styrene with chlorobenzene (and caesium carbonate and PdCl2(PCy3)2) in 1,4-dioxane. It is a Heck coupling reaction, and it can be done in an undergraduate laboratory - the reaction takes ~12 hours. The optical rotatory power (type M) of trans-(2R,3R)-2-(4-methylphenyl)-3-phenyl oxirane (in ethanol) is -580°, at a wavelength of 436 nm. Trans-(2R,3R)-2-(4-methylphenyl)-3-phenyl oxirane is quite similar (in structure) to (R,R) Trans-β-methyl styrene oxide.