Inorganic Computational Lab

BH₃ Optimization (3-21G basis set)

A Gaussview image of an optimised BH₃ molecule.

The optimised B-H bond distance is 1.19 Å and the optimised bond angle is 120.0 degrees.

This is the 3-21G optimised BH₃ file: opt_bh3

Summary Table

Summary	Results
File name	BH3 Optimisation
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	3-21G
Charge	0
Spin	Singlet
E(RB3LYP)	-26.462 a.u.
RMS Gradient Norm	0.000 a.u.
Imaginary	Freq
Dipole moment	0.00 Debye
Point Group	D3H

"Item" Table


Item                            Value      Threshold          Converged?

 Maximum Force                 0.000413       0.000450             YES

 RMS Force                     0.000271       0.000300             YES

 Maximum Displacement          0.001610       0.001800             YES

 RMS Displacement              0.001054       0.001200             YES

 Predicted change in Energy = -1.071764D-06

 Optimization completed.

 -- Stationary point found.

BH₃ Optimization [6-31G(d,p)basis set]

The optimised B-H bond distance is 1.19 Å and the optimised bond angle is 120.0 degrees.

Summary table

Summary	Results
File name	BH3 Optimisation 631g_dp
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-26.615 a.u.
RMS Gradient Norm	0.000 a.u.
Imaginary	Freq
Dipole moment	0.00 Debye
Point Group	D3H

This is the 6-31G(d,p) BH3 optimisation file: opt_631G_dpbh3

"Item" table

  Item                   Value     Threshold  Converged?

 Maximum Force            0.000017     0.000450     YES

 RMS     Force            0.000011     0.000300     YES

 Maximum Displacement     0.000068     0.001800     YES

 RMS     Displacement     0.000045     0.001200     YES

 Predicted change in Energy = -1.770138D-09

 Optimization completed.

    -- Stationary point found.

GaBr₃ Optimization (LanL2DZ basis set)

A Gaussview image of an optimised GaBr₃ molecule.

Here's the link to the GaBr₃ optimisation in the D-space: GaBr₃ D-space

The optimised Ga-Br bond length is 2.35 Å and the optimised bond angle is 120.0 degrees.

The literature Ga-Br bond length is 2.249 ± 0.005 Å at 638 K, this is reasonably close to the optimised bond length. ^[1]

Summary table

Summary	Results
File name	GaBr3 Optimisation
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	LANL2DZ
Charge	0
Spin	Singlet
E(RB3LYP)	-41.701 a.u.
RMS Gradient Norm	0.000 a.u.
Imaginary	Freq
Dipole moment	0.00 Debye
Point Group	D3H

"Item" table

Item                        Value       Threshold    Converged?

Maximum Force              0.000000      0.000450       YES

RMS Force                  0.000000      0.000300       YES

Maximum Displacement       0.000003      0.001800       YES

RMS Displacement           0.000002      0.001200       YES

Predicted change in Energy = -1.282682D-12  

Optimization completed.

-- Stationary point found.

BBr₃ Optimization (6-31G d,p basis set)

A Gaussview image of an optimised BBr₃ molecule.

This is the 6-31G (d,p) optimised BBr₃ file: opt_bbr3 ‎

The optimised B-Br bond distance is 2.02 Å and the optimised bond angle is 120.0 degrees.

Summary table

Summary	Results
File name	BBr3 Optimisation
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	Gen
Charge	0
Spin	Singlet
E(RB3LYP)	-64.429 a.u.
RMS Gradient Norm	0.000 a.u.
Imaginary	Freq
Dipole moment	0.00 Debye
Point Group	D3H

"Item" table

Item                   Value Threshold Converged?

Maximum Force          0.000008 0.000450 YES

RMS Force              0.000005 0.000300 YES

Maximum Displacement   0.000036 0.001800 YES

RMS Displacement       0.000023 0.001200 YES

Predicted change in Energy = -4.026995D-10

Optimization completed.

-- Stationary point found.

Comparison between BH₃, GaBr₃, and BBr₃

Optimised bond distance (Å)
B-H	Ga-Br	B-Br
1.19	2.35	2.02

What difference does changing the ligand have?

The B-Br bond length is almost twice as large as B-H bond length, this is because Br valence orbital (4p) is much more diffuse than the valence orbital (1s) of H. This means that the overlap between the sp³ orbital of the boron (BH₃ is a dimer) and the 1s orbital of H will be greater than the overlap between the sp² orbital of the boron (BBr₃ is a monomer) and the 4p orbital of Br.

Also, Br is more electronegative than H, which means that the difference in energy between the B and Br orbitals will be larger than the difference in energy between B and H; the closer in energy the overlapping orbitals are to each other the greater the overlap. A larger overlap leads to a larger splitting energy, and larger splitting energies lead to bonding MOs that are lower in energy. This means that the bonding MOs of BH₃ will be lower in energy than the (corresponding) bonding MOs of BBr₃. Bonding MOs that are lower in energy lead to stronger (and shorter) bonds, hence the reason why the B-H bond length is smaller than the B-Br bond length.

In conclusion, a change in ligand can lead to a change in bond length and to a change in geometry (this is explained in the next sub-section).

How are H and Br similar, how are they different?

Similarities: H and Br are both X ligands (a one electron donor ligand). H and Br exist in their diatomic form, H₂ and Br₂ (respectively).

Differences: H only needs two electrons to complete its valence (1s) orbital, Br needs 8 electrons to complete its 4p valence orbital. H can also exist as both an anion and a cation; Br can't exist as a cation. Br has three lone pairs; H has no lone pairs. The reason why BBr₃ can exist as a monomer (but not BH₃) is due to the presence of the lone pairs on Br; Pi-donation from the filled 4p orbitals on Br to the empty 2p orbital on B strengthens the B-Br bond.

What difference does changing the central element make?

The Ga-Br bond length is slightly bigger than the B-Br bond length, this is because GaBr₃ exists as a dimer (whereas BBr₃ exists as a monomer). In GaBr₃, Ga is sp³ hybridised and forms a normal 2e-2c bonds with the terminal Br, and 2e-3c bonds with the bridging Br. The 2e-3c bonds are longer than the normal 2c-2e bonds because the bond order of a 2e-3c bond is 0.5 (compared to a bond order of 1, for a 2c-2e bond). This means that the average Ga-Br bond length will be larger than the average B-Br bond length. The reason why GaBr₃ is a dimer is because the 4p-4p pi overlap between Ga and Br is much weaker than the 2p-4p overlap between B and Br; dimerisation is needed to relieve the electron deficiency in Ga. The B-Br bond length is also stronger (and smaller) due to the 2p-4p overlap.

Also, B is more similar to Br than Ga, in terms of electronegativity. This means that the B orbitals are more similar in energy to the Br orbitals and, therefore, the splitting energy of each overlap (for BBr₃) will be larger than the corresponding orbital within GaBr₃; overlaps with a larger splitting energy yield more stable bonding MOs. Hence, the B-Br bonds should have a shorter bond distance than Ga-Br (and this is, indeed, the case).

In conclusion, a change in the central can lead to a change in bond length and to a change in geometry.

How are B and Ga similar, how are they different?

Similarities: Ga and Br are both group 13 atoms. They both have a similar reactivity. They are both electron deficient in their monomeric (BH₃ and GaBr₃) form.

Differences: B can form stronger bonds with any given ligand.

In some structures gaussview does not draw in the bonds where we expect, does this mean there is no bond? Why?

the reason why gaussview does this is because (like in MO theory) individual electrons are not assigned to individual atoms; the electrons are delocalised around the entire molecule. The bonds are still there, but Gaussview doesn't show them in a 2e-2c fashion.

What is a bond?

A bond is the accumulation of electron density between two atoms/molecules; it is what ultimately attracts two atoms/molecules together. In MO theory, if a bonding MO is (fully) occupied then (unless its corresponding antibonding orbital is also fully occupied there's a bond between the atoms/molecules that contributed (their AOs/FAOs) to the bonding MO.

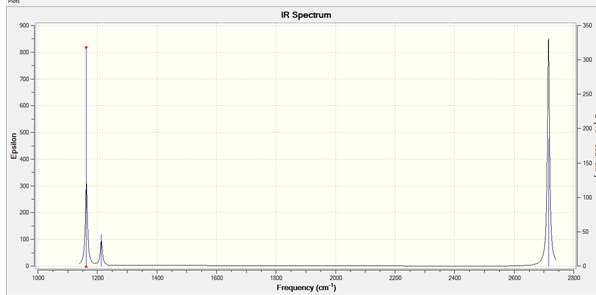
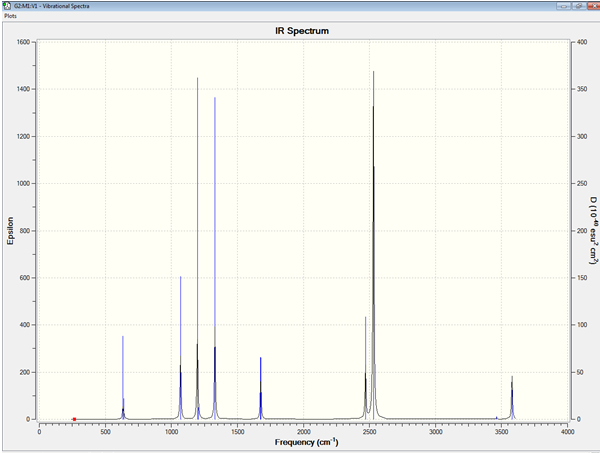
Frequency analysis of BH₃

This is the completed 6-31G(d,p) frequency analysis of BH₃ file: freq_bh3‎

Low frequencies

Low frequencies --- -9 -9 -0 -0 0.5 2.4

Low frequencies --- 1160 1210 1210

"Item" table

Item                         Value       Threshold   Converged?

Maximum Force                0.000017    0.000450      YES

RMS Force                    0.000009    0.000300      YES

Maximum Displacement         0.000068    0.001800      YES

RMS  Displacement            0.000034    0.001200      YES

Predicted change in Energy = -1.779492D-09

Optimization completed.

-- Stationary point found.

Summary table

Summary	Results
File name	FrederickT_BH3_FREQ
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-26.615 a.u.
RMS Gradient Norm	0.000 a.u.
Imaginary	Freq
Dipole moment	0.00 Debye
Point Group	D3H

Vibration table

Number	Form of vibration	Frequency	Intensity	Symmetry label
1	The boron and the three hydrogen atoms are wagging in and out of the plane (B is oscillating in the opposite direction to the three H atoms). ‎	1160	93	A2"
2	The three hydrogen atoms are all scissoring (in the plane of the page); the boron is stretching in the plane of the page.	1210	14	E'
3	Two hydrogen atoms are scissoring; the boron and the remaining hydrogen are stretching in the same dirctions (in the plane of the page).	1210	14	E'
4	The three hydrogen atoms are stretching symmetrically; the boron atom is stationary.	2580	0	A1'
5	Two hydrogens are stretching asymmetrically, the remaining hydrogen is stationary; the boron is stretching in the plane of the page.	2720	126	E'
6	Two hydrogens are stretching symmetrically with respect to each other; the boron and the remaining hydrogen are stretching asymmetrically with respect to each other.	2720	126	E'

IR spectrum

‎

Why are there less than six peaks in the spectrum?

There are two degenerate (E') vibrational modes (at 1210 and 2720 cm^-1, respectively); the two degenerate vibrational modes appear as one peak. Only vibrational modes that lead to a net change in the dipole moment of the molecule absorb infrared radiation, and this is the reason why the A1' vibrational mode doesn't appear in the IR spectrum (it is a totally symmetric mode - it doesn't cause a net change in dipole moment); the IR spectrum only shows the two different degenerate E' vibrational modes and the A2" vibrational mode.

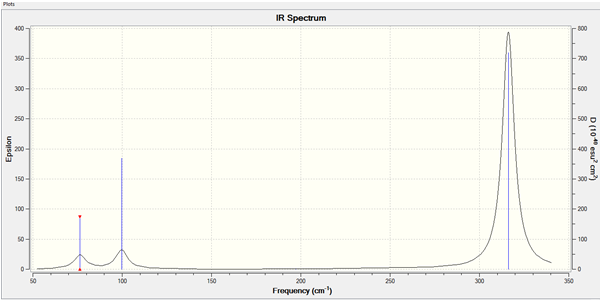
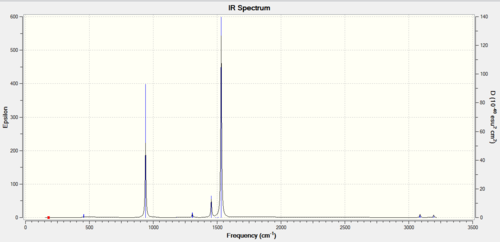
Frequency analysis of GaBr₃

Here's the link to the GaBr₃ D-space that was done for its frequency analysis: GaBr₃ D-space freq

Low Frequencies

Low frequencies --- -1 -1 0 0 0 1

Low frequencies --- 76 76 100

The lowest "real" normal mode is 76 cm^-1.

IR spectrum

Frequency comparison between GaBr₃ and BH₃

Frequency comparison table

BH₃			GaBr₃
Frequency	Intensity	Symmetry label	Frequency	Intensity	Symmetry label
1160	93	A2"	76	3	E'
1210	14	E'	76	3	E'
1210	14	E'	100	9	A2"
2580	0	A1'	197	0	A1'
2720	126	E'	320	57	E'
2720	126	E'	320	57	E'

What does the large difference in the value of the frequencies for BH₃ compared to GaBr₃ indicate?

The large difference in frequency values indicates that the Ga-Br bond length is different to the B-H bond length. The 1s-(2)sp³ overlap between H and B is greater than the 4p-(4)sp³ overlap between Br and Ga (both BH₃ and GaBr₃ are dimers). Bond length and bond strength are inversely proportional. The reduced mass of GaBr₃ is larger than the reduced mass of BH₃. The equation that is used for bond frequency is

$\frac{1}{2 π} \sqrt{\frac{k}{μ}} .$

Where $μ$ is the reduced mass of the system and $k$ is the bond strength.

Has there been a reordering of modes?

Yes, there has been a reordering;

the lowest "real" mode for BH₃ is the mode with the frequency label A2", in contrast to GaBr₃ - its lowest "real" mode has a frequency of 76 cm^-1, this is an E' vibrational mode.

How are these spectra similar?

Both spectra have three peaks (despite the fact that GaBr₃ and BH₃ both show 6 different forms of vibrations).

For both spectra two modes lie fairly closely together, the A2" and E' modes and then the other two modes also lie fairly close together, the A1' and E' modes, but higher in energy. Why is this?

The A" and E' modes are similar in frequency (in both spectra). Quantum mechanically, the energy states for each normal mode is given by

$E_{n} = h (n + \frac{1}{2}) ν .$

The above equation shows that frequency is proportional to energy, hence the reason why the A2" and E' modes lie fairly close together; the A1' and E' have similar frequencies for the exact same reason.

Why must you use the same method and basis set for both the optimisation and frequency analysis calculations?

Because the frequency analysis is also used to confirm that the structure of the optimised molecule is a minimum (on the potential energy surface of the system); if the basis set and the method are not exactly the same then the frequency analysis of the molecule will not be able to confirm this.

What is the purpose of carrying out a frequency analysis?

The frequency analysis is used to predict the IR spectrum of the molecule, to explain why some peaks are not present, to find out the symmetry label of each form of vibration, and to confirm that the structure of the optimised molecule is a minimum (a frequency analysis is essentially the second derivative of the potential energy surface).

What do the "Low frequencies" represent?

The different motions of the center of mass of the entire molecule give rise to the frequencies shown on the first line of the "low frequencies" section; the centre of mass is larger than the reduced mass of the system, hence the low frequencies:

$ν c o m = \frac{1}{2 π} \sqrt{\frac{k}{M c o m}}$

The second line shows the (three) forms of vibrations that have lowest frequencies.

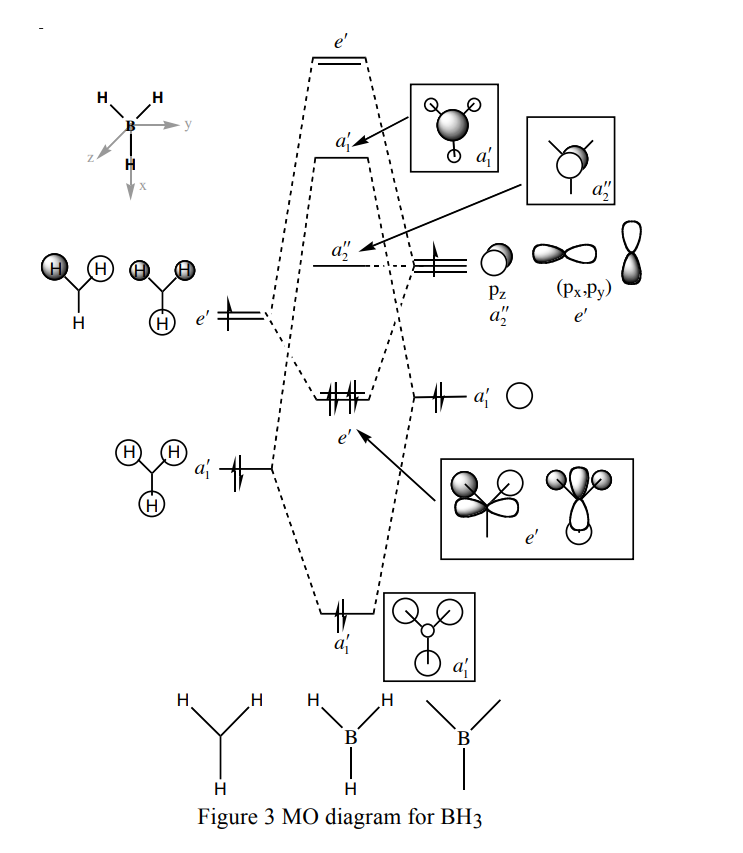
Molecular orbitals of BH₃

Are there any significant differences between the real and LCAO MOs?

There are no significant differences between the real and the LCAO MOs; the relative energy of each MO, and the relative coefficients of the fragment orbitals that make up each of the MOs, were predicted correctly using qualitative MO theory. It should be noted that, unlike LCAO MOs, real MOs combine the AOs on different centres; the LCAO MOs show the individual AO components.

What does this say about the accuracy and usefulness of qualitative MO theory?

Qualitative MO theory is very useful in accurately predicting the MOs of simple molecules.

NBO Analysis of NH₃

This is the 6-31G(d,p) NH₃ optimisation file: NH3_opt. This the 6-31G(d,p) NH₃ frequency file: NH3_freq. And this the 6-31G(d,p) NH₃ MO file: NH3_energy

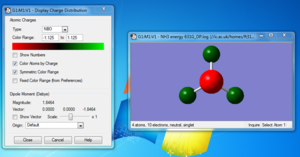
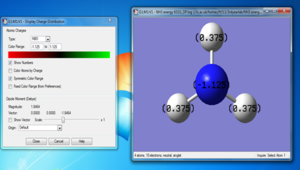
Summary table

Summary	Results
File name	NH3 OPTIMISATION 631G_DP
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-56.558 a.u.
RMS Gradient Norm	0.000 a.u.
Imaginary	Freq
Dipole moment	1.85 Debye
Point Group	C3V

"Item" table

Item                Value  Threshold Converged?

Maximum Force        0.000005 0.000450 YES

RMS Force            0.000003 0.000300 YES

Maximum Displacement 0.000010 0.001800 YES

RMS Displacement     0.000007 0.001200 YES

Predicted change in Energy = -7.830712D-11

Optimization completed.

-- Stationary point found

Low frequencies

Low frequencies --- -12 -12 0 0 0 26
Low frequencies --- 1090 1690 1690

Association energies: Ammonia-Borane

This is the 6-31G(d,p) NH₃BH₃ optimisation file: NH3BH3_opt.

A Gaussview image of an optimised Ammonia-Borane molecule.

Low frequencies

Low frequencies --- 0 0 0 18 23 41
Low frequencies --- 270 630 640

Summary table

Summary	Results
File name	NH3BH3 optimisation
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	6-31G(d,p)
Charge	0
Spin	Singlet
E(RB3LYP)	-83.225 a.u.
RMS Gradient Norm	0.000 a.u.
Imaginary	Freq
Dipole moment	5.57 Debye
Point Group	C1

The point group should be Td.

"Item" table

Item                    Value Threshold Converged?

Maximum Force           0.000128 0.000450 YES

RMS Force               0.000057 0.000300 YES

Maximum Displacement   0.000631  0.001800 YES

RMS Displacement        0.000304 0.001200 YES

Predicted change in Energy=-1.626461D-07

Optimization completed.

-- Stationary point found.

Energy comparison

Energy (a.u.)
BH₃	NH₃	NH₃ BH₃
-26.615	-56.558	-83.225

$Δ E = E (N H 3 B H 3) - [E (B H 3) + E (N H 3)]$ = -0.052.u. = -137 KJ/mol, this is the association energy for combinging a molecule of NH₃ with BH₃.

IR spectrum

Ionic Liquids (Part 1)

Optimisation of [N(CH₃)₄]⁺

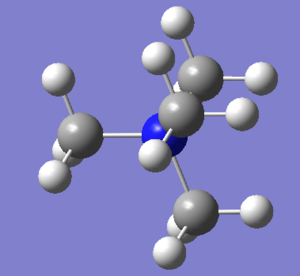
A Gaussview image of an optimised [N(CH₃)₄]⁺ molecule.

The optimised N-C bond length is 1.51 Å and the optimised C-N-C bond angle is 109.5 degrees. N(CH₃)₄ is a tetrahedral cation, and this is confirmed by its bond angle of 109.5 degrees. The optimised C-H bond length is 1.09 Å.

This is the 6-31G(d,p) optimised [N(CH₃)₄]⁺ file: opt_[N(CH₃)₄]⁺. And this is the frequency file: freq_[N(CH₃)₄]⁺.

Summary table

Summary	Results
File name	[N(CH3)4]+_optimisation
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	6-31G(d,p)
Charge	1
Spin	Singlet
E(RB3LYP)	-214.181 a.u.
RMS Gradient Norm	0.000 a.u.
Imaginary	Freq
Dipole moment	0.00 Debye
Point Group	C1

The point group should be T_d.

"Item" table

Item                  Value Threshold Converged?

Maximum Force           0.000107 0.000450 YES

RMS Force               0.000031 0.000300 YES

Maximum Displacement    0.001023 0.001800 YES

RMS Displacement        0.000357 0.001200 YES

Predicted change in Energy = -1.390556D-07

Optimization completed.

-- Stationary point found

Low Frequencies

Low frequencies --- -14 0 0 0 10 23
Low frequencies --- 180 280 290

IR spectrum

Optimisation of [P(CH₃)₄]⁺

The optimised P-C bond length is 1.82 Å and the optimised C-P-C bond angle is 109.5 degrees. P(CH₃)₄ is a tetrahedral cation, and this is confirmed by its bond angle of 109.5 degrees. The optimised C-H bond length is 1.09 Å.

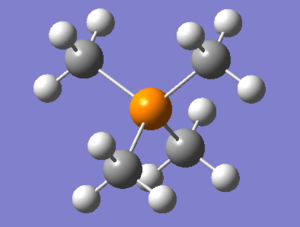
A Gaussview image of an optimised [P(CH₃)₄]⁺ molecule.

This is the 6-31G(d,p) optimised [P(CH₃)₄]⁺ file: opt_[P(CH₃)₄]⁺. And this is the frequency file: freq_[P(CH₃)₄]⁺.

Summary table

Summary	Results
File name	[P(CH3)4]+_OPTIMISATION
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	6-31G(d,p)
Charge	1
Spin	Singlet
E(RB3LYP)	-500.827 a.u.
RMS Gradient Norm	0.000 a.u.
Imaginary	Freq
Dipole moment	0.00 Debye
Point Group	C1

The point group should be T_d.

"Item" table


Item                           Value   Threshold  Converged?
Maximum Force                   0.000073 0.000450   YES
RMS Force                       0.000033 0.000300   YES
Maximum Displacement            0.000808 0.001800   YES
RMS Displacement                0.000269 0.001200   YES
Predicted change in Energy = -2.205226D-07
Optimization completed.
-- Stationary point found.

Low frequencies


 Low frequencies --- -36 -16 -0 06 06 18
 Low frequencies --- 150 190 190

IR spectrum

Optimisation of [S(CH₃)₃]⁺

The optimised S-C bond length is 1.82 Å and the optimised bond angle is 102.7 degrees. S(CH₃)₃ should have a trigonal pyramidal geometry due to the presence of a lone pair on S; the pyramidal bond angle is approximately 107 degrees - 102.7 degrees is clearly shorter than that - the reason for this is because the lone pair is more diffuse than that of any corresponding main group atom (occupying the central position of a molecule). The optimised C-H bond length is 1.09 Å.

A Gaussview image of optimised [S(CH₃)₃]⁺ molecule.

This is the 6-31G(d,p) optimised [S(CH₃)₃]⁺ file: opt_[S(CH₃)₃]⁺. And this is the frequency file: freq_[S(CH₃)₃]⁺.

Summary table

Summary	Results
File name	[S(CH3)3]+_OPTIMISATION
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	6-31G(d,p)
Charge	1
Spin	Singlet
E(RB3LYP)	-517.683 a.u.
RMS Gradient Norm	0.000 a.u.
Imaginary	Freq
Dipole moment	0.97 Debye
Point Group	C1

The point group should be C_3V.

"Item" table


Item                          Value Threshold Converged?

Maximum Force               0.000103 0.000450 YES

RMS Force                   0.000030 0.000300 YES

Maximum Displacement        0.001518 0.001800 YES

RMS Displacement            0.000558 0.001200 YES

Predicted change in Energy=-1.194911D-06

Optimization completed.

-- Stationary point found.

Low frequencies

Low frequencies --- -16 -10 0 0 0 21
Low frequencies --- 150 190 200

IR Spectrum

Molecular Orbitals of [N(CH₃)₄]⁺

Molecular Orbital Number	Number of Nodes	Type of Nodes	Bonding or Antibonding?
16	4	Nodes on each of the carbons.	Bonding.
10	4	Internuclear.	Weakly bonding.
11	4	Nodes on each of the carbons.	Strongly Bonding.
22	4	Internuclear.	Strongly Antibonding.
17	3	Nodes on each of the carbons.	Weakly antibonding.

This is the 6-31G(d,p) energy fchk file: energy_[N(CH₃)₄]⁺.

Ionic Liquids (Part 2)

NBO analysis of [N(CH₃)₄]⁺, [P(CH₃)₄]⁺, and [S(CH₃)₃]⁺

This is the [N(CH₃)₄]⁺ energy log file: energy_[N(CH₃)₄]⁺.

This is the [P(CH₃)₄]⁺ energy log file: energy_[P(CH₃)₄]⁺.

This is the [S(CH₃)₃]⁺ energy log file: energy_[S(CH₃)₃]⁺.

[N(CH₃)₄]⁺			[P(CH₃)₄]⁺			[S(CH₃)₃]⁺
Charge on N	Charge on C	Charge on H	Charge on P	Charge on C	Charge on H	Charge on S	Charge on C	Charge on H
-0.296	-0.483	0.269	1.667	-1.060	0.298	0.917	-0.845	0.279/0.297

Explain the relative contribution of the C and heteroatom to the C-X bond.

The charge difference between P and C (to the C-P bond) is slightly larger than the charge difference between S and C (to the C-S bond), and is noticeably larger than the charge difference between N and C (to the C-N bond). From the NBO analysis, it can be seen that 40.43% of the P-C bond comes from phosphorus and 59.57% comes from carbon. The sp³ orbitals of the phosphorus bonds with the remaining sp³ orbitals from each of the four carbons. The LCAO for the bonding between P and C is

0.636(sp^2.97)P + 0.772(sp^2.96)C.

The LCAO also shows that the carbon contributes more to the P-C bond than phosphorus, because carbon is more electronegative than phosphorus.

It can also be seen, from the NBO analysis, that 48.67% of the S-C bond comes from the carbon and 51.33% comes from sulphur. The LCAO for the bonding between S and C is

0.717(sp^4.86)S + 0.698(sp^4.07)C.

Obviously, sp⁴ and sp⁵ hybridisations don't exist; molecular orbital mixing is the likely reason for the presence of "sp^4.86" and " sp^4.07" hybridised orbitals. Sulphur is only slightly more electronegative than carbon - this explains why the MO mixing is large. MO mixing changes the AO contribution to the (new) MOs, and that is why the hydrogens don't all have the same NBO charge.

It can also be seen, from the NBO analysis, that 66.35% of the N-C bond comes from the nitrogen and 33.65% comes from carbon. The sp³ orbitals of the nitrogen bonds with the remaining sp³ orbitals from each of the four carbons. The LCAO for the bonding between N and C is

0.815(sp^3.00)N + 0.580(sp^3.80)C.

This shows that there's some degree of molecular orbital mixing in [N(CH₃)₄]⁺, but the degree of mixing is a lot smaller for [N(CH₃)₄]⁺ than it is for [S(CH₃)₃]⁺. The LCAO shows that the nitrogen is more electronegative than carbon. Despite the electronegativity difference between N and C is slightly larger than the electronegativity difference between S and C; the NBO charge difference between S and C is a lot larger due to the fact that the degree of mixing is a lot larger for [S(CH₃)₃]⁺. But the charge difference between P and C is so large that even the large molecular orbital mixing in [S(CH₃)₃]⁺ isn't enough for the NBO charge difference between S and C to match the NBO charge difference bwteen S and C.

What does the "formal" positive charge on the N represent in the traditional picture?

A "formal charge" is the electron distribution a particular Lewis structure could have, assuming that the electrons are distributed in such a way that there is perfect covalency. The +1 formal charge represents the fact that the number of groups the nitrogen is bonded to is 1 greater than the number of electrons needed to complete nitrogen's valence shell. The formal charge concept disregards electronegativity completely.

On what atoms is the positive charge actually located for this cation?

The positive charge is actually located on the hydrogens.

Analysis of [N(CH₃)₃(CH₂)OH]⁺

A Gaussview image of an optimised [N(CH₃)₃(CH₂)OH]⁺⁺ molecule.

This is the 6-31G(d,p) optimised [N(CH₃)₃(CH₂)OH]⁺ file: opt_[N(CH₃)₃(CH₂)OH]⁺. And this is the frequency file: freq_[N(CH₃)₃(CH₂)OH]⁺.

Summary table

Summary	Results
File name	[N(CH3)3(CH2OH)]+_OPTIMISATION
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	6-31G(d,p)
Charge	1
Spin	Singlet
E(RB3LYP)	-289.393 a.u.
RMS Gradient Norm	0.000 a.u.
Imaginary	Freq
Dipole moment	1.58 Debye
Point Group	C1

The point group should be T_d.

"Item" table


Item                           Value       Threshold      Converged?
Maximum Force                0.000053      0.000450         YES
RMS Force                    0.000011      0.000300         YES
Maximum Displacement         0.000983      0.001800         YES
RMS Displacement             0.000252      0.001200         YES
Predicted change in Energy=-2.619367D-08
Optimization completed.
-- Stationary point found.

Low frequencies

Low frequencies --- -250 -48 -40 -35 0 0
Low frequencies --- 0 81 190

IR spectrum

Analysis of [N(CH₃)₃(CH₂)CN]⁺

This is the 6-31G(d,p) optimised [N(CH₃)₃(CH₂)OH]⁺ file: opt_[N(CH₃)₃(CH₂)CN]⁺. And this is the frequency file: freq_[N(CH₃)₃(CH₂)CN]⁺.

A Gaussview image of an optimised [N(CH₃)₃(CH₂)CN]⁺⁺ molecule.

Summary	Results
File name	[N(CH3)3(CH2CN)]+_optimisation
File type	.log
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	6-31G(d,p)
Charge	1
Spin	Singlet
E(RB3LYP)	-306.394 a.u.
RMS Gradient Norm	0.000 a.u.
Imaginary	Freq
Dipole moment	5.76 Debye
Point Group	C1

The point group should be T_d.

"Item" table

 Item                               Value       Threshold       Converged?
Maximum Force                     0.000052       0.000450         YES
RMS Force                         0.000009       0.000300         YES
Maximum Displacement              0.001642       0.001800         YES
RMS Displacement                  0.000349       0.001200         YES
Predicted change in Energy=-2.559033D-08
Optimization completed.
-- Stationary point found.

Low frequencies

Low frequencies --- -70 -54 -30 0 0 0
Low frequencies --- 44 110 180

IR spectrum

NBO analysis of [N(CH₃)₃(CH₂OH)]⁺ and N(CH₃)₃(CH₂CN)]⁺

N(CH₃)₃(CH₂CN)]⁺

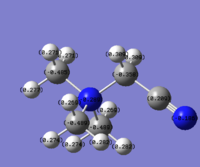
The carbon that is bonded directly to the CN group has an NBO charge of -0.358; the hydrogens of that carbon have each have an NBO charge of 0.241. The central N atom has an NBO charge change from -0.309 (as in [N(CH₃)₄]⁺) to -0.289. The next (two) adjacent carbons have an NBO charge of -0.489; the carbons each have hydrogens with NBO charges of 0.282, 0.274 and 0.269, respectively. The furthermost carbon (with respect to CN) has an NBO charge of -0.489; the hydrogens of that carbon have an NBO charge of 0.277/0.271 (0.277 is the NBO charge of the furthermost hydrogen).

The reason why the carbon that is directly bonded to the very electron withdrawing CN group has the most positive NBO charge is because the (positively charged) central N atom is also (but to a greater extent) electron withdrawing. There's a "tug-of-war" between the central N atom and the CN functional group for the electron density of that carbon atom; the tug-of-war action lessens the electron-withdrawing ability of the nitrogen (with respect to that carbon) - this is also the reason why the NBO charge for the central nitrogen in N(CH₃)₃(CH₂CN)]⁺ is more positive than the NBO charge for the central nitrogen atom in [N(CH₃)₄]⁺. The other three carbon atoms feel the full-effect of the central atom's electron withdrawing ability. The NBO charges of the three non-adjacent carbons are essentially the same (with an NBO charge difference of only 0.001). The 0.001 difference could be due to the fact that the two carbon atoms (with an NBO charge of -0.489) are geometrically closer to the CN functional group - this could also the reason why the the three hydrogens (of each carbon) have different NBO charges; the NBO charge of 0.282 belongs to the hydrogens that are pointing towards the direction of the CN group. The hydrogen atom with an NBO charge of 0.277 is geometrically closer to the CN functional group than the hydrogen atoms with an NBO charge of 0.271.

The expected general trend is that the more negatively charge the carbon should have the less positively charged hydrogens, but this is not always the case because geometrical considerations also need to be taken into account.

This is the energy log file: energy_N(CH₃)₃(CH₂CN)]⁺.

[N(CH₃)₃(CH₂OH)]⁺

‎

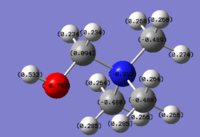
The carbon that is bonded directly to the OH group has an NBO charge of 0.094; the hydrogens of that carbon each have an NBO charge of 0.234. The central N atom has an NBO charge change from -0.309 (as in [N(CH₃)₄]⁺) to -0.313. The next (two) adjacent carbons have an NBO charge of -0.488; the carbons each have hydrogens with NBO charges of 0.285, 0.264 and 0.266, respectively. The furthermost carbon (with respect to OH) has an NBO charge of -0.489; the hydrogens of that carbon have an NBO charge of 0.274/0.268 (0.274 is the NBO charge of the furthermost hydrogen).

The reason why the carbon, that is directly bonded to the very electron withdrawing OH group, has a positive NBO charge is because the (positively charged) central N atom is also (to a much lesser extent) electron withdrawing. There's a "tug-of-war" between the central N atom and the CN functional group for the electron density of that carbon atom; the tug-of-war action significantly lessens the electron-withdrawing ability of the nitrogen (with respect to that carbon). OH is slightly more electron withdrawing than the central nitrogen atom, this is also the reason why the NBO charge for the central nitrogen in [N(CH₃)₃]⁺ is more negative than the NBO charge for the central nitrogen atom in [N(CH₃)₄)]⁺. The other three carbon atoms feel the full-effect of the central atom's electron withdrawing ability. OH is more electron withdrawing than N; unlike in [N(CH₃)₃(CH₂CN)]⁺, it is OH that is the main electron withdrawing group/atom.

OH and the furthermost carbon are antiperiplanar, with respect to each other. This means that the electrons in the O-H σ-orbital is able to interact with the σ*-orbital of the C-H (the two orbitals can overlap efficiently in this conformation). Because of this interaction, the OH group is able to donate more electron-density to the furthermost carbon than it would at a different conformation. This is the reason why the NBO charge of the furthermost carbon is (slightly) more negative than the NBO charge of the other two non-adjacent carbons.

This is the energy log file: energy_N(CH₃)₃(CH₂OH)]⁺

HOMO-LUMO analysis

[N(CH₃)₄]⁺		[N(CH₃)₃(CH₂OH)]⁺		[N(CH₃)₃(CH₂CN)]⁺
HOMO	LUMO	HOMO	LUMO	HOMO	LUMO

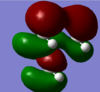
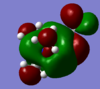
-0.579 a.u.	-0.133 a.u.	-0.466 a.u.	-0.120 a.u.	-0.500 a.u.	-0.182 a.u.

This is the 6-31G(d,p) energy fchk file for [N(CH₃)₃(CH₂CN)]⁺: energy_[N(CH₃)₃(CH₂CN)]⁺. And this is the 6-31G(d,p) energy fchk file [N(CH₃)₃(CH₂OH)]⁺: energy_[N(CH₃)₃(CH₂OH)]⁺.

How has the shape of the orbitals changed?

The LUMO of the three cations are very similar; only the OH and CN parts, of their respective LUMO, are noticably different. The HOMO of the [N(CH₃)₃(CH₂OH)]⁺ and [N(CH₃)₃(CH₂CN)]⁺ cations are noticably different to the HOMO of [N(CH₃)₄]⁺ cation. This is due the presence of the additional functional group; The AO orbital of the central N and the MO orbital of the CH₃ "fragments" are (in general) not high enough in energy to interact with the antibonding MO orbital of the CH₂CN/ CH₂CN fragment. This is the reason why the HOMO of the [N(CH₃)₃(CH₂OH)]⁺ and [N(CH₃)₃(CH₂CN)]⁺ cations (mainly) enclose the CH₂CN region of [N(CH₃)₃(CH₂CN)]⁺ and the CH₂OH region of [N(CH₃)₃(CH₂OH)]⁺, respectively.

The reason why the LUMOs are so similar is because the bonding MO of the CH₂CN/ CH₂CN fragment are too low in energy to significantly contribute to the LUMO of [N(CH₃)₃(CH₂CN)]⁺/[N(CH₃)₃(CH₂OH)]⁺.

Has the energy of these orbitals moved?

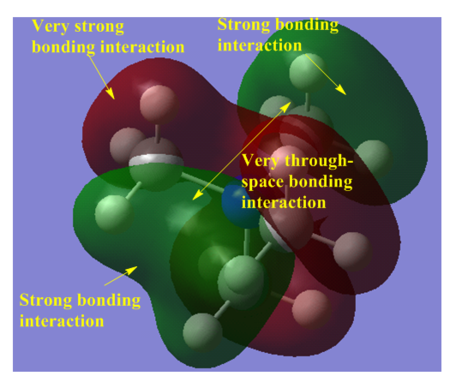
Only slightly - the HOMO, and the LUMO, of the three cations are still similar in magnitude. The HOMO of [N(CH₃)₃(CH₂CN)]⁺ and [N(CH₃)₃(CH₂OH)]⁺ are both higher in energy than the HOMO of [N(CH₃)₄]⁺, this is because the HOMO of [N(CH₃)₃(CH₂OH)]⁺ and [N(CH₃)₃(CH₂CN)]⁺ both have a through-space antibonding interaction, the HOMO of [N(CH₃)₄]⁺ does not.

The LUMO of the [N(CH₃)₄]⁺ cation has a higher energy than the LUMO of the [N(CH₃)₃(CH₂CN)]⁺ and a lower energy than the LUMO of the [N(CH₃)₃(CH₂OH)]⁺ cations. This is because the LUMO of the [N(CH₃)₃(CH₂OH)]⁺ cation has a direct (sigma) antibonding and a through-space antibonding interaction; the LUMO of the [N(CH₃)₃(CH₂CN)]⁺ has a very strong direct (sigma) bonding interaction and a direct (pi) antibonding interaction - the strong sigma bonding interaction is much stronger than the (relatively weak) pi antibonding interaction, and this is the reason why the LUMO of the [N(CH₃)₃(CH₂CN)]⁺ cation is lower in energy than the [N(CH₃)₄]⁺ cation.

Has the HOMO-LUMO gap changed in size?

Yes, the HOMO-LUMO gap of the has changed. The HOMO-LUMO gap for [N(CH₃)₄]⁺, [N(CH₃)₃(CH₂OH)]⁺ and [N(CH₃)₃(CH₂CN)]⁺ are 0.466, 0.346 and 0.318 a.u. (respectively).

What chemical impact could these changes have?

[N(CH₃)₃(CH₂CN)]⁺ is the most reactive (oxidising) cation because it is more able to accept an electron because of the fact that its HOMO-LUMO energy gap is the smallest; the occupation of an electron in the antibonding LUMO is less destabilising for [N(CH₃)₃(CH₂CN)]⁺.

Summary

The data obtained from this project can be explained rigorously by applying the various theories within physical and inorganic chemistry

References

↑ Gallium tribromide: molecular geometry of monomer and dimer from gas-phase electron diffraction

[1] Gallium tribromide: molecular geometry of monomer and dimer from gas-phase electron diffraction

[1]

Inorganic Computational Lab

BH3 Optimization (3-21G basis set)

Summary Table

"Item" Table

BH3 Optimization [6-31G(d,p)basis set]

Summary table

"Item" table

GaBr3 Optimization (LanL2DZ basis set)

Summary table

"Item" table

BBr3 Optimization (6-31G d,p basis set)

Summary table

"Item" table

Comparison between BH3, GaBr3, and BBr3

What difference does changing the ligand have?

How are H and Br similar, how are they different?

What difference does changing the central element make?

How are B and Ga similar, how are they different?

In some structures gaussview does not draw in the bonds where we expect, does this mean there is no bond? Why?

What is a bond?

Frequency analysis of BH3

Low frequencies

"Item" table

Summary table

Vibration table

IR spectrum

Why are there less than six peaks in the spectrum?

Frequency analysis of GaBr3

Low Frequencies

IR spectrum

Frequency comparison between GaBr3 and BH3

Frequency comparison table

What does the large difference in the value of the frequencies for BH3 compared to GaBr3 indicate?

Has there been a reordering of modes?

How are these spectra similar?

For both spectra two modes lie fairly closely together, the A2" and E' modes and then the other two modes also lie fairly close together, the A1' and E' modes, but higher in energy. Why is this?

Why must you use the same method and basis set for both the optimisation and frequency analysis calculations?

What is the purpose of carrying out a frequency analysis?

What do the "Low frequencies" represent?

Molecular orbitals of BH3

Are there any significant differences between the real and LCAO MOs?

What does this say about the accuracy and usefulness of qualitative MO theory?

NBO Analysis of NH3

Summary table

"Item" table

Low frequencies

Association energies: Ammonia-Borane

Low frequencies

Summary table

"Item" table

Energy comparison

IR spectrum

Ionic Liquids (Part 1)

Optimisation of [N(CH3)4]+

Summary table

"Item" table

Low Frequencies

IR spectrum

Optimisation of [P(CH3)4]+

Summary table

"Item" table

Low frequencies

IR spectrum

Optimisation of [S(CH3)3]+

Summary table

"Item" table

Low frequencies

IR Spectrum

Molecular Orbitals of [N(CH3)4]+

Ionic Liquids (Part 2)

NBO analysis of [N(CH3)4]+, [P(CH3)4]+, and [S(CH3)3]+

Explain the relative contribution of the C and heteroatom to the C-X bond.

What does the "formal" positive charge on the N represent in the traditional picture?

On what atoms is the positive charge actually located for this cation?

Analysis of [N(CH3)3(CH2)OH]+

Summary table

"Item" table

Low frequencies

IR spectrum

Analysis of [N(CH3)3(CH2)CN]+

BH₃ Optimization (3-21G basis set)

BH₃ Optimization [6-31G(d,p)basis set]

GaBr₃ Optimization (LanL2DZ basis set)

BBr₃ Optimization (6-31G d,p basis set)

Comparison between BH₃, GaBr₃, and BBr₃

Frequency analysis of BH₃

Frequency analysis of GaBr₃

Frequency comparison between GaBr₃ and BH₃

What does the large difference in the value of the frequencies for BH₃ compared to GaBr₃ indicate?

Molecular orbitals of BH₃

NBO Analysis of NH₃

Optimisation of [N(CH₃)₄]⁺

Optimisation of [P(CH₃)₄]⁺

Optimisation of [S(CH₃)₃]⁺

Molecular Orbitals of [N(CH₃)₄]⁺

NBO analysis of [N(CH₃)₄]⁺, [P(CH₃)₄]⁺, and [S(CH₃)₃]⁺

Analysis of [N(CH₃)₃(CH₂)OH]⁺

Analysis of [N(CH₃)₃(CH₂)CN]⁺

NBO analysis of [N(CH₃)₃(CH₂OH)]⁺ and N(CH₃)₃(CH₂CN)]⁺

N(CH₃)₃(CH₂CN)]⁺

[N(CH₃)₃(CH₂OH)]⁺