Rep:Mod:fp1615 Transition States and Reactivity

3rd Year Transition States and Reactivity Computational Laboratory - session beginning 19th February 2018 - Francesca Pinto

Introduction

In this investigation, the reactivity of different pericyclic reactions was explored computationally by using the PM6 (semi-empirical) and B3LYP (hybrid Density Functional Theory) computational methods. In order to gain an understanding of the reactions being investigated, Gaussian, accessed through the graphical user interface GaussView, was used to locate the stationary points on their potential energy surfaces, and vibrational frequency calculations were carried out to characterise them as minima or transition states.

Potential Energy Surface (PES) and Transition State

A potential energy surface V(r₁,r₂...), is a multi-dimensional plot that describes the variation of potential energy as a function of the relative positions coordinates r_i of all the atoms taking part in the reaction. The potential energy surface of a system of N atoms has the same dimensionality as the number of its geometric degrees of freedom, which are given by the expression 3N-6. A stable structure is located in a local minimum on a PES, whereas a transition state sits in a saddle point. Both local minima and saddle points are defined as stationary points. These points can be mathematically identified by the fact that the first derivative of potential energy with respect to every coordinate r_i must be equal to zero:

$\frac{\partial V(r_i)}{\partial r_i}=0$

A minimum can be distinguished by a saddle point by considering the curvature of the PES around them and thus their second derivatives. In fact, at a minimum point the potential energy increases in all directions, therefore for every r_i:

$\frac{{\partial }^{2}V(r_i)}{\partial r_i^2}>0$

On the other hand, a transition state is located at a saddle point which is characterised by having one negative Hessian eigenvalue (second derivatives are typically written as a matrix called the Hessian). In fact, at a transition state the energy increases in all directions except one in which it decreases (negative Hessian eigenvalue), which corresponds to the reaction path.

The second derivative of potential energy with respect to geometric displacement is the force constant for motion along that geometric coordinate:

$k=\frac{{\partial }^{2}V}{\partial r^2}$

where the frequency of the corresponding vibration is given by $v=\frac{1}{2\pi }\sqrt{\frac{k}{m}}$

As a consequence, the transition state is defined as having one imaginary (negative) vibration that corresponds to the motion of the atoms forming the product, whereas optimised reactants and products that sit in local minima only display positive frequency vibrations. If frequency analysis on the transition state reveals the presence of more than one imaginary frequency it suggests that the structure lies in a higher order saddle point on the potential energy surface.

Nf710 (talk) 19:01, 5 March 2018 (UTC) This was well written and concise well done. the eigenvectors of the hessian matrix are the normal modes. These are linear combination of the degrees of freedom. hence why they look like vibrations when you move along them as a coordinate.

Methods

Gaussian was used for the computations in this investigation, and it was accessed through GaussView, graphical user interface that was also used to visualise the optimised molecular orbitals. The transition states were located and using two methods:

Method 1. A guess transition state is drawn in GaussView using previously optimised fragments. The distances between the atoms involved in the reaction is frozen (2.2 Å for C-C, 2.0 Å for C-O and 2.4 Å for C-S) before optimising the resulting structure to a minimum. Bonds are then unfrozen and the transition state is located using the Berny algorithm and allowing the force to be calculated just once. The obtained structure is confirmed to be a transition state by the presence of an imaginary frequency in the frequency analysis. This method is relatively fast and reliable for small molecules for which TS can be easily guessed.

Method 2. The structure of the product of the reaction is drawn and optimised to a minimum. The distance between the atoms involved in the reaction is then manually altered to values that resemble the transition state (see Method 1) and is then frozen. The resulting structure is optimised to a minimum, bonds are unfrozen and the transition state is located using the Berny algorithm, allowing the force to be calculated just once. Also in this case the obtained structure is confirmed to be a transition state by the presence of an imaginary frequency in the frequency analysis. This method involves more steps than the previous one and can be difficult if the minimum where the optimised product is located is far away in geometry from the TS, but can be said to be more reliable and does not require much knowledge of the transition state so it can be used in more complex systems.

The optimisations were carried out at PM6 level. In the investigation of the reaction between cyclohexadiene and 1,3-dioxole, the structures were first optimised to PM6 level and then optimised to the more accurate, and computationally demanding, B3LYP level, using 6-31G(d) as its basis set.

Parameterised Model 6 (PM6) is a semi-empirical method based on an approximate version of the Hartree-Fock formalism. The two-electron part of the Hamiltonian is not explicitly included in order to reduce computational cost and some experimentally fitted parameters are inserted to make up for the neglected integrals. Calculations carried out using this method are fast, but their accuracy can be limited and if the molecule being computed is not similar enough to the molecules in the database used to parametrize the method they can produce unreliable results.

Density Functional Theory (DFT) is a computational method that derives properties of the molecule based on a determination of the electron density of the molecule, instead of the orbital wavefunction approach that characterises the Hartree-Fork method. The Becke-3 term functional-Lee-Yang-Parr (B3LYP), used in this investigation with the Pople 6-31G(d) basis set, is a DFT-hybrid technique that uses both exchange energies calculated in an exact (Hartree-Fock-like) manner and those obtained from DFT methods in order to improve performance. Although these calculations require more computational (CPU) time, values obtained using this method are comparable to experimental values.

Nf710 (talk) 19:05, 5 March 2018 (UTC) Good understanding here of the methods. you could have included some equations for the Hamiltonians and also explained the basis sets.

Reaction of Butadiene with Ethylene

(Fv611 (talk) Good job across the whole section. Well done!)

Figure 1. Reaction scheme for the Diels-Alder reaction between butadiene and ethylene.

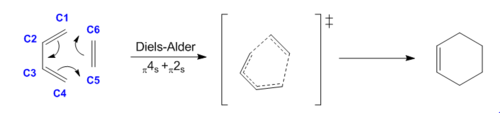
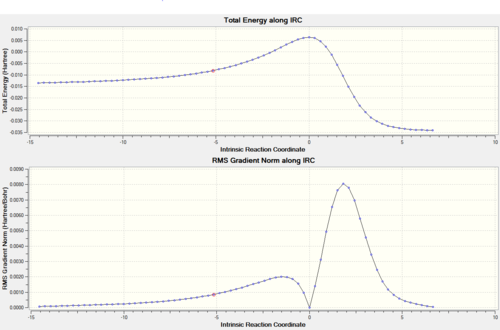
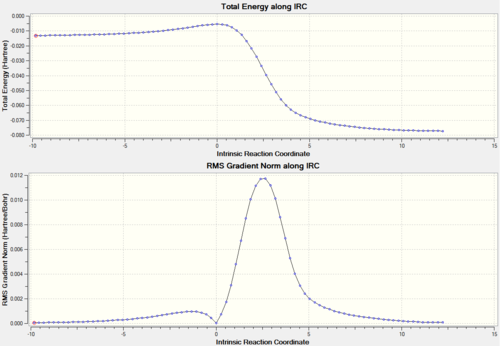
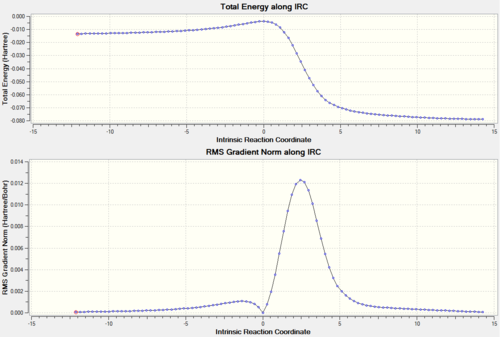
The first pericyclic reaction analysed in this investigation is the Diels-Alder cycloaddition of butadiene (diene) with ethylene (dienophile) to form cyclohexene. This reaction involves a _π4_s and _π2_s component and is thus thermally allowed by the Woodward-Hoffmann rules. The structures of the reactants and of the product were optimised at PM6 level, and the absence of imaginary frequencies in the frequency analysis confirmed that the structures obtained corresponded to minima on the PES. The transition state was located using Method 1 (see Introduction) and optimised at PM6 level; the presence of an imaginary frequency at -948 cm^-1 verified this structure as a transition state. Further evidence for a correct TS was obtained through an Intrinsic Reaction Coordinate (IRC) calculation (Figure 2), which illustrates a successful path from reactants (minimum on RHS) to product (minimum on LHS) through the guessed transition state, the maximum along the minimum energy path. The first derivative of energy of the calculated reaction path is in fact shown to be zero at the reactants, product and transition state.

Figure 2.IRC plot for the reaction of butadiene and ethylene (reactants on LHS, product on RHS).

Figure 3. Animation of the reaction between butadiene and ethylene.

In Figure 3, it is possible to observe an animation of the entire reaction, which clearly demonstrates that symmetry is mantained throughout the reaction and bond forming is synchronous: in fact, the pairs of reacting atoms approach eachother at the same rate and the two new sigma bonds (C4-C5 and C6-C1) are formed at the same time and in one step, in agreement with literature that states that D-A cycloadditions are concerted reactions. The fact that the two ends of butadiene approach ethylene carbons at the same rate in synchronised motion can be further confirmed by observing the imaginary (negative) vibration mode in the transition state (Table 1), which corresponds to the motion of atoms forming the product and thus lowering the energy.

Table 1. Animations of the imaginary frequency and the first real (positive) frequency obtained by frequency analysis of the transition state of the Diels-Alder reaction between butadiene and ethylene.

Imaginary frequency at -948 cm-1

First positive frequency at 145 cm-1

Orbital Description of the Diels-Alder Reaction between Butadiene and Ethylene

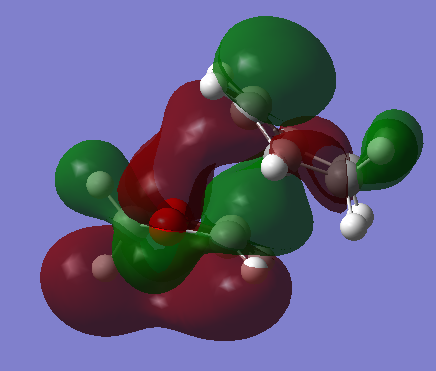
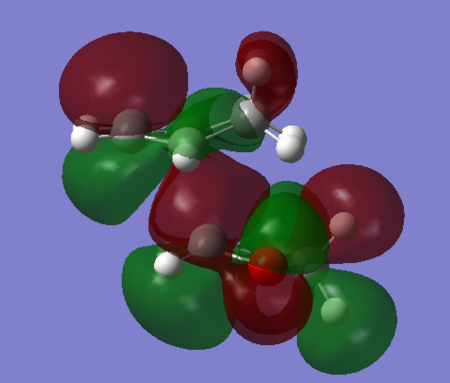
The Jmol applets in Table 2 show the Gaussian-calculated HOMO and LUMO of both butadiene and ethylene as well as the resulting four MOs produced for the transition state. The relative energies of the orbitals of butadiene and ethylene were determined by optimising the structures of reactants that resulted from the IRC calculations on the transition state and subsequently running a single point energy calculation at PM6 level. The MO diagram showed in Figure 4 was constructed using both the molecular orbitals and the energy values obtained using Gaussian. In [4+2] cycloaddition reactions, there is only one persistent symmetry element, a mirror plane, so all molecular orbitals are either symmetric (S) or antisymmetric (A) with respect to it. Analysis of the MO diagram in Figure 4 reveals that the HOMO and LUMO of the transition structure are a result of the interaction between the HOMO of ethylene and the LUMO of butadiene, both of which are symmetric. During a pericyclic process there is a conservation of orbital symmetry, a notion introduced by Woodward and Hoffman, thus the transition state HOMO and LUMO must be symmetric, which can be further confirmed by visual inspection of MOs 6 and 7 in Table 2. Similarly, the antisymmetric HOMO-1 and LUMO+1 of the TS are given by the interaction between the HOMO of butadiene and the LUMO of ethylene, which are both antisymmetric. It can be therefore concluded that only MOs of the same symmetry can interact to form a new bonding/anti-bonding pair. The fact that only symmetric-symmetric (S-S) and antisymmetric-antisymmetric (A-A) orbital interactions are allowed can be rationalised by considering the overlap integral S_AB of the orbitals: in fact, the orbital overlap integral is non-zero for symmetric-symmetric and antisymmetric-antisymmetric orbital interactions, whereas it is zero for interactions of orbitals of the same symmetry.

Table 2. Representation of the HOMO and LUMO of butadiene and ethylene with the corresponding MOs in the transition state.

HOMO of butadiene, corresponding to MO 1 in the MO diagram in Figure 4.	LUMO of butadiene, corresponding to MO 2 in the MO diagram in Figure 4.	HOMO of ethylene, corresponding to MO 3 in the MO diagram in Figure 4.	HOMO of butadiene, corresponding to MO 4 in the MO diagram in Figure 4.
Transition state HOMO-1, corresponding to MO 5 in the MO diagram in Figure 4.	Transition state HOMO, corresponding to MO 6 in the MO diagram in Figure 4.	Transition state LUMO, corresponding to MO 7 in the MO diagram in Figure 4.	Transition state LUMO+1, corresponding to MO 8 in the MO diagram in Figure 4.

Figure 4. MO diagram for the formation of the transition state of the reaction between butadiene and ethylene.

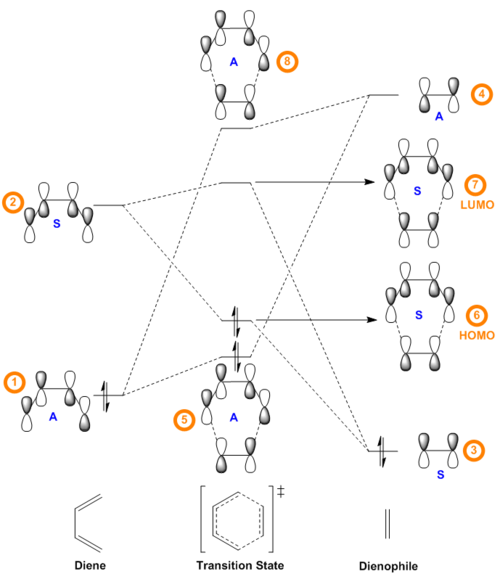
In this reaction, the splitting between the antisymmetric HOMO of butadiene and LUMO of ethylene (0.397 a.u.) is smaller than the splitting between the symmetric LUMO of butadiene and HOMO of ethylene (0.398 a.u.). The HOMO of the diene thus interacts with the LUMO of the dienophile better than the LUMO of diene interacts with the HOMO of the dienophile: the electrons that occupy the HOMO of butadiene populate the LUMO of ethylene, and this cycloaddition can therefore be classified as proceeding with normal electron demand. Lastly, it can be observed that in the MO diagram the energy levels of the TS bonding MOs are higher than what it would be expected in the product: this can be explained by the fact that the TS is located at the highest energy point along the reaction coordinate. The fact that the TS HOMO is closer to the butadiene LUMO than expected can also be seen in its visual representation (MO 6, Table 2): the ethylene HOMO and the butadiene LUMO have in fact almost equal contribution to MO 6 despite the ethylene HOMO being much lower in energy. This effect is less evident in the TS HOMO-1, in which the butadiene HOMO has a much bigger contribution than the ethylene LUMO.

Bond Length Analysis

Careful observation of the reaction scheme in Figure 1 reveals that all the carbon atoms in the reactants are sp² hybridised; the hybridisation of C2 and C3 remains unvaried after the reaction has proceeded to completion, whereas all the other carbon atoms change their hybridisation to sp³ in the product. The values reported in Table 3 show how the different C-C bond lengths change as the reaction progresses through the transition state. In particular, the three double bonds present in the reactants (C1-C2, C3-C4, C5-C6) elongate as the π bonds break and the carbons change hybridisation from sp² to sp³. The fact that these bonds become single C-C bonds in the final product is confirmed by the calculated bond lengths in cyclohexene (1.500, 1.500, 1.540, 1.541, 1.540 Å) adhering strongly to literature values for C-C single bonds (1.536 Å). Similarly, also the bond length values of the newly formed C4-C5 and C6-C1 single bonds agree to literature values. The computed C1-C2 and C3-C4 single bonds in cyclohexadiene are slightly shorter than the other C-C single bonds present in the product of the reaction being investigated. This can be rationalised by analysing the hybridisation of the carbon atoms: in fact, C1-C2 and C3-C4 are both sp³-sp² single bonds (and are equal due to symmetry), while the others are all sp³-sp³ single bonds. In cyclohexene, C2 and C3 have more s-character in the hybridisation and this results in the bonds they form (C1-C2 and C3-C4) being shorter, as s-orbital electron densities are held closer to the nucleus. The C2-C3 single bond present in butadiene (1.471 Å) undergoes the reverse process and shortens to 1.338 Å as it becomes a double bond in the product. Also in this case the formation of this new double bond is confirmed by the computed bond length being comparable to literature values for C=C double bonds.

An analysis of the bond lengths at the transition state of this reaction reveals that the two new bonds that are being formed (C4-C5 and C6-C1) have a length of 2.115 Å and are thus longer than a typical C-C single bond and shorter than twice the carbon atom's Van der Waals' radius (lit. 1.700 Å). This is evidence of the fact that the reacting pairs of atoms, which will eventually form two new sigma bonds, are drawn together and already significantly interacting at this point along the reaction coordinate. Furthermore, the fact that C4-C5 and C6-C1 are equal in the transition state structure further confirms the synchronicity of the reaction as well as the concerted nature of the bond-forming process.

Table 3. Summary of bond lengths for reactants, transition state and product optimised at PM6 level.

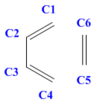	Bond Length (Å)
	Reactants	Transition State	Products
C1-C2	1.333	1.380	1.500
C2-C3	1.471	1.411	1.338
C3-C4	1.333	1.380	1.500
C4-C5	N/A	2.115	1.540
C5-C6	1.327	1.382	1.541
C6-C1	N/A	2.115	1.540
Literature Values	C-C Butadiene = 1.454 ; C=C Butadiene = 1.338 ; C=C Ethylene = 1.330

File links:

Optimised Butadiene (PM6)

Optimised Ethylene (PM6)

Optimised Transition State (PM6)

IRC (PM6)

Optimised Cyclohexene (PM6)

Reaction of Cyclohexadiene with 1,3-Dioxole

Figure 5.Reaction scheme for the Diels-Alder reaction between cyclohexadiene and 1,3-dioxole.

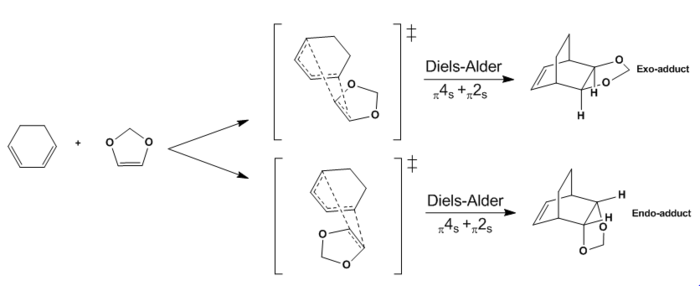
The second reaction analysed in this investigation is the Diels-Alder cycloaddition of cyclohexadiene with 1,3-dioxole. Also in this case the reaction involves a _π4_s and _π2_s component and is thus thermally allowed by the Woodward-Hoffmann rules. However, as it can be observed in the above reaction scheme, two different trajectories of approach in the transition state (ENDO and EXO) result in two different stereoisomers as products.

The transition states of both the ENDO and the EXO Diels-Alder reactions were located using Method 2 and optimised to PM6 and subsequently to the more accurate B3LYP/6-31G(d) level. The presence of imaginary frequencies at -521 cm^-1 (ENDO) and -529 cm^-1 (EXO) verified the structures obtained as transition states. Method 2 involved the optimisation of the products firstly at PM6 and then at B3LYP/6-31G(d) level prior to the formation of the transition states, and the absence of imaginary frequencies confirmed that the structures obtained corresponded to minima on the PES. In addition, the frequency analysis of the optimised structures of the reactants (B3LYP/6-31G(d)) demonstrated that they were also located at a minimum on the potential energy surface. As in the analysis of the previous reaction, for both the ENDO and the EXO D-A further evidence for the correct reactants, products and transition states optimised structures was obtained through an Intrinsic Reaction Coordinate (IRC) calculation (Figures 6 and 8), which illustrated a successful path from reactants (minimum on RHS) to product (minimum on LHS) through the guessed transition state, the maximum along the minimum energy path. In Figures 6 and 8 the first derivative of energy of the calculated reaction path is in fact shown to be zero at the reactants, product and transition state. The IRC calculation was performed on the transition states optimised at PM6 in order to save computational (CPU) time. The animations of the IRC path shown in Figures 7 and 9 clearly illustrate the different approach trajectories for the ENDO and EXO reactions, with the first one favoured by the electronic interaction between the oxygen orbitals on the dienophile and the back of the diene.

Figure 6. IRC plot for the EXO Diels-Alder reaction between cyclohexadiene and 1,3-dioxole (reactants on LHS, product on RHS).	Figure 7. Animation of the EXO Diels-Alder reaction between cyclohexadiene and 1,3-dioxole. The reaction in this case is synchronous and concerted.
Figure 8.IRC plot for the ENDO Diels-Alder reaction between cyclohexadiene and 1,3-dioxole (reactants on LHS, product on RHS).	Figure 9. Animation of the ENDO Diels-Alder reaction between cyclohexadiene and 1,3-dioxole. The reaction in this case is synchronous and concerted.

Orbital Description of the Diels-Alder Reaction between Cyclohexadiene and 1,3-Dioxole

The Jmol applets in the tables below show the Gaussian-calculated HOMO and LUMO of both cyclohexadiene and 1,3-dioxole (Table 4) as well as the resulting four MOs produced for each of the ENDO (Table 5) and EXO (Table 6) transition states. The relative energies of the orbitals of cyclohexadiene and 1,3-dioxole were determined by optimising the reactants that resulted from the IRC calculations on the transition state and running a single point energy calculation at B3LYP/6-31G(d) level. The MO diagrams showed in Figures 10 and 11 were constructed using both the molecular orbitals and the energy values obtained using Gaussian and show the orbitals involved in the formation of both the ENDO and EXO transition state.

Table 4. Representation of the HOMO and LUMO of cyclohexadiene and 1,3-dioxole.

Cyclohexadiene HOMO, corresponding to MO A in the MO diagram in Figures 10 and 11.

Cyclohexadiene LUMO, corresponding to MO B in the MO diagram in Figures 10 and 11.

1,3-Dioxole HOMO, corresponding to MO C in the MO diagram in Figures 10 and 11.

1,3-Dioxole HOMO, corresponding to MO D in the MO diagram in Figures 10 and 11.

Table 5. Representation of the HOMO(-1) and LUMO(+1) of the ENDO Diels-Alder transition state MOs given by the interaction of MOs A-D.

Endo TS HOMO-1, corresponding to MO I in the MO diagram in Figure 10.

Endo TS HOMO, corresponding to MO J in the MO diagram in Figure 10.

Endo TS LUMO, corresponding to MO K in the MO diagram in Figure 10.

Endo TS LUMO+1, corresponding to MO L in the MO diagram in Figure 10.

Table 6. Representation of the HOMO(-1) and LUMO(+1) of the EXO Diels-Alder transition state MOs given by the interaction of MOs A-D.

Exo TS HOMO-1, corresponding to MO E in the MO diagram in Figure 11.

Exo TS HOMO, corresponding to MO F in the MO diagram in Figure 11.

Exo TS LUMO, corresponding to MO G in the MO diagram in Figure 11.

Exo TS LUMO+1, corresponding to MO H in the MO diagram in Figure 11.

Although the MO diagrams in Figures 10 and 11 closely resemble those of the previous exercise because of the fact that the reactants have similarly constructed orbitals and that the MOs of the reactants that have the same symmetry interact to form the TS MOs, the relative energies of the frontier orbitals are now different. In fact, single point energy calculations revealed that the energy difference between the antisymmetric HOMO of cyclohexadiene and the antisymmetric LUMO of 1,3-dioxole (0.242 a.u. endo, 0.234 a.u. exo), which combine to form the antisymmetric TS HOMO-1 and LUMO+1, is bigger than the energy splitting between the symmetric LUMO of the diene and the symmetric HOMO of the dienophile (0.209 a.u. endo, 0.179 a.u.), which interact to form the symmetric TS HOMO and LUMO. It follows that, unlike the previous reaction, the greatest interaction occurs between the LUMO of cyclohexadiene and the HOMO of 1,3-dioxole with electrons flowing from the HOMO of the dienophile to the LUMO of the diene. This reaction can therefore be classified as proceeding with inverse electron demand as a result of the fact that 1,3-dioxole is electron rich and thus higher in energy due to the donation of electron density from the oxygen atoms into its double bond. This is in agreement with literature, which states that Diels-Alder cycloadditions between an all-carbon diene and an hetero-dienophile usually proceed with inverse electron demand. Lastly, also in this case it can be observed that in the MO diagram the energy levels of the TS bonding MOs is higher than what it would be expected in the product: this can be explained by the fact that the TS is located at the highest energy point along the reaction coordinate.

Nf710 (talk) 19:11, 5 March 2018 (UTC) Well done for doing this. It would have been nice to see the orbitals. but well done for investigating this quantitatively.

Figure 10. MO diagram for the formation of the transition state of the ENDO Diels-Alder reaction between cyclohexadiene and 1,3-dioxole.

Figure 11. MO diagram for the formation of the transition state of the EXO Diels-Alder reaction between cyclohexadiene and 1,3-dioxole.

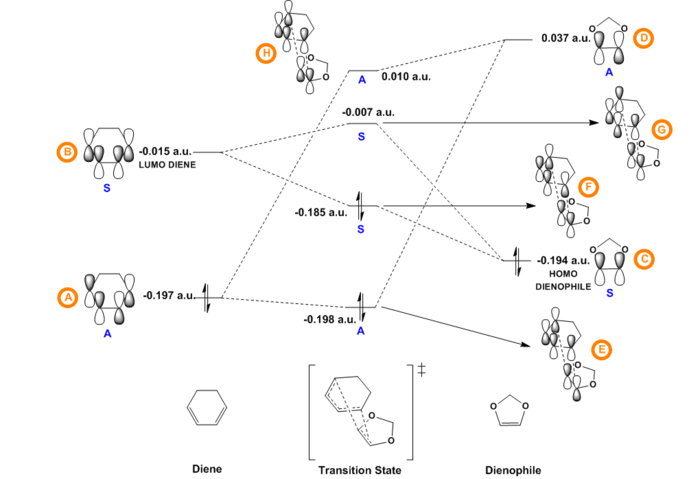
(Fv611 (talk) Excellent MO diagrams)

Thermochemistry Analysis

Despite the fact that the values obtained by optimising the reactants, transition states and products at B3LYP/6-31G(d) are much higher than the corresponding values computed at PM6 level, the relative energies are consistent in both methods. In order to gain a better understanding of the thermochemistry involved in this reaction, the quantitative analysis of activation and reaction energies was carried out using the values extracted from the more accurate calculations at B3LYP/6-31G(d)level.

Table 7. Sum of electronic and thermal free energies (at room temperature) values extracted from the log files of the optimisation of reactants, TS and products at B3LYP level. The conversion factor used was 1 Hartree/particle = 2625.5 kJ/mol.

	Sum of Electronic and Thermal Free Energies
Optimisation Method	Cyclohexadiene	1,3-Dioxole	Reactants	Endo-adduct		Exo-adduct
				TS	Product	TS	Product
PM6 (Hartree/particle)	0.1169	-0.0523	0.0646	0.1379	0.0378	0.1389	0.0380
PM6 (kJ/mol)	306.86	-137.25	169.61	362.17	99.26	364.69	97.71
B3LYP/6-31G(d) (Hartree/particle)	-233.3244	-267.0686	-500.3930	-500.3321	-500.4187	-500.3291	-500.4173
B3LYP/6-31G(d) (kJ/mol)	-612,593.15	-701,188.72	-1,313,781.90	-1,313,622.06	-1,313,849.28	-1,313,614.23	-1,313,845.68

Table 8. Reaction barrier and reaction energy values at room temperature in kJ/mol for both ENDO and EXO Diels-Alder reactions between cyclohexadiene and 1,3-dioxole. These values were calculated using the sum of electronic and thermal free energies extracted from the log files of the optimisation of reactants, TS and products at B3LYP level.

Reaction	Activation Energy (kJ/mol)	Reaction Energy (kJ/mol)
D-A Endo	159.81	-67.37
D-A Exo	167.64	-63.81

Analysis of the values reported in Table 8 reveal that the the endo reaction pathway is the one that possesses the lowest activation energy. Accordingto the Arrenhius equation, which relates the rate of the reaction to its activation barrrier, the lower the activation energy the faster the reaction:

$k=A{e}^{-E_a/(k_{B}T)}$

Nf710 (talk) 19:14, 5 March 2018 (UTC) Well done for discussing the kinetics of the reaction wrt to the arrehnius equation

As a consequence, the endo-adduct forms more rapidly than the exo-adduct and is therefore the kinetically favoured product. This result is in agreement with literature, which also states that under kinetic control (irreversible conditions) the reaction would be stereo-selective towards the endo product. The ENDO trajectory in the transition state of this Diels-Alder cycloaddition is characterised by a smaller reaction barrier because of a stabilising secondary orbital overlap between orbitals that are not involved in the formation of sigma bonds that occurs in the HOMO of the ENDO TS (Figures 12 and 14). The secondary orbital overlap, which lowers the energy of the ENDO TS, consists in the stabilising interaction of the lone pairs located in the p-orbitals of the oxygen atoms with the orbitals located at the back of the diene involved in the development of the new π bond. This overlap does not occur in the HOMO of EXO TS because the oxygen p-orbitals are too far away from the developing double-bond at the back of cyclohexadiene (Figures 13 and 14).

Figure 12. Representation of the HOMO of the ENDO TS with isovalue set to 0.01 to show the secondary orbital overlap between the lone pairs located in the p-orbitals of the oxygen atoms and the p-orbitals located at the back of the diene involved in the development of the new π bond.

Figure 13.Representation of the HOMO of the EXO TS with isovalue set to 0.1 to show the absence of secondary orbital overlap.

Figure 14. Comparative diagram of orbital interactions in the TS HOMO of the Diels-Alder reaction between cyclohexadiene and 1,3-dioxole.

According to literature, the exo-adduct is usually preferentially formed under thermodynamic control (reversible conditions) because it is the most stable (lowest energy) due to the presence of smaller steric hindrance than the the one observed in the endo-adduct. However, in the reaction being investigated the exo-adduct lies higher in energy (and thus has a less negative Gibbs free energy of reaction) than the endo-adduct. This can be rationalised by observing the optimised structures of the products in Figures 15 and 16: visual inspection of the exo-adduct in fact reveals an increased steric hindrance between the heteroatomic 5-membered ring and the bridging carbons. This results in the endo-adduct being both the kinetically and thermodynamically favoured product of the reaction, which would be dominated by the ENDO pathway under both kinetic and thermodynamic control and thus be highly stereoselective towards the ENDO-product.

Figure 15. Representation of the optimised structure of the exo-adduct illustrating the steric clash between the 1,3-dioxole ring and the bridging carbons.

Figure 16.Representation of the optimised structure of the endo-adduct illustrating the much smaller steric hindrance between the 1,3-dioxole ring and the bridging carbons.

File links:

Optimised Cyclohexadiene (PM6)

Optimised Cyclohexadiene (B3LYP/6-31G(d))

Optimised Dioxole (PM6)

Optimised Dioxole (B3LYP/6-31G(d))

Optimised Endo TS (PM6)

Optimised Endo TS (B3LYP/6-31G(d))

Optimised Exo TS (PM6)

Optimised Exo TS (B3LYP/6-31G(d))

Optimised Endo Product (PM6)

Optimised Endo Product (B3LYP/6-31G(d))

Optimised Exo Product (PM6)

Optimised Exo Product (B3LYP/6-31G(d))

Exo IRC (PM6)

Endo IRC (PM6)

Nf710 (talk) 19:17, 5 March 2018 (UTC) This section was excellent well done.

Reaction of Xylylene with SO2: Diels-Alder vs Cheletropic

Figure 17.Reaction scheme for the reaction between o-xylylene and SO₂ illustrating both the Diels-Alder cycloaddition (ENDO and EXO) and the cheletropic pathways.

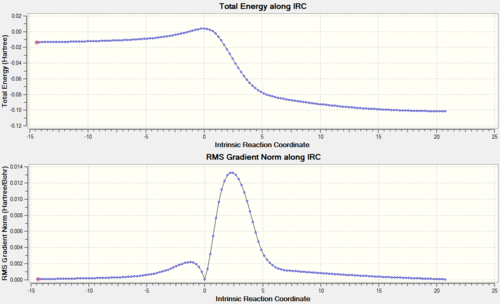
The last reaction analysed in this investigation involves o-xylylene and SO₂. As shown in the reaction scheme above, these two molecules cain either undergo Diels-Alder (ENDO and EXO) or cheletropic cycloaddition. Also in this case both the D-A reactions involve a _π4_s and _π2_s component and are thus thermally allowed by the Woodward-Hoffmann rules.. On the other hand, cheletropic ractions are a subclass of cycloadditions in which the two sigma bonds formed through a cyclic transition state terminate at the same atom (in this reaction sulphur) to form a ring, which in this case is five-membered. The transition states for the above reactions were located using Method 2 and optimised at PM6 level. The optimised structures were confirmed to be at their respective transition states frequency analysis, which for all of them revealed the presence of a single imaginary frequency corresponding to the motion of atoms forming the product. As in the previous exercises, further evidence for a correct TS was obtained through an Intrinsic Reaction Coordinate (IRC) calculation (Figures 18, 20 and 22), which illustrated a successful path from reactants (minimum on RHS) to product (minimum on LHS) through the guessed transition state, the maximum along the minimum energy path. The first derivative of energy of the calculated reaction path is in fact shown to be zero at the reactants, product and transition state. Similarly, the absence of negative frequencies observed in the frequency analysis confirmed that the structures of reactants and products optimised at PM6 level corresponded to minima on the potential energy surface of the reactions that leads to their formation. The animations in Figures 19, 21 and 23 clearly show that in the Diels-Alder cycloadditions the new bonds are formed asynchronously, whereas the bond formation process observed in the cheletropic pathway is synchronous. The asynchronicity observed in the Diels-Alder pathway could be explained by the fact that the reaction involves two different heteroatoms (O and S).

Figure 18. IRC plot for the ENDO Diels-Alder reaction between o-xylylene and SO2 (reactants on LHS, product on RHS).

Figure 19. Animation of the ENDO Diels-Alder reaction between o-xylylene and SO2.

Figure 20. IRC plot for the EXO Diels-Alder reaction between o-xylylene and SO2 (reactants on LHS, product on RHS).

Figure 21. Animation of the EXO Diels-Alder reaction between o-xylylene and SO2.

Figure 22. IRC plot for the cheletropic reaction between o-xylylene and SO2 (reactants on LHS, product on RHS).

Figure 23. Animation of the ENDO Diels-Alder reaction between o-xylylene and SO2.

Thermochemistry Analysis

Table 9. Sum of electronic and thermal free energies (room temperature) values extracted from the log files of the optimisation of reactants, TS and products at PM6 level. The conversion factor used was 1 Hartree/particle = 2625.5 kJ/mol.

	Sum of Electronic and Thermal Free Energies
Species	Units: Hartree/particle	Units: kJ/mol
SO2	-0.1193	-313.13
o-xylylene	0.1788	469.34
Reactants	0.0595	156.21
Terminal D-A Endo TS	0.0906	237.77
Terminal D-A Endo Product	0.0217	59.98
Terminal D-A Exo TS	0.0921	241.74
Terminal D-A Exo Product	0.0214	56.33
Cheletropic TS	0.0990	260.06
Cheletropic Product	-0.000002	-0.0052

Table 10. Reaction barrier and reaction energy values at room temperature in kJ/mol for both the cheletropic and Diels-Alder reactions (ENDO and EXO) between o-xylylene and SO₂. These values were calculated using the sum of electronic and thermal free energies extracted from the log files of the optimisation of reactants, TS and products at PM6.

Reaction	Activation Energy (kJ/mol)	Reaction Energy (kJ/mol)
Terminal D-A Endo	81.56	-96.23
Terminal D-A Exo	85.53	-99.88
Cheletropic	103.85	-156.21

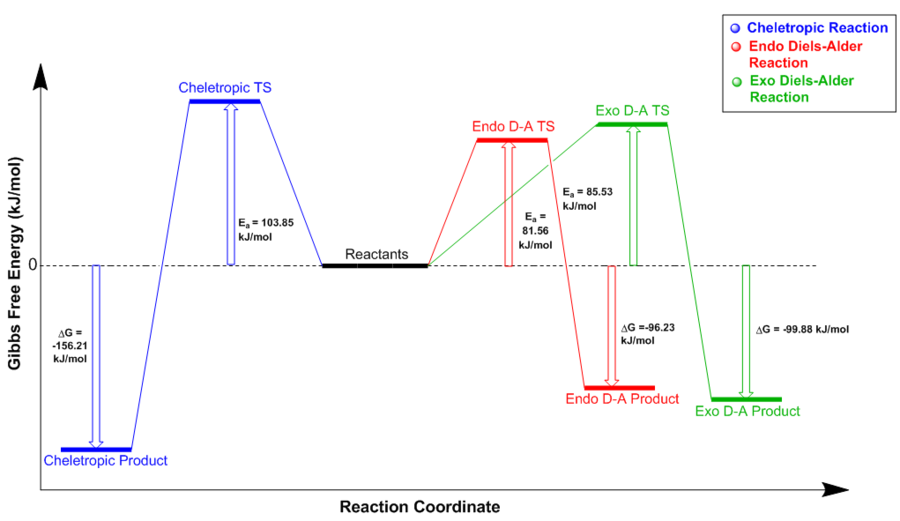
In order to gain an understanding of the thermochemistry involved in this reaction, the quantitative analysis of activation and reaction energies was carried out using the values extracted from the calculations at PM6 level. Analysis of the values reported in Table 10, which are summarised in the reaction energy profiles diagram in Figure 24, reveals that the reaction with the lowest energy transition state and thus smallest activation energy is the ENDO Diels-Alder cycloaddition. The ENDO-adduct is therefore the kinetically favoured product as it forms at a faster rate than the others and it is the predominant product under kinetic control (irreversible conditions). As in the reaction between cyclohexadiene and 1,3-dioxole, the lower reaction barrier can be rationalised by considering the secondary orbital overlap of the π orbital of SO₂ not involved in the formation of the new sigma bonds and the π orbitals located at the back of the diene. In order to gain a better understanding of the secondary orbital overlap occurring in the ENDO TS of this reaction, it would be interesting to compare it to its effect on the Diels-Alder reaction between cyclohexadiene and 1,3-dioxole. However, in order to quantitatively compare the difference in activation energies between the ENDO and EXO pathways for both reactions, it would be necessary to optimise the ENDO and EXO transition state structures for this reaction at B3LYP level.

Despite being characterised by the highest reaction barrier, the cheletropic cycloaddition of o-xylylene and SO₂ has the most negative reaction energy and therefore results in the most thermodynamically stable product (lowest energy). The transition state for this reaction lies at much higher energy than the ones for the Diels-Alder cycloadditions because the formation of a 5-membered ring is more unfavourable than the formation of a 6-membered ring due to smaller bond angles resulting in an increased strain. On the other hand, the adduct formed as a result of the cheletropic reaction is more stable than the ENDO- and EXO- adducts because of the increased stabilisation given by the presence of one more S=O bond.

The above thermochemistry analysis should be repeated using the values obtained from the optimisation of the chemical structures involved at B3LYP/6-31G(d) level in order to verify the accuracy of the calculations at PM6 level. Furthermore, as discussed in the Introduction values obtained using B3LYP/6-31G(d) can be more easily compared to experimental results.

o-Xylylene is an extremely reactive species because it readily undergoes rearrangement in order to increase its stability by becoming aromatic. In this reaction, o-xylylene becomes aromatic in the product, which results in the adducts formed being particularly stable. The aromatisation of the 6-membered ring of this reagent is a strong driving force for all the three reacctions being analysed and can be confirmed by analysis of the IRC calculations: in Figures 19, 21 and 23 it can be observed that as the reaction progresses the existing double bonds slightly lengthen and, at the same time, the initially single bonds shorten. In the final products, all the bonds of the 6-membered ring of o-xylylene have the same length (longer than a C=C double bond, but shorter than a C-C single bond) and are characterised by a bond order of approximately 1.5, which is evidence of aromatisation.

Figure 24. Energy diagram comparing the activation energies and reaction energies of the different pathways for the reaction of o-xylylene and SO₂.

Analysis of Alternative Diels-Alder Pathways

Figure 25. Reaction scheme for the reaction between o-xylylene and SO₂ illustrating the alternative ring Diels-Alder cycloaddition (ENDO and EXO) pathways.

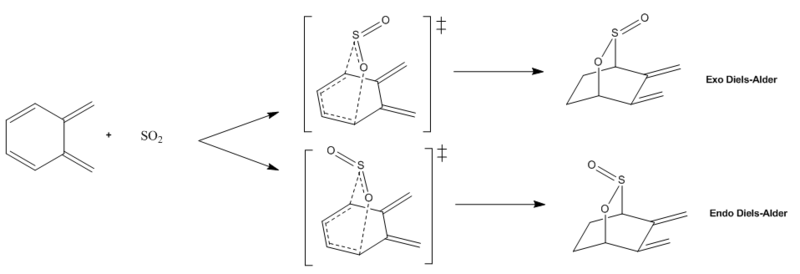
o-Xylylene possesses a second cis-butadiene fragment which is located within its 6-membered ring. As shown in the reaction scheme above, this fragment can also theoretically undergo Diels-Alder cycloaddition with SO₂ resulting in both an ENDO- and an EXO- adduct. The transition states were located and the product were optimised at PM6 level following the same procedure as the one followed for the first part of this exercise. The output of the IRC calculations carried out can be seen in Figures 26-29; in particular, in the animation of the reaction it can be noted that the two new sigma bonds are formed in one step but not at the same time, so both reactions are concerted and asynchronous.

Figure 26.IRC plot for the alternative ring ENDO Diels-Alder reaction between o-xylylene and SO2 (reactants on LHS, product on RHS).

Figure 27. Animation of the alternative ring ENDO Diels-Alder reaction between o-xylylene and SO2.

Figure 28. IRC plot for the alternative ring EXO Diels-Alder reaction between o-xylylene and SO2 (reactants on LHS, product on RHS).

Figure 29. IRC plot for the alternative ring EXO Diels-Alder reaction between o-xylylene and SO2.

Table 11. Sum of electronic and thermal free energies (room temperature) values extracted from the log files of the optimisation of reactants, TS and products at PM6 level. The conversion factor used was 1 Hartree/particle = 2625.5 kJ/mol.

	Sum of Electronic and Thermal Free Energies
Species	Units: Hartree/particle	Units: kJ/mol
Ring D-A Endo TS	0.1021	267.99
Ring D-A Endo Product	0.0656	172.26
Ring D-A Exo TS	0.1050	275.82
Ring D-A Exo Product	0.0673	176.71

Table 12. Reaction barrier and reaction energy values at room temperature in kJ/mol for both the alternative ring ENDO and EXO Diels-Alder reactions between o-xylylene and SO₂. These values were calculated using the sum of electronic and thermal free energies extracted from the log files of the optimisation of reactants, TS and products at PM6

Reaction	Activation Energy (kJ/mol)	Reaction Energy (kJ/mol)
Ring D-A Endo	111.78	16.05
Ring D-A Exo	119.61	20.50

The values reported in Table 12 clearly indicate that the reaction is unlikely to take place at this site. The activation energy values are in fact much larger than in the reaction that involves the terminal cis-butadiene fragment, and the reaction energies are also much lower due to the products formed being less stable. The Gibbs free energy for these reactions is in fact positive, suggesting that there is no thermodynamic driving force for the reaction to take place. This is a result of the fact that aromatisation, which is the main driving force of the cycloaddition at the other site, does not occur in these reactions. Product are less stable (high in energy) due to the lack of the aromatic 6-membered ring. As a consequence, the products formed in these theoretical reaction are not likely to be formed experimentally.

(Good section and well detailed Tam10 (talk) 11:38, 2 March 2018 (UTC))

File links:

Optimised o-Xylylene (PM6)

Optimised SO2 (PM6)

Optimised D-A Endo Transition State (PM6)

Optimised D-A Exo Transition State (PM6)

Optimised D-A Endo Product (PM6)

Optimised D-A Exo Product (PM6)

Optimised Cheletropic Transition State (PM6)

Optimised Cheletropic Product (PM6)

Optimised Alternative D-A Endo Transition State (PM6)

Optimised Alternative D-A Exo Transition State (PM6)

Optimised Alternative D-A Endo Product (PM6)

IRC D-A Endo(PM6)

IRC D-A Exo (PM6)

IRC Cheletropic (PM6)

IRC Alternative D-A Endo (PM6)

IRC Alternative D-A Exo(PM6)

Conclusion

In this investigation, both the semi-empirical PM6 and the hybrid B3LYP methods were successfully used to locate the optimised structures of reactants, products and transition states of different pericyclic reactions, visualise the molecular orbitals involved in them and carry out frequency and thermochemistry analyses. For the reaction of butadiene and cyclohexene, bond length values computed using PM6 were found to be close to experimental values and the orbitals obtained using the same method closely adhered to literature predictions. In order to reduce computational costs, the B3LYP method was only used to perform a detailed quantitative analysis of the reaction between cyclohexadiene and 1,3-dioxole and the results were compared to those obtained using PM6: the many approximations of the latter resulted in very different values from the more accurate DFT-hybrid method, suggesting that PM6 should only be used to generate initial geometries and carry out fast approximate qualitative analyses for small systems. As seen in the first exercise, to some extent PM6 calculations can also be used for a relatively accurate quantitative analysis of very small and simple systems. In a further investigation, it would be suggested to compare the PM6 data to the vales computed using B3LYP also for the other pericyclic reactions analysed. Overall, the simulations performed were found to be useful for a fast qualitative and quantitative description of the reaction systems investigated. In order to assess the accuracy of the predictions, computed vales should be compared to experimental values. However, only relatively straightforward pericyclic reactions were analysed, for which the transition state structure can be easily predicted. The methods used would not be readily applicable to more complex and less familiar systems.