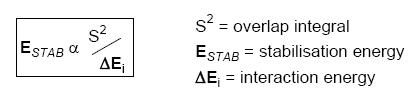Rep:Mod:fleur0909

Modelling using Molecular Mechanics

Introduction

In the following exercise, the method used to calculate the energy and properties of the molecules of interest is molecular mechanics. This technique avoids calculating the exact energy, based on the schrodinger equation, and instead models it. The way it does this is by breaking down the properties of the molecule into five easy to calculate functions that describe the individual bond properties. These are;

The sum of all diatomic bond stretches (calculated from their Hookes law potential).

The sum of all triatomic bond angle deformations (calculated using a Hookes law potential)

The sum of all tetra-atomic bond torsions (a cosine dependance)

The sum of all non-bonded Van der Waals repulsions (calculated using the 6/12 potential).

The sum of all electrostatic attractions of individual bond dipoles.

Known, experimentally derived parameters are used in solving these and they are then summated to give the total energy. This can provide a reasonable approximation for simple organic molecules but does not take electronic factors or orbital overlap into account. As the constants in the equations are experimentally derived, and the equations used to model them are based on the bonds in simple diatomics, this method is limited to simple molecules (usually hydrocarbons). The MM2 program for this kind of modelling was developed by Norman L. Allinger in 1977 and has been subsequently improved. Programs such as MM3(1994) and MM4(2003)have been developed and his research group continues in their strive to develop more accurate and widely applicable computational programs. More information can be found on Allinger's Molecular Mechanics Research Lab's website; http://europa.chem.uga.edu/

The Hydrogenation of Cyclopentadiene Dimer

Using the molecular mechanics techniques outlined above (namely MM2) the relative energies of the endo and exo products resulting from the diels alder dimerisation of cyclopentadiene were calculated using ChemBio3D Ultra.

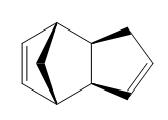
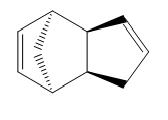
The exdo product shown below is calculated to have an energy of 31.8834 kcal/mol. The endo product has a higher energy of 33.9975 kcal/mol.

Exo	Endo

Examination of the breakdown of the energies , reveals that the torsion and the bend contribute the most. These components represent the strain in the system.This can be rationalised by considering the dihedral angle between the substituents across the new C-C bond. This is much smaller for the endo form, consequently the two double bonds are closer in space and the delocalised pi electron clouds repel each other.

Contributor	Exo	Endo
Torsion	7.6715	9.5039
Bend	20.5870	20.8603
Angle	-178.9	-46.8
Images

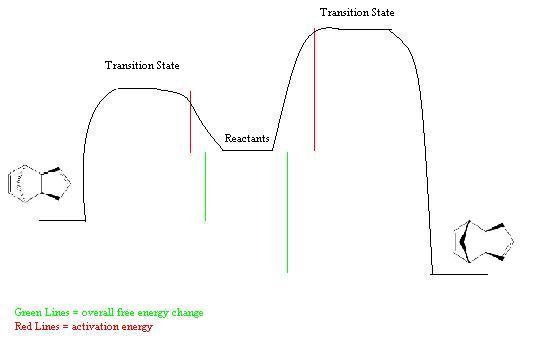
However only the higher energy endo form is formed, indicating that the reaction is not under thermodynamic control. This reaction is known to be under stereoelctronic control, the reaction is a pericyclic [4+2] diels-alder cycloaddition and these are known to be endo selective. This selectivity can be rationalised using the Woodward-Hoffman rules or by Frontier Orbital Theory. In both these theories the transition state leading to the endo product is of a lower energy, hence the reaction is under kinetic control as the endo product has a lower activation energy. This can be seen in the diagram below.

Energy Level Diagram

The MM2 method predicts the wrong major product. This is as the calculations run minimise the energy but don't take into account the reaction paths or transition states that the reaction must proceed via. This limits the number of reactions that this model can be applied to, when wishing to predict the major product of a reaction, as it is only applicible when the reaction is under thermodynamic control.

Dihydro Products

Hydrogenation gives one of the two products shown below.

Molecule 3	Molecule 4

Calculating the energies of molecules 3 (35.9337 kcal/mol) and 4 (31.1540 kcal/mol) reveals molecule 4 to be lower in energy. The main difference in the breakdown of energies is the bend. Molecule 4 has a bend contribution of 14.5074 kcal/mol, wheras in molecule 3 this contribution is much higher, 18.8675kcal/mol. In molecule 4 the angle between the doubly bonded carbons and the substituent is 113 degrees. In molecule 3 the corresponding angle is 107.6 degrees. Thus in both molecules the angle is squashed relative to the ideal 120 degree sp² but much more so in molecule 3. Hence molecule 4 is of lower energy and so based on these calculations would be the product formed, as it is lower in energy than the starting material (which has an energy of 34.0153 kcal/mol) wheras molecule 3 is of higher energy. The reaction is under thermodynamic control.

	Molecule 3	Molecule
Stretch	1.2324	1.0963
Bend	18.8641	14.5074
Stretch-Bend	-0.7625	-0.5493
Torsion	12.2469	12.4972
Non-1,4 VDW	-1.5627	-1.0507
1,4 VDW	5.7523	4.5124
Dipole/Dipole	0.1631	0.1407
Total Energy, kcal/mol	35.9337	31.1540
Angle	107.6	113

Tetrahydro Product

Molecule 5

Formation of the doubley reduced tetrahydro species, molecule 5, does not occur initially and requires much longer reaction times and proceeds at a slower rate, as reported by L.Cerneny, J.Vopatov and V.Ruzika.Calculation of molecule 5's energy reveals it to be 35.2843 kcal/mol, 4.1303kcal/mol higher than the starting material, molecule 4. Hence the second hydrogenation is an endothermic reaction. The main reason for the tetrahydro molecule's high energy is a large increase in the torsion, (17.1462kcal/mol compared to 12.4972kcal/mol).

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)

Example 1

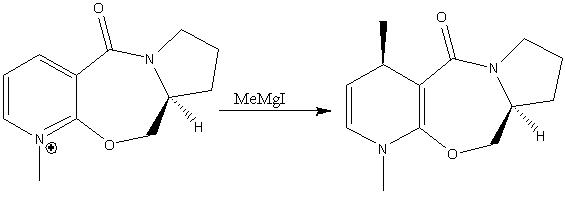
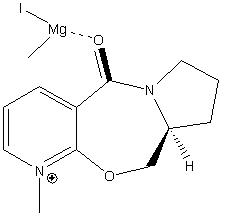
The reaction shown in sceme 1 has been reported by Schultz and Flood as being highly regio- and stereoselective (>99:1). The methyl group ends up on the 4-position, and is always anti with respect to the highlighted hydrogen molecule (attached to the chailral carbon). This behavior can be rationalised using molecular mechanics modelling.

Reaction Scheme 1

The regio- and stereoselectivity of the reaction can be attributed to the gridnard reagent co-ordinating to the carbonyl oxygen, and thus delivering the methyl group to the 4 position exclusively. Attempting to add the IMgMe component into the model results in an error display "WARNING no atom type was assigned to the selected atom!". This is as the MM2 model is based on experimental measurements for well known molecules. The bonds are based on those found in simple diatomics. This model cannot accurately model bonding to metals such as Mg, and hence does not recognise this atom. This is one of the major limitations of the model - it is restricted to simple molecules (best for hydrocarbons) and cannot model co-ordination or anything non classical. The elements recognised by MM2 are carbon, hydrogen, nitrogen, oxygen, sulfur, and halogens and thus modelling is restiricted to molecules containing theese atoms along. The energy of the starting material was minimised using MM2 (from a number of different starting points as this software can get stuck in potential energy wells). This resulted in two possible conformations being returned. The angle is the dihedral angle between the aromatic ring and the carbonyl, with a positive value corresponding to the carbonyl being 'up' with respect to the plane of the plane of the aromatic ring. This has been highlighted in the image of conformer 1 by coulouring the ring yellow for ease of visualisation.

	Conformer 1	Conformer 2
Stretch	0.8899	1.2266
Bend	5.6698	11.5500
Stretch-Bend	0.0885	0.0907
Torsion	9.8995	5.5604
Non-1,4 VDW	-3.0538	-1.8064
1,4 VDW	11.7423	12.0720
Charge/Dipole	3.4329	2.7048
Dipole/Dipole	-3.7379	-3.9270
Total Energy	24.8646 kcal/mol	27.4711 kcal/mol
Image
Dihedral angle	43.7	24.8

The consequence of this is that there is no low energy conformation in which the carbonyl is down with respect to the ring, where down is defined as pointing in the same direction as the hydrogen on the chairal carbon (highlighted yellow in the image of conformer 2). Thus the methyl group is always delivered to the opposite face to this hydrogen, resulting in the stereochemistry shown. The chairal H and new methyl substituent have been highlighted yellow for clarity.

Product

The product energy is detailed in the table below. It is higher than the energy of the reactants. This can be rationalised by considering that the aromaticity of the pyridine ring has been lost. However a quantitive value for how much higher in energy the product is than the reactant cannot be determined from MM2 calculations as the energy values obtained are not absolute values and are best used for comparing isomers or very similar systems rather than products and reactants.

Product
Stretch	0.9793
Bend	8.2776
Stretch-Bend	0.1841
Torsion	12.2
Non-1,4 VDW	-3.1868
1,4 VDW	13.1778
Dipole/Dipole	-3.8916
Total Energy ( kcal/mol)	27.6669
Jmol

Example 2

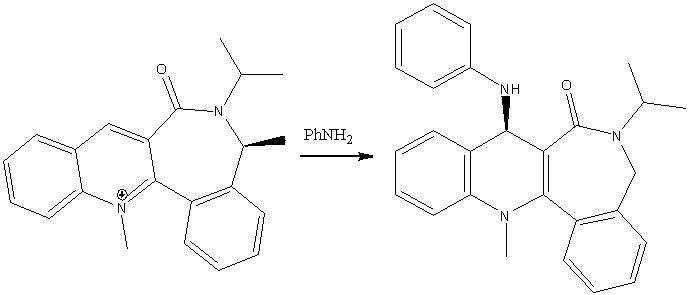
The reaction in scheme 2 also displays a high degree of stereoselectivity (as reported by Leleu et al)and antropenantioselectivity (i.e. addition selectively to one face), so much so that the complexes are known as chairal amide transfer reagents. The same effect has been reported upon reaction with many other nucleophilic groups such as hydrides, enolates (by Ichinose et al. this is especially relevant as it is part of the biosynthesis of vitamin B12) and cyanides (by Kellogg et al). MM2 moddeling was used in order to try to rationalise this behavior and the results are shown below.

Reaction Scheme 2

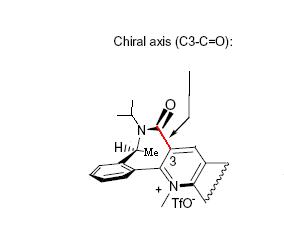
Repeated molecular mechanics modelling calculations, starting from a range of geometries, shows the lowest energy conformation of the reactant to be one possesing an axis of chairality, as highlighted below.

Axis of chairality (2D image adapted from reference 8)

The axis of chairality has been highlighted in purple in the 3D picture, and the methyl group of interest highlighted in yellow.

Reactant energy
Stretch	1.579
Bend	6.8185
Stretch-Bend	0.3364
Torsion	-6.3456
Non-1,4 VDW	-1.8025
1,4 VDW	17.5822
Dipole/Dipole	2.3496
Charge/Dipole	-4.8008
Total Energy ( kcal/mol)	15.7167
Jmol

The incoming nucleophile has a bulky phenyl group attached and thus attacks via the least hindered path, resulting in the stereochemistry shown. The nucleophilic nitrogen also avoids the carbonyl oxygen (thus adding to the opposite face) as both groups possess lone pairs of electrons and thus repel each other. This can be clearly seen in the 3D picture of the product, where the two methyl groups have been highlighted in yellow. Hence the outcome of this reaction is the opposite of the previous.

Product

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Intermediates

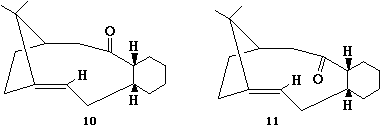
The synthesis of taxol proceeds via one of 10 or 11. In order to predict which isomer is formed MM2 modelling was used to predict the energies of the two possible isomers. Molecule 11, where the carbonyl is pointing up, was modelled from a number of starting points. Originally this gave a very large energy of 120 kcal/mol. I found this to be a rather unrealistic value as it was over twice that obtained for molecule 10. Examination of the structure revealed the cyclohexane unit to be in a boat conformation. Manually changing this in ChemBio3D to a chair conformation and re-calculating gave a much more realistic set of values. Molecule 11 was found to be higher in energy than molecule 10. The breakdown of energies for the lowest energy conformers found for both compounds is shown in the table below.

Energies of 10 and 11

Molecule 11	Result 1	Result 2	Result 3	Result 4	Molecule 10	Result 1	Result 2	Result 3	Result 4
Stretch	2.97	3.02	2.99	3.01	Stretch	2.57	2.56	2.53	2.55
Bend	18.45	18.56	18.46	18.47	Bend	11.8	11.8	11.72	11.73
Stretch-Bend	0.4	0.41	0.4	0.4	Stretch-Bend	0.39	0.38	0.39	0.39
Torsion	20.15	19.98	20.05	19.98	Torsion	18.91	18.87	19.02	18.98
Non-1,4 VDW	-0.72	-0.69	-0.6	-0.54	Non-1,4 VDW	-0.9	-0.76	-0.87	-0.85
1,4 VDW	13.61	13.63	13.62	13.64	1,4 VDW	12.44	12.43	12.45	12.41
Dipole/Dipole	0	0	0	0.01	Dipole/Dipole	0.14	0.14	0.14	0.14
Total Energy ( kcal/mol)	54.86	54.9	54.92	54.97	Total Energy ( kcal/mol)	45.36	45.42	45.39	45.35
Jmol

The major difference between the two structures is the bend energy which is much higher in molecule 11. In molecule 11 the sp² carbonyl carbon has it's substituents placed around it at angles of 119.7 degrees (almost the ideal 120 degrees) wheras in molecule 10, due to the constraints of the cyclic system, this angle is 115.9 degrees. This may account for the increase in bending energy. Another contribution could be that the hydrogen on the adjacent ring carbon in molecule 11 is gauche wheras it is antiperiplanar in 10. This can be seen below where the H of interest has been highlighted green.

Molecule 11	Molecule 10

Hence I would predict that molecule 11 would isomerise to molecule 10 when left standing.

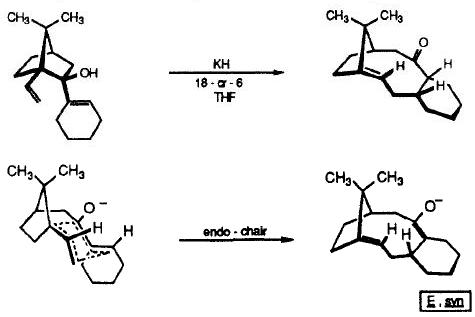
This is consistant with experimental findings published by Paquette et al, who found that when they synthesised the compound of interest, according to the reaction scheme shown, it isomerised to give one product (10). They proposed this went via an endo chair transition state (shown below).

Attack of the carbonyl would occur from the least hindered face so that the nucleophile would end up pointing down (with respect to the bridgehead) in the product.

Double Bond Reactivity

Modelling the product of hydrogenation of 10 and optimising gave an energy of 58.0316 kcal/mol. This is significantly higher than the energy of the reactants. The breakdown of the contributions to the energy shown below reveal that the main reason for this is a large increase in the bend and torsion terms compared to molecule 10. This is because the strained ring system forces the carbons in the 10 membered ring to to adopt angles larger than the ideal 109 degrees for sp³. In the diagram below the two carbons that were doubly bonded have been highlighted yellow. The angles around these carbons are shown shown on the MM2 calculations to be 123.3 degrees and 115.8 degrees. These are much closer to the sp² angles of 120 degrees hence sp² hybridized carbons are less strained in this system.

Product
Stretch	3.5025
Bend	16.9223
Stretch-Bend	0.6077
Torsion	20.6133
Non-1,4 VDW	1.3297
1,4 VDW	15.0560
Dipole/Dipole	0.0000
Total Energy	58.0316 kcal/mol

Molecule 10 can be described as a hyperstable alkene. This concept was introduced by Wilhelm F. Maier, and Paul Von Rague Schleyer. The olefin strain energy (OSE) is defined as the strain energy of the alkene minus the strain energy of the corresponding alkane. This is usually positive (i.e. the cycloalkene is more strained), but for certain ring systems such as the one described above the OSE is negative and the alkene is hyperstable towards hydrogenation.

How one might induce room temperature hydrolysis of a peptide

Peptide hydrolysis

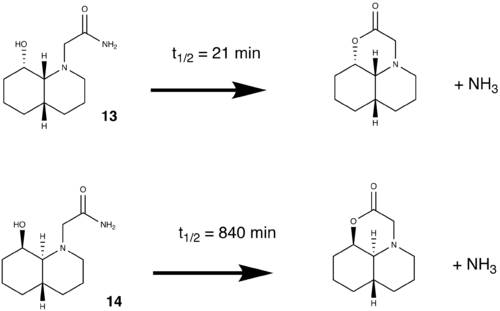
Molecules 13 and 14 were modelled and optimised in an attempt to explain the kinetic behavior reports by Fernandes et al. .

Molecule 13

Optimisation of molecule 13 found it to have two possible low energy conformations, shown below. In both these conformations the ethylamine group is eqitorial and the hydroxyl group is axial. In the lowest energy conformation(a), hydrogen bonding between the carbonyl oxygen and the hydroxyl hydrogen can occur. This is as the distance between them is 1.808 amstrongs (short enough to H-bond) and they can align correctly in space. This fixes the geometry of the molecule and stabilises it. However in this conformation the hydroxyl oxygen cannot approach the antibonding carbon centered antibonding orbital at 109 degrees (the bugi-dunitz angle) and thus this conformation is obviously not the reactive species. In the second conformation(b) hydrogen bonding can occur between a lone pair on the hydroxyl oxygen and the hydrogen on the amine group as they can align in space and are only 1.733 amstrongs apart. The hydroxyl oxygen is 146.2 degrees relative to the plane of the C=O bond. The distance between them is 3.517 amstrongs (close enough to react). Considering that molecules vibrate and are not static, this position is one in which reaction is feasible as the relative position of the hydroxyl group in the ground state is not far from one which allows attack of the carbonyl carbon at 109 degrees.

Molecule 14

Optimisation of 14 also showed two low energy conformations, where the ethylamine group is eqitorial and the hydroxyl group is axial, shown in the table. H-bonding can occur in both conformations as for molecule 13. The slightly higher energy one(14b) was identified as the reacting species, for the same reasons as molecule 13. 14b has an angle between the carbonyl carbon and the hydroxly group of 122.9 degrees (closer to 109 degrees than in 13b) and the distance between them is 3.169 amstrongs (closer than in 13b). Hence based on models of the reactants, one would expect that 14 would have a shorter half life than 13, which does not agree with experimental findings.

	13a	13b	14a	14b
Image
Energy (kcal/mol)	15.5326	19.9038	9.6860	11.7126

Discussion

However the geometries of the starting materials is not the only factor to be considered in these kinetically controlled reactions. The rate of the reaction depends on the energy of the transition state (activation energy). According to Hammonds postulate, the transition state will resemble either the reactant or the intermediate to which it is closest in energy. In an attempt to rationalise the rate of the reactions, the intermediates were modelled and their energies optimised, after ensuring that MM2 could be used to model molecules of this type. The intermediates are rigid structures, held in place by the formation of an additional 6 membered ring, in contrast to the starting materials that can flip and adopt an number or conformations. MM2 optimisation revealed that the intermediate deriving from 13b is 1.3050 kcal/mol lower than that derived from 14b. Additionally 13b is of a higher energy than 14b (see table) so the difference between 13b and its intermediate is smaller than 14b and its intermediate. However the activation energy cannot be predicted from the relative energies of the intermediates and the transition states as it is a kinetic barrier and the molecule may have to undergo a high energy distortion in order to get from one to the other. One may reasonably assume from inspection of the structures in Chemdraw3D that both molecules would have to undergos similar distortions in order to get to their intermediate. Thus the major product can be rationalised by assuming that the transition state resembles the intermediate and hence 13b has a lower activation energy and thus is the major product as this reaction is under kinetic control. This rationalisation however is based on assumptions and does not have a solid theoretical basis as the transition states have not been modelled. This is a limitation of the MM2 method, it cannot be used to model transition states easily. Hence predictions can only be based on relative energies of reactants and products. This means that reactions under thermodynamic control are most suitable as the major product can then be rationalised by consideration of the realtive energies of the products, unlike in kinetically controlled ones where it cannot.

	Intermediate from 13b	Intermediate from 14b
Image
Energy (kcal/mol)	22.1348	23.4402
Jmol

The published literature states that the reason 13 reacts faster than 14 is because when 14 has the ethyl aminde group equitorial it is too far from the hydroxyl group to react, as shown below. This is of course not the case as there is free rotation about the N-C bond and the conformation in which the carbonyl carbon is close to the hydroxyl group is stabilised by hydrogen bonding (as shown in 14a and b).

Modelling Using Semi-empirical Molecular Orbital Theory and Density Functional Approach

Introduction

Semi-empirical Methods

As shown and discussed in the preceeding exercises, MM2 is a rather limited modelling method. In order to incorporate electronic behavior into molecular modelling, semi-empirical methods have been developed.

The method of choice for the following exercise is the Hartree Fock approximation (extended Huckel), using an STO-3G basis set.

This methods uses a linear combination of basis gaussian type functions (of the form -ar²)known as the basis set, to describe the wavefunctions of the molecule (nb the gaussian functions describe the atomic orbitals, i.e. we are using LCAO approximation). The core electrons are not included, only a minimal basis set is used to speed calculations. Some two electron repulsion terms are also omitted. This gives rise to errors which are corrected for by introducing parameters to correlate results to those obtained experimentally or by using ab initio methods which do not omit any terms. Consequently this method works best when the molecules used to define the parameters are similar to those being modelled.

The solutions obtained from the schrodinger equation are then minimised using variational techniques. The energy obtained will always be higher than the real energy (according to the variational theorum. The limiting smallest value to which the calculations converge is known as the Hartree-Fock limit.

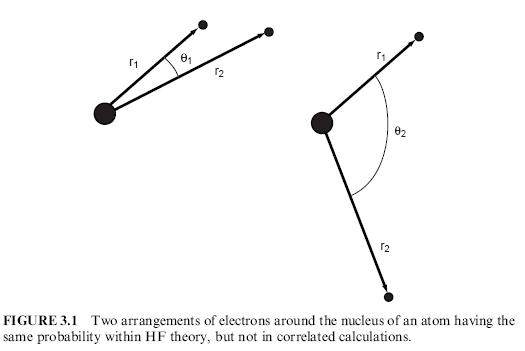
One of the limitations of the HF calculation method is that it calculates the average effect of electron repulsion but doesnt calculate/account for explicit interaction between individual electrons (electron correlation). The result is that conformations where electrons are very close together (high energy due to coulombic repulsions) have the same probability as where they are far apart as long as the r1 and r2 are the same. This is illustrated below. As a consequence the energies calculated are always higher than the true energy.

Illustration (taken from Computational Chemistry: A Practical Guide for Applying Techniques to Real-World Problems)

The approximations used are summarised below, these are the major causes of error/inaccuracy in the resultant models.

1. The Born Oppenheimer approximation

2. Omitting core electrons (incomplete basis set)

3. Central Field approximation (incomplete correlation)

4. The omission of relativistic effects

Despite this semi-empirical methods can give good results for organic molecules geometry, energetics and vibrational modes. Their major advantage is that they have low computational requirements and are relatively fast.

Density Functional Approach

Density functional calculations give more accurate results than semi-empirical ones do (although they take longer and are have higher computational requirements). The DF approach has the advantage of being less computationally demanding than other ab-initio methods that give the same accuracy.

The main difference in DF calculations is that they compute the energy of the molecule from the electron density and not from the wavefunction. So rather than forming a linear combination of atomic orbitals to find the wavefunction, a linear combination of basis functions is used to find the electron density (Kohn-Shan orbitals). This expression is then put into a determinant and the electron density obtained from this is used in subsequent calculations(put into density functionals, in this case B3LYP-Becke 3 term with Lee, Yang, Parr exchange) to find the energy. The accuracy of results depends on the density functional and basis set used.

Regioselective Addition of Dichlorocarbene

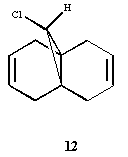
In order to rationalise the reported selectivity of molecule 12 to react with electrophilic reagents (such as dichlorocarbene and peracids) preferrentially on the endo face, the molecule was modelled in ChemBio3D Ultra. Upon inspection one may expect that the exo face would be preferred as this is the least hindered double bond (with respect to attack from the top face at least) and the chlorine is electron rich and thus would serve to attract incoming electrophiles. Clearly the selectivity must be down to other electronic factors. Hence the molecular orbitals of molecule 12 were computed in order to try to find an explination. The geometry of 12 was optimised and energy minimised first by MM2 to give a breakdown of energies shown in the table below.

MM2 Optimised energy of 12

	Molecule 12
Stretch	0.6160
Bend	4.7495
Stretch-Bend	0.0397
Torsion	7.6768
Non-1,4 VDW	-1.0986
1,4 VDW	5.8028
Dipole/Dipole	0.1122
Total Energy	17.8984 kcal/mol
Image
Jmol

It is worth noting at this point that the exo double bond is bent towards the bridging unit. The distance between the bridging carbon and the exo double bond is 2.981 amstrongs, and between the endo double bond is 3.214 amstrongs. As the MM2 method does not take into account the different interacting molecular orbitals this can only be put down to steric factors at this point.

Hartree Fock Optimisation

The geometry was then optimised using the Hartree Fock Semi-empirical method. The energy was -670493.72 Kcal/Mol (obviously the two methods do not give comparable energies). The geometry and bond lengths were not vastly changed, however with the distance between the bridging carbon and a carbon in the exo double bond increased to 3.018 amstrongs(0.039 amstrong increase). The distance to a carbon in the endo double bond was 3.236 amstrongs(decreased). Upon examination of the molecule and given the reported selective reactivity of the endo double bond, the exo distance may be expected to be shortened and the endo one lengthened due to an interaction between the antibonding C-Cl orbital and the C=C pi orbital, as this method considers the MO's in the molecule. However as the two methods use different approximations the results obtained are not quantitavely comparable.

This method calculates the molecular orbitals which can then be visualised in ChemBiodraw3D. These are shown below.

HOMO - 1	HOMO	LUMO	LUMO + 1	LUMO + 2

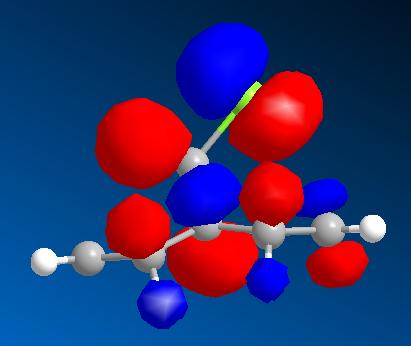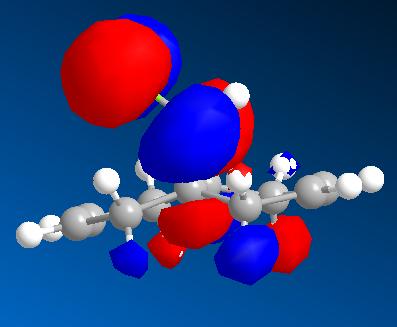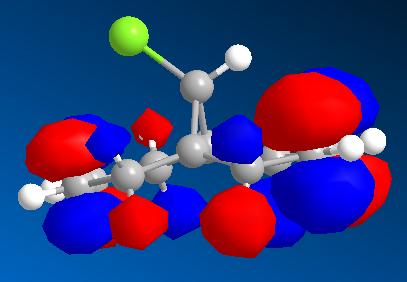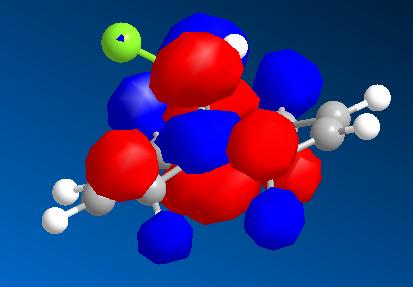
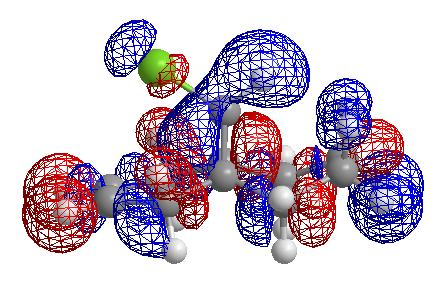
From these pictures it can be seen that in the LUMO the exo double bond has a larger antibonding orbital than the endo double bond, implying it would be more suceptible to nucleophilic attack (as the molecular orbital is normalised the two relative sizes can be compared within it). The HOMO has a large antibonding C-Cl component, implying that this bond is weaker than a simple C-Cl bond.

Density-functional model

The energy was reported as being -877.134152 a.u. (again cannot really compare to other two energy results). The distance from a carbon in the endo double bond and the bridging carbon was found to be 3.28425 amstrongs and from the exo double bond 3.02938 amstrongs. This is a further increase in endo decrease and increase in exo distance. Hence as the quality of the model is improved with respect to taking electronic factors into account, the distance between the bridgehead carbon and the exo carbon increases.

This model allows the stretching frequencies to be examined. Those of interest are the C=C and the C-Cl, which are tabulated below.

Bond	Stretching Frequency (cm-1)
C=C endo	1760.91
C=C exo	1740.75
C-Cl	772.634

Comparison

If I were to compare the results obtained from the different methods I would be lead to conclude that there was a repulsive interaction between the exo double bond and the C-Cl orbital. However this does not make sense and the reason for the increasing distance is just that the three models use many different assumptions. When comparing within the same method a cancellation of errors occurs but the models cannot be reliably compared to each other in a quantitative way.

Hydrogenation

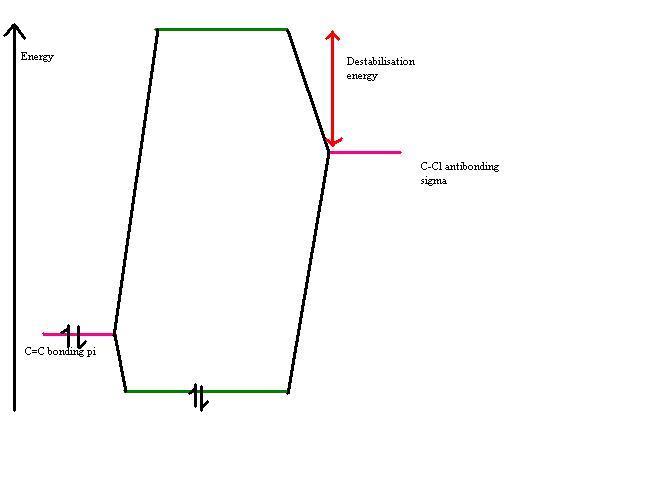
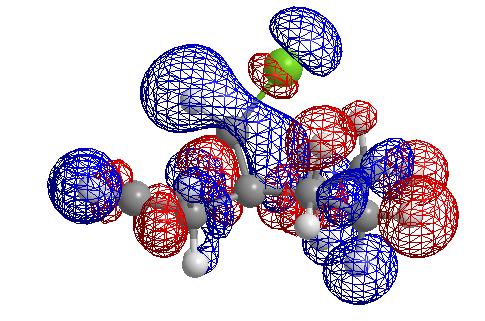
In this molecule, the origin of the selectivity is suspected to come from a donation of electrons from the pi bonding orbital of the exo double bond to the antibonding sigma orbital of the C-Cl bond. If this were the case then upon hydrogenation of the double bond I would expect bothe the C=C and the C-Cl stretching frequencies to be increased (in wavenumbers) as both bonds would get stronger. I would also expect the energy of the LUMO +2 to be lowered as the interaction is removed. The two orbitals interact as shown in the diagram below, hence removing the interaction results in the orbitals having the relative energies shown in pink, wheras in the interacting case they have the relative energies shown in green.(Note that these would be mixed MO's not simple pi or sigma bonds as depicted).

Effect of exo monohydrogenation

The exo hydrogenated product was modelled and it's energy found to be 23.5819 kcal/mol. Upon hydrogenation of the double bond the energy of the LUMO + 2 is reduced due to removal of the interaction between the C=C pi and the C-Cl antibonding orbital. The C-Cl stretching frequency also increases due to a strengthening of the C-Cl bond.

Exo Lumo + 2 orbital

Bond	Stretching Frequency (cm-1)
C=C endo	1757.34
C-Cl	782.313

One would expect upon hydrogenation of the double bond for the energy of the LUMO + 2 to be reduced. This however is not observed, and instead a slight increase in energy is seen. The ernergy of the LUMO+2 is 25.755 eV compared to 24.644 eV in the dialkene. However the total energy of the dialkene is much lower than the exohydrogenated molecule so this could account for the unobserved lowering of the energy levels. Also as the orbitals ar not simple bonding orbitals but comprised of many mixes AO's, the change in the molecule's structure and composition could also account for this.

Vibration of C-Cl bond

Vibration

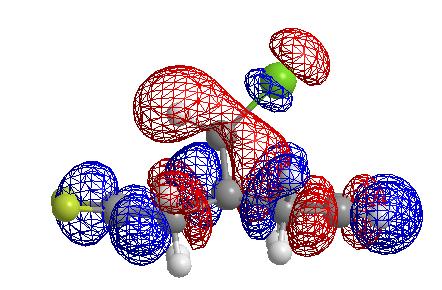
Effect of endo monohydrogenation

As the interaction occurs with the exo pi orbital, one would expect the stretching frequencies in the endo monohydrogenated molecule to be similar to the dialkene. The endo hydrogenated molecule was modelled and its optimised energy found to be 24.7927 kcal/mol. However this is not the case and hydrogenating the endo double bond actually weakens the C-Cl bond and the exo C=C bond relative to the dialkene and reduces it's stretching frequency. The energy of the LUMO + 2 also increases significantly relative to the dialkene suggesting that a larger interaction occurs between the exo alkene and the C-Cl sigma orbital when the endo alkene is hydrogenated. This is as hydrogenation of the endo double bond removes the planarity of the molecule on this side. Hence due to steric repulsion from the hydrogens on the formerly doubly bonded carbons, the lowest energy conformation is one in which the bridgehead carbon lies closer to the exo double bond. The distance is 2.634 amstrong which is significantly shorter than that reported for the dialkene. Hence overlap (and thesrefore overlap integral) of the C=C and C-Cl orbitals is larger and hence interaction is larger (according to the Klopman-Salem expression).

Klopman-Salem expression

Endo LUMO + 2 orbital

Bond	Streching frequency (cm-1)
C=C exo	1740.54
C-Cl	757.685

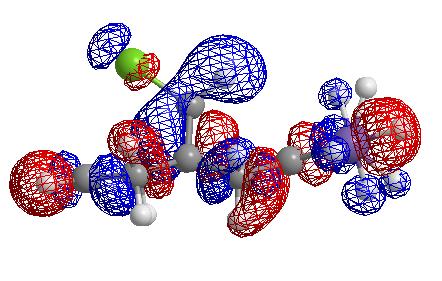
Effect of adding an electron withdrawing group to the exo double bond

To further test the hypothesis that the exo double bond's filled pi orbital donates into the antibonding C-Cl orbital, a model was made in which the two H's on the exo double bond were replaced with fluorine (inductively electron withdrawing). This should result in strengthening of the C-Cl bond and a reduction in the LUMO + 2 energy as the pi bond is less electron rich and hence cannot donate as much electron density into the antibonding orbital. The energy of the LUMO + 2 in this molecule is 24.004 eV (0.64 eV lower than the dialkene). This is indeed the case with a stretching frequency observed almost the same as if the double bond had been removed completely. The C=C bond strength has been increased as it is no longer donating electron density and is thus strengthened despite the inductive elctron withdrawal by the F atoms.

Lumo + 2 orbital

Bond	Stretching frequency (cm-1)
C=C	1761.73
C-Cl	782.315

Effect of adding an electron donating group to the double bond

SiH3 substituents were added (electron donating groups. The C=C bond strength was weakened, and the C-Cl bond was weakened further backing up the suspicion that the pi bond donates into the sigma antibonding orbital. The energy of the LUMO + 2 is 25.360 eV (i.e. increased) corresponding to an increase in the interaction between the two orbitals.

LUMO + 2 orbital

Bond	Streching frequency
C=C	1758.45
C-Cl	770.165

Conclusion

In light of the above evidence, it can be concluded that there is some interaction between the exo double bond and the C-Cl antibonding orbital. However a quantitative analysis cannot be provided and this may not be the sole origin of the increased reactivity of the endo double bond. A more accurate picture of the relative reactivities could be built up by modelling the transition state. The difference between the two relative energies or the transition states (delta delta G) can be substituted inte the following equation; ΔΔG=-RT ln [k/k’] in order to determine the relative rates at which the two bonds react, and thus rationalise the dominance of the endo reacted product.

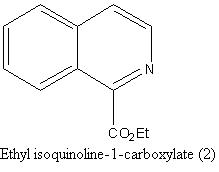
Mini Project - Competitive formation of isoindole and isoquinoline derivatives

Introduction

The synthesis of isoindole derivatives is a relevant topic for investigation as they have attracted much attention for use in organic light emitting diodes due to their high performance as hle transporting materials and their thermal stability. For further information on this topic see Mi et al.’s report.

This project looks at the regio-selectivity of the reaction shown in Scheme 1, as reported by Benjamin Wei-Qiang Hui and Shunsuke Chiba . The major product of the reaction can be changed by changing the reaction conditions, as shown in Scheme 2.

Scheme 1

Scheme 2

Mechanisms and rationalisation of selectivity

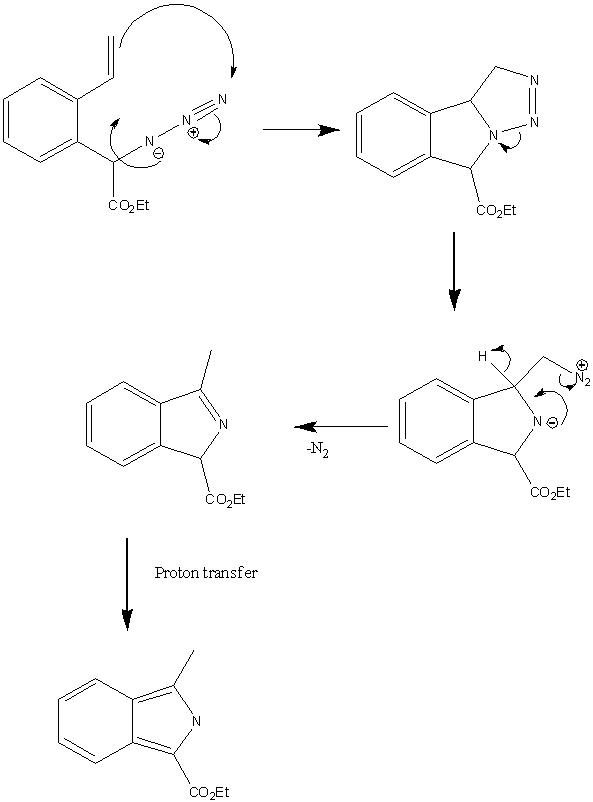
The two products are formed by different mechanisms. The reason for change in selectivity upon addition of base becomes obvious when these are considered. In the absence of base the reaction proceeds via a 1,3- dipolar cycloaddition followed by the elimination of nitrogen to give product 1.

Mechanism for formation of 1

Upon addition of one equivalent of a base such as NaOAc the acidic proton (adjacent to the ester group) is abstracted in and hence the mechanism proceeds via a 6-exo-tet ring closure (Baldwins rules allowed).

Mechanism for formation of 2

Conformation of Products

1 and 2 were modelled in ChemBio3D and their conformations manually optimised and then MM2 optimised. These were then submitted to SCAN for DF optimisation.

1

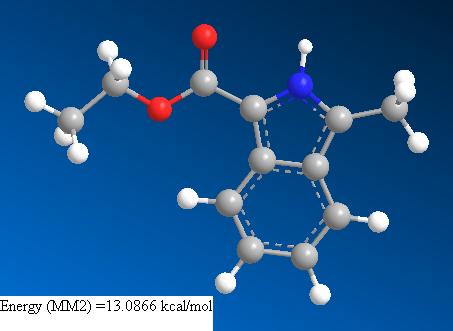
As can be seen in the picture and Jmol, this molecule is rigid and does not have a large number of possible consormations. The aromatic ring system is rigid and planar (Huckels rules). The carbonyl is also planar with respect to the ring to allow overlap of it’s pi cloud with that of the ring to create a conjugated system. The ester group adopts an s-cis conformation. This allows a stabilising anomeric interaction to occur between the antibonding carbonyl sigma orbital and the sp2 oxygen lone pair. It also allows the other oxygen lone pair (in a p-orbital) to be brought into conjugation by overlap with the pi antibonding carbonyl orbital. Hence this molecule is suitable for subjecting to modelling calculations

2

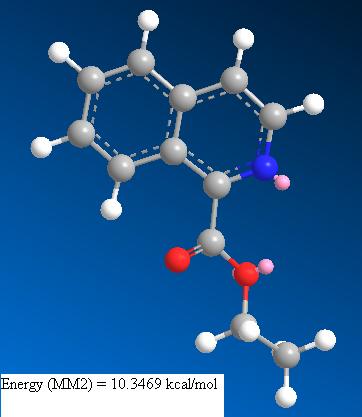
This molecule is also rigid and does not have many possible low energy conformations. As for molecule 1 the aromatic system is rigid and planar and the ester group is held s-cis to allow anomeric stabilisation. As this molecule contains a nitrogen with a lone pair not conjugated into the pi system and a carbonyl group and another oxygen also containing lone pairs, the preferred conformation is one which minimised the steric repulsion between these areas of large electron density whilst allowing some overlap of the carbonyl pi system with that of the ring. Hence the carbonyl is not exactly planar with respect to the ring system.

From the initial MM2 calculation the energy of 2 is lower than that of 1. This explains the experimental observation that when the reaction is done in the absence of base the yield of 1 is 94% as H is a poor leaving group and so will not spontaneously eliminate to allow formation of 2, but in the presence of base, the crucial H can be abstracted as it is acidic and hence the reaction proceeds to give the more stable 2 as the major product.

Both models DF geometry optimisations took 40 minutes (a relatively short amount of time).

NMR

One method of determining which product is obtained from the reaction is analysis of the NMR spectra. These can be predicted using modelling and then compared to those obtained experimentally to identify unknown compounds or verify their identity. Hence NMR spectra were calculated for the two possible products to verify the proposed literature structures were in fact correct and to see how accurate results were obtained from modelling this paticular system.

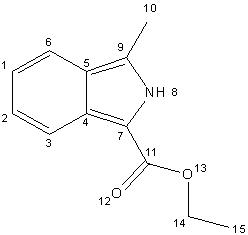
Numbering system used in the assignment of the NMR’s

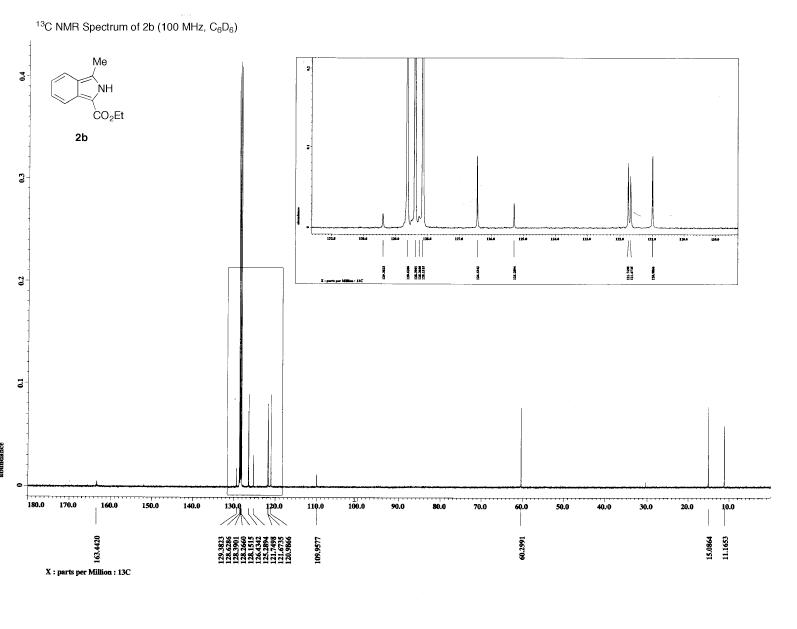
Isoindole 1

Isoquinoline 2

]

The NMR spectra of the two possible products can be used to distinguish between them.

By inspection of the structures of 1 and 2 one would predict that the major difference would be that the 1H NMR of 1 would contain a singlet with an integration ratio of 3H’s at low ppm corresponding to the H’s on carbon 10, which are not part of the aromatic ring and the adjacent carbon ,9, does not have any H’s bonded to it. The 1H NMR of 2 would not contain this peak as all the carbons in 2 are part of the aromatic ring system except the ethyl carbons on the ester substituent (which give triplet and quartet signals).

Similarly in the 13C NMR of 1 one would predict a signal at low ppm corresponding to carbon 10 to appear as this carbon is not deshielded by ring currents as much as those that are part of the aromatic ring are. In 2 this signal would not be present as all the carbons except the (ethyl carbons) are part of the aromatic ring system.

Both the experimentally derived and the calculated NMR spectra show this and hence one may conclude that the authors have correctly identified each product, as the spectra are in accord with those predicted from modelling and also with those expected from inspection of the structures.

Results of NMR calculations of 1

http://hdl.handle.net/10042/to-1649

1H NMR spectra

The calculated 1H spectra of 1 and the experimental spectra from the literature are shown below.

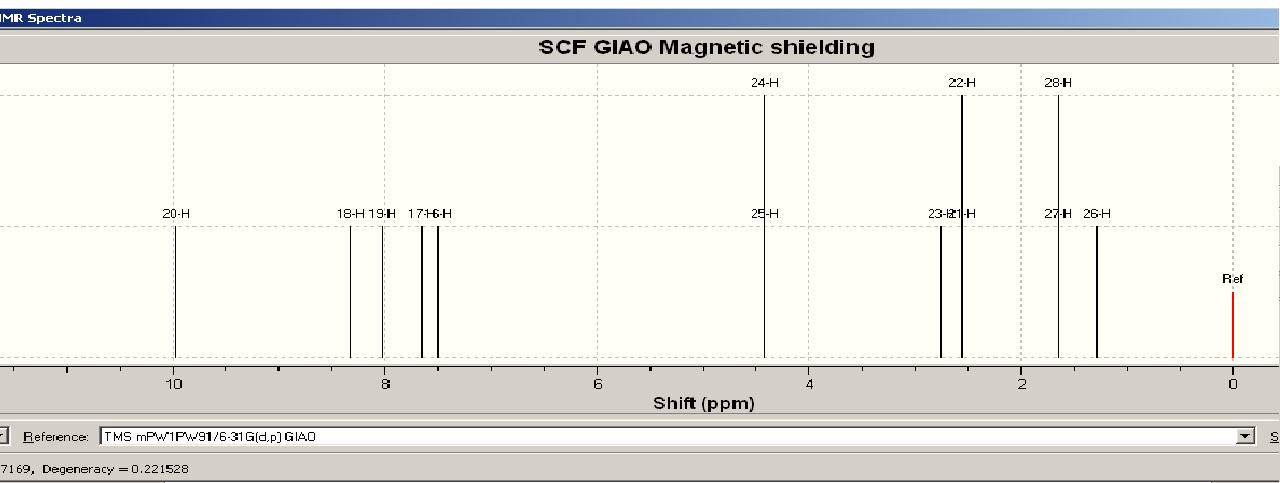
Calculated

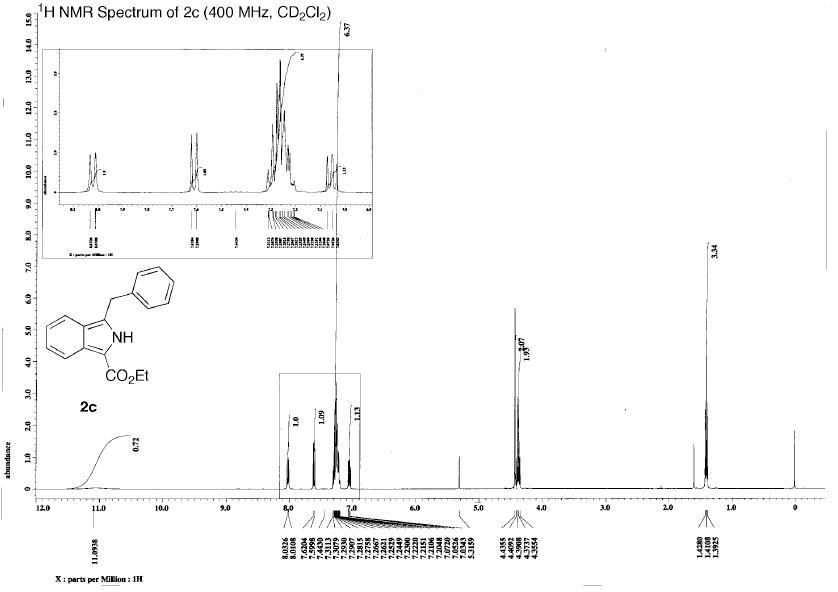
Experimental

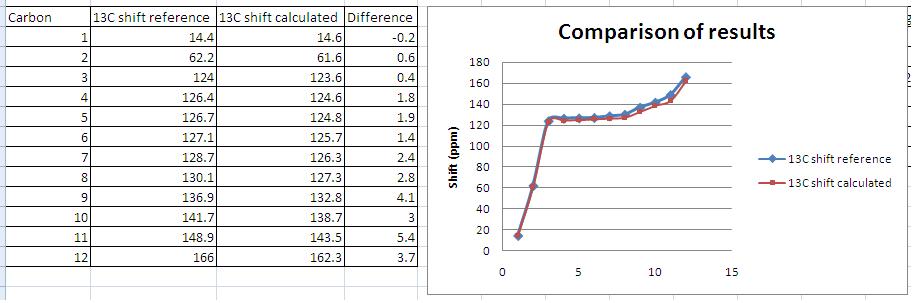
Assigning the peaks (this was not done in the literature, see comparison for my assignment) allows rationalisation of the spectra. The results are as predicted – there is a singlet at low ppm corresponding the the 3H’s on C10 in both the experimental and calculated NMR.

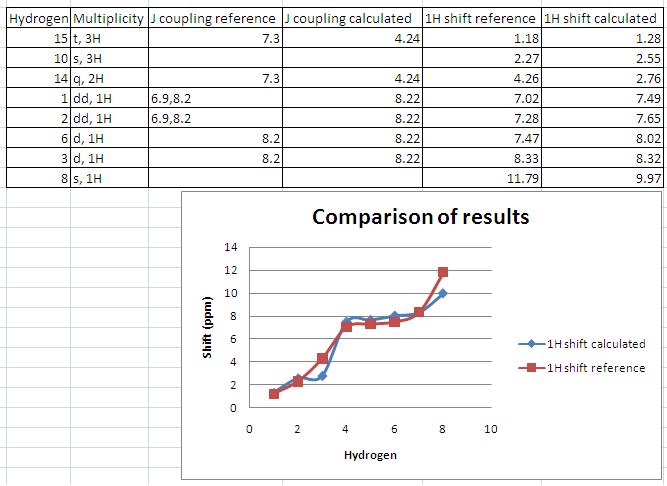
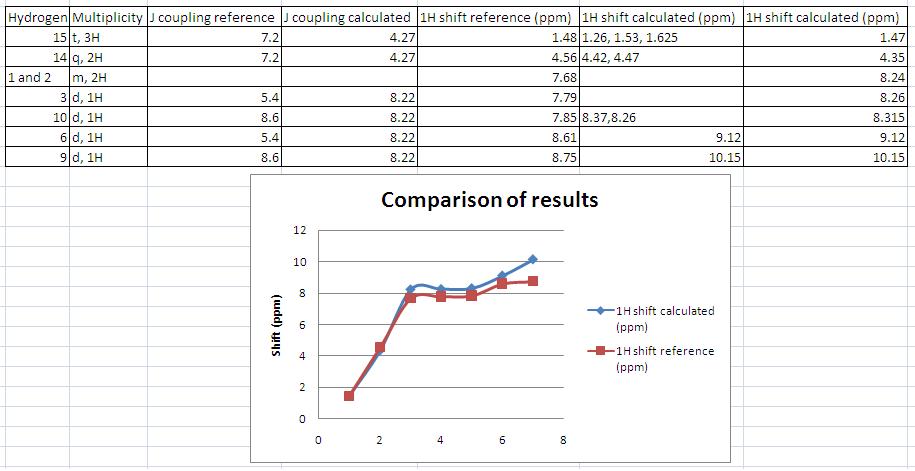
The coupling constants were calculated using jannochio (see below). These were in good accord with the literature for the aromatic protons but not for the ethyl protons. However the double doublet aromatic protons on carbons 1 and 2 were predicted to couple to each other with the same constant as to 3 (or 6). This is not the case in reality and arises as the prediction is based upon the karplus equation which only takes into account the distance and dihedral angle when calculating the coupling constants. In the model all the ring protons are in the plane of the ring and the distance between them is equal hence the prediction is the same.

The NMR obtained from calculations was not exactly the same as that obtained experimentally, although they did show many similarities. One interesting observation is that the modelling seemed least accurate for protons close to heteroatoms (see graph). The deviation from experimentally derived results could be down to a number of factors (which are discussed at the end of this section). In the case of predicting the spectra of hydrogen nuclei, generally more accurate techniques are required to provide useful results so it is expected that the obtained spectra would deviate somewhat from the experimental, but by how much is of particular interest as molecular modelling of NMR to predict spectra is still a relatively new technique. In order to compare the differences and hence gain insight into how accurate the modelling was, and the particular areas in which it fell down, the calculated and experimental shifts were plotted onto a scatter graph. This is shown in the comparison below along with my assignment of the peaks.

Analysis of results

13C spectra

The experimental and calculated 13C spectra of isoindole 1 are shown below.

Calculated

Experimental

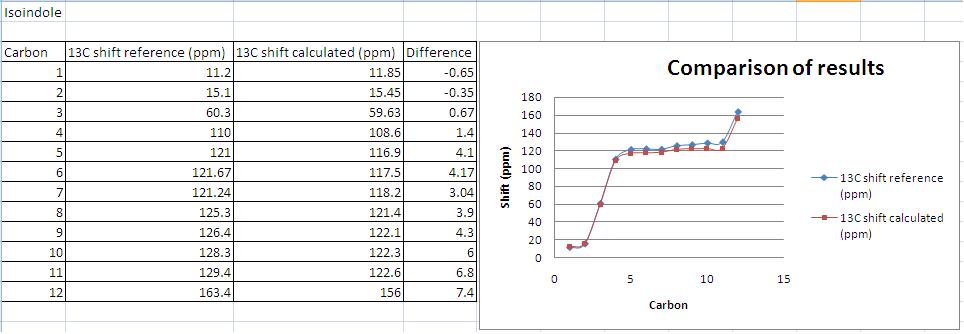
As before the spectra deviates from that obtained experimentally but plotting of the calculated and experimental results shows much better correlation than that observed for 1H NMR predictions, with only 3 shifts deviating by more than 5 ppm. Note that the 13C numbers shown in the graph are not the assignments. The modelling seems most accurate for the lower chemical shifts, with larger deviations occurring for the more deshielded carbons (in particular those adjacent to heteroatoms as was the case in the 1H NMR).

Analysis of results

Results of NMR calculations of 2

http://hdl.handle.net/10042/to-1650

1H NMR spectra

Calculated

As can be seen in the analysed data below, the calculation gives good predicitions for lower shifts with the deviation from experimental results increasing as chemical shift increases. The coupling constants are not predicted so well in this case for the same reasons outlined in prior dicusion. The results for 2 are noticeably better than those for 1, this is probably due to the correct solvent reference (CDCl3) being available in GaussView for 2.

As expected, the singlet with an integration ration of 3H at 2.55 ppm (calculated) or 2.27 ppm (experimental) is not present, indicating no methyl ring substituent is present in 2.

Unfortunatly the literature did not provide the actual NMR spectra of isoquinoline 13, only the written data. (hence why there are no pictures of them for comparison in this section).

The multiplicities of the peaks in the literature are in accord with those expected from the given structure (note that H’s on carbons; 9 and 10 couple; 1 couple to those on 2 and 6 and 2 couple to those on 1 and 3). Hence one can conclude that their proposed structure is correct based on these models.

Analysis of results

13C NMR spectra

Calculated

Again the lowfield signal of carbon 10 dissapeared indicating no methyl substituents. The correlation of the data to that obtained experimentally was again much better than for 1, with only one result deviating by more than 5ppm. The same trend regarding magnitude of shift and accuracy of modelling was observed.

Analysis of results

Some reasons why calculated NMRs deviated from experimentally measured NMR'

The results obtained from NMR calculations were not exactly the same as the experimental spectra obtained. This could be down to a number of factors:

For isoindole 1 the solvent used for both 1H NMR and 13C NMR in the literature is C6D6 (this is not the case for isoquinoline 2 where the solvent is CDCl3). Calculations were run both with benzene and chloroform as the reference solvent. As Gaussian does not have a C6D6 reference option for viewing NMR results both calculations gave the same spectra (see comparison) when TMS alone was chosen as reference for the C6D6 calculation and TMS/CDCL3 was chosen for the other. In order to get an accurate comparison C6D6 reference would need to be chosen in the GaussView package. This is a limitation of the software.

The conformation put into the NMR calculation may be slightly different to that which the molecule adopts in reality, this could be due to the software getting stuck in an energy well when minimising the energy, or due to solvent effects making another conformation more preferable in solution. This may have occurred as MM2 does not take into account electronic/orbital interactions and so the initial geometry put into the DF geometry optimisation my not have been the most favourable. This is particularly true of the molecules at hand as they experience many stereoelectronic secondary interactions such as the anomeric effect. Hence there is scope for both human error and calculation error in finding the lowest energy/most preferred conformation of the molecule.

Experimental NMR is affected by bond rotation. Fast rotation on the NMR timescale may result in protons which are seen as inequivalent in the stationary model put into the DF calculations appearing equivalent experimentally. Broad signals are often due to exchange and NMR experiment having a similar timescale. An example of this can be seen in the 1H spectra of 1. The experimental NMR shows a broad singlet at 1.18 ppm with an integration ratio of 3, corresponding to the H’s on carbon 15 wheras the DF calculation returns a peak at 1.28 ppm with an integration ration of 1 and a peak at 1.66 ppm with an integration ratio of 2 for the H’s on carbon 15.

The resolution of the NMR machine also limits the experimental results. If the separation of peaks is smaller than the resolution then they will appear as overlapping peaks or multiplets that can be hard to assign. This does not happen with calculated NMR spectra so whereas the literature may quote a multiplet over a range of ppm with a large integration ratio, the calculated NMR will give each individual peak.

Deviations could also be down to approximations in the DF method or the choice of basis set or density functional. Without very detailed mathematical understanding of all the different basis sets and density functionals it is hard to predict which is the best to use. For an excellent and understandable overview of density functional methods I recommend Computational Chemistry: A Practical Guide for Applying Techniques to Real-World Problems, by David C. Young (see references).

As GaussView only provides NMR reference data for a few basis set/density functional combinations the number of possibilities is limited. This is a limitation of the DF method and GaussView package.

IR Spectra

The IR spectra were also calculated and assigned for 1 and 2 (note the literature did not provide IR data for 2 so it was taken from an alternative source)

The IR spectra of 1 and 2 could also be used to differentiate between them. One would expect 1 to show an absorbance at around 3400 cm-1 corresponding to the N-H stretch and around 1500-1650cm-1 corresponding to the bend. 2 does not have an N-H bond and so one would not expect to see these absorbencies in its spectra.

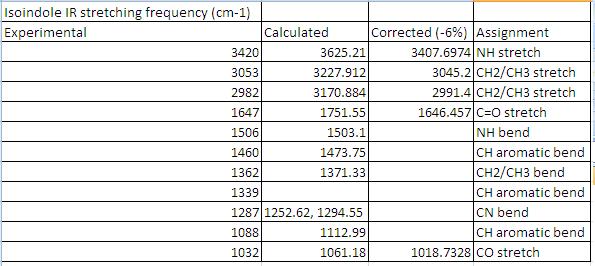
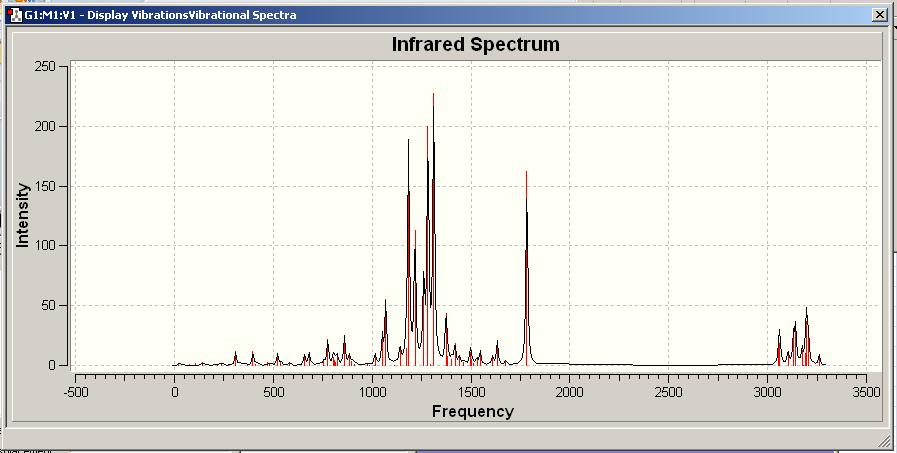
IR Spectra of 1

Comparison to literature

As expected there is an NH stretching and bending absorbance seen in both the experimental and calculated IR spectra. The calculated IR spectra was in good accord to that obtained experimentally once an empirical correction of -6% had been applied to each of the stretching frequencies. (The model is known to overestimate these).

IR Spectra of 2

Comparison to literature

As predicted there is no NH stretch or bend in either the literature or calculated spectra indicating that there is no NH bond in 2 and hence providing wevidence that it has the suggested structure. The calculated data was again in good accord once the empirical corrections had been applied.

Summary

Molecular modelling has successfully been used to model the conformations, energies, IR spectra, 1H NMR and 13C NMR spectra of 1 and 2. The results have been found to correlate well but not perfectly to the experimentally derived data. The characterisation of the two possible products, 1 and 2, in the literature has been confirmed as correct. Some limitations of the modelling technique and sources of error have been highlighted and discussed.

Conclusions

Molecular modelling has proved itself reasonably accurate in this particular example. The results do not correlate perfectly but do so well enough to be useful. However I feel that with increased use (to improve knowledge of basis sets, density functionals and geometry optimisation) even better results could be obtained in future and thus molecular modelling has great potential in aiding chemists characterise unknown compounds and rationalise selectivity of reactions.