Rep:Mod:fkl11phymod18
Y3C Experiment: Physical Module
Name: Fong Kai Lee
CID number: 00690790
The Cope Rearrangement
Introduction
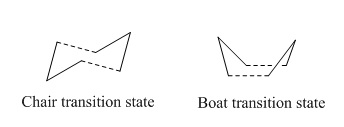
Cope rearrangement involves a symmetry-allowed [3,3]-sigmatropic shift or π2 + σ2 + π2 cycloaddition in a 1,5-diene molecule. [1] Experimental and theoretical studies have been done in determining the preferred mechanism and transition state of the Cope reaction as the mechanism was the topic of some controversies. The possible mechanisms of Cope rearrangement include concerted, stepwise or dissociative mechanism whereas a 'chair' or 'boat' transition structure are two possible transition states of this reaction. [2] Cope rearrangement of 1,5-hexadiene is studied in this experiment in terms of its low-energy minima and transition structures on its potential energy surface, in an attempt to determine the preferred reaction mechanism.
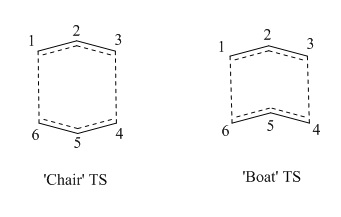
The figure below shows the Cope rearrangement of 1,5-hexadiene and possible transition states in the reaction:

Optimisation of Reactants and Products
Point Group and Energy of Conformers
Two anti and one gauche 1,5-hexadiene conformers were generated in GaussView before being optimised by Gaussian software.
The table below shows the structure (with labelled atoms) of three simulated conformers with their point groups included:
| Conformer of 1,5-hexadiene | Structure | Point group |
| anti |  
|
C2h |
| anti |  
|
Ci |
| gauche |  
|
C2 |
Note that Newman projection of each conformer is shown as the second figure in the 'Structure' column. From the Newman projections above, the two terminal enyl groups in anti conformers are antiperiplanar to each other.
The calculations for the optimisation of the conformers (with stated point groups) can be found from the links stated below:
HF method with 3-21G basis set:
anti 1,5-hexadiene (C2h): DOI:10042/28008
anti 1,5-hexadiene (Ci): DOI:10042/28009
gauche 1,5-hexadiene (C2): DOI:10042/28014
B3LYP method with 6-31G(d) basis set:
anti 1,5-hexadiene (C2h): DOI:10042/28011
anti 1,5-hexadiene (Ci): DOI:10042/28012
gauche 1,5-hexadiene (C2): DOI:10042/28015
The table below shows the minimum energies calculated for optimised conformers (with stated point groups) using two different methods and basis sets. The energy difference between the conformers based on the two methods and basis set are also shown in the table below:
| Conformer of 1,5-hexadiene | Method and energy / a.u. | Relative energy difference / a.u. | ||
| HF/3-21G | B3LYP/6-31G(d) | HF/3-21G | B3LYP/6-31G(d) | |
| anti (C2h) | -231.68907067 | -234.60964388 | 0.0034646 | 0.0020665 |
| anti (Ci) | -231.69253528 | -234.61171035 | 0.0000000 | 0.0000000 |
| gauche (C2) | -231.69166701 | -234.61068493 | 0.0008682 | 0.0010254 |
From the table above, it is clear that anti 1,5-hexadiene with point group of Ci has the lowest energy among all three conformers using two different methods and basis set. The energies of conformers obtained using B3LYP/6-31G(d) are compared with theoretical value obtained from literature. From literature, the absolute energy of 1,5-hexadiene was found to be -234.61171 hartree or -234.61171 a.u.. Note that the absolute energy of the molecule obtained from literature was calculated based on Becke3LYP/6-31G* level, which is essentially same as B3LYP/6-31G(d) level used in this experiment.[3] Based on the comparison, anti 1,5-hexadiene (Ci) has almost identical absolute energy (-234.61171035 a.u.) as the literature value with accuracy up to 5 decimal places. This may indicate that the structure simulated in the literature source is anti 1,5-hexadiene (Ci) which is the most thermodynamically stable among the three conformers even though the conformation of 1,5-hexadiene had not been stated explicitly in the literature source.
It is worth to compare the energies between anti (Ci) and gauche (C2) conformers which have different conformations. Gauche (C2) conformer is less thermodynamically stable than anti (Ci) conformer which maybe due to the steric repulsion between the two enyl groups that are relatively close in distance to each other than in anti conformation.
Geometries of Conformers
The bond lengths and bond angles for all three conformers based on two different methods and basis set are shown in the table below:
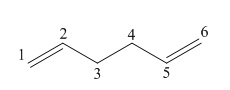
| Conformers and Methods | Bond length / Å | Bond angle / ° | ||||
| C1-C2 / C5-C6 | C2-C3 / C4-C5 | C3-C4 | C1-C2-C3 / C4-C5-C6 | C2-C3-C4 / C3-C4-C5 | ||
| anti (C2h) | HF/3-21G | 1.317 | 1.514 | 1.535 | 127.1 | 114.8 |
| B3LYP/6-31G(d) | 1.334 | 1.508 | 1.529 | 127.3 | 115.7 | |
| anti (Ci) | HF/3-21G | 1.316 | 1.509 | 1.553 | 124.8 | 111.4 |
| B3LYP/6-31G(d) | 1.334 | 1.504 | 1.548 | 125.3 | 112.7 | |
| gauche (C2) | HF/3-21G | 1.316 | 1.509 | 1.551 | 125.0 | 112.0 |
| B3LYP/6-31G(d) | 1.333 | 1.504 | 1.548 | 125.4 | 113.6 | |
From literature, 1,5-hexadiene has following bond lengths and bond angles. Note that the data was obtained from electron diffraction studies of the molecule: [4]
C1-C2: (1.340 ± 0.003) Å
C2-C3: (1.508 ± 0.012) Å
C3-C4: (1.538 ± 0.027) Å
C1-C2-C3: (124.6 ± 1.0)°
C2-C3-C4: (111.5 ± 0.9)°
In general, the calculated bond angles of three conformers at two levels of theory are almost identical but there are slight differences in their calculated bond lengths. The bond lengths of conformers calculated at B3LYP/6-31G(d) level are closer to the literature values especially for C1-C2 and C3-C4 bond lengths than at HF/3-21G level. This may be due to the reason that B3LYP/6-31G(d) is a higher level of theory set which takes more approximations into account in estimating the geometries of the conformers than HF/3-21G does.
Vibrational Frequencies and Thermochemistry of anti 1,5-hexadiene (Ci)
Vibrational frequencies of anti 1,5-hexadiene (Ci) has been calculated based on previous optimised molecule where optimisation of molecule was carried out using B3LYP method with 6-31G(d) basis set. The calculations for the vibrational frequenices and thermochemistry data of the molecule can be found from the following link: DOI:10042/28016
Two lines of low frequencies from the log file (which can be found from link above) are presented below:
Low frequencies --- -9.4844 -0.0009 -0.0005 0.0005 3.7505 13.0164 Low frequencies --- 74.2861 80.9996 121.4176
The first line of 'low frequencies' values are within ± 15 cm-1 and absence of negative frequencies observed in the second line of 'low frequencies' values indicate that the molecule is fully optimised.
The figure below shows the predicted IR spectrum of anti 1,5-hexadiene (Ci):

The table below shows the calculated thermochemistry data of anti 1,5-hexadiene (Ci):
| Thermochemistry data | ||||
| Sum of electronic and zero-point energies (at 0 K) / a.u. | Sum of electronic and thermal energies (at 298.15 K and 1 atm of pressure) / a.u. | Sum of electronic and thermal enthalpies / a.u. | Sum of electronic and thermal free energies / a.u. | |
| anti 1,5-hexadiene (Ci) | -234.469204 | -234.461857 | -234.460913 | -234.500777 |
Optimisation of the 'Chair' and 'Boat' Transition Structures
HF/3-21G Level
An allyl fragment of CH2CHCH2 molecule was created in GaussView and optimised by Gaussian using HF/3-21G level. The calculations of optimisation of CH2CHCH2 can be found from following link: DOI:10042/28017
By combining two optimised allyl fragments with correct orientation, 'chair' and 'boat' transition strictures are created in GaussView respectively. For the 'chair' transition state, it was optimised and its frequencies were calculated at the same time using HF/3-21G level. Additional keyword 'Opt=NoEigen' which can stop the calculation crashing if more than one imaginary frequency is detected during the optimisation was added. This incident can occur if the guess transition structure is not good enough. The described method in this context will be referred as 'normal' method. The 'chair' transition state was optimised again using the frozen coordinate method but at the same level. As the name suggests, frozen coordinate method involves 'freezing' of reaction coordinate (bonds formed or broken) and optimising the rest of the molecule. This is followed by 'unfreezing' of the reaction coordinate and the transition state optimization is started again.
The 'boat' transition state was optimised using QST2 method but at the same HF/3-21G level. This method involves the proposed transition state based on interpolation between the created reactant and product molecules.
The calculations for the optimisation of both transition states can be found in the following links:
'Chair' transition state ('normal' method): DOI:10042/28027
'Chair' transition state (frozen coordinate method): DOI:10042/28028
'Boat' transition state (QST2 method): DOI:10042/28029
The table below shows the energies and imaginary frequencies obtained for optimised 'chair' and 'boat' transition structures:
| Method | 'Chair' transition state | 'Boat' transition state | ||
| Energy / a.u. | Imaginary frequency / cm-1 | Energy / a.u. | Imaginary frequency / cm-1 | |
| 'Normal' | -231.61932238 | -817.93 | n/a | n/a |
| Frozen coordinate | -231.61932230 | -817.87 | n/a | n/a |
| QST2 | n/a | n/a | -231.60280222 | -840.23 |
The energies obtained for 'chair' transition state using two different methods are almost identical (up to six decimal places) which means that both methods employed are capable in optimising the transition states. The 'chair' transition state is more thermodynamically stable than 'boat' transition state. This is because pseudo eclipsed conformations can be observed in the 'boat' transition state where there are steric repulsions between the groups of atoms at the terminals of allyl fragment of CH2CHCH2 molecules.
The figures below show the motions of both 'chair' and 'boat' transition states corresponding to their imaginary frequencies based on each method:
Negative or imaginary frequencies obtained from optimisation of transition states using three different methods indicate the structures optimised are indeed the transition states. For 'chair' transition state, the motions that correspond to obtained imaginary frequencies are almost identical despite there is very slight difference in the imaginary frequencies values.
Intrinsic Reaction Coordinate
Intrinsic Reaction Coordinate (IRC) is used to follow the minimum energy pathway from 'chair' or 'boat' transition structure down to its local minimum on a potential energy surface. This allows us to deduce which conformer is formed from the transition structure. IRC takes a series of points by taking a very small geometry changes in the direction where the gradient or slope of the energy surface is steepest. The number of points it takes is defined by N and it can be modified. In this case, N = 50 and N = 100 are taken for both transition structures. IRC is calculated based on transition structures that are optimised by HF/3-21G level.
The calculations of IRC for the transition states are found from the links below:
For N = 50:
'Chair' transition state ('notmal'): DOI:10042/28030
'Boat' transition state (QST2): DOI:10042/28032
For N = 100:
'Chair' transition state ('notmal'): DOI:10042/28031
'Boat' transition state (QST2): DOI:10042/28033
The figures below shows the IRC graph and its motion path to formation of product for 'chair' and 'boat' transition structures:
| 'Chair' transition state | 'Boat' transition state | |||
| Graph | Animation | Graph | Animation | |
| N = 50 | 
|

|

|
|
| N = 100 | 
|
|

|

|
IRC calculations reveal that the optimised transition states do indeed lead to the formation of same product via lowest energy pathways. In each case, once the product is formed, the C-C bonds rotate in order for the product to adopt the conformation which has the lowest energy. This observation is more obvious in the case of 'boat' transition state where the central vertical C-C bond rotates in order to avoid eclipsed conformation that is initially adopted by the product.
B3LYP/6-31G(d) Level
Previous optimised transition structures were optimised at higher B3LYP/6-31G(d) level.
The calculations for optimisation of 'chair' and 'boat' transition states can be found from the links below:
For 'chair' transition state ('normal'): DOI:10042/28036
For 'boat' transition state (QST2): DOI:10042/28034 (optimisation) and DOI:10042/28035 (frequency calculations)
The table below shows the energies and imaginary frequencies (with animations) obtained for optimised 'chair' and 'boat' transition structures:
| 'Chair' transition state | 'Boat' transition state | |
| Energy / a.u. | -234.55698303 | -234.54309297 |
| Imaginary frequency / cm-1 | -565.54 | -530.54 |
| Front view | 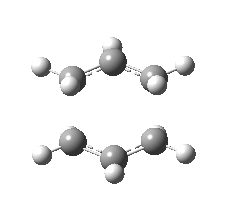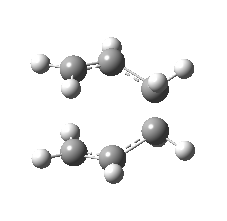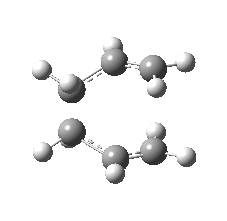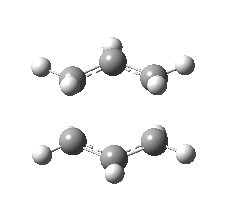
|
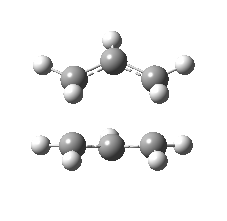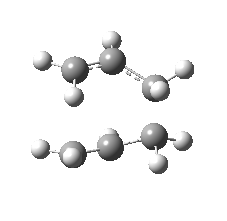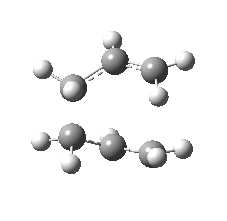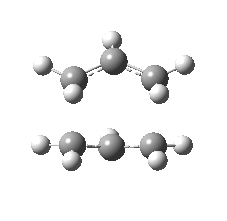
|
| Side view | 
|
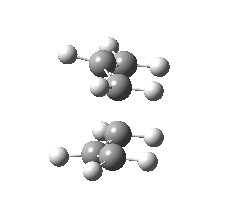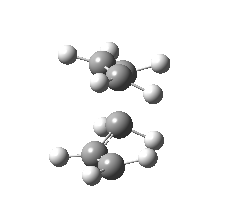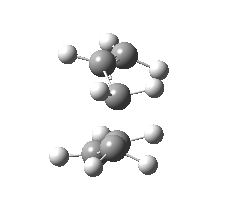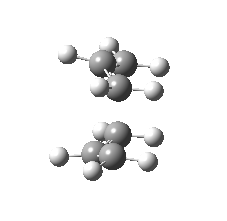
|
Geometries and Energies of Transition Structures
The table below shows the geometries of transition structures that are calculated using HF/3-21G and B3LYP/6-31G(d) levels:
| HF/3-21G | ||||||
| Bond length / Å or angle / ° | 'Chair' transition state | 'Boat' transition state | ||||
| 'Normal' | Frozen coordinate | QST2 | ||||
| C1-C6 / C3-C4 (through space) | 2.020-2.021 | 2.021 | 2.140 | |||
| C1-C2 / C2-C3 / C4-C5 / C5-C6 | 1.389 | 1.389 | 1.382 | |||
| C1-C2-C3 / C4-C5-C6 | 120.5 | 120.5 | 121.7 | |||
| B3LYP/6-31G(d) | ||||||
| C1-C6 / C3-C4 (through space) | 1.968 | n/a | 2.206-2.207 | |||
| C1-C2 / C2-C3 / C4-C5 / C5-C6 | 1.407-1.408 | n/a | 1.393 | |||
| C1-C2-C3 / C4-C5-C6 | 120.0 | n/a | 122.3 | |||
The table below shows the energies obtained for transition states that are calculated using HF/3-21G and B3LYP/6-31G(d) levels:
| Method | 'Chair' transition state | 'Boat' transition state | ||
| Energy (HF/3-21G level) / a.u. | Energy (B3LYP/6-31G(d) level) / a.u. | Energy (HF/3-21G level) / a.u. | Energy (B3LYP/6-31G(d) level) / a.u. | |
| 'Normal' | -231.61932238 | -234.55698303 | n/a | n/a |
| Frozen coordinate | -231.61932230 | n/a | n/a | n/a |
| QST2 | n/a | n/a | -231.60280222 | -234.54309297 |
The geometries obtained for 'chair' and 'boat' transition states at two levels are reasonably similar but the energy differences are significantly large. B3LYP/6-31G(d) is a higher level of theory set which takes more approximations into account in estimating the geometries of the transition states than HF/3-21G does. As discussed in previous section, the 'chair' transition state is more thermodynamically stable than 'boat' transition state regardless of the level of theory employed in calculations. This is because pseudo eclipsed conformations can be observed in the 'boat' transition state where there are steric repulsions between the groups of atoms at the terminals of allyl fragment of CH2CHCH2 molecules.
The table below shows the thermochemistry data of transition states and reactant (anti 1,5-hexadiene (Ci)) which are optimised using B3LYP/6-31G(d) level:
| Thermochemistry data | |||||
| Electronic energy / a.u. | Sum of electronic and zero-point energies (at 0 K) / a.u. | Sum of electronic and thermal energies (at 298.15 K and 1 atm of pressure) / a.u. | Sum of electronic and thermal enthalpies / a.u. | Sum of electronic and thermal free energies / a.u. | |
| 'Chair' transition state ('normal') | -234.55698303 | -234.414929 | -234.409009 | -234.408065 | -234.443814 |
| 'Boat' transition state (QST2) | -234.54309297 | -234.402340 | -234.396006 | -234.395061 | -234.431751 |
| Reactant (anti 1,5-hexadiene (Ci)) | -234.61171035 | -234.469204 | -234.461857 | -234.460913 | -234.500777 |
The figure below shows the progress of a generic reaction against its energy of the system:
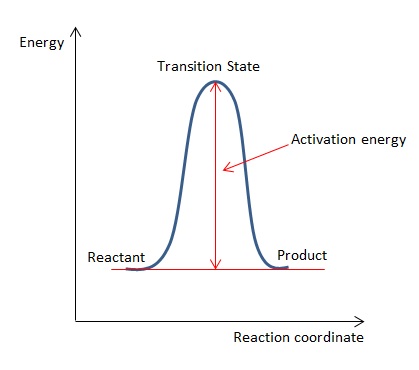
The reactant and product have the same energies as indicated in the energy profile diagram above as they are essentially the same molecule (1,5-hexadiene). The activation energy of the reaction via 'chair' or 'boat' transition state at 0 K is calculated by subtracting the sum of electronic and zero-point energies (at 0 K) for transition state from that of reactant. Hence, the activation energy of reaction via 'chair' transition state is 0.054275 a.u. (or 34.1 kcal mol-1) and via 'boat' transition state is 0.066864 a.u. (or 42.0 kcal mol-1). These results are compared with literature values where the activation energy of the reaction via 'chair' transition state is (33.5 ± 0.5) kcal mol-1 [5] and (44.7 ± 2.0) kcal mol-1 via 'boat' transition state. [6] The calculated result for 'chair' transition state agrees well with the literature value but there is larger difference in calculated result for 'boat' transition state with literature value. In theory, 1,5-hexadiene would undergo Cope rearrangement via 'chair' transition state due to smaller activation energy barrier than it would in 'boat' transition state.
The Diels-Alder Cycloaddition
Introduction
The Diels-Alder reaction is a well known pericyclic reaction which is very useful in synthetic organic chemistry. The reaction involves overlap of π orbitals of the dieneophile (in this case ethylene) with π orbitals of the diene (in this case cis butadiene) which leads to formation of new σ bonds. The number of π electrons involved in the reactions determines whether the reaction proceeds via synchronous concerted fashion (allowed) or not (forbidden). In Zimmerman's model, if the number of electrons in a Möbius or Hückel system is 4n or 4n+2 respectively, then the reaction is classified as allowed. K. Fukui assumed that a chemical reaction can proceed at the position where HOMO and LUMO of the reacting species overlap the most and this is important in pericyclic reactions. The overlap parameter or density of HOMO and LUMO orbitals depend strongly on their symmetry properties. The HOMO and LUMO orbitals can interact with each other when they have same symmetry properties (as shown by the sketched orbitals in figure below) which leads to high overlap density. [7]
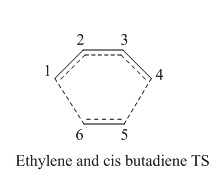
The figures below show the Diels-Alder cycloaddition reaction between cis butadiene and ethylene:

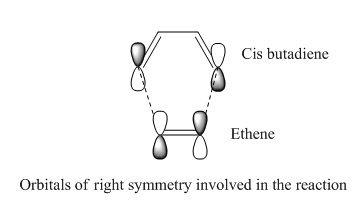
In this exercise, the transition structure of reaction between cis butadiene and ethylene is investigated with considerations of the symmetries of HOMO/LUMO of butadiene and transition state being taken into account.
Optimisation of Cis Butadiene
A molecule of cis butadiene was created in GaussView and optimised by Gaussian. The methods used in optimisation of cis butadiene were semi-empirical/AM1, HF/3-21G followed by B3LYP/6-31G(d) which was the highest level deployed in this optimisation. The calculations for optimisation of the molecules using different methods can be found from the links below:
Semi-empirical/AM1: DOI:10042/28041
HF/3-21G: DOI:10042/28042
B3LYP/6-31G(d): DOI:10042/28043
The table below shows the calculated energies for cis butadiene based on three different methods:
| Method | |||
| Semi-empirical/AM1 | HF/3-21G | B3LYP/6-31G(d) | |
| Energy / a.u. | 0.04879719 | -154.05394305 | -155.98594961 |
HOMO/LUMO of Cis Butadiene
Prediction of molecular orbitals (MOs) of cis butadiene was carried out based on optimised molecule using B3LYP/6-31G(d) level. The calculations of the HOMO/LUMO of the molecule can be found from the following link: DOI:10042/28044
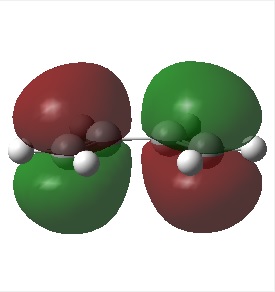
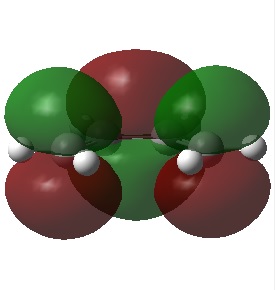
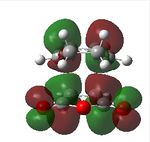
The figures below show the HOMO and LUMO of cis-butadiene (from front view) and its symmetry with respect to the plane of symmetry:
| HOMO of cis butadiene (anti-symmetric) | LUMO of cis butadiene (symmetric) |
|
|
Based on figures above, the LUMO of cis butadiene is determined to be symmetric with respect to the reflection plane and its HOMO is antisymmetric.
Optimisation of Ethylene and Cis Butadiene Transition Structure
Ethylene and cis butadiene transition state was created in GaussView and optimised by Gaussian using semi-empirical/AM1, HF/3-21G and B3LYP/6-31G(d) levels. Frozen coordinate method was used in optimisation of the transition state. The calculations for the optimisation and frequency calculations of the transition state based on three different methods can be found from the links below:
Semi-empirical/AM1: DOI:10042/28061
HF/3-21G: DOI:10042/28062
B3LYP/6-31G(d): DOI:10042/28063
The table below shows the energies and imaginary frequencies obtained for the transition state based on different methods:
| Semi-empirical/AM1 | HF/3-21G | B3LYP/6-31G(d) | |
| Energy / a.u. | 0.11165475 | -231.60320841 | -234.54389650 |
| Imaginary frequency / cm-1 | -956.20 | -818.23 | -524.94 |
| Front view | 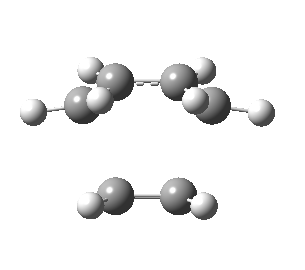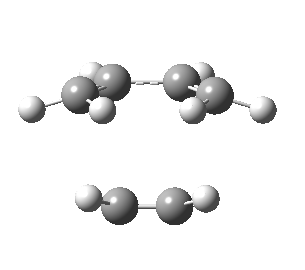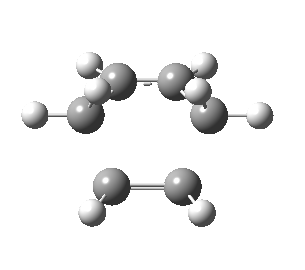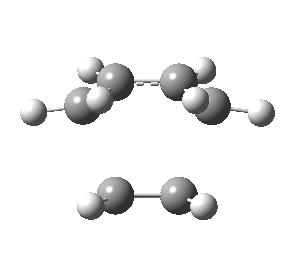
|
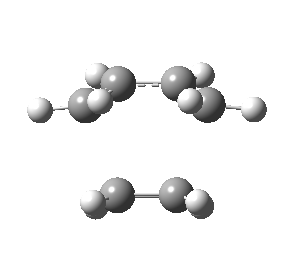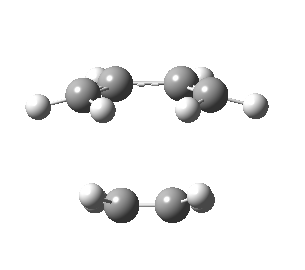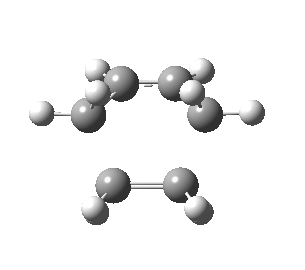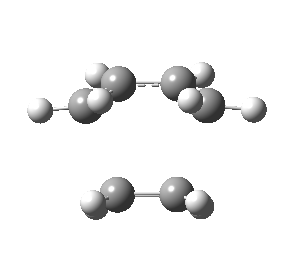
|

|
| Side view | 
|
|

|
The figures below show the calculated imaginary and least negative frequencies of the transition state that was optimised at HF/3-21G level:
| HF/3-21G | ||
| Imaginary frequency / cm-1 | -818.23 | 166.68 |
| Front view | 
|
|
| Side view | 
|
|
Negative frequency obtained for the transition state at each level indicates that the optimised structure is indeed the transition structure. The motion of transition state that corresponds to the imaginary frequency is synchronous while the rocking motion corresponds to the least negative frequency is asynchronous.
HOMO/LUMO of the Transition Structure
Prediction of molecular orbitals (MOs) of the ethylene and cis butadiene transition structure was carried out based on optimised molecule using HF/3-21G level. The calculations of the HOMO/LUMO of the transition state can be found from the following link: DOI:10042/28064
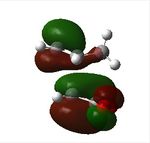
The figures below show the HOMO and LUMO of ethylene and cis butadiene transition state and its symmetry with respect to the plane of molecule:
| HOMO-1 of transition state (anti symmetrical) | HOMO of transition state (anti symmetrical) | LUMO of transition state (symmetrical) | |
| Energy level / a.u. | -0.30291 | -0.30086 | 0.14236 |
| Front view | 
|

|

|
| Side view | 
|

|

|
The HOMO of the transition state is determined to be anti symmetrical and LUMO to be symmetrical. There is a possibility that HOMO-1 and HOMO are degenerate orbitals since their energy levels are fairly close to each other. In the HOMO of transition state, it seems that there is a nodal plane between the cis butadiene and ethylene fragments whereas in HOMO-1 orbital, no nodal plane between the two fragments but a nodal plane perpendicular to plane to the transition state is observed. This could explain their possible degeneracy since there is a major nodal plane in each orbital. Assume that the two orbitals are degenerate, from inspection, the HOMO of cis butadine interact with LUMO of ethylene to form anti symmetrical HOMO-1 of transition state since the orbitals on cis butadiene fragment resembles the HOMO of cis butadiene.
Geometry of the Transition Structure
The table below shows the geometry of ethylene and cis butadiene transition structure that was calculated at semi-empirical/AM1, HF/3-21G and B3LYP/6-31G(d) levels:
| Bond length / Å or angle / ° | Method | ||
|---|---|---|---|
| Semi-empirical/AM1 | HF/3-21G | B3LYP/6-31G(d) | |
| C1-C2 / C3-C4 | 1.382 | 1.370 | 1.383 |
| C2-C3 | 1.398 | 1.394 | 1.407 |
| C5-C6 | 1.383 | 1.376 | 1.386 |
| C1-C2-C3 / C2-C3-C4 | 121.2 | 121.5 | 122.0 |
| C1-C6 / C4-C5 (through space) | 2.119 | 2.210 | 2.272-2.273 |
The typical sp3 C-C bond length is 1.542 Å (for ethane) and sp2 C-C bond length is 1.47 Å (for butadiene). [8] The Van der Waals radius of a carbon atom is 1.70 Å. [9] The calculated C-C bond lengths at three different levels are shorter than sp3 and sp2 C-C bond lengths. However, the calculated C5-C6 bond length in ethylene fragment is slightly longer than the sp2 C-C bond length in ethylene (1.338 Å). [8] Calculated C1-C2 / C3-C4 bond lengths (where the C-C double bonds originally located) are shorter than literature sp2 C-C bond length for butadiene. The differences in the bond lengths between calculated and literature values can be attributed to the nature of the bonds in transition state. In the transition state, the C-C bond in ethylene fragment loses its double bond character (due to formation of σ bonds with terminal carbon atoms of cis butadiene) which leads to lengthening of its bond. For the cis butadiene fragment, the terminal C-C bonds also lose its double bond character and lengthening of C1-C2 / C3-C4 should be observed. The former case is indeed what is observed in calculation results. The calculated C1-C6 / C4-C5 bond lengths of the partly formed σ C-C bonds in the transition state are much longer than sp3 C-C bond length which indicates that σ C-C bonds are not readily formed in the transition state since the cis butadiene fragment needs to approach the ethylene fragment for σ C-C bonds formation.
Intrinsic Reaction Coordinate
IRC was calculated for the optimised transition state based on HF/3-21G level and N is set to be 50. The calculations for the IRC for the transition state can be found in the following link: DOI:10042/28075
The figures below show the IRC graph and its motion path to formation of product from the transition structure:
| IRC graph | Animation |

|
|
IRC calculations above show that the optimised transition structure does indeed lead to the formation of product via lowest energy pathway. The formation of two new σ bonds between the cis butadiene and ethylene fragments is synchronous as these two bonds are formed at the same time in a concerted fashion (as shown in the animation above).
Regioselectivity of the Diels-Alder Reaction
Introduction
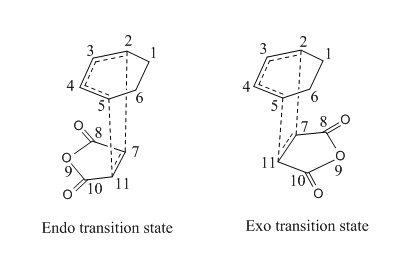
The figure below shows the reaction between cyclohexa-1,3-diene and maleic anhydride where two possible transition states can take place:
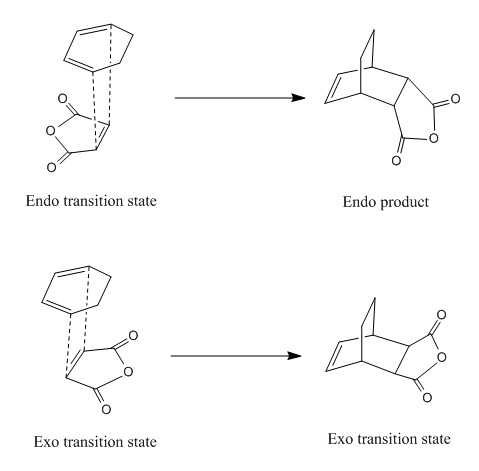
In the endo transition state, the maleic anhydride faces inwards that the anhydride group is directly beneath the diene. In the exo transition state, the maleic anhydride points outwards that the anhydride group is away from the diene of cyclohexa-1,3-diene. In this part of exercise, the structures of endo and exo transition state are investigated in terms of their energies, geometries and MOs.
Optimisation of Cyclohexa-1,3-diene and Maleic Anhydride Transition Structure
Both exo and endo transition states were created in GaussView and optimised by Gaussian at semi-empirical/AM1, HF/3-21G and B3LYP/6-31G(d) levels. The calculations for the optimisation,geometries, frequencies calculations and MOs of the transition states can be found from the links below:
For endo transition structure:
Semi-empirical/AM1: DOI:10042/28076
HF/3-21G: DOI:10042/28077
B3LYP/6-31G(d): DOI:10042/28078
For exo transition structure:
Semi-empirical/AM1: DOI:10042/28079
HF/3-21G: DOI:10042/28080
B3LYP/6-31(d): DOI:10042/28081
The table below shows the energies and imaginary frequencies obtained for optimised transition structures at different levels:
| Level | Endo transition state | Exo transition state | ||
| Energy / a.u. | Imaginary frequency / cm-1 | Energy / a.u. | Imaginary frequency / cm-1 | |
| Semi-empirical/AM1 | -0.05150480 | -806.41 | -0.05041904 | -811.56 |
| HF/3-21G | -605.61036797 | -643.50 | -605.60359122 | -647.33 |
| B3LYP/6-31G(d) | -612.68339658 | -446.93 | -612.67931094 | -448.47 |
From calculations above, it is clear that the endo transition state is thermodynamically more stable than exo transition state due to its lower energy with energy difference of 0.0040856 a.u. (or 2.563753255 kcal mol-1) at B3LYP/6-31G(d) level.
Imaginary Frequencies of Transition Structures
The figures below show the energies and imaginary frequencies of both optimised endo and exo transition structures at B3LYP/6-31G(d) level:
| Endo transition state | Exo transition state | |
| Energy / a.u. | -612.68339658 | -612.67931094 |
| Imaginary frequency / cm-1 | -446.93 | -448.47 |
| Front view | 
|
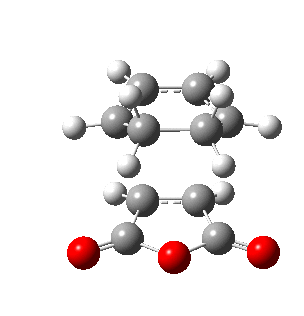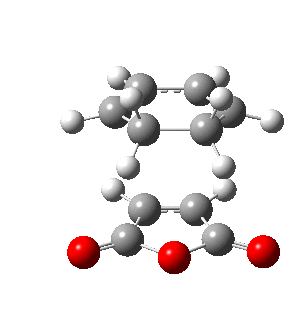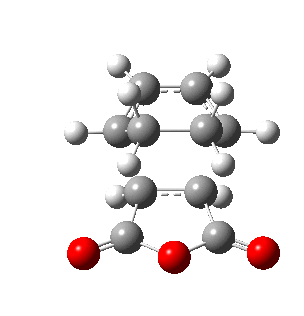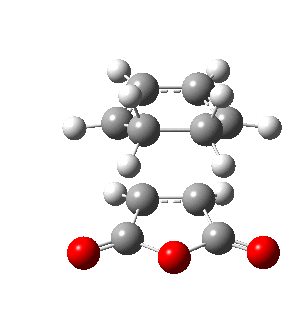
|
| Side view | 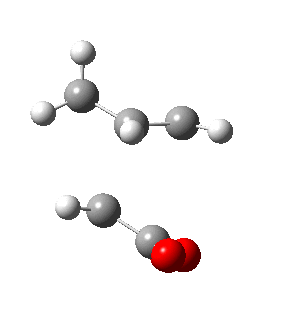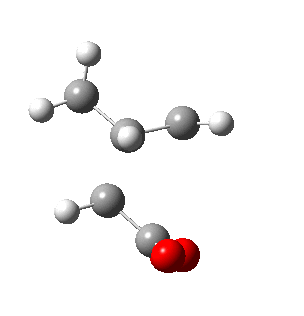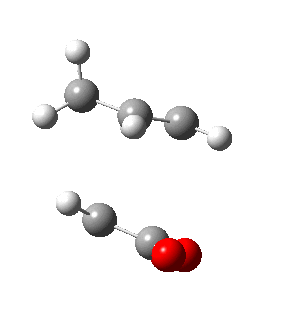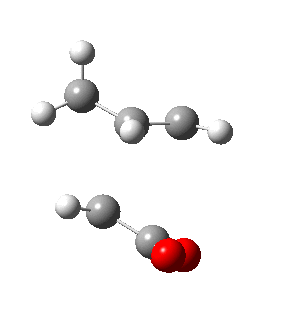
|

|
Negative frequencies obtained from optimisation of both structures indicate that the optmised structures are indeed transition states. Both motions involve the out of phase oscillation motions of atoms in cyclohexa-1,3-diene and maleic anhydride that form two new σ C-C bonds.
Geometries of Transition Structures
The table below shows the key bond lengths in both endo and exo transition states:
| Transition structure and calculation level | Bond length / Å | ||||||||||
| C1-C6 | C1-C2 / C6-C5 | C2-C3 / C5-C4 | C3-C4 | C2-C7 / C5-C11 (through space) | C7-C8 / C11-C10 | C7-C11 | C8-C9 / C10-O9 | O9-C4 / O9-C3 (through space) | O9-C1 / O9-C6 (through space) | ||
| Endo | Semi-empirical/AM1 | 1.523 | 1.491 | 1.393 | 1.397 | 2.162 | 1.489 | 1.408 | 1.409 | 3.313 | 4.678 |
| HF/3-21G | 1.560 | 1.518 | 1.371 | 1.396 | 2.230-2.232 | 1.481 | 1.370 | 1.394 | 3.100-3.101 | 4.535-4.536 | |
| B3LYP/6-31G(d) | 1.558 | 1.515 | 1.391 | 1.403 | 2.268-2.269 | 1.479 | 1.394 | 1.400 | 3.268 | 4.634 | |
| Exo | Semi-empirical/AM1 | 1.522 | 1.490 | 1.394 | 1.397 | 2.170-2.171 | 1.488 | 1.410 | 1.409-1.410 | 4.536-4.537 | 3.342-3.347 |
| HF/3-21G | 1.559 | 1.519 | 1.370 | 1.398 | 2.261 | 1.481 | 1.373 | 1.396 | 4.447 | 3.188-3.189 | |
| B3LYP/6-31G(d) | 1.558 | 1.514-1.515 | 1.391 | 1.403 | 2.290-2.291 | 1.479 | 1.398 | 1.400 | 4.562 | 3.334 | |
Based on calculations at B3LYP/6-31G(d) level which is higher level of theory than semi-empirical/AM1 and HF/3-21G levels, the geometries of both transition states are similar except in the through space bond distances. First, the through space C2-C7 / C5-C11 bond distance in endo transition state is shorter than that in exo transition state which indicates that the σ C-C bonds are more likely to form in the structure. Second, there is steric repulsion between O9 and C3-C4 fragments in endo transition state and between O9 and C1-C6 fragments in exo transition state. This effect seems to be more enhanced in endo transition state as the through space O9-C4 / O9-C3 bond distance is slightly less than through space O9-C1 / O9-C6 in exo case. However, secondary orbital interactions between the π systems of -CH=CH- and -(C=O)-O-(C=O)- fragments play an important role in negating the steric repulsion effect in endo transition state.
MOs of Transition Structures
The figures below shows the HOMO, HOMO-1 and LUMO of optimised endo and exo transition states which were calculated at HF/3-21G level:
| Endo transition state | Exo transition state | |||||
| HOMO | HOMO-1 | LUMO | HOMO | HOMO-1 | LUMO | |
| Front view | 
|

|

|

|

|
|
| Side view | 
|

|

|

|

|
|
The endo transition state is thermodynamically stable and hence preferred over exo transition state in Diels-Alder reaction due to lower in energy as stated in optimisation section. The lowering of energy may be due to secondary orbital effect interaction between the the π systems of -CH=CH- fragment in cyclohexa-1,3-diene and -(C=O)-O-(C=O)- fragment in maleic anhydride of endo transition state which can stabilise the overall structure. This effect can be seen in the HOMO-1 orbital of endo transition state where there are favourable orbital interactions between -(C=O)-O-(C=O)- and -CH=CH- fragments (shown in the red parts). This is in contrast with HOMO-1 observed in the exo case where there are no favourable orbital interactions in -(C=O)-O-(C=O)- fragments.
References
- ↑ R. Hoffmann and W. D. Stohrer, "The Cope Rearrangement Revisited", J. Am. Chem. Soc., 1971, 93, 6941–6948. DOI:10.1021/ja00754a042
- ↑ O. Wiest, K. Black, and K. Houk, "Density Functional Theory Isotope Effects and Activation Energies for the Cope and Claisen Rearrangements", J. Am. Chem. Soc., 1994, 116, 10336-10337. DOI:10.1021/ja00101a078
- ↑ D. Hrovat, B. Beno, H. Lange, H. Yoo, K. Houk, and W. Borden "A Becke3LYP/6-31G* Study of the Cope Rearrangements of Substituted 1,5-Hexadienes Provides Computational Evidence for a Chameleonic Transition State", J. Am. Chem. Soc., 1999, 121, 10529-10537. DOI:10.1021/ja990476m
- ↑ G. Schultz and I. Hargittai, "Conformational investigation of gaseous 1,5-hexadiene by electron diffraction and molecular mechanics", Journal of Molecular Structure, 1995, 346, 63–69. DOI:10.1016/0022-2860(94)09007-C
- ↑ D. Hrovat, J. Chen, K. Houk, and W. Borden, "Cooperative and Competitive Substituent Effects on the Cope Rearrangements of Phenyl-Substituted 1,5-Hexadienes Elucidated by Becke3LYP/6-31G* Calculations", J. Am. Chem. Soc., 2000, 122, 7456-7460. DOI:10.1021/ja000531n
- ↑ E. Brown, D. Henze, and W. Borden, "Are 1,5-Disubstituted Semibullvalenes that Have C2v Equilibrium Geometries Necessarily Bishomoaromatic?", J. Am. Chem. Soc., 2002, 124, 14977-14982. DOI:10.1021/ja027392p
- ↑ K. Houk, J. González, and Y. Li, "Pericyclic Reaction Transition States: Passions and Punctilios, 1935-1995", Acc. Chem. Res., 1995, 28, 81-90. DOI:10.1021/ar00050a004
- ↑ 8.0 8.1 H. Bernstein, "Bond Distances in Hydrocarbons", Trans. Faraday Soc., 1961, 57, 1649-1656. DOI:10.1039/TF9615701649
- ↑ A. Bondi, "van der Waals Volumes and Radii", J. Phys. Chem., 1964, 68, 441–451. DOI:10.1021/j100785a001