Rep:Mod:fjm19883
Cope rearrangement tutorial
Optimizing the reactants and products
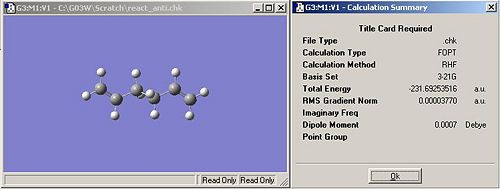
The optimised version of the 1,5-hexadiene with anti linkage in the central four C atoms is shown in the image below. It can be seen from compairing the optimised stucture that it has been optimised to the lowest energy of the anti 1,5-hexadienes. This the the anti2 conformation. The energy can be seen in the summary as -231.69254 hartrees. Symmetrizing the molecule gives it a point group of Ci/C1.
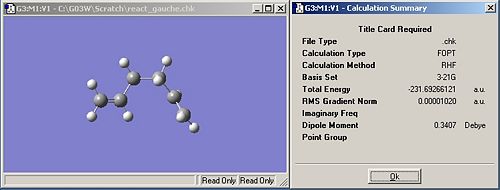
The optimised version of the 1,5-hexadiene with gauche linkage for the central four C atoms is shown in the image below. This has also optimised to the lowest of the 4 gauche stuctures. This is the gauche3 conformation. This is lower in energy than the anti conformer by a relative amount of 0.04kcal/mol. This is what was expected... The symmetry of this molecule is C1.
It can be seen from the optimisations carried out above that the lowest energy conformation has been found already. As gaussian will optmise to the lowest energy stucture, and the gauche is lower in energy, then the gauche3 conformation is the lowest in energy.
The anti2 conformation has already been found from the optimisation above. It does have the Ci point group and also the same energy of -231.69254 hartrees that is shown in appendix 1.
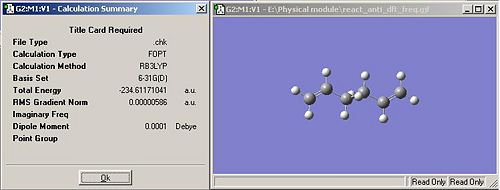
The final optmisation of the anti conformer can now be further optimised using the B3LYP/6-31G* basis set. This gives a final energy of -234.61171 hartrees. This means it actually has a higher energy than when using the lower accuracy basis set, however the optimised molecule that has been obtained will be closer to the literature values for the molecule. The dipole moment for this further optimisation can been seen to be much smaller, 0.0001 rather than 0.0007. The geometry of this molecule has not changed much at all, then how it was before the optimisation. For example the dihedral angle of the central 4 C atoms was 180degrees for the first optmisation, and was 179.994degrees after the 2nd optimisation.
I then ran a frequency calculation on the B3LYP/6-31G* optimised molecule. This produced the following IR spectrum. It can be seen that there are no imaginary frequencies, as these are negative frequencies and only positive, real frequencies are shown on the spectrum.
The energies of the molecule could then be obtained so it is possible to compare them to experimental values.
| Electronic energy | Sum of electronic and zero point energies | Sum of electronic and thermal energies | Sum of electronic and thermal enthalpies | Sum of electronic and thermal free energies | |
| Anti2 | -234.611710 | -234.469204 | -234.461858 | -234.460913 | -234.500777 |
| Anti2 from appendix | -234.611710 | -234.469203 | -234.461856 |
It can be seen that the values I obtained are correct to 5d.p when compared to the values in the appendix. This difference is negligible, so I can be assumed that the molecules I obtained are the full optimised molecules.
Optimising the ‘chair’ and ‘boat’ structures
Firstly I optimised a CH2CHCH2 fragment using the HF/3-21G method, this gave the following optimised molecule.
I then placed two of these molecules on top of each other with the terminal ends 2.2Å apart. This arrangement could then be optimised using the TS(Berney) optimisation job type. I made sure to enter opt=noeigen into the additional keyword box as this made sure that Guassian only looked for one transition state. This gave optimised bond lengths of 2.02043Å. Looking at the IR of the optimised molecule it can be seen that there is an imaginary frequency at 818cm-1. It can be animated to show the vibration of this frequency as seen below. This vibration responds to the Cope rearrangement, as it shows how one of the bonds is formed from the terminal ends of the allyl fragments.
-
First chair optimisation
-
Imaginary frequency vibration
I then used the freeze coordinate method to optimised the transition state, I set the bond lenths to 2.2Å. The final molecule can be seen below. The forming bond lengths are exactly 2.2Å as shown in the image. These bond lengths can now also be optimised by setting them to derivatives with no set bond length. This gave the final output that is shown below. It has forming bond lengths of 2.02073Å, which is roughly the same as in the initial optimisation. This shows that the 1st method used is actually quite accurate for a molecule this size.
-
Chair with set bond length
-
Chair with optimised bond length
The energies of the different methods can be seen in the table below.
| Method | Energy |
| Initial TS(Berny) | -231.61932244 |
| Freeze coordinates | -231.61518541 |
| Derivative | -231.61932239 |
It can be seen from these values that actually the lowest energy method is the first method used without freezing the coordinates or changing the bonds to derivatives. However the initial calculation and the last calculation are the same to 6d.p so can be looked at as being close enough to give the same optimised molecule. This shows that the first calculation was actually very accurate in this case. However this probably is only the case as it is a very simple molecule. In more complicated transition structures the derivative method would have to be used.
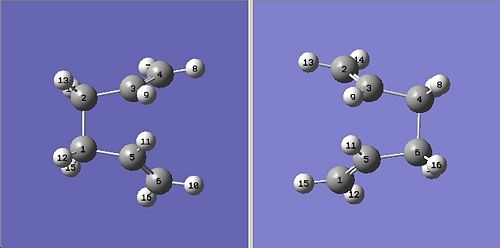
I set up the boat transition structure so that the QST2 method could be used. I renumbered the reactant and product as shown below. It was important to make sure that the renumbering was done in order, starting from the bottom of the molecule working up, this is because the computer automatically changes numbers as soon as one number is changed. I renumbered the carbon atoms first, as this made it easier to then renumber the hydrogens to correspond with new carbon numbering.
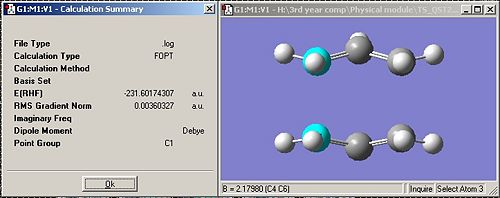
I then optimised using the QST2 also making sure that I entered opt=full into the additional keywords box. This gave the following transition state:
It can be seen that the bond lengths for the breaking/forming bonds is 2.17980Å which is longer than the 2.02073Å obtained for the chair structure. This shows that either the QST2 method is more accurate as the value is closer to the 2.2Å expected, or that in the boat transition stucture the bond lengths should be longer than in the chair transition state.
I carried out an IRC calculation in the forward direction so it was possible to work out which conformers they connect. This was done by running the IRC calculation computing 50 points. Then using the output of this calculation optimising it to a minimum using the Hartree-Fock 321G basis set. This gave a final output for the chair shown below.
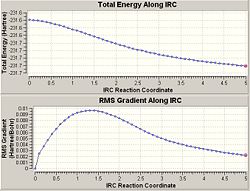
The energy of this was -231.69167Hartrees which when compaired to Appendix 1 can be seen to be the Gauche2 conformer.
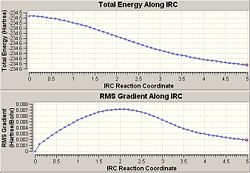
The energy of this was -231.69266 which when compaired to Appendiz 1 can be seen to be the Gauce3 conformer. The graphs from the IRC sohw the energy as the reaction is taking place. It shows that the energy is reduced as it should be when the reaction takes place. However it shows that neither of the IRCs have produced the lowest energy final product as the gradient has no reached 0 which would show a minimum energy. Therefore the second optimisation of the molecule given by the IRC is needed to produce a final optimised product. I used this method, as I found that the IRC would not carry on to completion if I tried to compute force constants at every step.
I then optimised both the chair and the boat stuctures using the B2LYP/6-31G* method. This gave the following stuctures and energies.
-
Higher optimisation of chair
-
Higher optimisation of boat
Compairing the higher optimised structures to the HF method it can be seen that the molecules have not changed geometry much with different methods. For the chair transition state the breaking/forming bond length has been reduced to 1.96907Å from the original 2.02073Å. The boat bond length has been increased to 2.20611Å from the original 2.17780Å. This concludes that in the boat transition structure the bond breaking/forming lengths are longer than for the chair transition structure.
| HF energy | B3LYP energy | |
| Chair | -231.61932239 | -234.55698279 |
| Boat | -231.60174307 | -234.54309303 |
Looking at the energies obtained for the different methods there is a substantial difference in the energy for the lower optimisations and the higher. The higher optimisations give a much lower energy, proving that they are the more accurate transition structures.
| Chair TS | -234.409015
| |||||
| Boat TS | -234.396004
|
Using the thermochemistry values show above that can be found in the thermochemistry section of the output file, it is possible to work out the activation energies of the boat and the chair structures. This is done by working out the difference in energy between the starting material (Anti2 conformer) and the transition structures. The values worked out are shown in the table below.
| Activation energy | Literature 0K | |
| Chair 0K
Chair 298.15K |
34.0525425
33.1589825 |
33.5 ±0.5 |
| Boat 0K
Boat 298.15K |
41.9590425
41.323385 |
44.7±2 |
Compairing the calculated activation energies to literature values it can be seen that the chair activation energy is 0.05kcal/mol above the experimental findings, and the boat structure is 0.74kcal/mol below the experimental value. Therefore the chair structure has produced a better approximation that the boat structure. As expected the activation energies for the reaction at 298.15K are substantially lower than at 0K.
Diels alder cycloaddition
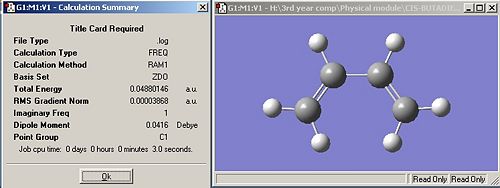
I optimised a cis-butadiene molecule using the AM1 semi-empirical molecular orbital method to give the following structure:
Computing MOs gave the HOMO and LUMO in the pictures below. The HOMO of the cis-butadiene is anti-symmetric in respect to the plane, this can be worked out as there is a mirror plane running down the centre of the molecule. This is as expected for a butadiene molecule.
-
Cisbutadiene HOMO
-
Cisbutadiene LUMO
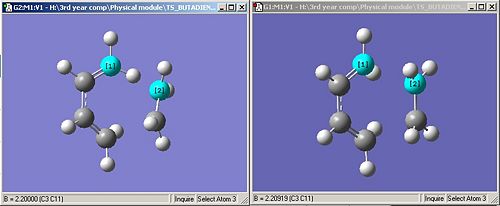
To compute the transition structure I placed the ethylene fragment, CH¬2CH2, about 2.2A above the bond breaking/forming carbons on the cis-butadiene. I then calculated the transition structure by setting the bond lengths to 2.2A and running a TS(Berny) calculation. The product can be seen below. The bond lengths can be optimised to give the final product shown in the right-hand picture.
Endo |
The literature bond lengths are: sp3 C-C bond length ethane=1.536A [1] sp2C-C bond length ethene = 1.330A
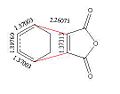
The bond lengths of the partially formed C-C bonds can be seen to be 2.20919A. The outer C-C bond length on the cis-butadiene is 1.37003A and the central C-C bond length is 1.39452A. This shows that in the transition structure the outer C-C bond has more sp3 and therefore double bond character than the inner C-C bond as it has a shorter bond length. As the inner C-C bond length is higher, but still a lot closer to the sp2 than sp3 bond length it must have double bond character but not as much as the outer C-C bond. Therefore the transition state is closer in geometry to the reactants rather than the products. The Van der Waals radius of a carbon atom is 1.7A, as the bond breaking/forming length is 2.20919A it shows that the carbons are not just being brought close together due to Van der Waals forces, they are going to form a bond.
The vibration that corresponds to the reaction path Is shown below, this is the imaginary frequency. It shows that the transition structure is correct as the vibration is showing the formation of C-C bonds. The forming of these bonds in synchronous as the vibration is completely symmetrical and the bonds are forming at exactly the same time.
The imaginary vibration can be compaired to the first positive vibration. This is shown in the picture below. This is not a bond forming vibration as the carbons from the two different molecules do not get any closer together. It is also not symmetric down the mirror plane as the ethylene is swinging from side to side on an axis
The HOMO of the transition structure is anti-symmetric as has no mirror plane. The LUMO can be seen to be symmetric. The HOMO is formed from the HOMO of the cisbutadiene which is anti-symmetric and the anti-symmetric LUMO of the ethylene. Therefore the reaction is allowed as the bond is formed from two anti-symmetric MOs, a HOMO and a LUMO, to give a anti-symmetric HOMO.
The LUMO is made up of the cis-butadiene LUMO and the ethylene HOMO to produce the symmetric MO than can be seen in the picture.
-
Transition state HOMO
-
Transition state LUMO
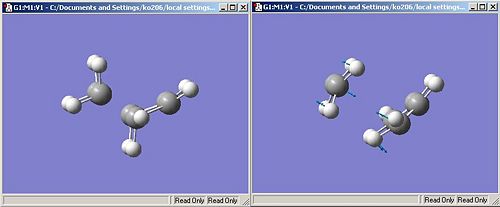
I worked out the transition states in the same way as for the above transition state. I froze the coordinates to 2.2A and carried out a TS(Berny)optimisation. I then optimised the bond lengths with the same method and basis set. This gave the transistion structures shown below.
Endo |
Exo transition structure
Endo |
Endo transition structure
The imaginary vibrations can be used to prove that it is infact the right transition structures I have found. The pictures below show that the imaginary vibrations show the bond forming of the correct carbons, as the vibration shows the bond breaking/forming lengths getting shorter. The bonds are formed synchronously as are both formed at same time.
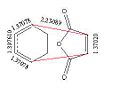
The diagrams below show the relevant C-C bonds in the two transition states. The cyclo-hexa-1,3-diene still has the two double bond character as these bonds are around 1.27A which is comparable to the 1.33A expected of a C=C bond. The new double bond that is forming is around 1.397A for both structures, this means that it is closer to a double than single bond, but as the bonds are not as short it doesn’t show full double bond character yet. The maleic anhydride still has most of its double bond character in both the endo and the exo transition states, as it as has short 1.37A bond length. The bond breaking/forming length is significantly larger for the exo than the endo form. This can be explained by also looking at the C-C distances between the C=O-CO-C=O fragment on the maleic anhydride with the C atoms on the CH2CH2 fragment for exo and endo. These distances are 2.9163A for the exo and 2.8476A for the endo. This shows that in the exo transition structure the two starting materials are much further apart than in the endo. This is due to the interaction of the Hs in the CH2CH2 with the C=O-CO-C=O fragment. In the endo form these hydrogen’s are much closer to the maleic anhydride which is not energetically favourable. Therefore the structures are orientated further away from each other to minimise the steric hindrance.
-
Exo TS bond lengths
-
Endo TS bond lengths
The MOs of the two transition structures can be analysed to back up this theory. In the exo HOMO there is destructive interference between the orbital’s on the O of the maleic anhydride and the orbital’s of the CH2CH2 as nodes are formed between the orbital’s of difference parity. Therefore the two starting materials will want to be further away from each other to decrease the instability. In the endo HOMO there is secondary overlap which causes stabilisation. This is because the MOs of the O on the maleic anhydride interact with the MOs of the CHCH fragment, with favourable overlap between the MOs with the same parity. This will mean the two reactants will want to be closer together to maximise this secondary orbital overlap. These arguments also explain the difference in energy of the two structures with endo having the lower energy of -605.60359 and exo of -605.610368.
-
Exo HOMO
-
Endo HOMO
References
- ↑ Organic Chemistry, G. Marc Loudon – 2007