Rep:Mod:filmubs278m3

The Cope Rearrangement Tutorial

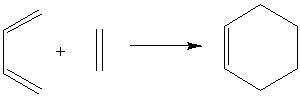
The Cope rearrangement of 1,5 heaxadiene is an example of [3,3] sigmatropic rearrangement. Such reactions can proceed via two routes or transition states, either a chair-like structure or the boat-like structure. The aim of this part of the exercise is to find the lowest energy conformations for the transitions state structures for 1,5 hexadiene.

Part A) and B)-

For part A, an anti-periplanar conformation for 1,5 hexadiene molecule was created using Gaussview by ensuring to set the dihedral angle (carbons 2-3-4-5) to 180 degrees. This structure was then optimized using the Hartree-Forck method and 3-21G as the basis set.

For part B), a ‘gauche’ conformation for 1,5 hexadiene was created, this time by ensuring to set the same dihedral angle to 60 degrees. The structure was also optimized using the same method as before.

The table below shows some do the details of the 2 conformers and compares them to those found in Appendix 1.

	Anti	Gauche
JMOL
Energy(Hartree)	-231.69260	-231.69167
Point group	C2	C2
Corresponds to	anti 1	gauche 2

You can see that, the Anti 1 conformation is slightly lower in energy than the gauche structure (by 0.001 Hartree or 2.44 kJ/mol. It is naturally expected for the anti conformations to have lower energies/be more stable than the gauche conformations due to the lack of steric clash between the large CHCH2 groups as a result of the larger dihedral angles.

Part C) D) and E)

To find the conformer with the lowest energy, the Anti and gauche structures above, were manipulated slightly and their structures optimized using the same method as before. There point groups were also noted and everything was compared to Appendix 1.

	Anti 2	Gauche 4	Gauche 3
JMOL
Energy(Hartree)	-231.69254	-231.69153	-231.69266
Point Group	Ci	C2	C1

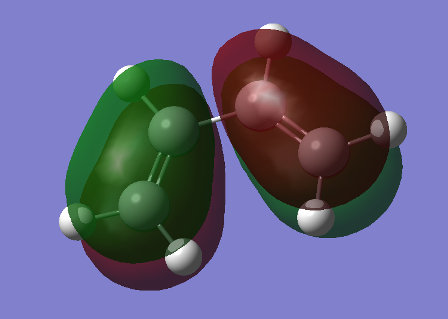
Our findings would suggest the gauche 3 conformation is the one with lowest energy. However, as we’ve encountered before, this is not the expected result. To explain this, we ran an energy calculation setting the population to [pop=full] and analysing the resulting MOs for the two lowest anti and gauche conformers we’ve created, anti-1 and gauche 3. The HOMO orbital for the 2 conformers is shown below.

We can see that in the gauche 3 structure there is a significant interaction between the pi-bonds of the alkenes, which isn’t present in the anti-1 HOMO. This interaction or overlap allows for the molecule to be more stable in this conformation.

All the energies and point groups for the conformations found above match those in Appendix 1.

Part F)

Here, the anti 2 structure is re-optimized using DFT B3LYP as the method and 6-31G as the basis set. The tables below compare the 2 optimizations and the difference made on the Anti2 conformation in terms of energy and geometry.

Anti 2 (HF/3-21G)Summary

Dihedral Angle	180.0
Energy (Hartree)	-231.69254
Point Group	Ci

Anti 2 (DFT-B3LYP/6-31G(d)) Results Summary

Dihedral Angle	180.0
Energy (Hartree)	-234.6117
Point Group	Ci

Part G)

Frequency analysis was carried out on the B3LYP optimized structure and the using the resulting log file, the following list of energies was found at 298K.

Sum of electronic and zero-point Energies=           -234.416244
Sum of electronic and thermal Energies=              -234.408954
Sum of electronic and thermal Enthalpies=            -234.408010
Sum of electronic and thermal Free Energies=         -234.447849

Optimizing the ‘Chair’ and ‘Boat’ Transition structures

This part of the exercise will be looking at computing the transition state structure using different methods.

Part A)

Firstly, the allyl fragment (CH2CHCH2) was drawn on Gausview and copy of it was made so there were two allyl molecules in the one window. The fragments where then manipulated so that they resemble the chair transition state in Appendix 2, with the distances between the terminal carbons as 2.2 A. This was our guess for the chair transition state.

Part B)

All calculations from here up to and including Part F was calculated using Hartree-Fock as the method and 3-21G as the basis set.

Using a copy of our guess chair structure, an optimization and frequency was run in two different ways.

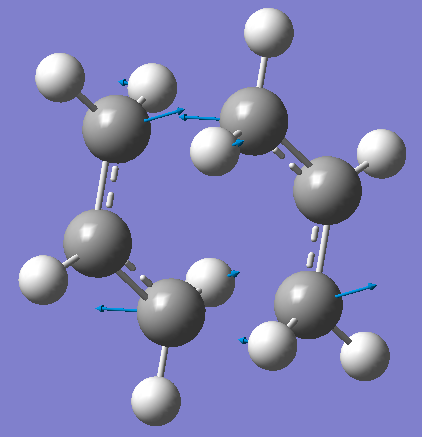
For the first calculation the Opt+Freq is chosen for the job type, and the optimization set to TS (Berny) and with the additional words Opt=NoEigen. As we’re looking into transition states, we expect there to be a single negative /imaginary frequency. All positive frequencies would indicate the minimum energy possible for the molecule of that conformation and we expect that to be the final product. For this calculation we find one that there is one negative/imaginary frequency at 817.9 cm-1, and this vibration is illustrated below.

Part C) and D)

The second calculation is generated by freezing the reaction coordinates, minimizing the rest of the molecule, and optimising the relaxed structure again. The table below shows the major differences between the two methods of calculation.

	Force Constant Method	Reaction Coordinate Method
Energy (Hartree)	-231.61932	-231.61932
Point Group	C2h	C2h
C=C bond length	2.02A	2.02A
Negative frequency (cm-1)	-871.91	-818.03

In the second method, using the Redundant Coord. Editor, the terminal carbons involved in the bonding between the two fragments were selected and the bond coordinate was set 2.2 A. this was then frozen and optimized using the HF/3-21 method and basis set along with the additional words opt=modredundant. The resulting file was then edited again, by selecting a new coordinate and setting it to 'derivative' instead of Add for each bond. This is then optimized again.

Part E)

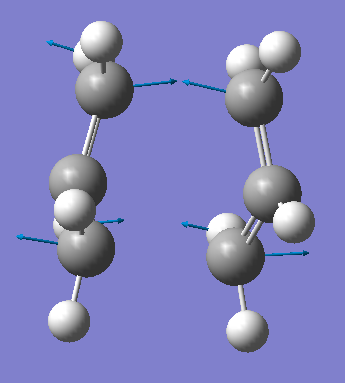
Now it’s time to optimise the geometry of the boat transition structure. You can do this by setting up the reactants and products using the Anti-2 structure created previously ensuring the entire number labels match. This is run for optimization and frequency and use TS (QST2) as the job type. This job fails and the resulting structure is shown below.

We can see from that structure that the calculation linearly interpolated between the reactants and products without considering rotation around the bonds. Instead, we can help get to the right boat structure by adjusting the starting molecule. Both the reactants and products dihedral angles were changed from nearly 180 degrees to 0. Then the interior angles of this boat-like structure are then changed from about 112 to 100 degrees. The optimization was then run again and it was successful.

Part F)

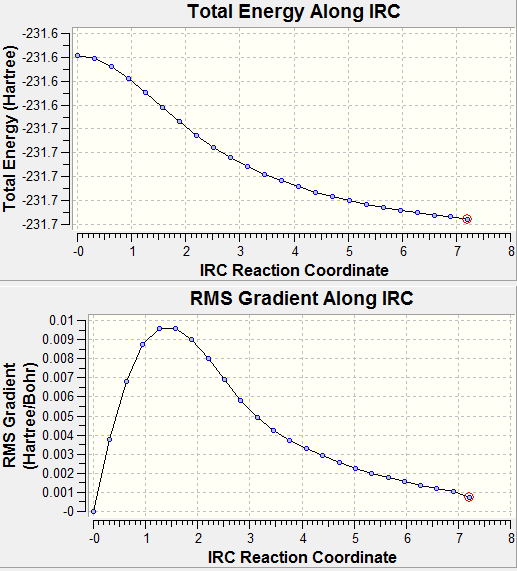
The IRC, Intrinsic Reaction coordinate method allows you to follow the minimum energy path of the transition structure. For both the boat and chair (optimized) structures were run by Gaussian using the Job Type IRC and setting it the forward, calculate constants once and changing the no. of points to 50. This however failed to give the minimum energy. So instead, the calculate constants tab was changed to always and the no. of points increased to 75. These were then run using the SCAN servers.

As it is not possible to tell from the transit states themselves which product they would result in, we use another method call the Intrinsic Reaction Coordinate method. Here, Gaussian takes small geometry steps to the direction where the energy gradient is the steepest.

To apply this method to both our structures, we selected IRC under Job type in the Gaussian calculation menu. As our R.C is symmetrical we set it to compute in the forward direction. Now we have the option of how we want to calculate our force constants, once, at every step or read them from the .chk file. Using the first option, the minimum energy was not reached so in order to get a more accurate result, the second method was then employed and the number of points to 75. This was then sent to SCAN.

Chair TS-

Boat TS-

Part G)

To find out which of the two TS has the lower activation energy barrier, and hence the correct TS, we need to compare the difference in energy between each of the chair and boat conformers and the reactant (Anti 2).

	HF/3-21G			B3LYP/6-31G(d)
	Electronic energy/a.u.	Sum of electronic and zero-point energies/a.u.	Sum of electronic and thermal energies/a.u.	Electronic energy/a.u.	Sum of electronic and zero-point energies/a.u.	Sum of electronic and thermal energies/a.u.
		0 K	298.15 K		0 K	298.15 K'
Chair TS	-231.6193	-231.4667	-231.4604	-233.2918	-233.1483	-233.1426
Boat TS	-231.6028	-231.4509	-231.4453	-233.2760	-233.1337	-233.1276

Looking at the table above and as the Anti 2 conformer has a lower energy than both the transition states, we can see that the energy difference is less between the reactants and Chair TS than the Boat TS and reactants (all the energies for the chair conformation are lower than that of the boat conformation). That is the activation energy barrier for the chair conformation is less and hence the reaction proceeds via the chair transition state.

Diels Alder Cycloaddition

Part i)

Cis-butadiene and ethane were both created by Gaussian and optimized using AM1 as the method.

Cis-butadiene-

Ethene-

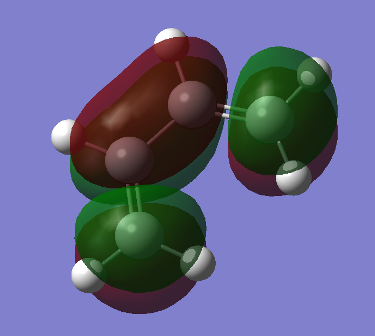
From the diagrams above we can see that cis-butadiene’s HOMO has an a symmetry, whilst it’s LUMO has an s symmetry. The inverse is true for ethene. This means that the HOMO of butadiene will interact with the LUMO of ethene in order to form the cyclohexadiene.

Part ii)

The guess transition state was built using the methods employed before, and this was optimized set to TS-Berny, and the method as AM1.

To ensure that this was indeed, the transition state we looked at the vibrations and once again, there was only one negative/imaginary frequency at -956.2 cm-1.

This vibration has an s symmetry whilst the one at 147.3 cm-1., which is the lowest positive frequency as an 'a' symmetry.

The table below shoes the bonds lengths in comparison to those in the literature.

Bond lengths

Bond	Bond Length Calculated	Bond length (normal)
C-C (being formed)	2.12Â	1.54Å
C=C ( in Cis-Butediene)	1.38Â	1.32Å
C=C (in formation of cyclohexene)	1.40Â	1.32Å

As you can see the C-C single bond here is longer than what was recorded in the literature. This is because in TS the sigma bond is not fully formed yet. The C=C of double bonds breaking in cis-butadiene are also a little longer than the average C=C bond length. This is because it’s forming a C-C single bond which is longer than the C=C bond. Likewise, in the formation of the double bond in cyclohexene, the C=C bond recorded is longer than the normal C=C bond, this is because it’s still ‘shortening’ to form the C=C bond from the original C-C bond.

Part iii)

Cylcohexa-1,3-diene reacts with maleic anhydride in the same mechanism as that of the Diels Alder reaction. This reaction however can produce two products, the exo and endo product and the aim of this exercise to understand the regioselectivity of this reaction.

Experimental results tell us that although the exo product is lower in energy, the major product of this reaction is the endo product. This means that that the reaction is under kinetic control. This in turn means that the endo product, the kinetic product has a more stable TS with a lower activation barrier. To test this, we need to find out the energies for both TS. Both transition states were built using Gaussian as before and the guess structures optimized to TS Berny with AM1 as the method.

T.S	Energy (Hartree)
Exo	-0.05042
Endo	-0.06478

These results show that Exo transition state is higher in energy explaining the favouritism towards the formation of the Endo transition state and hence the endo product. This favouritism is also known as the endo-rule. The secondary orbital interactions between teh conjugate groups in the dienophile and the back of the diene result in the stability of the endo transition state. This transition state exhibits bonding interactions whilst the exo transition state exhibits anti-bonding interactions. The second reason is the steric clash. In the exo transition state experiences steric repulsion as a result of the oxygens and the CH2 groups. This strain results in a greater energy for the TS.

Looking at the HOMO of the exo and endo TS we do not see much secondary orbital interaction, which would lead us to believe that for this reaction, the steric strain in the exo transition state is the primary reason for the increased energy of that TS.