Rep:Mod:filmubs278
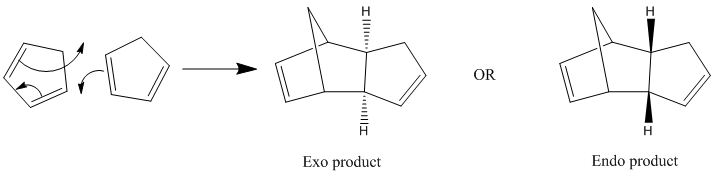
Section 1A- The Dimerization of Cylcopentadiene
Cyclopentadiene is an organic compound that can act as a diene and a dienophile. At room temperature it can dimerize into dicylopentadiene via a Diels Alder reaction. This reaction can result in two isomers, the endo product or the exo product as shown below.
The two possible products were modelled using ChemBio3D Ultra and their energies minimised using the MM2 force field. This force field method....
| Exo Product (1) | Endo Product (2) | ||||
| Exo product energies (kcal/mol) | Endo product energies (kcal/mol) | |
| Stretch | 1.2829 | 1.2713 |
| Bend | 20.5879 | 20.8547 |
| Stretch-Bend | -0.8341 | -0.8382 |
| Torsion | 7.6718 | 9.5037 |
| Non 1,4 VDW | -1.4355 | -1.5105 |
| 1,4 VDW | 4.2324 | 4.2881 |
| Dipole/Dipole | 0.3778 | 0.4447 |
| Total Energies | 31.8832 | 34.0139 |
Analysis
From the table above, we see that the exo dimer (1) has a lower overall energy than the endo product (2). This means that the exo product is the more stable one and the thermodynamic product. However, experimental results show that the endo dimer, the kinetic product, is the major product of this reaction. From this we can say that this reaction is under kinetic control.
Although the kinetic product has a higher energy than the thermodynamic product, it also has a more stable transition state with a lower activation barrier. This favouritism for the more stable transition state in Diels Alder reactions is also known as the endo rule.
The stability of this transition state is due to the secondary orbitals interaction between the conjugate group in the dienophile and the back of the diene. In the case of the endo product, these interactions are bonding interactions whilst the exo-transition state exhibit antibonding interactions as illustrated in the diagram below.1
| Secondary orbital interactions leading to the Endo Product (2) |
|
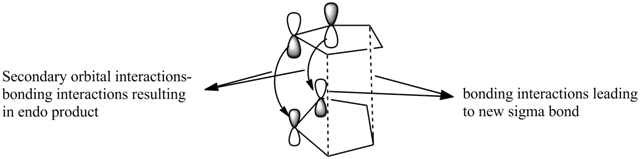
Section 1B- The Hydrogenation of Cyclopentadiene Dimer
The hydrogenation of the resulting endo dimer in the previous reaction can give two possible products where the either one of the double bonds is replaced with 2 hydrogens.
| Product 3 energies (kcal/mol) | Product 4 energies (kcal/mol) | |
| Stretch | 1.2794 | 1.0963 |
| Bend | 19.0909 | 14.5074 |
| Stretch-Bend | -0.8432 | -0.5.493 |
| Torsion | 11.1365 | 12.4972 |
| Non 1,4 VDW | -1.6454 | -1.0507 |
| 1,4 VDW | 5.7864 | 4.5124 |
| Dipole/Dipole | 0.1622 | 0.1407 |
| Total Energies | 34.9668 | 31.1540 |
| Models |
Looking at the energies in the table above, product 4 has a lower energy than product 3 by approximately 3.8 kcal/mol. As a result, product 4 – the thermodynamic product- would be the major product of this reaction.
Analysis
From the table, we can see that the greatest difference in the 2 products is as a result of the ‘bending’ energy. As the results given by the MM2 calculation represents the extent of deviation from the ideal configuration, these bending energy values represent the bending strain as a result of the deviation from the ideal configuration or orientation of the atoms. To investigate this deviation, it’s important to consider the bond angles as well as the ‘rigidity’ of the molecule.
The following snapshots taken of product 3 and 4 after using ChemBio3D to measure the angles. Buttons linking to the rotatable structures can also be found in the table below.
| Product (3) | Product (4) |
 |
|
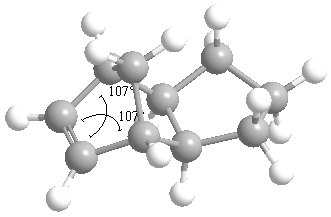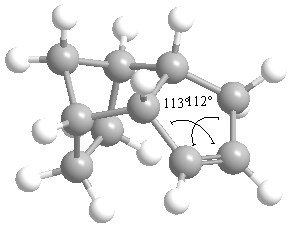
| Angle= 107° | Angle= 112.5° (average) |
The bond angle of the carbon-carbon double bond in product 3 is 107 whilst the bond angle in product 4 is (on average) 112.5. The bending energies produced earlier reflect the deviation of these bond angles from the ideal angle of 120 degrees. This means that product 3, with the greater deviation from the ideal carbon-carbon double bond angle would be more strained and the minor product of the reaction. Consequently, product 4, the less strained molecule would be the major product.
Another possible factor to consider is the rigidity of the molecule. Having the double bond on the same side/ring as the bridging group would make the molecule less flexible than if it were in 5-membered ring and hence higher in energy as seen in product 3. This could also explain why product 4, the thermodynamic product is the major product of this reaction.
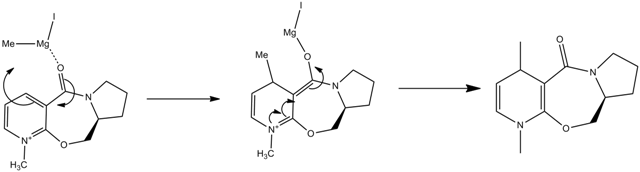
Section 2- Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
Reaction of Prolinol (5)
In this section, we are going investigate the stereoselectivity of the reaction of prolinol (5) with a Grignard reagent to form product (6). We also look into the stereocontrol involved in the formation of product (8) from (7).
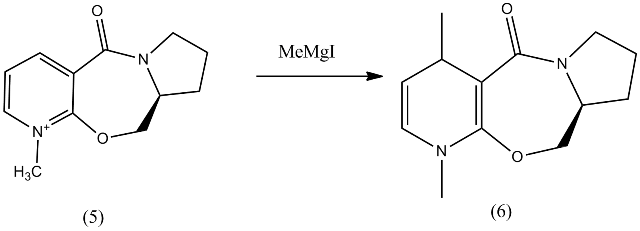Firstly Prolinol (5) was modelled using ChemBio3D and its geometry minimized using the MM2 force field.
Having tried a number of possible confirmations, the following molecule and energy was the lowest found for Prolinol (5). This conformation will react with MeMgI to form product (6).
| Prolinol (5) | Product (6) |
| Total Energy: 43.1626 kcal/mol | Total Energy: 37.4394 kcal/mol |
To understand the selectivity in the formation of product (6) we need to look at both the structure of the molecule and the position of the carbonyl group as well as the reaction mechanism.
From the above image we can see that the carbonyl group is slightly tilted so that it’s at a higher plane than the rest of the aromatic rings. Considering the mechanism above, the coordination of the Mg with the carbonyl group would result in the addition of the methyl group on the same face as that of the carbonyl-Mg coordination.
Reaction of Molecule 7
In this molecule, coordination with the carbonyl group means that the NHPh group would had on the opposite face.
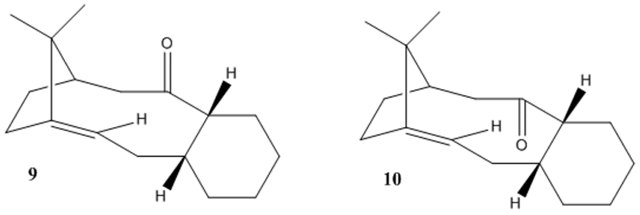
Section 3- Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
Using ChemBio3D and the MM2 force field, the lowest energies for intermediate 9 and 10 were found. This required constant manual editing of the position of the molecules to achieve the conformation with the lowest energies. Changing the six-membered rings into the chair confirmation greatly reduced the energies.
| Taxol Intermediate 9 (kcal/mol) | Taxol Intermediate 10(kcal/mol) | |
| Stretch | 2.6929 | 2.5492 |
| Bend | 15.8904 | 10.6672 |
| Stretch-Bend | 0.4037 | 0.3229 |
| Torsion | 18.1128 | 19.6329 |
| Non 1,4 VDW | -0.9966 | -1.2575 |
| 1,4 VDW | 12.6321 | 12.5517 |
| Dipole/Dipole | 0.1475 | -0.1822 |
| Total Energies | 48.8878 | 44.2841 |
| Models |
From these energies we can determine that intermediate 10 is the more stable isomer and the thermodynamically favoured one.
Looking at the individual energy components, it would seem the ‘bending’ energy is the greatest contributor. As the case with cyclopentadiene, this energy represents the strain on the system as a result of the deviation from the ideal conformation. This means that bonds in intermediate (9) are more strained that that in intermediate (10) indicating that the strain is due to the change in geometry of the carbonyl group/position of oxygen.
According to the literature, the hydrogenation of intermediate 10 proceeds very slowly. It is known as a ‘hyper stable’ alkene. To illustrate the reason behind the slow reaction of intermediate 10, a model of the hydrogenated product has drawn on ChemBio3D and the MM2 force field used to minimize the energy.
| Hydrogenated Product (kcal/mol) | Taxol Intermediate 10(kcal/mol) | |
| Stretch | 2.8116 | 2.5492 |
| Bend | 13.5576 | 10.6672 |
| Stretch-Bend | 0.6545 | 0.3229 |
| Torsion | 21.9969 | 19.6329 |
| Non 1,4 VDW | -1.3881 | -1.2575 |
| 1,4 VDW | 15.4102 | 12.5517 |
| Dipole/Dipole | 0.000 | -0.1822 |
| Total Energies | 53.0427 | 44.2841 |
| Models |
The hydrogenation of the alkene results in a higher total energy that that of Taxol (10), the reactant. The removal of the double bond essentially destabilized the molecule and tt is therefore not thermodynamically favourable for the reaction to proceed and as a result takes a long time.
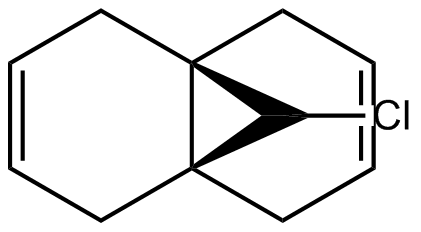
Section 4- Regioselective Addition of Dichlorocarbene
In this section, we will be looking at the 2 carbon-carbon double bonds in compound 12 and determine how prone they are to electrophilic attack and the reason behind it.
As usual, using ChemBio 3D the molecule was modelled, and geometry optimized using both the MM2 and MOPAC (PM6) fields.
| MM2 minimization (kcal/mol) | MOPAC (PM6) (kcal/mol) | |
| 17.8959 | 19.73995 |
From the literature we know that the double bond anti to chlorine is the one most prone to hydrogenation. The PM6 function was used to calculate the molecular orbitals to help explain the selectivity of the double bond anti the C-Cl.
| HOMO |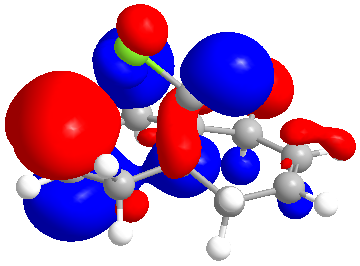 
|
| HOMO+1 |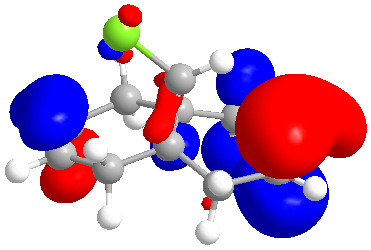 
|
| LUMO |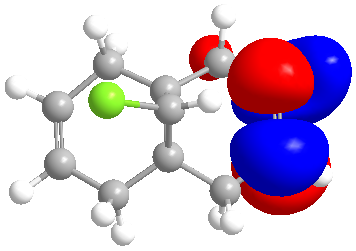 
|
| LUMO +1 |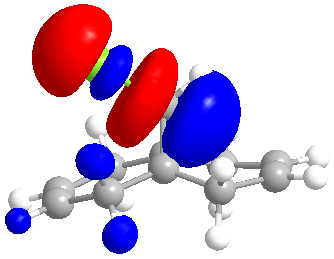 
|
| LUMO +2 |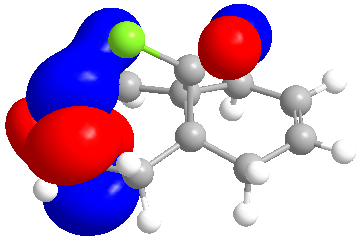 
|
| Compound 12 | Hydrogenated Compound 12 |
IR Spectrum |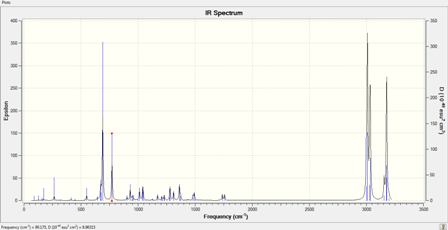
IR Spectrum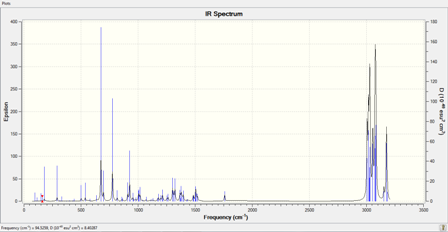 
|
| C=C Anti
|
C-C Anti
|
C=C Syn  |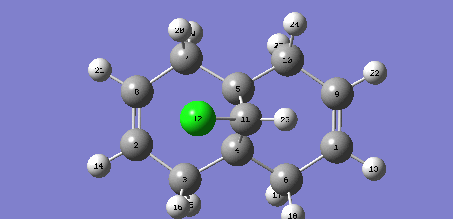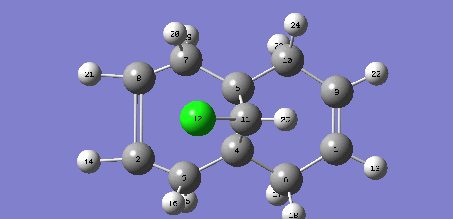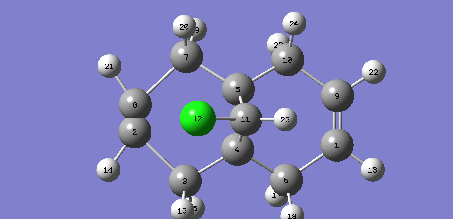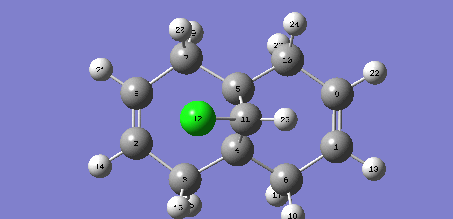
C=C Syn 
|
C-Cl  |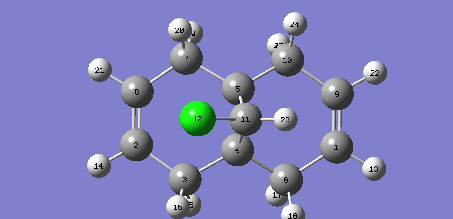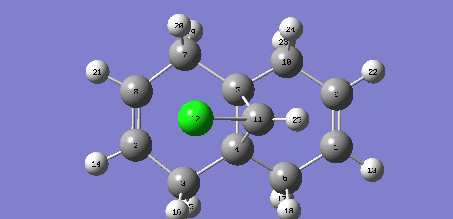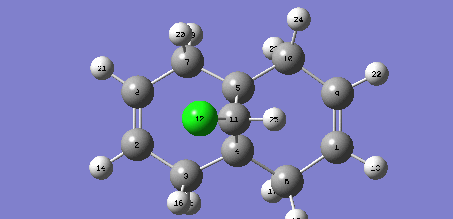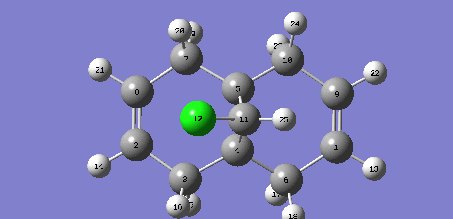
C-Cl 
|
The molecular orbitals indicate the areas of high electron density (HOMO) showing that the syn alkene is less likely to be hydrogenated.
Section 5- Structure based Mini project using DFT-based Molecular orbital methods
NMR Studies of Geometric Isomers of 3-Dehydro-β-ionone
Rhodopsin is a pigment of the retina that is responsible for the formation of the photoreceptor cells and in the perception of light.(SUB) Interest in this structure of rhodopsin, lead to the studies towards the structural properties of retinal and their lower homologues.
This project will focus on distinguishing two geometric isomers of 3-deyhdro-β-ionone, β-ionone lower homologues, using 13C NMR.
Firstly, the two geometric isomers were modelled on ChemBio3D and their energies minimized using the MM2 force field. These now refined models were then sent to a super computer for further geometry optimization. The resulting output was then edited slightly and submitted to the super computer for NMR calculations.
| Trans Isomer(2t) | Cis Isomer (2c) |
| Total Energy: 47.3857 kcal/mol | Total Energy: 23.5512 kcal/mol |
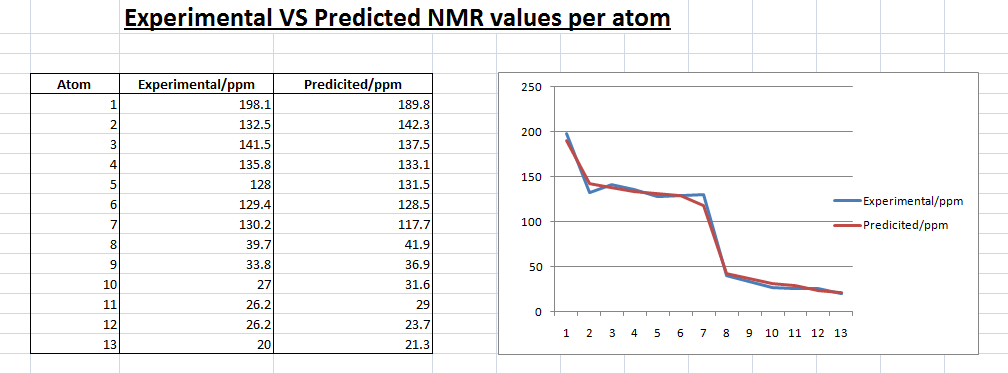
Trans Isomer 13C NMR (predicted)-
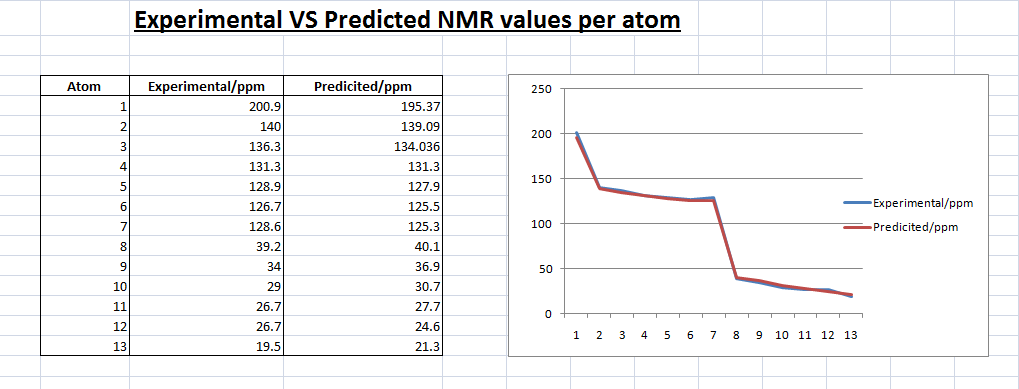
Cis Isomer 13C NMR (predicted)-
From the illustrations above, we can see that the predicted trans isomer is not as good a fit as the predicted cis isomer. The line graph above shows that there are a number of discrepancies between the predicted trans NMR values and the experimental.
This could be due the higher energy of the molecule. Looking at the energies of the two isomer after the MM2 minimization, the trans isomer has twice the total energy of the cis isomer. This could mean that the minimization was not ‘enough’ or rather the geometry of the molecule was not at it’s optimum leading to the discrepancies in the results.
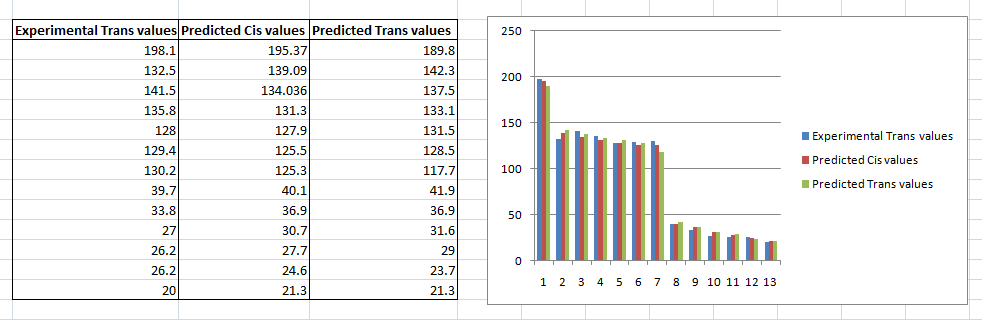
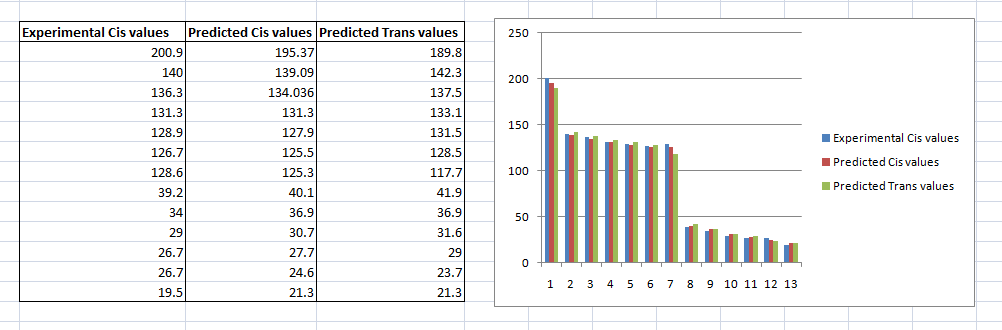
To confirm our choice of the trans and cis isomers, the images below compare the predicted cis and trans energies with the each of the experimental values.
Although, the observed difference on the bar chart is small, it is more significant on the NMR spectra. This concludes that our choice in the trans and cis isomer via NMR calculations math the experimental results.
References
1. J. Clayden, N. Greeves, S. Warren, P. Wothers, Organic Chemistry, Oxford University Press, 2006, Pages 907-913
2. A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838. DOI:10.1021/jo00356a016