Mod 3- The Transition State

Here the Schrodinger equation is solved numerically using molecular orbital based method for the Transition state of large molecule. And the the TS are located using the shape of potential energy surface.

The Cope Rearrangement Tutorial

a) The anti form of 1,5- hexadiene is created and optimsed with (HF/3-21G) using Gaussian.

The energy for this structure is -231.69253506 a.u.

The point group is Ci

b) A 1,5-hexadiene with a gauche linkage is optimised like in part a (HF/3-21G), This form should be higher in energy than the anti form as the steric is less as the C=C are on both sides of the C-C bond, this make them further apart from each other.

The energy for this structure is -231.69166702 a.u.

The point group is C1

Although it the gauche form is predicted to be higher in energy this is not true for this optimisation (5kcal/mol), this might due to the terminal C=C pi interaction. Or the method and basis set used is not accurate enough.

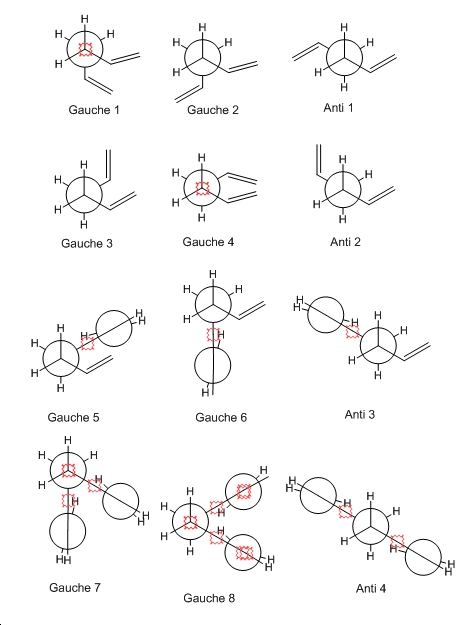
c) All possible form of the molecule is drawn below and optimised to determin which has the lowest energy.

Summeries of Different Structure Thier Point Group and Energies
Comformer	Point Group	Energy (a.u.) HF/3-21G	Relative Energy (Kcal/mol)
Gauche 1	C1	-231.69266122	3.1
Gauche 2	C2	-231.69153035	2.3
Gauche 3	C1	-231.69266122	3.1
Gauche 4	C2	-231.69166720	2.4
Gauche 5	C1	-231.68961576	1.1
Gaiche 6	C1	-231.68961575	1.1
Gaiche 7	C2	-231.68771616	0
Gaiche 8	C2	-231.68771615	0
Anti 1	Ci	-231.69253530	3.0
Anti 2	C2	-231.69260236	1.7
Anti 3	C1	-231.69097055	2.0
Anti 4	C2h	-231.68907066	0.8

d) All of the different forms optimised can be identified in appendix 1 with the same point group and similar energy. On my table there there are 2 pair of enantiomer of the gauche form.

e) The anti molecule optimised in part a) is the one with Ci point group.

f) Differnt method and basis set is compared here to compare the effect it make to the calculation and the structure.

Table of Comperison Between the Two Different Methods
Dihedral Angel(°)	HF/3-21G	B3LYP/6-31G

Energy (a.u.)	-231.69253506	-234.55971534
C(14)-C(7)-C(4)	124.802	125.215
C(4)-C(1)-C(9)	111.362	112.648
C(7)-C(4)-C(1)	111.362	112.648
C(1)-C(9)-C(11)	124.802	125.215
H(15)-C(14)-H(16)	116.319	116.292
H(15)-C(4)-H(6)	107.699	106.703
H(2)-C(1)-H(3)	107.699	106.703
H(13)-C(11)-H(12)	116.319	116.292
Bond Distance(A)	HF/3-21G	B3LYP/6-31G
C(14)-C(7)	1.31627	1.33825
C(7)-C(4)	1.50908	1.50709
C(4)-C(1)	1.55272	1.55509
C(9)-C(1)	1.50908	1.50709
C(11)-C(9)	1.31627	1.33825
C(11)-H(13)	1.07336	1.08596
C(11)-H(12)	1.07446	1.08782
C(9)-H(10)	1.07694	1.09170
C(1)-H(2)	1.08556	1.10030
C(1)-H(3)	1.08478	1.09857
C(4)-H(5)	1.08478	1.09857
C(4)-H(6)	1.08556	1.10030
C(7)-H(8)	1.07694	1.09170
C(14)-H(15)	1.07466	1.08782
C(14)-H(16)	1.07336	1.08596

The overall structure is the same(only small flatuations of bond length and dihedral angles for around 0.2A or 1degree) The struture optimsed using B3LYP/6-31G is more symmetric with slight longer bonds and wider angles.

g) A frequency calculation is carried out to obtain the finnal energy with additinal term to compare.

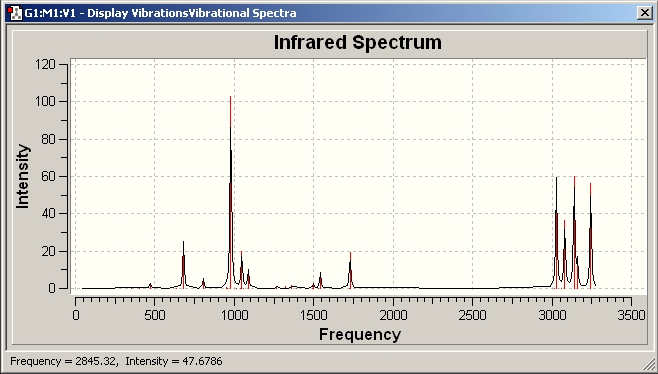
IR spectrum for Ci Anti-conformoner

Additional terms can be obtained.

Sum of electronic and zero-point Energies=           -234.416226

This is the PE at 0 K with zero pt vibrational energy

Sum of electronic and thermal Energies=              -234.408944

Energy at 298.15 K and 1 atm with contribution of rotational vibrational and translational energy

Sum of electronic and thermal Enthalpies=            -234.407999

This includes the correction for RT ( H=E+RT) improtant for dissociation reaction

Sum of electronic and thermal Free Energies=         -234.447807

this includes the entropic contribution to free energy (G=H-TS)

Literature

Brandon G. Rocque, Hason M. Gonzales and Henry F. Schaefer III , Molecular Physics, "2002", Vol. 100, 'No. 4', 441-446 DOI:10.1080/00268970110081412 2 10.1080/00268970110081412

"Boat" and "Chair" Transition Structure

In this section three different methods are used to optimise a transition structure

1. compute force constants on the beginning of calculation

2. Redundant coordinate editor is used

3. the QST2

a) a CH2CHCH2 fragment is drawn and optimised with HG/3-21G, 2 of this fragment is then used to create a transition state with the chair conformation with each end of the fragments are 2.2 Å apart

b) If the guessed transition state molecule has a reasonable geometry, it can be optimised by producing the -ve direction of the curvature and to compute its Hessian of the 1st step of opimisation.

The Hartee Fock method is used to optimised the chair TS created in part a) and its geometry is checked with the one in Appendix 2

An imaginary frequency of -818.045cm-1 is produced

c) When the case that the guess structure does not quite match the actual geometry. Another method can be used to optimise the molecule, this is to freeze the reacting coordinate and minimise the rest of the molecule. After the molecule is relaxed, the reacting coorinate is 'un-frozen' and is optimised again.

The same guess structure is optimised using this method with 2 terminal C frozen.

[[image:]]

The 2 different method gives very similar structure although the bond distances is fixed to 2.2 Å for C)

d)

Comparison of the optimised structures by Computing Force Constants at the Beginning and by Using Redundant Coordinate Editor
	Optimised Structure by Computing Force Constants at the Beginning	Optimised Structure Using Redundant Coordinate Editor

Bond Lengths of Breaking/Forming Bond (A)	2.02048,2.02028	1.55018, 4.39000

The two different TS optimisted by the two different method is quite differnt however the one optimised using the redundant coordinated method has optitmised to be very similar to the Gauche conformation of 1,5-hexadiene(C2 point group)

the bond forming/breaking lengths are quite different too, for the redundant corrdinate method is much longer (about 3 times)

e) Using the QST2 method has a lot of advantage, one of it is it's completely automated, and it can specify the product and reactants

Here the optimised Ci Anti 1,5-hexadiene is used, first the labelling of the molecule is changed so the product can corresponds to the reactant.

Than is it run with the QST2 method howere the job will fail.

It failed as the calculation method fail to locate the boat structure from reatant to product as it only interpolated between them linearly. ( not considering to rotate the allyl fragment around the central bond)

Therefore the geometry of the product and reactant has to be modified to be closer to the boat structure like below

f) From the previous exercise it is noticed that the boat conformation is similar to the Ci Anti conformer of 1,5-hexadiene while the chair TS is close to the C2 Gauche conformer of 1,5-hexadiene.

It cannot predict the reaction paths will lead to which conformer though

The IRC method takees small geometry stops to create a series of points with the gradient of when energy surface is steepest. Only the forward reaction direction is computed as the reaction coordinates are symmetrical. (force constant=once, no of pt= 50).

3 methods can be used to improve the calculation.

i) a normal minisation is ran using the last point on the IRC

ii) Specify a larger no of pt and restart IRC

iii) Run the IRC and specify that force constants is computed every step. (most accurate by most expensive and sometimes don't work on larger system)

The three approach is compared below.

Comparison of the Three Differnt Approach
Approach 1	Approach 2 (100 pts)	Approach 2 (150 pts)	Approach 3

looks like the TS in the redundant coordinated method meaning the guess structure is not accurate enough	minimum is still not reached when the number of pt is increased to 100	so it is increase to 150, this time much longer time is needed to calculated, it looka like the TS as too many pts are used and the calc veers off to the wrong direction	longer time is needeed to run this but it is cloest to reality

g)

Boat and Chair Optimised by B3LYP/6-31G
	Chair conformation	Boat Conformation
Geometry
Energy (a.u.)	-234.55863028	-234.55927375

The Energy difference for both the Guache and Anti conformor for both calculation is about 1800kcal/mol

Literature

Shogo Sakai, International Journal of Quantum Chemistry, "2000", Vol. 80, 1099–1106DOI:1099::AID-QUA59

Mini Project

In this Project we will look at the Diels Alder Cycloaddition, which is a type of pericyclic reaction. There is no intermediate form during this reaction as the bonds will be form/break in a concerted cyclic transition state. Wether the reaction is allowed or forbidden will be decided on the number of π orbital involved. Belows are a few rule

The reaction can only occur when the HOMO can interact with the LUMO. For the HOMO and LUMO to interact a significant overlapping between the orbitals are needed, so they need to be in the same symmetry.

Sometimes the dieneophine will have substituents with π bonds, these can interact with the product and stabilising the reaction.

For this reaction we are going to investigale it is a 4s +2s reaction as there are 4π from the butadiene and 2π from ethylene and the π orbital can be either a(asymmetric) or s (symmetric).

The LUMO of butadiene and HOMO of ethylene are s while the HOMO of butadiene and LUMO of ethylene are a. The same symmetry makes interaction possible between the HOMO and the LUMO.

i)The Reactant Molecule: Cis-butadiene

a cis-butadiene is created and optimised with HF/3-32G

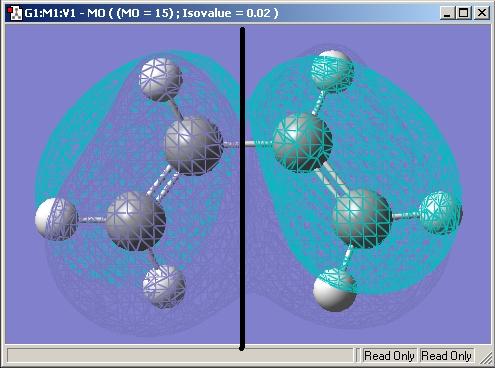
it's MO is then produced and the HOMO and LUMO is shown

HOMO : asymmetric

LUMO : symmetric

The LUMO is s and comfrims with the explanation above

ii)The Ethylene-Cis-butadiene Transition state

This TS has an envolopestructure that maximising the ethylene π orbital and π orbitals of butadiene overlapping. It is found from the lit that the interfragment distances is about 2.201Å.

The reaction coordinate is created using computed force constant matrix of the 1st step of the optimisation

Optimised structure of the Ethylene cis Butadiene TS
Bond	Bond Length (A)
C4=C3	1.36746
C2=C1	1.36747
C3-C2	1.39615
C13=C11	1.22386
C13--C4	2.19993
C11--C1	2.20005
Bond	Bond Angel (degree)
C4-C3-C2	121.585
C1-C2-C3	121.630
C11-C13-C4	111.407
C3-C11-C1	111.399
C13-C4-C3	100.701
C11-C1-C2	100.674

Frequency

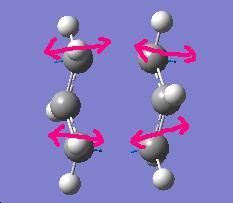
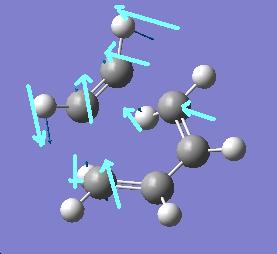
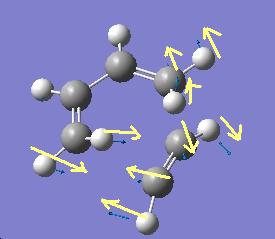
There is one negative frequency at -838.924cm-1 with the motion shown below

the lowest positive freqency is at 268.156cm-2 and the motion is shown below

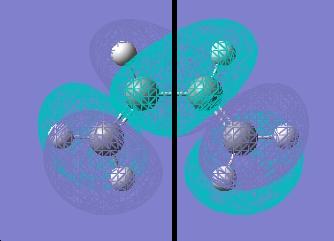
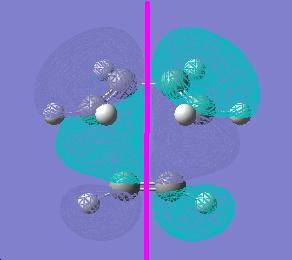
the MO diagram of ethylene-cis-butadiene for the HOMO and LUMO is shown below

HOMO: asymmetric (a)

LUMO: symmetric (s)

Literature

1. Shogo Sakai, J. Phys. Chem. A, "2000", 104 (5), 922-927 DOI:10.1021/jp9926894

2. Joey W. Storer, Laura Raimondi and K. N. Houk, J. Am. Chem. Soc., "1994", 116 (21), 9675-9683 DOI:10.1021/ja00100a037

3. Yi Li, and K. N. Houk, J. Am. Chem. Soc., "1993", 115 (16), 7478-7485 DOI:10.1021/ja00069a055

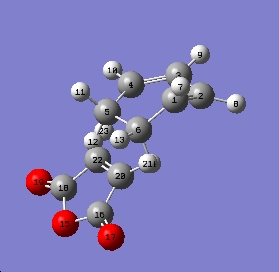
iii) The Cyclohexa-1,3-diene reaction with Maleic Anhydride

Maleic anhydride and cyclohexa-1,3-diene undergo facile Diels-Alder to give a endo product. This is the kinetic prouct as the exo TS has high energy. Here the regioselectivity is studied

The endo and exo structure are optimised and thier structure is optimised and studied. A guess structure is 1st created, as the guess structure is quite inaccurate it is optimised by freezing the reaction co-ordinate and then the rest of the molecule will be minised, after this the reacting coordinate is unfrozen and fully relaxed and is optimised again.

Optimised endo TS

Table with Otpimised Bond Lengths in the Endo TS
Bond	Bond Length (A)
C4..C20	1.54725
C1..C22	1.54000
C6-C5	1.53184
C2-C3	1.550425
C3=C4	1.54011
C1=C2	1.54202
C22=C20	1.53268
C22-C18	1.51702
C20-C16	1.51604
C18-O15	1.38328
C16-C15	1.39284
C18=O19	1.89283
C16=O17	1.89328

Optimised exo TS

Table with Otpimised Bond Lengths in the exo TS
Bond	Bond Length (A)
C1..C20	1.54726
C4..C22	1.54090
C6-C5	1.55127
C2-C3	1.56034
C3=C4	1.54341
C1=C2	1.54212
C22=C20	1.53227
C22-C18	1.51969
C20-C16	1.51958
C18-O15	1.38953
C16-C15	1.39661
C18=O19	1.89732
C16=O17	1.89732

Both TS has similar bond lengthes

Transtion state energies (a.u.)

Endo = -606.90823898 Exo = -606.90823902

The exo have slighly higner energy so the endo is slightly more thermodynamically stable

MO diagram

Endo HOMO

Asymmetric

Endo LUMO

Asymmetric

Exo HOMO

Asymmetric

Endo LUMO

Asymmetric

The endo form is decided to be thernodynamically more stable as the bonding interaction secondary orbital interaction from the C=O groups interacts with the C=C of the cis butadiene and create a good overlap. This is abscense in the Exo case as they are not in the same orientation.