Rep:Mod:felicmod2
Introduction
By using the Gaussian programme, the structure and bonding of molecules can be investigaed by the graphical interpertation given by the Gaussian.
Optimising Molecule
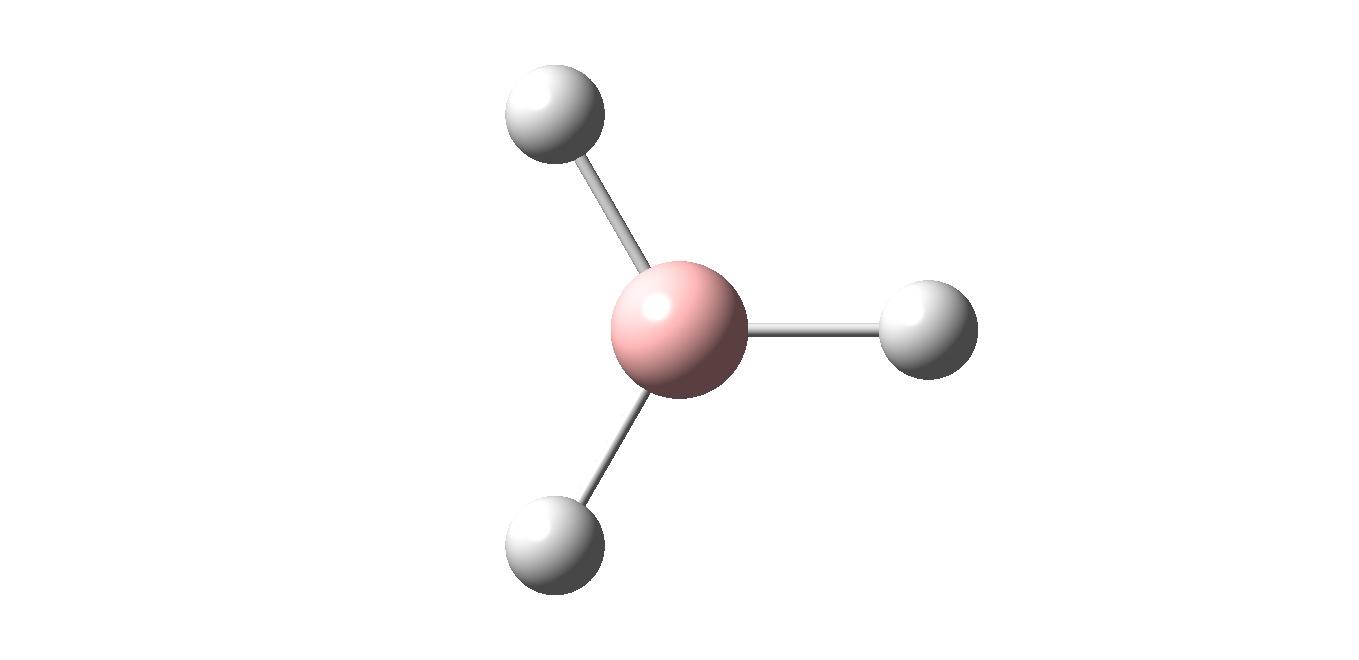
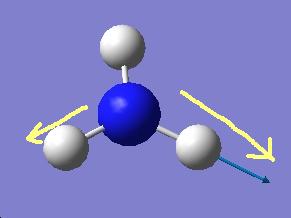
BH3
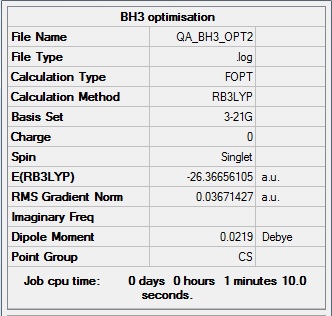
A small molecule ( BH3) is investigaed as a practice molecule. It is optimised by Gussian with the B3LYP method and the basis set of 3-21G.
Method: Methods such as B3LYP in this case is approoximations that are made while we try to solve the Schrodinger equation.
Basis Set: Determines the no of fuctions when describing the electronic structre and therefore affect the accuracy increase accuracy: 3-21G<6-31G<6-31+G
In this case the BH3 molecule is not optimised with a very high accuracy but this make the time needed for the calculation very small
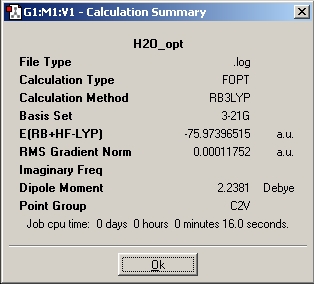
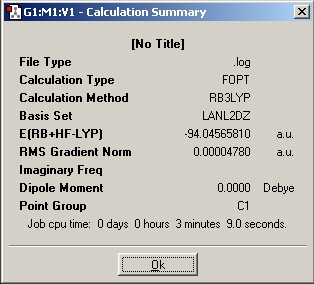
After the optimisation information about the bond length and angle can be determined
Optimised
B-H bond distance : 1.19435A
H-B-H bond angle : 120.00 degree
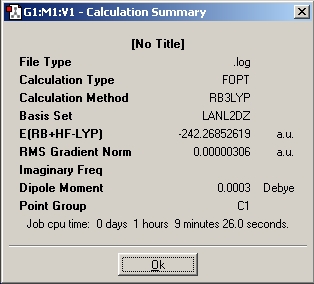
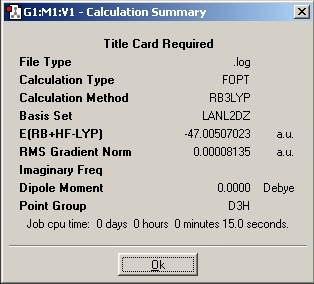
A summary of the calculation can be obtained which the improtatant info of the caluclation:
Optimisation plot
this shows the energy and the gradient of energy at each optimisation step with the corresponding structure.
Total Energy Curve
This give the potential energy surface and to serac for the monimun of that enregy surface
There is no bond shown on the BH3 molecule at the 1st optimisation step as the bond length has exceeded the pre-defined value in Gaussian.
The Final optimised structure of the molecule has the smallest gradient and most negative energy.
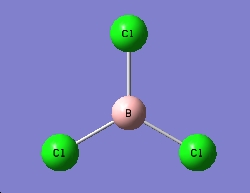
BCl3
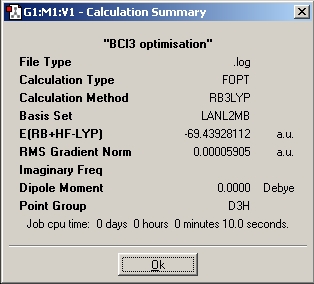
As BCl3 is a much bigger molecule than BH3 with a second row element, a large basis set and pseudo potentials have to be introduce to reduce the compitatatioanl effort. Cl has 17 electrons, but it is only the valence electrons that determintes the chemical proterties and the bonding interactions, therefore the concept of a pseudo-potential can be introduced, this will not effect a lot of the accuracy but will signgificantly reduce the calculation time neede. A lager basis set is needed to improve the accuracy. Although the higher the basis set is the more accuracte the calculation is going to be, but this will take a much longer time, a balance is needed between accuracy and the calculation time. In this case of BCl3, the basis set of LanL2MB is used and the result is as followed.
Optimised
B-Cl bond distance : 1.86592A
Cl-B-Cl bond angle : 120.00 degree
Small Molecule H20
H2O is chosen to be optimised and it is deposited in the Chemical SCAN database. Below are the results
the xyz coordinates.
Center Atomic Atomic Coordinates (Angstroms) Number Number Type X Y Z --------------------------------------------------------------------- 1 8 0 0.000000 0.000000 0.110812 2 1 0 0.000000 0.783976 -0.443248 3 1 0 0.000000 -0.783976 -0.443248 ---------------------------------------------------------------------
Optimised
O-H bond distance : 0.99683A
H-O-H bond angle : 103.991 degree
A longer time is needed for this calculations as expected as this is a larger molecule with a larger basis set.
As D-space does not accpet my file, I have upload it to here
https://www.ch.ic.ac.uk/wiki/index.php/Image:H2o_log_12713.out
Vibrational Analysis/Animating Vibrations
While the 1st derivative define the slope, the 2nd derivative define the curvature of the function. When it is +ve, a minimum is given while a maximum is gain when the value is -ve.
The 2nd derivative of the PE surface gives the frequency analysis. In this case, a minimum will occur when all the frequencies are +ve, a trasition state when one of the freqencies is -ve and if more than one of them is -ve the optimisation has failed.
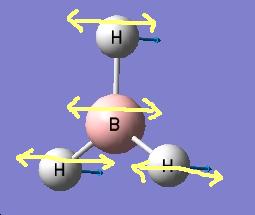
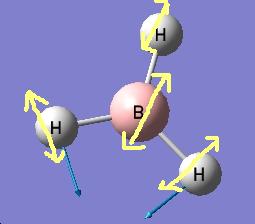
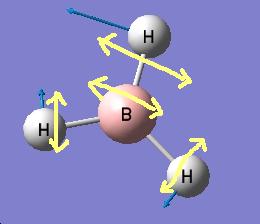
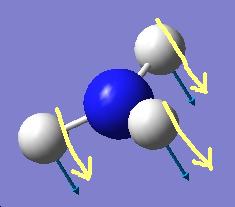
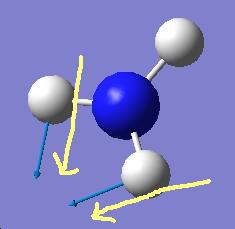
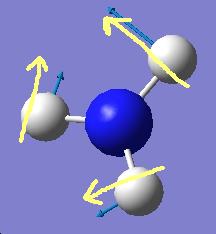
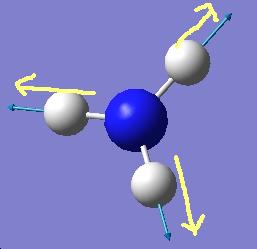
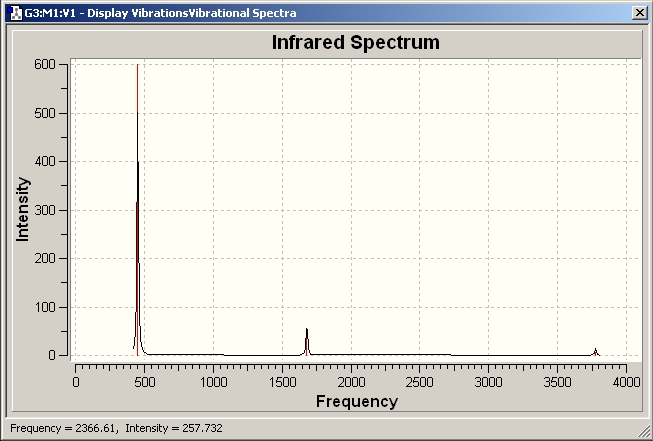
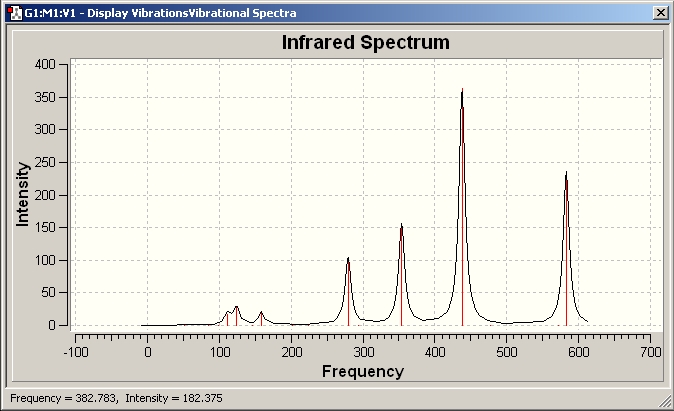
The frequency analysis we have done in this case show a fully optimised structure of BH3 and therefore confimed a sucessful optimisation is preformed.
| No | Form of Vibration | Frequency | Intensity | Symmetry of D3h Point Group |
|---|---|---|---|---|
| 1 | 
|
1145.72 | 92.6991 | A2 |
| 2 | 
|
1204.66 | 12.3789 | E' |
| 3 | 
|
1204.66 | 12.3814 | E' |
| 4 | 
|
2592.79 | 0 | A'1 |
| 5 | 
|
2731.31 | 103.837 | E |
| 6 | 
|
2731.31 | 103.83 | E |
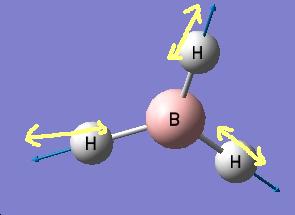
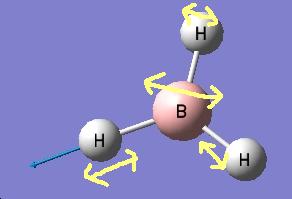
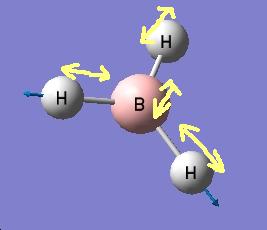
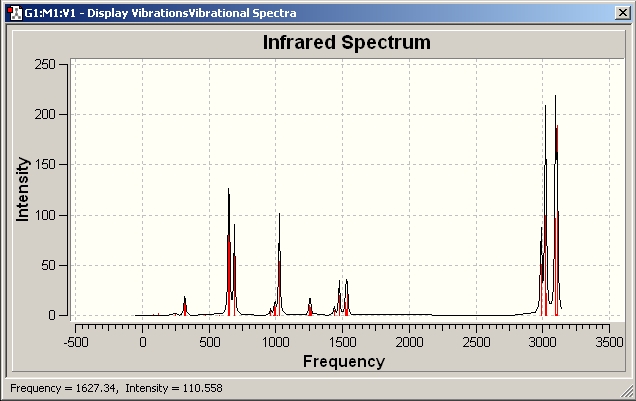
The results show 2 pair of vibrations with the same frequency and intensity and they correspond to the doubly degenerated orbitals E' and E"
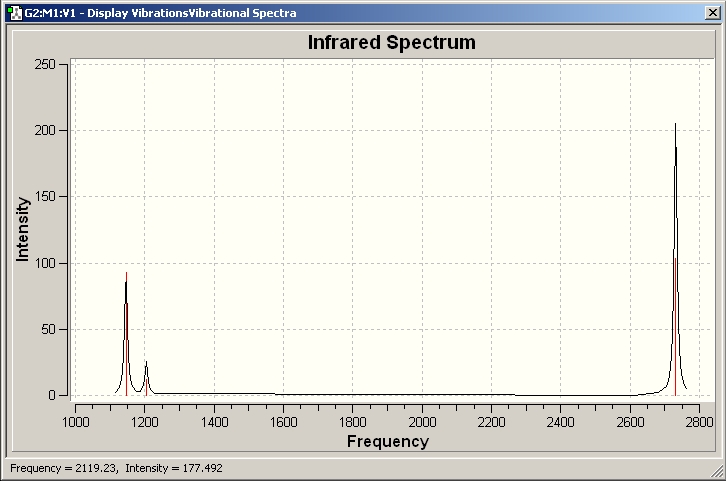
BH3 IR spectrum
Although there are 6 vibration mode there are only 3 peaks observed, this is due to the double degeneracy of the orbitals with the same frequency and intensity, so only one peak is observed
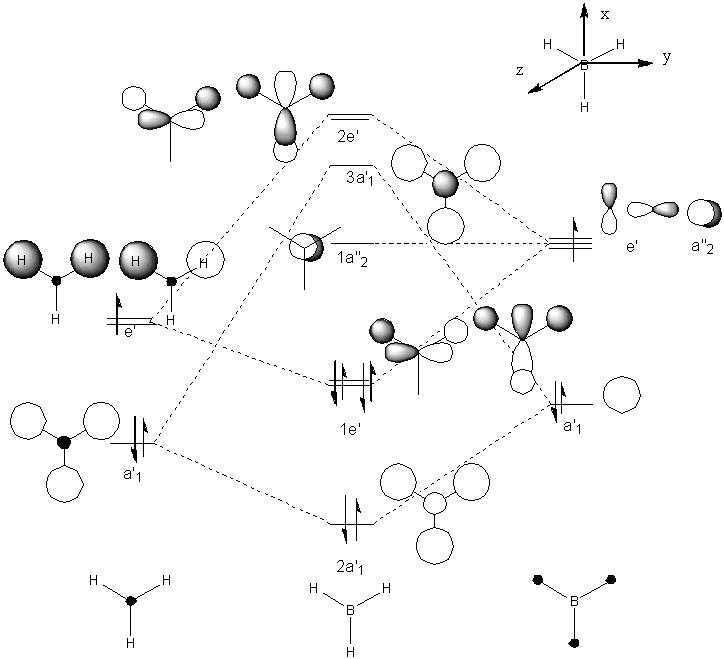
Molecular Orbitals
The computed MO and the quantitative ones are compared below.
The qualitative MOs are shown in the MO diagram below
| Predicted Qualitative MO | Qualitative MO | |
|---|---|---|
| LUMO+3 |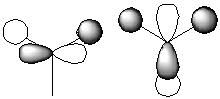 
|
 
|
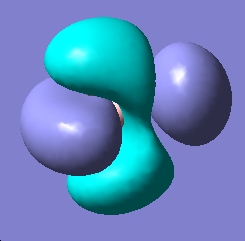
| LUMO+2 | 
|
|
| LUMO+1 | 
|
|
| LUMO | 
|
 
|
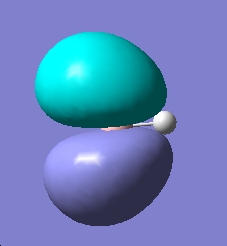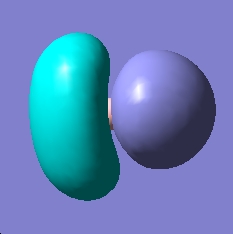
| HOMO - degenerate | 
|
|
| HOMO-1 | 
|
|
They appear to be very simiar, this can show that the predicted MO theory is quite accurate while the qualitative MO will be the most acccurate.
Isomers of Mo(CO)4L2
Thermal stabilities of the cis and trans isomer of Mo(CO)4L2 where L=P(Me)3 are predict by a series of calculation as this is a large molecule.
The 1st step is to optimise the rough geometry with the method of B3LYP and basis set of LanL2MB, this is a low basis set and loose convergence is set, this is because if the normal convergence is used the limit will never be reached and the calculation will not converge.
1. B3LYP/LanL2MB
Unique identifier for cis-Mo(CO)4L2
As D-space does not accpet my file, I have uploaded it to here
https://www.ch.ic.ac.uk/wiki/index.php/Image:Cis_log_12794.out
Unique identifier for trans-Mo(CO)4L2
As D-space does not accpet my file, I have uploaded it to here
https://www.ch.ic.ac.uk/wiki/index.php/Image:Trans_log_12792.out
The 2nd step is to perform optimisation again using the method of B3LYP and a different basis set of LanL2DZ, this is a high basis set and a pseudo-potential option. Normal convergence criteria is used.
2. B3LYP/LanL2DZ
Unique identifier for cis-Mo(CO)4L2 10042/to-1753
Unique identifier for trans-Mo(CO)4L2
10042/to-1694
The 3rd and final step is to compte the IR frequencies of both of the isomer.
3. IR
Unique identifier for cis-Mo(CO)4L2
10042/to-1755
Unique identifier for trans-Mo(CO)4L2
10042/to-1745
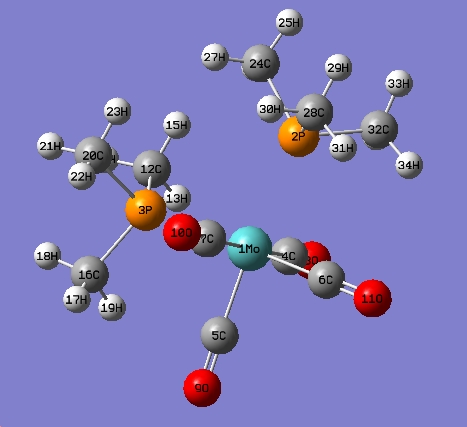
cis-Mo(CO)4L2
The optimised structure is shown below
There is no P-Mo bond shown as the bond distance has exceed the pre-defined value in GaussView.
| Bond | Optimised Bond Length (A) | Experimental Bond Length (A) |
|---|---|---|
| Mo-P(2) | 2.4807 | 2.533 |
| Mo-P(3) | 2.65193 | 2.525 |
| Mo-C(7) | 2.03243 | 1.997 |
| Mo-C(5) | 1.98297 | 1.981 |
| Mo-C(4) | 2.03251 | 2.304 |
| Mo-C(6) | 1.98101 | 1.983 |
| C(7)-O(10) | 1.18794 | 1.150 |
| C(5)-O(9) | 1.19128 | 1.163 |
| C(4)-O(8) | 1.18797 | 1.150 |
| C(6)-O(11) | 1.19237 | 1.125 |
| P(2)-C(24) | 1.89565 | 1.836 |
| P(2)-C(28) | 1.89038 | 1.863 |
| P(2)-C(32) | 1.89039 | 1.815 |
| P(3)-C(12) | 1.89284 | 1.819 |
| P(3)-C(16) | 1.88995 | 1.837 |
| P(3)-C(20) | 1.89294 | 1.862 |
| Bond | Optimised Bond Length (°) | Experimental Bond Length (°) |
|---|---|---|
| P(3)-Mo-P(2) | 95.317 | 94.75 |
| C(7)-Mo-P(2) | 89.879 | 87.8 |
| C(5)-Mo-P(2) | 175.168 | 176.3 |
| C(4)-Mo-P(2) | 89.520 | 89.7 |
| C(6)-Mo-P(2) | 86.234 | 94.0 |
| C(7)-Mo-P(3) | 88.655 | 87.8 |
| C(5)-Mo-P(3) | 89.512 | 89.3 |
| C(4)-Mo-P(3) | 89.919 | 87.1 |
| C(6)-Mo-P(3) | 178.442 | 175.5 |
| C(7)-Mo-C(5) | 90.387 | 89.9 |
| C(7)-Mo-C(4) | 177.463 | 177.0 |
| C(7)-Mo-C(6) | 91.201 | 89.2 |
| C(5)-Mo-C(4) | 90.422 | 92.9 |
| C(5)-Mo-C(6) | 88.937 | 88.4 |
| C(4)-Mo-C(6) | 91.246 | 89.9 |
| Mo-C(7)-O(10) | 179.325 | 178.0 |
| Mo-C(5)-O(9) | 178.835 | 179.1 |
| Mo-C(4)-O(8) | 179.376 | 178.5 |
| Mo-C(6)-O(11) | 179.791 | 178.0 |
From the data it can be shown that the experimental and the optimised structure after the calculation is very similar apart from some of the C-Mo-P angel and P-C bond length as different ligand were used in the reference.
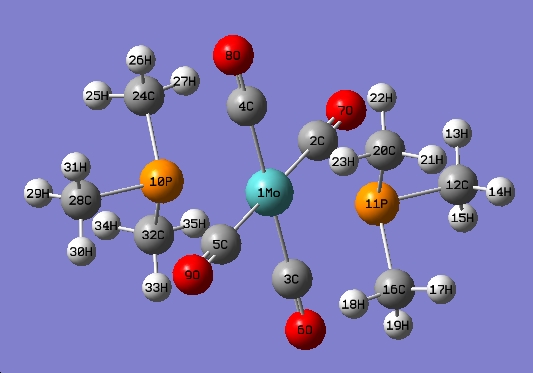
trans-Mo(CO)4L2
The optimised structure is shown below
The P-Mo bond is not shown here due to the same reason as before.
| Bond | Optimised Bond Length (A) | Experimental Bond Length (A) |
|---|---|---|
| Mo-P(10) | 2.4807 | 2.57171 |
| Mo-C(4) | 2.02852 | 2.024 |
| Mo-C(2) | 2.02854 | 2.035 |
| C(4)-O(8) | 1.18794 | 1.18982 |
| C(2)-O(7) | 1.18981 | 1.135 |
| P(10)-C(24) | 1.188985 | 1.840 |
| P(10)-C(28) | 1.88945 | 1.826 |
| Bond | Optimised Bond Length (°) | Experimental Bond Length (°) |
|---|---|---|
| C(4)-Mo-P(10) | 89.879 | 89.004 |
| C(3)-Mo-P(10) | 90.995 | 88.34 |
| Mo-C(4)-O(8) | 179.678 | 179.2 |
| Mo-C(2)-O(7) | 179.664 | 179.0 |
| Mo-P(10)-C(24) | 115.703 | 119.77 |
| Mo-P(10)-O(28) | 117.083 | 113.95 |
Again the two sets of value are very similar meaning the optimisation is completed.
The Cis vs the Trans
The Mo-P bond length of the cis isomer are longer than of the trans isomer
In the trans-isomer all the metal carbon bond have simiar length as they are all trans to each other.
AS the CO ligand are better π-acceptor than the P(Me)3 ligand, this make the Mo-C bond for the CO ligand trans to a P(Me)3 group shorter than those trans to another CO ligand. This is due to when the CO is trans to each other, they compete for the e- density of the metal and reduce the level of back bonding.
| Cis | Trnas | |
|---|---|---|
| Energy (a.u.) | -773.36023414 | -773.35731185 |
The cis isomer has sighly lower energy meaning it is slightly more stable that the trans isomer, but sterically the trans-isomer should be more stable becuse of the two bulky P(Me)3 group with the angle of 118 degree in the cis version. In this case the electronic factor is more important than the steric factor.
Methods to Alter the Relative Ordering of the Cis and Trans-isomers
According to the results, it appears that if the ligand has a larger cone angle the eqilibrium will move the the trans form due the the increasing hinderd steric. If it is intended to shift the equlibrium to the cis side, Hydrogen bonding can be interduced. There are two type: intermolecular and intramolecular. For intermolecular H-bonding can be introduced by using a ligand that is capable of H-bonding and its protonated form as another ligand, forcing they come together and to be cis to each other. For intramolecular interaction, a ligand like a protonated pyridyl ring can be introduced.
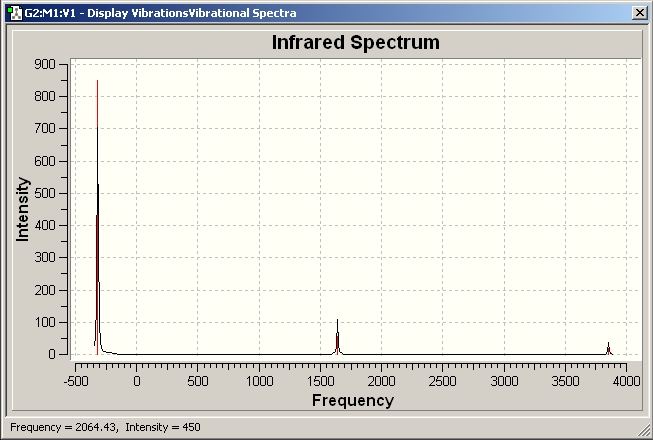
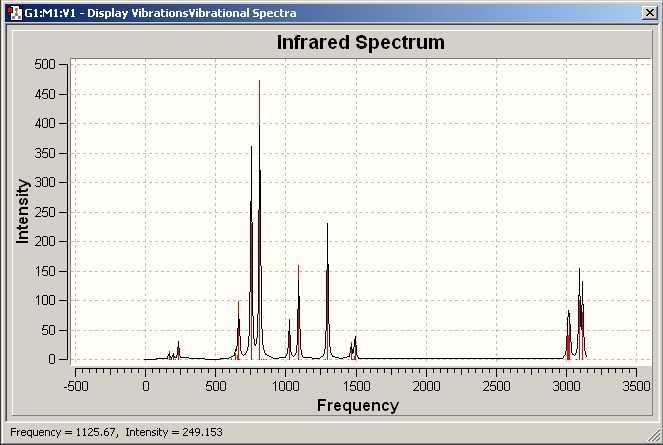
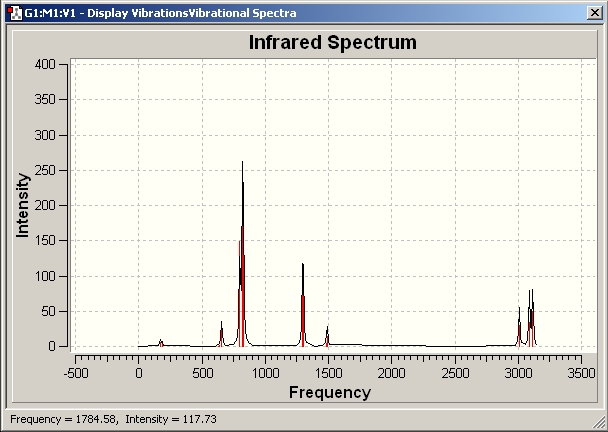
IR spectra
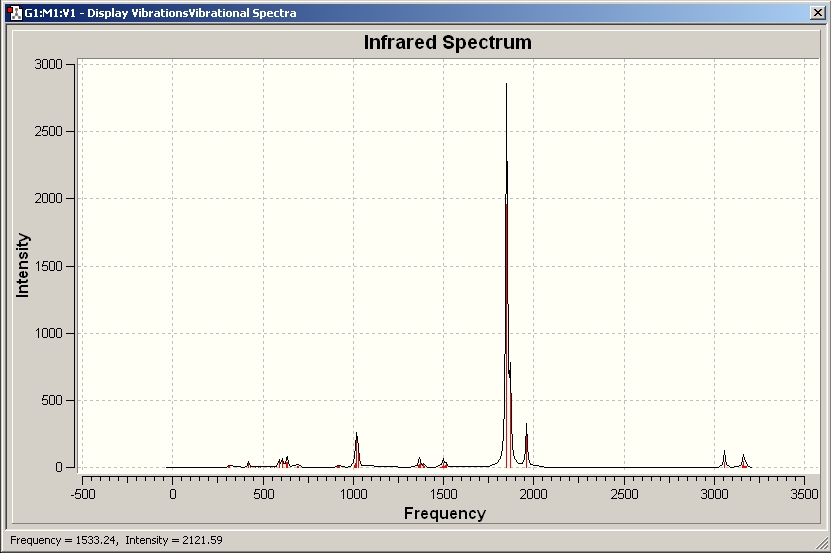
IR spectrum for the trans-isomer
It can be seen that the most intense peak is at 1840.25 due to C=O stretching and the experimental data for trans-[Mo(CO)4(PPh3)2] is ranging from 1886.05
IR spectrum for the cis-isomer
It can be seen that the most intense peak is at 1850.72 due to C=O stretching and the experimental data for cis-[Mo(CO)4(PPh3)2] is ranging from 1884.12-2013.33
The C=O stretches peak for the PPh3 ligand are larger than for the Me ligand as the methyl group is a better electron donaor, there is a bigger level of back-bonding between the C=O π* from the Metal d-orbital.
References
1. Dennis W. Bennett, Tasneem A. Siddiquee, Daniel T. Haworth, Shariff E. Kabir and Farzana Camellia, J. Chem. Cryst., '2004', "24", 6, 353-359 DOI:10.1023/B:JOCC.0000028667.12964.28
2. Gary M. Gray and Yalin Zhang, Journal of Chemical Crystallography, '1993', "23", 9 DOI:10.1007/BF01187272
3. Leeni Hirsivaara, Matti Haukka and Jouni Pursiainen, Inorg. Chem. Comm., '2000', "3", 508-510 DOI:10.1016/S1387-7003(00)00131-3
4. F. Albert. Cotton, Donald J. Darensbourg, Inorg. Chem., '1982', "21"9 (1), 294-299 DOI:10.1021/ic00131a055
Ammonia, Folliwing a Reaction Path
When the H atoms quantum tunnelling from one side of the N atom to the other it has to overcome a low potential barrier. This is the cause of the inversion doubling of the vibrational modes of ammonia
Symmetry
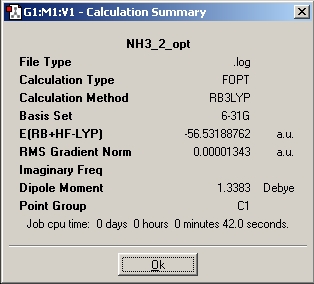
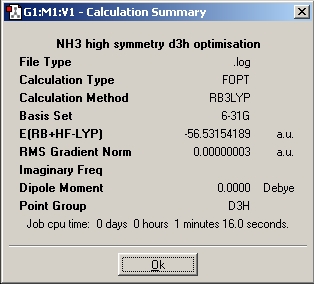
Ammonia of different symmetry is optimised using the B3LYP method of basis set of 6-31G
The three different molecule is optimised and below are the results.
| C3v | C1 | D3h | |
|---|---|---|---|
| Final Structure | 
|
|
|
| Time Needed for Optimisation | 26s | 42s | 1min 16s |
| Energy (a.u.) | -56.53188590 | -56.53188762 | -56.53154189 |
| Energy (kJ/mol) | -148424.45 | -148424.46 | -148423.55 |
The time needed to optimised the ammonia with D3h summetry has taken the longest, this means it has more symmetry element in this structure and hence need most time to solve.
After looking at the structures, it is shown that the molecule can not break symmetry during the optimisation, this mean when a highly symmetric structure is to be optimised, the best optimisation may be impossilbe to be produced.
For ammonia the structure with the lowest energy is D3h, but as the molecule is quite small the small energy difference is not significant.
Effect of Different Methods
| Groud State C3V ( high level basis set) | Transition State Planar( high level basis set) | Groud State C3v( low level basis set) | Transition State Planar( low level basis set) | |
|---|---|---|---|---|
| Method/ Basis set | 6-311G/MP2 | 6-311G/MP2 | 631G/B3LYP | 631G/B3LYP |
| Time Needed for Optimisation | 32s | 1min 37s | 26s | 1min 16s |
| Energy (a.u.) | -56.43444511 | -56.42664911 | -56.53188590 | -56.53154189 |
| Energy (kJ/mol) | -148132 | -148148 | -148424 | -148423 |
The difference of basis set 6-31G to 3-11G is quite small for the time needed for the calculation however when the method is changed from B3LYP to MP2, much more time is needed. how ever this gives a much better energy differnence of the transition and ground state. But while the expermental energy barrier for the inversion is 24.3 kJ/mol, the calculated energy is much higher ( about 10 times), this means for a more accurate optimisation an even higher method should be used.
Inversion Mechanism
Sometimes a "scan" is computed to connect the transition state and ground state. The "scan" is computed by varying one coordinate when the others are being optimised. In the case of Ammonia, the Hydrogen atomes are allowed to move down from the plane.
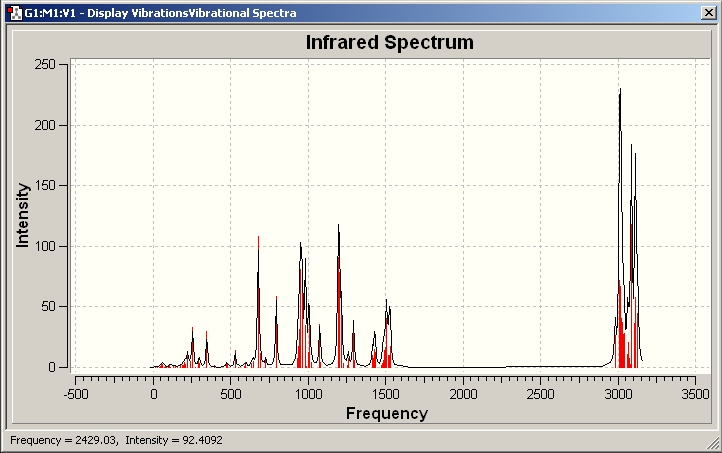
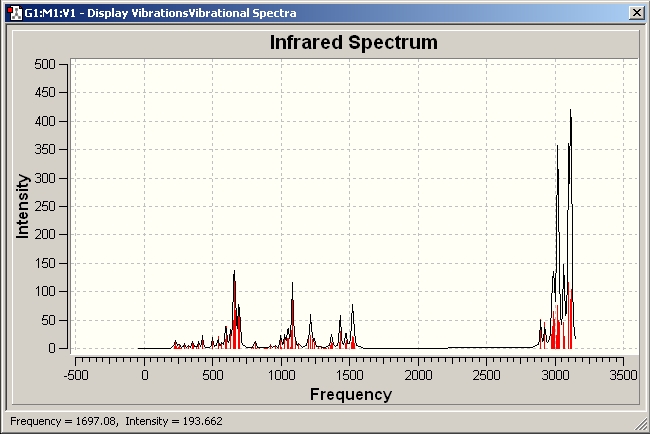
Vibrational Analysis
| Vibrational Frequencies of C3v Structure | Intensity | Vibrational Mode | Vibrational Frequencies of D3h Structure | Intensity | Vibrational Mode | |
|---|---|---|---|---|---|---|
| 1 | 452.302 | 599.472 | 
|
-318.051 | 849.113 | 
|
| 2 | 1680.47 | 41.7256 | 
|
1640.59 | 55.9828 | 
|
| 3 | 1680.47 | 41.7245 | 
|
1640.59 | 55.9805 | 
|
| 4 | 3575.43 | 0.0688 | 
|
3635.71 | 0 | 
|
| 5 | 3775.76 | 7.0892 | 
|
3854.27 | 19.5951 | 
|
| 6 | 3775.76 | 7.0884 | 
|
3854.27 | 19.5963 | 
|
Compted IR spectrum for C3v
Compted IR spectrum for D3h
They are very similar to each other.
Mini Project
Usually alkylaluminium compounds form a 3c2e methyl bridge bond to form a dimer, this bond has very distingishing features that it has a small Al-C-Al angle of approx 75 degree. But this bond is quite weak and when the alkyl group increase in size, the dissociation of trialkylaluminum compounds will be flavoured.
Here different alkylaluminium compounds with different a different size of R group will be investigated
The chosen compounds are Al2(R)6 and Al(R)3 where R=CH3, C2H5 and C3H7 respectively.
Optimisation
These molecule are optimised 1st using the method of B3LYP with the basis set of LanL2MB to get a rough approximation, then it is optimised again using the method of B3LYP with the basis set of LanL2DZ
These basis set and pseudo potentials are chosen because some of the molecules are quite big with Al in it which is on the 3rd row of the periodic table.
Below are the results.
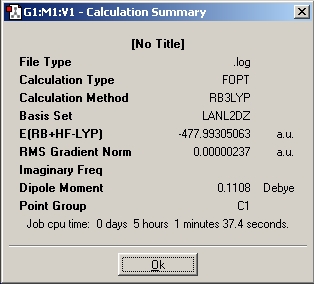
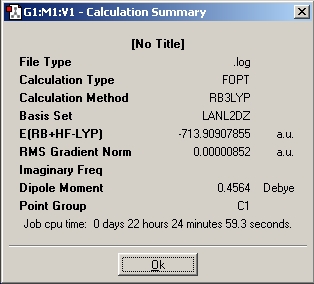
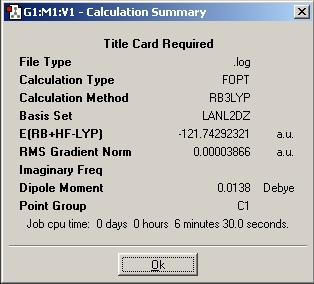
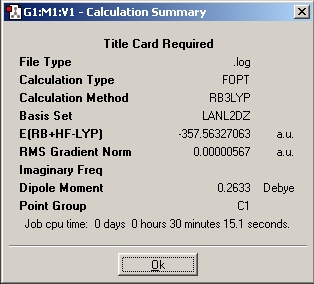
Summary for Al2(R)6 where R=CH3
Summary for Al2(R)6 where R=C2H5
Summary for Al2(R)6 where R=C3H7
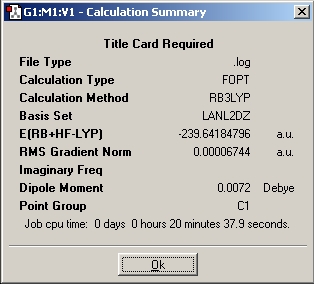
Summary for Al(R)3 where R=CH3
Summary for Al(R)3 where R=C2H5
Summary for Al(R)3 where R=C3H7
Geometry and Energies
| Al2(R)6 | Lit Value | AlR3 | Lit Value | |
|---|---|---|---|---|
| Optimised structure |
|
|
||
| Al-R distance (A) | 2.74576( to bridging) 1.98520 (to terminal) | 2.12 ( to bridging) 1.95 (to terminal) | 1.98559 | / |
| Al-R-Al angle (°) | 114.748 | 75 | / | / |
| Energy (a.u.) | -242.26852619 | / | -121.74292321 | / |
The resutls shown that for the Al2(R)6 the optimisation is not very sucessful as the bond angle is very different from the lit. value.
| Al2(R)6 | Lit Value | AlR3 | Lit Value | |
|---|---|---|---|---|
| Optimised structure |
|
|
||
| Al-R distance (A) | 2.01358( to bridging) 2.01626 (to terminal) | 2.12 ( to bridging) 1.95 (to terminal) | 1.99575 | / |
| Al-R-Al angle (°) | 80.546 | 75 | / | / |
| Energy (a.u.) | -477.99305063 | / | -239.64184796 | / |
This time the optimsation is more sucessful as it is much closer to the lit value
| Al2(R)6 | Lit Value | AlR3 | Lit Value | |
|---|---|---|---|---|
| Optimised structure |
|
|
||
| Al-R distance (A) | 2.00060( to bridging) 1.99828 (to terminal) | 2.12 ( to bridging) 1.95 (to terminal) | 1.99709 | / |
| Al-R-Al angle (°) | 137.359 | 75 | / | / |
| Energy (a.u.) | -713.90907855 | / | -351.56327063 | / |
IR
Al2(R)6 where R=CH3
Al2(R)6 where R=C2H5
Al2(R)6 where R=C3H7
Al(R)3 where R=CH3
Al(R)3 where R=C2H5
Al(R)3 where R=C3H7
When R is a Halogen
When the bridging atomes are halides the Al-X-Al angle will be close to 90 degree, because the halogen atom has more orbitals and electron available to form a bridge utilizing the 2 2c2e bonds
Here I have chosen to replace the R group with a chloride.
summary
The Al2Cl6 and AlCl3 molecules are optimised using the same method as before and here are the results.
| Al2(R)6 | Lit Value | AlR3 | Lit Value | |
|---|---|---|---|---|
| Optimised structure |
|
|
||
| Al-R distance (A) | 2.41510( to bridging) 2.17493(to terminal | 2.3 ( to bridging) | 1.98559 | / |
| Al-R-Al angle (°) | 94.444 | 91 | / | / |
| Energy (a.u.) | -94.04565810 | / | -47.00507023 | / |
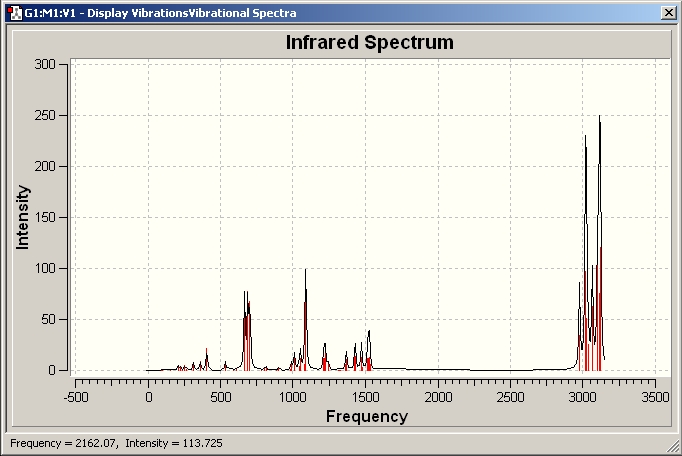
This time the calcuated values are very closed to the lit value. meaning the optimasation has been sucessful
IR
Al2Cl6
AlCl3
Reference
- D.F. Shriver and P.W. Atkins, "Inorganic Chemistry", 1999, 3rd Edition., p.518