Jump to content

Rep:Mod:fb618

From ChemWiki

NH3

NH3 Summary Information

Molecule name NH3
Calculation method RB3LYP
Basis Set 6-31G(d,p)
Final Energy E(RB3LYP) in au -56.55776873
RMS gradient in au 0.00000485
Point group of the molecule C3v

NH3 Item section

 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES


NH3 Jmol file

NH3 Optimised File

The optimisation file can be viewed here

NH3 Key structural information

Optimised N-H bond distance: 1.02 Å

Optimised H-N-H bond angle: 106°


NH3 Display Vibrations

The calculation was successful as there are no negative vibrational frequencies shown in the table.

NH3 Vibrations and Frequencies

NH3 vibrational modes
Wavenumber in cm-1 1090 1694 1694 3461 3590 3590
Symmetry label A1 E E A1 E E
IR Intensity in arbitrary units 145 14 14 1 ~ 0 ~ 0
Image

Number of expected modes from 3N-6 rule = 3*4-6 = 6

Degeneracy

Modes with energy 1694 cm-1 and symmetry label E are degenerate. The modes with energy 3590 cm-1 and symmetry label E are also degenerate.

Bending Vibrations

The wagging mode at 1090 cm-1 is a bending vibration. It is Raman active since the polizability of the molecule changes. It is also the most IR active mode of NH3 which is reflected in the high IR intensity of 145. The mode can be IR and Raman active because NH3 does not have a centre of inversion.

The two degenerate scissoring modes at 1694 cm-1 are also bending vibrations. The modes are IR active as there is a change in dipole moment. The IR activity is reflected in the calculated IR intensity of 14. The modes are also raman active.

Bond stretches

The symmetric stretch at 3461 cm-1 is a stretching mode. It is Raman active as expected since the size of the molecule changes by a large amount, which changes the polarizablilty of the molecule. Since the stretch is symmetric though there is not change in dipole moment. Therefore the stretch is not IR active, shown by the very low IR Intensity of 1.

The two degenerate asymmetric stretches at 3590 cm-1 are also Raman active. They are not IR active because the changes in dipole moment due to the stretch cancel each other out so that the overall change in dipole moment is almost 0 as shown by the data.

Special vibrational modes

The symmetric stretch at 3461 cm-1 is also called the highly symmetric mode. It has the symmetry label A1.

Another special vibrational mode is the umbrella mode at 1090 cm-1.

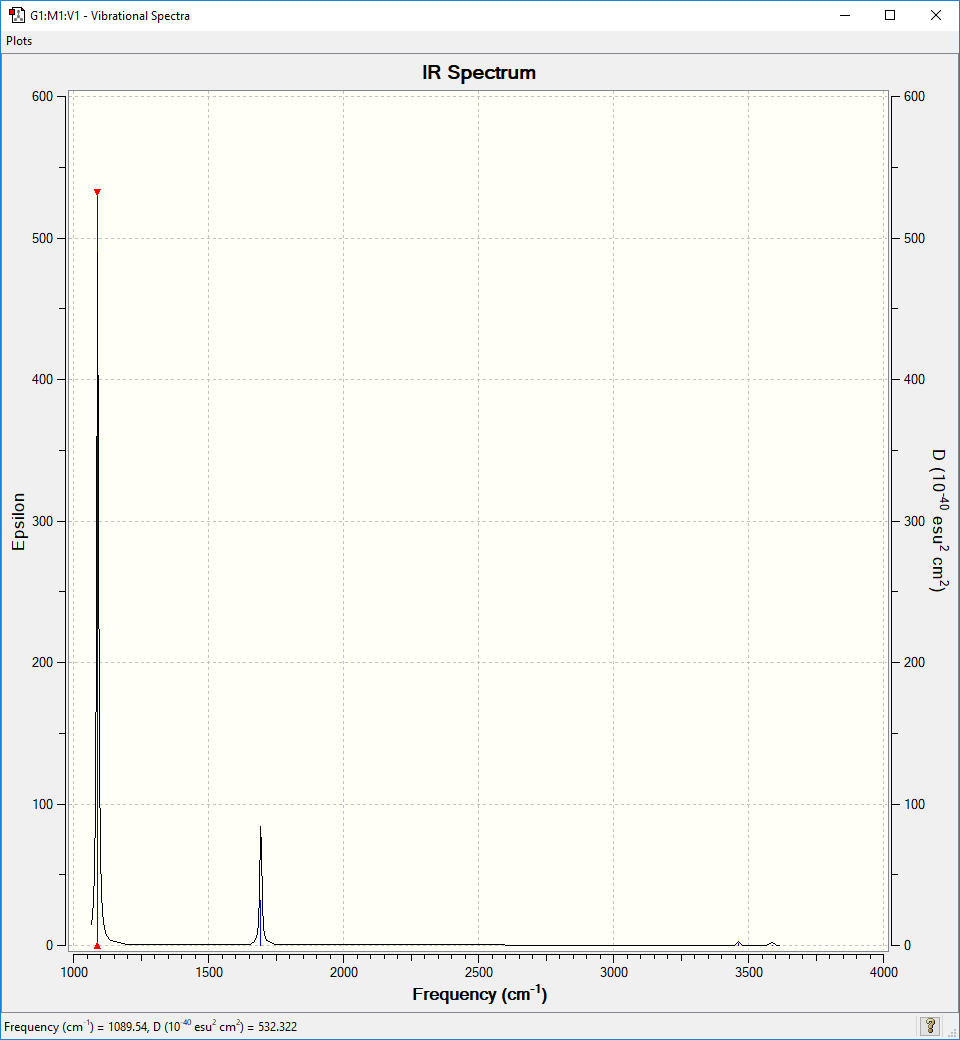
IR spectrum

2 distinct peaks are expected in the IR spectrum since there are only 2 non degenerate IR active vibrational modes with an IR intensity high enough to be observed. The peaks are expected at 1090 cm-1 and 1694 cm-1. The spectrum clearly shows these peaks.

NH3 NBO Charge Analysis

The nitrogen atom is expected to have a negative charge since it has a higher electronegativity than the hydrogen atoms.

Charge on the nitrogen atom: -1.124

Charge on the hydrogen atoms: +0.375



H2

H2 Summary Information

Molecule name H2
Calculation method RB3LYP
Basis Set 6-31G(d,p)
Final Energy E(RB3LYP) in atomic units -1.17853936
RMS gradient in atomic units 0.00000017
Point group of the molecule D∞h


H2 Item section

 
Item          Value     Threshold        Converged?
Maximum Force            0.000000     0.000450     YES
RMS     Force            0.000000     0.000300     YES
Maximum Displacement     0.000000     0.001800     YES
RMS     Displacement     0.000001     0.001200     YES


H2 Jmol file

H2 Optimised File

The optimisation file can be viewed here

H2 Key structural information

Optimised H-H bond distance: 0.74Å

H2 Display Vibrations

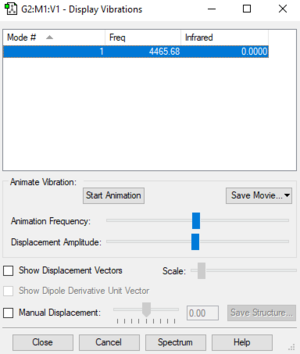
The calculation was successful as there are no negative vibrational frequencies shown in the table.


H2 Vibrations and Frequencies

H2 vibrational modes
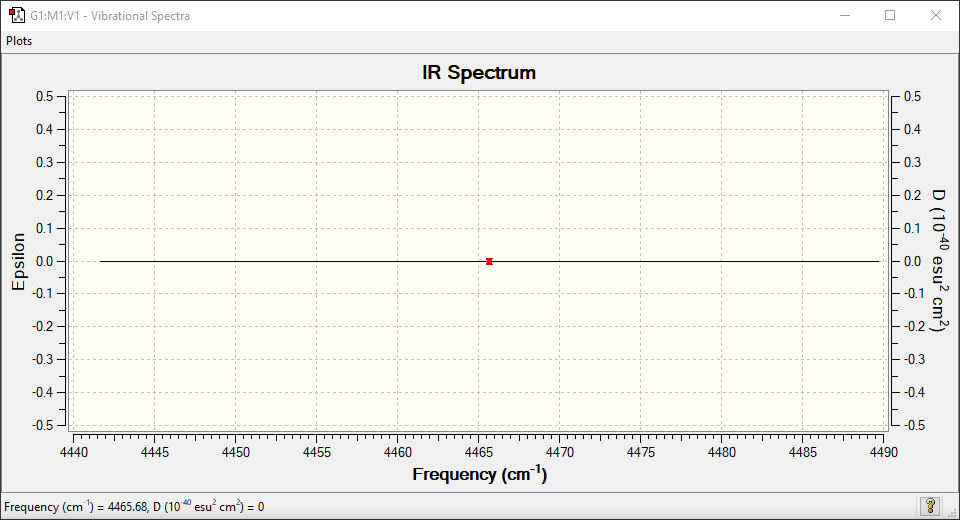
Wavenumber in cm-1 4466
Symmetry SGG
IR Intensity in arbitrary units 0
Image

Number of expected modes from 3N-5 rule = 3*2-5 = 1

0 bands are expected in the IR spectrum since there are no IR active vibrational modes. The spectrum clearly shows a perfect flat line since there is absolutely no change in dipole moment.

H2 NBO Charge Analysis

Both hydrogen atoms are expected to have a charge of 0 because there is no electronegativity difference.

Charge on each hydrogen atom: 0



N2

N2 Summary Information

Molecule name N2
Calculation method RB3LYP
Basis Set 6-31G(d,p)
Final Energy E(RB3LYP) in atomic units -109.52412868
RMS gradient in atomic units 0.00000217
Point group of the molecule D∞h

N2 Item section

 
        Item                Value    Threshold  Converged?
Maximum Force            0.000004     0.000450     YES
RMS     Force            0.000004     0.000300     YES
Maximum Displacement     0.000001     0.001800     YES
RMS     Displacement     0.000002     0.001200     YES

N2 Jmol file

N2 Optimised File

The optimisation file can be viewed here

N2 Key structural information

Optimised N-N bond distance: 1.11 Å

N2 Display Vibrations

The calculation was successful as there are no negative vibrational frequencies shown in the table.


N2 Vibrations and Frequencies

N2 vibrational modes
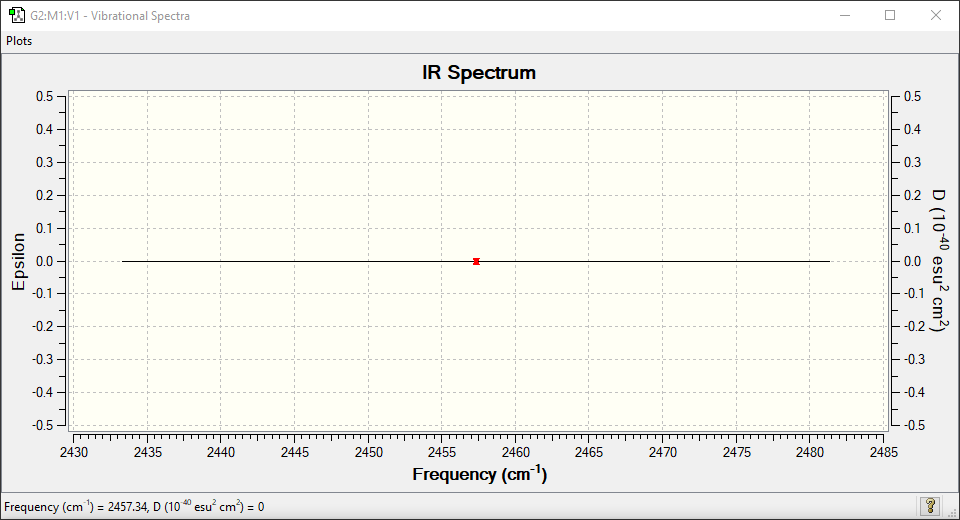
Wavenumber in cm-1 2457
Symmetry SGG
IR Intensity in arbitrary units 0
Image

Number of expected modes from 3N-5 rule = 3*2-5 = 1

There are no peaks expected in the IR spectrum since there are no IR active vibrational modes. The spectrum below clearly shows a perfect flat line.

N2 NBO Charge Analysis

Both nitrogen atoms are expected to have a charge of 0 because there is no electronegativity difference.

Charge on each nitrogen atom: 0

N2 HOMO/LUMO

Orbital Image Energy in au
HOMO 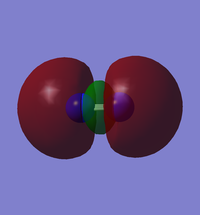-0.42688
LUMO -0.02412

N2 as ligands

CCDC identifier of Complex with N2 ligand DEKFUX
N2 bond length in complex 1.086(6) Å
N2 bond length obtained 1.11 Å
Link to sample structure [[1]]

The bond length found in the complex is shorter than the bond length obtained from the calculation. This result would mean that electron density is donated from the complex towards the ligand. This is called backdonation. However, since Ruthenium complexes are not usually known to undergo this, a computational error is more likely. Further error could be introduced through the experimental determination of the bond length.

Energies in the Haber Process

E(NH3) in atomic units to 7 d.p. -56.5577687
2*E(NH3) in atomic units to 7 d.p. -113.1155375
E(N2) in atomic units to 7 d.p. -109.5241287
E(H2) in atomic units to 7 d.p. -1.1785394
3*E(H2) in atomic units to 7 d.p. -3.5356181
ΔE in atomic units to 7 d.p. -0.0557907
ΔE in kJmol-1 to 1 d.p. -146.5

Ammonia gas is more stable than hydrogen gas and nitrogen gas because the overall enthalpy ΔE change is -146.5 kJmol-1 is negative.

SiH4

SiH4 Summary Information

Molecule name SiH4
Calculation method RB3LYP
Basis Set 6-31G(d,p)
Final Energy E(RB3LYP) in atomic units -291.88802760
RMS gradient in atomic units 0.00000002
Point group of the molecule Td

SiH4 Item section

 
         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES


SiH4 Jmol file

SiH4 Optimised File

The optimisation file can be viewed here

SiH4 Key structural information

Optimised Si-H bond distance: 1.48 Å

Optimised H-Si-H bond angle: 109.47°

SiH4 Display Vibrations

The calculation was successful as there are no negative vibrational frequencies shown in the table.

SiH4 Vibrations and Frequencies

SiH4 vibrational modes
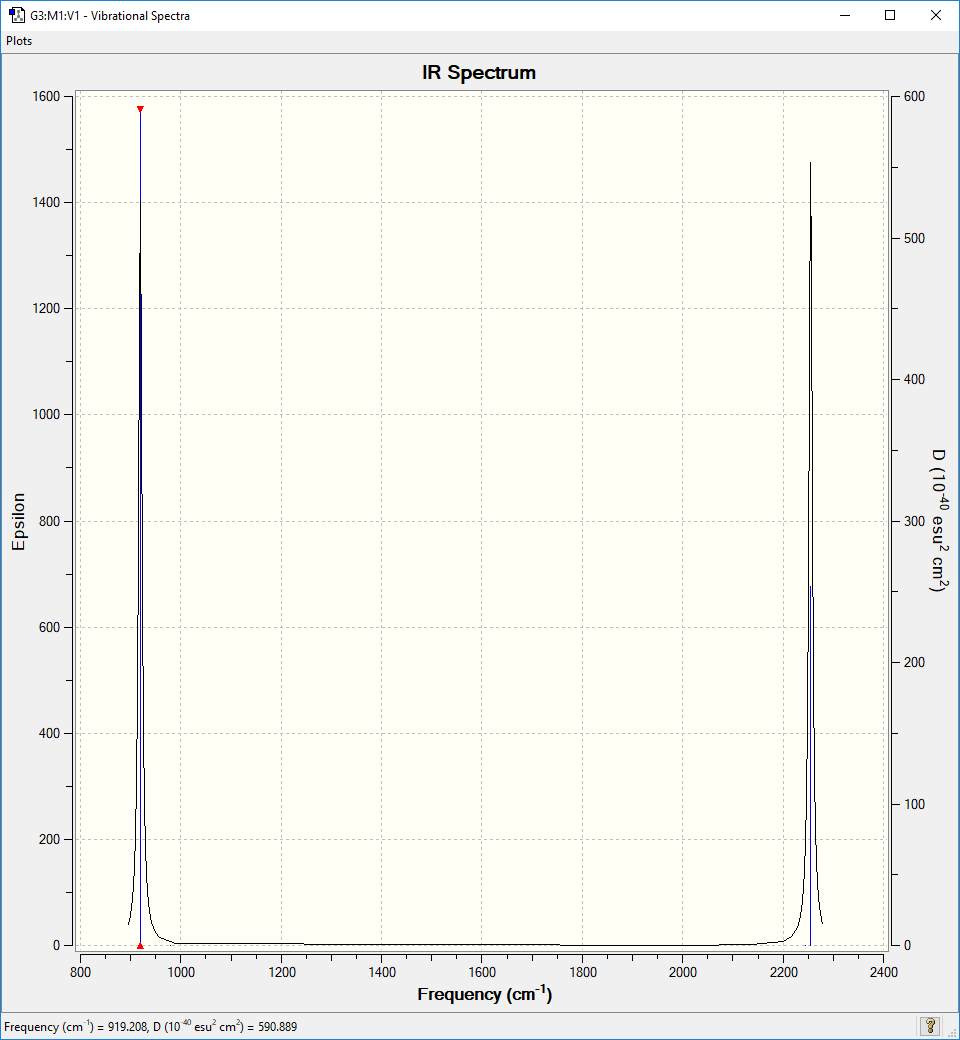
Wavenumber in cm-1 919 919 919 979 979 2244 2255 2255 2255
Symmetry T2 T2 T2 E E A1 T2 T2 T2
IR Intensity in arbitrary units 136 136 136 0 0 0 143 143 143
Image

Number of expected modes from 3N-6 rule = 3*5-6 = 9

Degeneracy

The 3 modes at 919 cm-1 and symmetry label T2 are degenerate as well as the 2 modes at 979 cm-1 and symmetry label E. The 3 modes at 2255 cm-1 and symmetry label T2 are also degenerate.

Bending Vibrations

The three degenerate wagging modes with symmetry label T2 at 919 cm-1 are bending vibrations. They are IR active as there is a change in dipole moment. They are also Raman active. The modes can be Raman active and IR active since SiH4 doesn't have a centre of inversion. The IR activity is reflected in the high IR intensity value of 136 obtained through the calculation.

The two degenerate scissoring modes with symmetry label E at 979 cm-1 are also bending vibrations. They are not IR active since there is no change in dipole moment. They are Raman active.

Bond stretches

The symmetric stretch with symmetry label A1 at 2244 cm-1 is a stretching mode. It is not IR active since all changes in Dipole moment resulting from changes in individual Si-H bond lengths cancel each other out. The mode is Raman active.

The 3 degenerate asymmetric stretches with symmetry label T2 at 2255 cm-1 are also stretching vibrations. They are the most IR active modes in the molecule since they have an IR intensity value of 143, the highest of all stretches in the molecule. The 3 modes are also Raman active.

IR spectrum

There are 2 peaks expected in the IR spectrum since there are only 2 non degenerate IR active vibrational modes. The peaks are expected at 919 cm-1 and 2255 cm-1. The spectrum clearly shows these peaks.

SiH4 NBO Charge Analysis

The silicon atom is expected to have a positive charge since it has a lower electronegativity than the hydrogen atoms.

Charge on the silicon atom: +0.629

Charge on the hydrogen atoms: -0.157

SiH4 MO analysis

Silicon electron configuration: 1s22s22p63s23p2

Hydrogen electron configuration: 1s1

SiH4 Orbitals
MO number 1 2 3 6 7 10 13
Energy in au -66.12596 -5.28056 -3.63858 -0.54726 -0.35184 +0.05053 +0.12286
Occupancy 2 3 2 2 2 0 0
Type non bonding non bonding non bonding A1 bonding T2 bonding, HOMO T2 antibonding, LUMO A1 antibonding
AO contributions Si 1s Si 2s Si 2p Si 3s and 4*H 2s and 4*H 1s Si 3p and 4p and 4*H 2s Si 3p and 4p and 4*H 2s Si 3s and 4*H 2s
Degeneracy 1 1 3 1 3 3 1
Image 
 
                           1         2         3         4         5
                        (A1)--O   (A1)--O   (T2)--O   (T2)--O   (T2)--O
     Eigenvalues --   -66.12596  -5.28056  -3.63858  -3.63858  -3.63858
   1 1   Si 1S          0.99660  -0.26806   0.00000   0.00000   0.00000
   2        2S          0.01292   1.02338   0.00000   0.00000   0.00000
   3        2PX         0.00000   0.00000   0.00000   0.00000   0.99148
   4        2PY         0.00000   0.00000   0.99148   0.00000   0.00000
   5        2PZ         0.00000   0.00000   0.00000   0.99148   0.00000
   6        3S         -0.02764   0.07827   0.00000   0.00000   0.00000
   7        3PX         0.00000   0.00000   0.00000   0.00000   0.03151
   8        3PY         0.00000   0.00000   0.03151   0.00000   0.00000
   9        3PZ         0.00000   0.00000   0.00000   0.03151   0.00000
  10        4S          0.00432  -0.01660   0.00000   0.00000   0.00000
  11        4PX         0.00000   0.00000   0.00000   0.00000  -0.00789
  12        4PY         0.00000   0.00000  -0.00789   0.00000   0.00000
  13        4PZ         0.00000   0.00000   0.00000  -0.00789   0.00000
  14        5XX         0.00972  -0.01932   0.00000   0.00000   0.00000
  15        5YY         0.00972  -0.01932   0.00000   0.00000   0.00000
  16        5ZZ         0.00972  -0.01932   0.00000   0.00000   0.00000
  17        5XY         0.00000   0.00000   0.00000   0.00095   0.00000
  18        5XZ         0.00000   0.00000   0.00095   0.00000   0.00000
  19        5YZ         0.00000   0.00000   0.00000   0.00000   0.00095
  20 2   H  1S          0.00016  -0.00068  -0.00042  -0.00042  -0.00042
  21        2S          0.00002   0.00028  -0.00047  -0.00047  -0.00047
  22        3PX         0.00009  -0.00022  -0.00007  -0.00007  -0.00043
  23        3PY         0.00009  -0.00022  -0.00043  -0.00007  -0.00007
  24        3PZ         0.00009  -0.00022  -0.00007  -0.00043  -0.00007
  25 3   H  1S          0.00016  -0.00068   0.00042  -0.00042   0.00042
  26        2S          0.00002   0.00028   0.00047  -0.00047   0.00047
  27        3PX        -0.00009   0.00022  -0.00007   0.00007  -0.00043
  28        3PY        -0.00009   0.00022  -0.00043   0.00007  -0.00007
  29        3PZ         0.00009  -0.00022   0.00007  -0.00043   0.00007
  30 4   H  1S          0.00016  -0.00068  -0.00042   0.00042   0.00042
  31        2S          0.00002   0.00028  -0.00047   0.00047   0.00047
  32        3PX        -0.00009   0.00022   0.00007  -0.00007  -0.00043
  33        3PY         0.00009  -0.00022  -0.00043   0.00007   0.00007
  34        3PZ        -0.00009   0.00022   0.00007  -0.00043  -0.00007
  35 5   H  1S          0.00016  -0.00068   0.00042   0.00042  -0.00042
  36        2S          0.00002   0.00028   0.00047   0.00047  -0.00047
  37        3PX         0.00009  -0.00022   0.00007   0.00007  -0.00043
  38        3PY        -0.00009   0.00022  -0.00043  -0.00007   0.00007
  39        3PZ        -0.00009   0.00022  -0.00007  -0.00043   0.00007
                           6         7         8         9        10
                        (A1)--O   (T2)--O   (T2)--O   (T2)--O   (T2)--V
     Eigenvalues --    -0.54726  -0.35184  -0.35184  -0.35184   0.05053
   1 1   Si 1S          0.05925   0.00000   0.00000   0.00000   0.00000
   2        2S         -0.27507   0.00000   0.00000   0.00000   0.00000
   3        2PX         0.00000  -0.16968   0.00000   0.00000   0.00000
   4        2PY         0.00000   0.00000   0.00000  -0.16968  -0.09878
   5        2PZ         0.00000   0.00000  -0.16968   0.00000   0.00000
   6        3S          0.58223   0.00000   0.00000   0.00000   0.00000
   7        3PX         0.00000   0.40049   0.00000   0.00000   0.00000
   8        3PY         0.00000   0.00000   0.00000   0.40049   0.30912
   9        3PZ         0.00000   0.00000   0.40049   0.00000   0.00000
  10        4S          0.13912   0.00000   0.00000   0.00000   0.00000
  11        4PX         0.00000   0.09051   0.00000   0.00000   0.00000
  12        4PY         0.00000   0.00000   0.00000   0.09051   1.32295
  13        4PZ         0.00000   0.00000   0.09051   0.00000   0.00000
  14        5XX        -0.01270   0.00000   0.00000   0.00000   0.00000
  15        5YY        -0.01270   0.00000   0.00000   0.00000   0.00000
  16        5ZZ        -0.01270   0.00000   0.00000   0.00000   0.00000
  17        5XY         0.00000   0.00000   0.07455   0.00000   0.00000
  18        5XZ         0.00000   0.00000   0.00000   0.07455  -0.14210
  19        5YZ         0.00000   0.07455   0.00000   0.00000   0.00000
  20 2   H  1S          0.12832   0.17278   0.17278   0.17278  -0.08967
  21        2S          0.08859   0.19100   0.19100   0.19100  -0.65470
  22        3PX        -0.00647  -0.00112  -0.00463  -0.00463  -0.00561
  23        3PY        -0.00647  -0.00463  -0.00463  -0.00112   0.01247
  24        3PZ        -0.00647  -0.00463  -0.00112  -0.00463  -0.00561
  25 3   H  1S          0.12832  -0.17278   0.17278  -0.17278   0.08967
  26        2S          0.08859  -0.19100   0.19100  -0.19100   0.65470
  27        3PX         0.00647  -0.00112   0.00463  -0.00463  -0.00561
  28        3PY         0.00647  -0.00463   0.00463  -0.00112   0.01247
  29        3PZ        -0.00647   0.00463  -0.00112   0.00463   0.00561
  30 4   H  1S          0.12832  -0.17278  -0.17278   0.17278  -0.08967
  31        2S          0.08859  -0.19100  -0.19100   0.19100  -0.65470
  32        3PX         0.00647  -0.00112  -0.00463   0.00463   0.00561
  33        3PY        -0.00647   0.00463   0.00463  -0.00112   0.01247
  34        3PZ         0.00647  -0.00463  -0.00112   0.00463   0.00561
  35 5   H  1S          0.12832   0.17278  -0.17278  -0.17278   0.08967
  36        2S          0.08859   0.19100  -0.19100  -0.19100   0.65470
  37        3PX        -0.00647  -0.00112   0.00463   0.00463   0.00561
  38        3PY         0.00647   0.00463  -0.00463  -0.00112   0.01247
  39        3PZ         0.00647   0.00463  -0.00112  -0.00463  -0.00561
                          11        12        13        14        15
                        (T2)--V   (T2)--V   (A1)--V   (A1)--V   (T2)--V
     Eigenvalues --     0.05053   0.05053   0.12286   0.22050   0.23395
   1 1   Si 1S          0.00000   0.00000   0.07481  -0.01739   0.00000
   2        2S          0.00000   0.00000  -0.18524  -0.12336   0.00000
   3        2PX         0.00000  -0.09878   0.00000   0.00000  -0.28916
   4        2PY         0.00000   0.00000   0.00000   0.00000   0.00000
   5        2PZ        -0.09878   0.00000   0.00000   0.00000   0.00000
   6        3S          0.00000   0.00000   1.59937  -1.06382   0.00000
   7        3PX         0.00000   0.30912   0.00000   0.00000   1.29279
   8        3PY         0.00000   0.00000   0.00000   0.00000   0.00000
   9        3PZ         0.30912   0.00000   0.00000   0.00000   0.00000
  10        4S          0.00000   0.00000  -0.09324   3.88850   0.00000
  11        4PX         0.00000   1.32295   0.00000   0.00000  -0.98187
  12        4PY         0.00000   0.00000   0.00000   0.00000   0.00000
  13        4PZ         1.32295   0.00000   0.00000   0.00000   0.00000
  14        5XX         0.00000   0.00000  -0.03699   0.05295   0.00000
  15        5YY         0.00000   0.00000  -0.03699   0.05295   0.00000
  16        5ZZ         0.00000   0.00000  -0.03699   0.05295   0.00000
  17        5XY        -0.14210   0.00000   0.00000   0.00000   0.00000
  18        5XZ         0.00000   0.00000   0.00000   0.00000   0.00000
  19        5YZ         0.00000  -0.14210   0.00000   0.00000  -0.00915
  20 2   H  1S         -0.08967  -0.08967  -0.08792  -0.14418   0.01627
  21        2S         -0.65470  -0.65470  -0.51186  -1.07842  -0.17337
  22        3PX        -0.00561   0.01247  -0.00878   0.00647  -0.00174
  23        3PY        -0.00561  -0.00561  -0.00878   0.00647  -0.01177
  24        3PZ         0.01247  -0.00561  -0.00878   0.00647  -0.01177
  25 3   H  1S         -0.08967   0.08967  -0.08792  -0.14418  -0.01627
  26        2S         -0.65470   0.65470  -0.51186  -1.07842   0.17337
  27        3PX         0.00561   0.01247   0.00878  -0.00647  -0.00174
  28        3PY         0.00561  -0.00561   0.00878  -0.00647  -0.01177
  29        3PZ         0.01247   0.00561  -0.00878   0.00647   0.01177
  30 4   H  1S          0.08967   0.08967  -0.08792  -0.14418  -0.01627
  31        2S          0.65470   0.65470  -0.51186  -1.07842   0.17337
  32        3PX        -0.00561   0.01247   0.00878  -0.00647  -0.00174
  33        3PY         0.00561   0.00561  -0.00878   0.00647   0.01177
  34        3PZ         0.01247  -0.00561   0.00878  -0.00647  -0.01177
  35 5   H  1S          0.08967  -0.08967  -0.08792  -0.14418   0.01627
  36        2S          0.65470  -0.65470  -0.51186  -1.07842  -0.17337
  37        3PX         0.00561   0.01247  -0.00878   0.00647  -0.00174
  38        3PY        -0.00561   0.00561   0.00878  -0.00647   0.01177
  39        3PZ         0.01247   0.00561   0.00878  -0.00647   0.01177

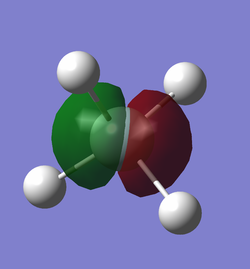
As we can see in the data table of the LOG file, for the first MO the contribution of the silicon 1s orbital is 0.99660. The contribution of the silicon 2s orbital is 0.01292. There is also some negative contribution from the silicon 3s orbital. Each hydrogen 1s orbital has a positive contribution of only 0.00016. That means it is almost a complete non bonding orbital. We can see in the diagram how small it is around the silicon atom.

The 2nd MO has a contribution of 1.02338 from the 2s orbital. There is some negative contribution from the 1s orbital and only 0.00028 positive contribution from each hydrogen 2s orbital. Therefore this orbital is also an almost complete non bonding orbital. The diagram shows that the MO is closely centred around the silicon nucleus.

The 3rd, 4th and 5th MO are degenerate and have a major contribution of 0.99148 from the silicon 2py, 2pz and 2px respectively. They also have small contributions of 0.03151 from the 3py, 3pz and 3px respectively. Each of the MOs has a slight contribution of 0.00042 from 2 of the hydrogen 1s AOs and a slight contribution of 0.00047 from 2 of the hydrogen 2s AOs. Each MO also has the corresponding negative contribution from the other 2 hydrogens. Considering the very low contributions from the hydrogen AOs, these MOs are still non bonding MOs.

The 6th lowest energy MO has a contribution of 0.58223 from the silicon 3s orbital and a contribution of 0.13912 from the 4s orbital. It also has some further very small positive and negative contributions from other silicon AOs. However it has a significant contribution of 0.12832 from each of the 4 hydrogen 1s AOs. It also has a contribution of 0.08859 from each of the hydrogen 2s AOs. This MO has significant bonding character which is represented in the diagram by the shared electron density between the hydrogen and silicon nuclei. This MO is often represented as the overlap between the in-phase hydrogen LGO with the 3s of the silicon in the same phase.

The 7th, 8th and 9th lowest energy MO are degenerate and have a contribution of 0.40049 from the silicon 3px AO, 3pz AO and 3py AO respectively. They also have a low contribution of 0.09051 from the corresponding 4p silicon AO. All three MOs have a positive contribution of 0.17278 from each hydrogen 1s AO and a contribution of 0.19100 from each hydrogen 2s AO. Each MO also has a positive contribution of 0.00463 from 4 of the 12 hydrogen 3p AOs and small negative contributions from the other hydrogen 3p AOs. These degenerate MOs are often modelled as the bonding overlap between the out-of-phase hydrogen LGOs and the silicon 3p AOs. We can see this overlap in the diagram as the 2 lobes of shared electron distribution between the silicon and 2 hydrogen atoms each. These MOs are also the highest occupied molecular orbitals, so they play essential part in the reactivity of the molecule.

Marking

Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.

Wiki structure and presentation 1/1

Is your wiki page clear and easy to follow, with consistent formatting?

YES - good overall, well done.

Do you effectively use tables, figures and subheadings to communicate your work?

YES - although you could have reduced the sizes of some figures.

NH3 1/1

Have you completed the calculation and given a link to the file?

YES

Have you included summary and item tables in your wiki?

YES

Have you included a 3d jmol file or an image of the finished structure?

YES

Have you included the bond lengths and angles asked for?

YES

Have you included the “display vibrations” table?

YES

Have you added a table to your wiki listing the wavenumber and intensity of each vibration?

YES

Did you do the optional extra of adding images of the vibrations?

YES

Have you included answers to the questions about vibrations and charges in the lab script?

YES - excellent detailed explanations.

N2 and H2 0.5/0.5

Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)

YES

Crystal structure comparison 0.5/0.5

Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?

YES

Have you compared your optimised bond distance to the crystal structure bond distance?

YES - good consideration of possible factors.

Haber-Bosch reaction energy calculation 1/1

Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]

YES

Have you reported your answers to the correct number of decimal places?

YES

Do your energies have the correct +/- sign?

YES

Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?

YES

Your choice of small molecule 4/5

Have you completed the calculation and included all relevant information?

YES

Have you added information about MOs and charges on atoms?

YES, overall a good explanation of the contributions from the AOs to the MOs. However please note that the contributions of the basis functions (as tabulated in the log file) do not necessarily correlations exactly with the AO contributions. Basis functions are not exact replicas of atomic AOs, and further differences will occur when molecules are modelled. I would have liked you to note that MOs 3, 4 and 5 are the bonding, in-phase MOs between Si 3p and H LGOs, and MOs 7, 8 and 9 are the corresponding antibonding MOs. In general you haven't discussed the antibonding/bonding nature of the MOs and their contributions to the bonding in the molecule. Please see the included diagram for more info.

SiH4 MOs

Independence 0/1

If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or Do some deeper analysis on your results so far

Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:fb618&oldid=819224"