Rep:Mod:farie-att
Vibrational and MO analysis of BH3
BH3 molecule
The BH3 molecule was drawn in Gaussview and the geometry was optimised using Gaussian. The DFT B3LYP method was used and the basis set was set to 3-21G. The frequency was calculated using the same method and basis set. The molecule has 6 vibrational modes but less than six peaks show up in the spectrum. This is because some of the vibrations have the same frequency, therefore their peaks overlap. IR spectroscopy measures change in dipole moment of the molecule as it vibrates. Vibration number 4 is totally symmetric and has a dipole moment of zero and so it does not appear on the spectrum as its intensity is zero. The following table shows the vibrational modes of BH3.
BH3 vibrational analysis
| No | Form of the vibration | Frequency cm-1 | Intensity | Symmetry D3H point group |
|---|---|---|---|---|
| 1 |  |
1144.15 | 92.87 | A"2 Totally symmetric in plane perpendicular to principle axis. |
| 2 |  |
1203.64 | 12.31 | E' Antisymmetric in plane perpindicular to principle axis, similar to P(y) orbital. |
| 3 |  |
1203.64 | 12.31 | E' Antisymmetric In plane perpindicular to principle axis, similar to P(x) orbital. |
| 4 |  |
2598.42 | 0.0 | A'1 Totally symmetric |
| 5 |  |
2737.44 | 103.74 | E' Antisymmetric in plane perpindicular to principle axis, similar to P(y) orbital. |
| 6 |  |
2737.44 | 103.73 | E' Antisymmetric in plane perpindicular to principle axis, similar to P(x) orbital. |
The molecular orbitals of BH3 were generated by setting the job type to “energy” and using the same method and basis set (3-21G) used for the optimisation. The additional words “pop=full” were added to the input file and the NBO was set to full. The real molecular orbitals are very similar to the ones predicted using the LCAO. The only difference is the way in which the orbitals are drawn, in LCAO the molecular orbitals are drawn as discrete atomic orbitals, the real MOs are mixed. The molecular orbitals agree with those obtained using LCAO up to the LUMO level only, the computed unoccupied MOs appear to be more diffuse and have unusual shapes compared to those predicted by LCAO.This shows that the MO theory is useful and quite accurate in predicting the shape of the real MOs.
The NBO analysis showed the boron to be highly positive an the hydrogens to be negative. The empty 2pz orbital on the boron was found to have a negative energy. This is unusual because unoccupied orbital usually have positive energies. This shows the Lewis acid nature of the molecuela as it is able to accept electron into a low lying empty orbital.
BH3 otpimisation file
https://www.ch.ic.ac.uk/wiki/index.php/Image:FARIE_BH3_OPT.LOG
BH3 frequency file https://www.ch.ic.ac.uk/wiki/index.php/Image:FARIE_BH3_FREQ.LOG
BH3 population file https://www.ch.ic.ac.uk/wiki/index.php/Image:FARIE_BH3_POP.LOG
Structural Analysis of BCl3
BCl3 molecule
The BCl3 structure was drawn using Gaussview, the geometry was then optimised using Gaussian. The method employed was the DFT (density functional theory) B3LYP method. The LanL2MB basis set was used; this is a medium level basis set, which is used when a molecule contains heavy atoms, chlorine in this case. The symmetry of the BCl3 was restricted by setting the point group to D3h. The same method and basis set were used for the frequency and optimisation calculations. A fully optimised structure for the LanL2MB basis set was used for the frequency calculation. Using a different method and basis sets means the electron density calculations will be different. Using a higher level basis set to calculate the frequency on a structure optimised using a lower level basis will give an excited electron density frequency. The optimization calculation took 8 seconds and the frequency calculation took 20 seconds.
The optimisation of a molecular structure, is done to find the stable point (ideally where the gradient is zero and is a minimum) on the potential energy surface. Optimising a structure does not however tell us whether the structure obtained is the minimum energy conformation; it only allows us to improve the structure of the molecule to find the structure that gives the minimum energy. On a graph of the potential energy vs the reaction coordinate, the gradient tell us where there is a point of inflexion (gradient=0), but it does not tell us whether it is a maximum (transition state) or a minimum (ground state). The second derivative tells whether the point of inflexion is a minimum (+ve value) or maximum (-ve value). The frequency analysis can be thought of as the second derivative of the potential energy surface. If all frequencies are positive, then it is a minimum, if one is negative then it is a transition state and if there are more negative frequencies, then it means the optimisation is incomplete or has failed. The frequency also provides the IR and Raman modes to compare with experimental values.
The B-Cl bond length of 1.866 Å, the literature value is 1.750Å The Cl-B-Cl bond anlges are all 120⁰, the literature value is 120⁰ DOI:10.1021/ic990713
In some structures Guassview does not draw in bonds where they would be expected, this does not mean there is no bond. Gaussview has a list of bond distances, which are set mainly for organic compounds. If the bond lengths are longer than the listed ones, Gaussview does not draw them in, bond lengths are usually longer in inorganic complexes than in organic compounds.
Two atoms can interact to form a molecule. A bond is an attractive interaction between two atoms which then form a molecule. If formation of the bond is favourable, then the atoms will have a lower energy (more stabilised) as a molecule, compared to when they are separate. An ionic bond is an interaction between two oppositely charged species (atoms). A bond involves a distribution of electron density between two atoms either equally or unequally. In a bond electron density can lie more on one atom than the other or be found distributed equally between the two atoms.
BCl3 is expected to have a D3h symmetry point group. When calculating the optimization, the symmetry of BCl3 was set to D3h. A calculation does not change the symmetry of the molecule; it only computes the lowest energy for that particular symmetry. Gaussview is not good at imposing symmetry therefore it uses the C1 symmetry. To do a high symmetry calculation, the coordinates and symmetry of the molecule have to be imposed manually. Imposing symmetry forces the program to set certain values through symmetry relationships rather than computing them, this can make calculations faster for highly symmetric molecules.
BCl3 optimization file https://www.ch.ic.ac.uk/wiki/index.php/Image:FARIE_BCL3_OPT.LOG
BCl3 frequency file https://www.ch.ic.ac.uk/wiki/index.php/Image:FARIE_BCL3_FREQ.LOG
Cis, trans Mo(CO)4(PCl3)2 isomers
cis Mo(CO)4(PCl3)2
trans Mo(CO)4(PCl3)2
The trans isomer is arranged in such a way that the chlorides on the phosphine ligands are eclipsed. The M-P bonds are longer in the cis isomer (2.512Å) compared to the trans isomer (2.445Å). The trans isomer has higher symmetry than the cis isomer.
In the cis isomer, the equatorial C=O bond lengths (1.176Å) are longer than the axial C=O bond lengths (1.173Å). This is due to increased pi back donation from the metal to the CO pi antibonding orbital, this weakens the C=O bond and is reflected by the lengthening of the bond. The C=O bond lengths in the trans isomer are similar ~ 1.173Å each.
Cis Mo(CO)4(PCl3)2 -623.58 Hartree DOI:10042/to-3762
Trans Mo(CO)4(PCl3)2 -623.58 Hartree DOI:10042/to-3763
From the optimisation calculations, the cis isomer is more stable than the trans isomer as it is slightly lower energy. However the energy difference between the two isomers is quite small. The CO ligands are better at backbonding compared to the PCl3. The CO ligands also have a stronger trans effect. Due to pi backbonding from the metal to the carbonyl, the Mo-C bond is shorter and stronger compared to the Mo-P bond. The cis isomer is more stabilised because the Mo-P bond is longer, thus reducing the steric interaction between the cis phosphines. In the cis isomer, the equatorial carbonyl ligands are trans to the phosphine ligands, these carbonyl groups have higher backbonding to the metal compared to the axial carbonyl, this can be seen in that the equatorial Mo-C bond is 2.012 Å and the axial Mo-C is 2.058Å. This is because the phosphines are poor at backbonding therefore in the equatorial plane electron density form the metal is used to backbond to the two carbonyls, forming stronger Mo-C bonds. In the trans isomer, the M-C bond lights are about 2.060Å, as the carbonyl are equatorial, they have longer bonds. In the cis isomer the P-Mo-P angle is 94.2°, the equatorial C-Mo-C angle is 87.1° and the angles between the axial and equatorial ligands is approximately 90°. The slightly larger angle (P-Mo-P) combined with the longer bond lengths (Mo-P) reduces steric clashes in the cis isomer and stabilises the isomer. The cis isomer also has a reduced number of CO trans ligands which stabilises it compared to the trans isomer. The trans isomer is expected to have been the more stable isomer as the bulky phosphine ligands are far apart from each other, this would mean steric interactions are at their minimum. The C-M-C and P-M-C bond angles are approximately 90°. The Mo-C bond length is 2.060Å and the Mo-P bond length is 2.445Å. The energy difference is 0.00104Hartree = 2.73 kj/mol. This is a small energy difference.
All the frequencies obtained for the isomers were poistive which means that the structures are at an energy minimum. cis DOI:10042/to-3782 trans DOI:10042/to-3783 Both isomers had vibrations of very low frequency, whcich are vibrations of the P-Cl bonds.
| no | Form of the vibration | Frequency cm-1 | Intensity | Vibration description |
|---|---|---|---|---|
| 1 |  |
10.74 | 0.0264 | The rocking/ bending of the chlorine atoms, the carbonyl groups are displaced in a rocking motion only slightly. |
| 2 | .jpg) |
17.61 | 0.0074 | The rocking of the chlorine atoms, the rest of the complex is hardly displaced. |
| no | Form of the vibration | Frequency cm-1 | Intensity | Vibration description |
|---|---|---|---|---|
| 1 | .jpg){kind=spacer} |
5.04 | 0.0943 | The symmetric rocking of the eclipsed P-Cl bonds. The rest of the molecule (equatorial plane carbonlys) rock in a direction opposite to the trans ligands. |
| 2 | .jpg){kind=spacer} |
6.05 | 0.0 | The rocking of the P-Cl bonds in the phosphine ligands, but antisymmetrically wrt to each other (axial PCl3). The rest of the complex stays stationery. |
When a vibration has a very low frequency, this means that it is a very weak bond and would suggest that the bond breaks and reforms at room temperature. The Mo-P bonds are long and weak relative to the M-C bonds, I would expect the phosphine ligands to be labile, which means they hop on and off the metal complex, the Mo-P bond breaks and reforms at room temperature.
| no | Form of the vibration | Frequency cm-1 | Intensity | |
|---|---|---|---|---|
| 42 | Large antisymmetric stretch of the equatorial CO bonds and small antisymmetric stretch of axial CO bonds. | 1945.31 | 763.04 | |
| 43 | Large antisymmetric stretch of axial CO bonds and small antisymmetric stretch of equatorial CO bonds. | 1948.66 | 1498.24 | |
| 44 | Symmetric stretch of CO bonds, but antisymmetric with respect to axial and equatorial CO. | 1958.36 | 632.56 | |
| 45 | Totally symmetric stretch of all CO bonds. | 2023.31 | 597.98 |
| no | Form of the vibration | Frequency cm-1 | Intensity | |
|---|---|---|---|---|
| 42 | Antisymmetric stretch of two trans equatorial CO bonds. | 1950.29 | 1475.35 | |
| 43 | Antisymmetric stretch of two trans equatorial CO bonds. | 1950.92 | 1466.78 | |
| 44 | Symmetric stretch of trans equatorial CO bonds, but antisymmetric between cis CO bonds. | 1977.2 | 0.685 | |
| 45 | Totally symmetric stretch of all CO bonds. | 2030.99 | 3.81 |
The carbonyl frequencies of the trans isomer are generally larger in magnitude than the cis isomer carbonyl stretches. In the trans isomer the CO bond length is 1.173Å. In the cis isomer the equatorial CO bond length is 1.176Å and for axial is 1.173Å. A molecule is expected to have 3N-6 vibrations, in the case of the Mo(CO)4(PCl3)4 we would expect 75 different vibrations, however only 45 are observed. On the spectrum some of the vibrations overlap and appear as one peak, some of the vibrational frequencies (mainly the totally symmetric ones or ones with a total dipole moment of zero, therefore IR inactive) have intensities close to zero and do not appear on the spectrum.
Mini Project
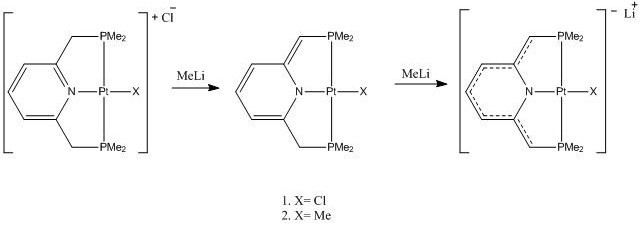
Cationic, neutral and anionic PtII PNP (PNP=2,6-bis-(di-tert-butylphosphinomethyl)pyridine) species were studied. The cationic species is aromatic, the complex was dearomatized by deprotonation at the PNP methylene group to give the neutral complex and the deprotonation of both PNP methylene groups to give an anionic complex. To do the DFT calculations, the tert-butyl groups on the PNP were replaced by methyl groups, I’m going to call this PNP*. Calculations were done where the X ligand is Cl and when it is Me. DOI:10.1021/ic902012z
The aim of my mini project was to observe how the bonding in the ring of PNP* ligand changes with the deprotonation and the effect of the deprotonation on the Pt-X bond.
The structure of the Pt-Cl cationic complex was drawn in Gaussview, the geometry of the molecule was then optimised. The method used was the DFT B3LYP and the basis set was LanL2MB, the additional key words “opt=loose” were added to the input file DOI:10042/to-3795 . When the optimisation was done, a second optimisation was run using the better basis set LanL2DZ and the additional key words used were “int=ultrafine scf=conver=9” DOI:10042/to-3796 . When the optimised geometry came back, a frequency calculation was run using the same method and basis set and all the frequencies came back positive showing that a minimum was reached DOI:10042/to-3810 . The population was also calculated to get the molecular orbitals of the complex DOI:10042/to-3811 . From the fully optimised geometry of the Pt-Cl cationic complex, all other variations of the complex were drawn then optimised and their frequencies calculated using the LanL2DZ basis set. All the frequencies were positive which shows that the optimised geometries are at a minimum energy.
| X ligand | Cationic | Neutral | Anionic |
|---|---|---|---|
| X is Cl |  |
 |
 |
| X is Me |  |
 |
 |
Optimisation files X=Cl, left to right DOI:10042/to-3795 DOI:10042/to-3809 DOI:10042/to-3808 Frequency files X=Cl, left to right DOI:10042/to-3810 DOI:10042/to-3945 DOI:10042/to-3944 Optimisation files X=Me, left to right DOI:10042/to-3943 DOI:10042/to-3942 DOI:10042/to-3941 Frequency files X=Me, left to right DOI:10042/to-3948 DOI:10042/to-3947 DOI:10042/to-3946
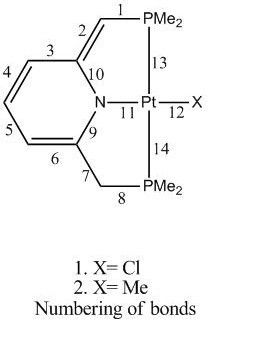
| no | Cl cation | Me cation | Cl neutral | Me neutral | Cl anion | Me anion |
|---|---|---|---|---|---|---|
| 1 | 1.90 | 1.90 | 1.81 | 1.81 | 1.79 | 1.79 |
| 2 | 1.52 | 1.52 | 1.40 | 1.40 | 1.42 | 1.42 |
| 3 | 1.40 | 1.41 | 1.45 | 1.45 | 1.44 | 1.43 |
| 4 | 1.40 | 1.40 | 1.38 | 1.38 | 1.40 | 1.40 |
| 5 | 1.40 | 1.40 | 1.40 | 1.43 | 1.40 | 1.40 |
| 6 | 1.40 | 1.41 | 1.39 | 1.39 | 1.44 | 1.44 |
| 7 | 1.52 | 1.52 | 1.52 | 1.52 | 1.42 | 1.42 |
| 8 | 1.90 | 1.90 | 1.89 | 1.90 | 1.79 | 1.79 |
| 9 | 1.38 | 1.38 | 1.39 | 1.38 | 1.41 | 1.40 |
| 10 | 1.38 | 1.37 | 1.42 | 1.41 | 1.41 | 1.40 |
| 11 | 2.07 | 2.18 | 2.06 | 2.16 | 2.06 | 2.14 |
| 12 | 2.40 | 2.08 | 2.43 | 2.09 | 2.47 | 2.10 |
| 13 | 2.36 | 2.36 | 2.36 | 2.36 | 2.37 | 2.37 |
| 14 | 2.36 | 2.36 | 2.37 | 2.36 | 2.37 | 2.37 |
The complexes have square planar geometries with the methylene/benzyl carbons and metal in the same plane as the ring. The two phosphines are above and below the pyridine plane for the cationci complexes. One phoshpine is in the plane of the ring and one above (or below)the ring in the neutral complexes and the anonic complexes are completely planar. The DFT calculations show that the neutral complex has a alternating single and double bonds, with and exocyclic C=C double bond to the deprotonated methylene. The anionic complex is a conjugated pi system comprising the ring carbons and exocyclic double bonds.
A normal C-C bond length is 1.54Å and C=C bond length is 1.34Å, C-N bond length is 1.45Å, C=N bond length is 1.21Å. In the cationic Pt-Cl complex, C-C bonds 3-6 are the same length (1.40 Å). This shows that the bonds have some double bond character, electron density is delocalised over the four bonds, this can be seen in MO 54 and 58 where the electron cloud isread over the bonds. C-C bonds 2 and 5, are 1.52Å which shows they have more single bond character. C-N bonds 9 and 10 are the same length 1.38Å and they show partial double bond character, this can be seen in the HOMO, where the elctron cloud is symmetrically distributed over the C-N-C bonds. This shows that charge is delocalised in the pyridinic ring (aromatic system) as the bonds show partial double bond character. The Pt-Cl bond length is 2.40Å, it can be seen from the HOMO that the elctron cloud on the Cl is large compared to that on the Pt, showing the electronegativity of the chloride.
In the neutral Pt-Cl complex, the bond lengths show that the system is not aromatic as there are discrete double and single bonds. C-C bond 2 (exocyclic double bond) shows partial double bond character (1.40Å), bond 3 shows more single bond character (1.45Å). However bond 4 shows the most double bond character, with a bond length of 1.38Å and appears as localised double bond on the graphical optimised structure. The C-N bond close to the exocyclic double bond is longer (1.42Å) than the one at the undeprotonated end (1.39Å).
The anionic Pt-Cl complex shows that there is delocalisation of charge over bonds 2-7 as the bond lengths show partial double bond character, ranging from 1.40-1.43Å. This agrees with the conjugated pi system that was observed in the literature. The Pt-N bond gets shorter as you go from the cationic (2.068Å), to the neutral (2.061Å) to the anionic (2.059Å). This shows that the nitrogen lone pair is less involved in the aromaticity of the ring with each deprotonation, therefore more of its electron density is shared with the metal. This is also shown by the increasing bond lengths of the C-N bonds (1.38Å to 1.41Å) and the decreasing Pt-N bonds. The Pt-Cl bonds get longer with each deprotonation from 2.40Å to 2.43Å to 2.47Å. The same trends are observed in the Pt –Me complexes.
The Pt-Cl and Pt-Me cationic complexes have similar bond lengths apart from the Pt-X and Pt-N bonds. Pt-Cl = 2.40Å, Pt-N=2.07Å and Pt-Me=2.08Å, Pt-N = 2.18Å. The chloride is electron withdrawing due to its high electronegativity and the methyl is slightly electron donating through inductive effects. The electron withdrawing nature of the chloride means that the metal is slightly electron deficient and thus forms a stronger bond to the slightly less electronegative nitrogen. The methyl pushes electron density towards the metal, making the Pt-Me bond stronger and the Pt-N bond longer compared to the chloride complex.