Rep:Mod:eun3
Module 3
Seongmin Eun CID:00549448
The Cope Rearrangement
Intronduction
The Cope rearrangement is an example of [3,3]-sigmatropic shift rearrangement. In this example, the rearrangement proceeds via a concerted migration of conjugate system in 1,5-hexadiene during which one of the σ bond is broken and new σ bond is formed. The below shows the mechanism of the Cope rearrangement:
It has been generally accepted that the Cope rearrangement of 1,5-hexadiene occurs via either a “chair” or “boat” transition state, where the former is energetically more favourable than the latter.
There are two possible transition states of this rearrangement, 'chair' and 'boat' transition state conformations. In this exercise, energy of every possible conformers of 1,5-hexadiene was first analysed to find out the most stable conformer at the HF/3-21G level of theory. Then, the boat and chair transition states were optimised and Intrinsic Reaction Coordinate (IRC) method was performed to bridge between the reactant conformer and the transition state.
Optimisation of the Reactants and Products
Possible conformations of 1,5-hexadiene were structured in Gaussian. There are two main streams of the conformers, "anti" and "gauche". In anti conformation, the two terminal carbon atoms are staggered to each other. In gauche conformation, the two terminal carbon atoms are partially starggered with 60o.
- HF/3-21G was used
This analysis reveals that the Gauche 3 conformer is most stable among the conformers. This could be explained in terms of stereoelectronic effect that stabilises the interaction between π-electrons of the C=C double bond and vinyl protons (C-H antibonding and C=C bonding orbital overlap). This is agreement with the statement written by Rocque et al [1]
Study of Anti 2 Conformer
In this exercise, Anti2 conformer was intensively studied with larger basis set B3LYP/6-31G.
| HF/ 3-21G | DFT/ B3LYP/ 6-31G* | |||||
| Structure |
https://wiki.ch.ic.ac.uk/wiki/index.php?title=Image:123ANTI2.mol |
https://wiki.ch.ic.ac.uk/wiki/index.php?title=Image:ANIT2_B3LYP_6-31.mol | ||||
| Point Group | Ci | Ci | ||||
| Energy/ Hartrees | -231.69254 | -234.61170 | ||||
| C1=C2 Bond Length/ Å | 1.32 | 1.33 | ||||
| C2-C3 Bond Length/ Å | 1.51 | 1.50 | ||||
| C3-C4 Bond Length/ Å | 1.55 | 1.55 | ||||
| C4-C5 Bond Length/ Å | 1.51 | 1.50 | ||||
| C5=C6 Bond Length/ Å | 1.32 | 1.33 | ||||
| C1-C2-C3-C4 Dihedral Angle/o | 114.7 | 118.7 | ||||
| C2-C3-C4-C5 Dihedral Angle/o | 180.0 | 180.0 | ||||
| C3-C4-C5-C6 Dihedral Angle/o | -114.7 | -118.7 |
The table above shows that the energy calculated by DFT was lower that that by HF. C=C double bond lengths were longer for DFT optimised structures and this could account for the lowered energy by relieving the steric repulsions. In addition, the dihedral angle between the terminal carbons was slightly larger for the DFT calculations.
Optimisation of Chair conformation
In this exercise, the TS structures of the Cope rearrangement are computationally optimised in two different ways.
A CH2CHCH2 allyl fragment was structured and optimised in Gaussian to HF/3-21G level of theory. This optimised fragment was duplicated on to the same file and they were orientated to look alike chair transition state as shown in the Appendix 2 and the distance between the terminal carbon atoms was set to be 2.2 angstroms.
The first method was to use to optimise the structure to a minimum/TS(Berny) and the force constant to be calculated once. The additional keywords Opt=NoEigen was inserted to prevent the calculation crashing from more than one imaginary frequency being found. The resulted geometry was the same as the structure shown in Appendix 2 as expected. There was an imaginary frequency at 818cm-1 and the animation of this corresponded to the bonds being formed and broken at the same time.
The second method consisted of two steps. The first step involved freezing the distance between the two pairs of terminal carbon atoms and perform an optimising calculation. These terminal atoms are responsible for making and breaking the bond. After optimisation, the freezing coordinates are changed to derivative and another optimisation took place. The resulted geometry was exactly the same ans the first method (Optimisation to TS(Berny)).
Comparison of Optimised "Chair" Transition States Using Different Approaches
| TS (Berny) Method | Frozen Coordinate Method | |
| Jmol | ||
| Image |  |

|
| Point Group | C2h | C2h |
| Energy/ Hartrees | -231.61932 | -231.61932 |
| Bond-Forming Length/ Å | 2.02 | 2.02 |
| Bond-Breaking Length/ Å | 2.02 | 2.02 |
| Imaginary Frequency/ cm-1 | -818 | -818 |
| Vibration at Imaginary Frequency |  |

|
| Log File | https://wiki.ch.ic.ac.uk/wiki/images/3/32/CHAIR_GUESS.LOG | https://wiki.ch.ic.ac.uk/wiki/images/6/65/CHAIR_REDUNDANT.LOG |
The main difference between the two methods is that the second step divides the process into two. First step is to do optimisation while freezing the terminal carbon atoms to find the transition state and second step to unfreeze the carbon atoms and relax the transition state into lowest potential energy. The second step would be favoured over when the fragments are large and complex.
Boat Transition State by QST2
Optimised Boat Transition State by QST2
| QST2 | |
| Jmol | |
| Image | 
|
| Point Group | C2v |
| Energy/ Hartrees | -231.60290 |
| Bond-Forming Length/ Å | 2.14 |
| Bond-Breaking Length/ Å | 2.14 |
| Imaginary Frequency/ cm-1 | -840 |
| Vibration at Imaginary Frequency | 
|
| Log File | https://wiki.ch.ic.ac.uk/wiki/images/1/13/BOAT_OPT_FREQ.LOG |
In this exercise, the boat transition structure was optimised using QST2 method. This method primarily analyses the reactant and the product from the input file and performs an interpolation calculation between the two structures to find the minimum energy transition state.
Anti2 structure was first optimised to HF3/3-21G level of theory and then a duplicate of this structure was made for a product structure. Then, the numbering of the atoms was altered carefully so that this corresponds to the product molecule with respect to that of original reactant.
However, these structures needed to undergo further modifications so that their C2-C3-C4 bond angle and C3-C4-C5 angle are 100o. This product structure was optimised to the transition state using Opt+Freq/TS(QST2). The results are as below. There was an imaginary frequency at -840cm-1 showing that the transition state has been successfully found. This vibration clearly shows the simultaneous formation of C-C bond while breaking of another C-C bond. The QST2 method was more challenging than the simple TS(Berny) method was QST2 required a precise numbering for the products and the correct starting geometries.
IRC
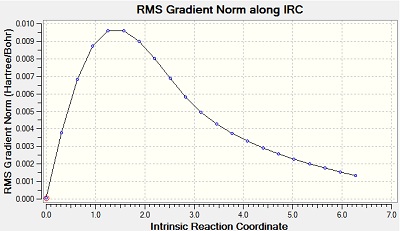
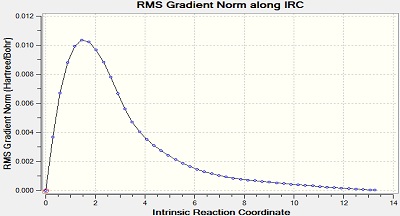
The Intrinsic Reactoin Coordinate(IRC) was calculated for both the chair and boat transition states by optimisation to TS Benry together with frozen coordinates method. This allows us to find the minium energy reaction pathway from a reactant to a product. Initially, IRC was calculated with 50 points along the pathway with the force constant computed only once. However, the RMS gradient did not become zero and this shows that method failed to reach the minimum energy. Another calculation was carried out with the force constant calculated at every point. In this trial, the RMS gradient reached zero meaning that the minimum geometry was found. This could have been achieved in a different way - by increasing the number of points (say to 100) so that the calculation continues to reach the minimum. The graphs and jmol views are available below:
| Force Constant Computation | Minimum Geometry Reached | Energy/a.u. | Total energy along IRC Path | Gradient along IRC Path | Minimum Structure | ||
| Once |
No | -231.68810 | 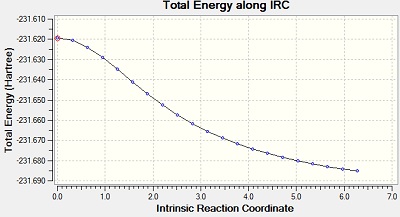
|
|
|||
| Always |
Yes | -231.69166 | 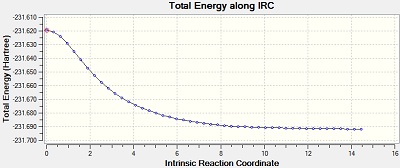
|
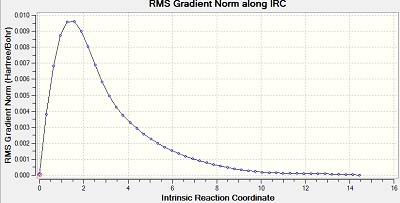
|
| Force Constant Computation | Minimum Geometry Reached | Energy/a.u. | Total energy along IRC Path | Gradient along IRC Path | Minimum Structure | ||
| Once |
No | -231.68810 | 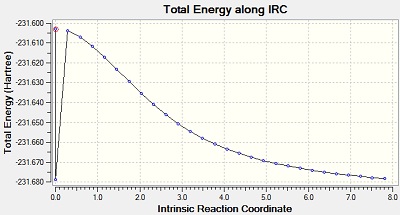
|
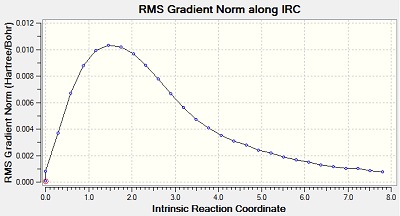
|
|||
| Always |
Yes | -231.69166 | 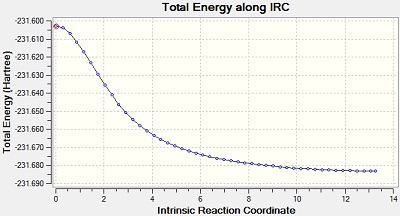
|
|
Energies
Summary of energies (in hartree)
A frequency calculation was performed to enable comparison of the calculated energy terms with the experimental values.
Frequency calculation allows the additional terms to be accounted and can be used to check if the conformer reached the minimum on the potential energy surface. To keep the consistency of the calculation, the same level of theory was applied. Information of the thermochemistry was extracted from the log file. This provided the potential energy at 0K and 298.15K.
We will optimise the transition states using the B3YLP/6-31G* level of theory to enable comparison to the HF/3-21G level. The results are summarised below and are consistent with those in Appendix 2:
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Chair TS | -231.61932 | -231.46671 | -231.46135 | -234.50545 | -234.36269 | -234.35677 |
| Boat TS | -231.60280 | -231.45093 | -231.44530 | -233.27600 | -233.13363 | -233.12756 |
| Reactant (anti2) | -231.69254 | -231.53954 | -231.53257 | -234.55970 | -234.41625 | -234.40895 |
*1 hartree = 627.509 kcal/mol
In this exercise, the transition states and activation energies were using B3LYP/6-31G* level of theory and compared with the HF/3-21G level. The results were consistent with Appendix 2 and summarised below:
Summary of activation energies (in kcal/mol)
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| 0 K | 298.15 K | 0 K | 298.15 K | 0 K | |
| ΔE (Chair) | 45.68 | 44.67 | 34.08 | 33.17 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.61 | 54.75 | 41.87 | 41.36 | 44.7 ± 2.0 |
It can be observed that the activation energy for the boat transition state is slightly higher in energy for both calculation methods, but they differed in the magnitude. For HF/3-21G, the boat TS energy was higher by 10 kcal/mol, whereas for the B3YLP/6-31G* was by 8 kcal/mol. This may be due to inherent computational errors of the calculations. The activation energy decreased by a very small amount as the temperature increased from 0K to 298.15K.
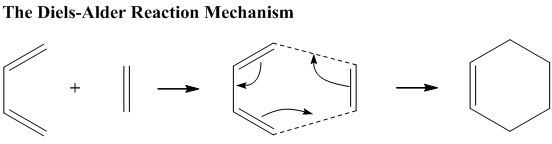
Diels-Alder Cycloaddition
Introduction
PartI
In the first part, the simplest Diels-Alder reaction of butadiene with ethene is studied. The mechanism is an example of[4+2] pericylic cycloaddition which involves the concerted formation of two σ-bonds to form a six-membered ring.
PartII
This is another example of cycloaddition reaction with 1,3-cyclohexadiene and maleic anhydride. In this part, MO was extensively studied to predict the relative stablility of exo and endo forms.
Part I
Butadiene and ethene undergo Diels-Alder reaction to form a six-membered ring. Both butadiene and ethene were optimized using AM1 semiempirical method and the HOMO and LUMO were visualised. The symmetry of each MO was studied as this determines whether the reaction is symmetrically allowed or not. In order to be symmetrically allowed, one should have Anti-Symmetric(AS) and the other with Symmetric(S). Also, using the knowledge that HOMO reacts with LUMO, The interaction of the MOs of butadiene and Ethene is favoured as they all result in AS+S.
Molecular Orbitals of Cis-Butadiene and Ethene
| Butadiene | Ethylene | |||
| HOMO | LUMO | HOMO | LUMO | |
| Molecular Orbital |  |
 |
 |

|
| Energy/ Hartrees | -0.34453 | 0.01793 | -0.38775 | 0.05284 |
| Symmetry | Anti-symmetric | Symmetric | Symmetric | Anti-symmetric |
The HOMO is a result of LUMO(Ethene) + HOMO(Butadiene) and LUMO is the result of HOMO(Ethene)+LUMO(Butadiene). Pericylic selection rule states that under thermal conditions, a reaction with 4n+2 pi-electrons forms a product by suprafacial stereochemistry. As it can be seen from this diagram, the two sigma bonds are made on the same face of the component pi systems and therefore it is an example of suprafacial interaction.
| HOMO | LUMO | |
|---|---|---|
| Molecular Orbital |  |

|
| Energy / a.u. | -0.32396 | 0.02320 |
| Symmetry | Antisymmetric | Symmetric |
The frequency analysis reveals that there is only one imaginary frequency at -956 cm-1 indicating that the traisition optimisation was successful.
The vibrating animation shows that the stretching of the two fragments is synchronous and this shows the two sigma bonds forming.
| Semi-empirical/AM1 optimize to Berny TS | ||||
|---|---|---|---|---|
| Optimized transition state |
| |||
| Energy /Hartrees | 0.11162 | |||
| C-C bond forming/breaking distance/ angstroms | 2.1 | |||
| Imaginary frequency / cm-1 | -956 | |||
| Animation of vibration |
|
Part II
| - | Exo | Endo | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Semi-empirical/AM1 | Imaginary Vibration | Semi-empirical/AM1 | Imaginary Vibration | |||||||
| Structure |
|
 |
|

| ||||||
| Energy /Hartrees | -0.05042 | -612.97931 | -0.05150 | -612.68340 | ||||||
| C-C bond forming distance /angstroms | 2.17 | 2.29 | 2.16 | 2.27 | ||||||
| Imaginary frequency /cm-1 | -812 | -448 | -806 | -447 | ||||||
- Log files were too large (2.5MB) so could not be uploaded.
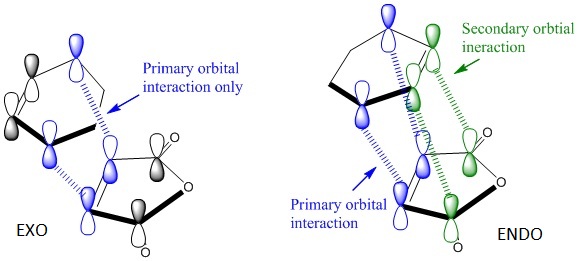
The distance between the carbonyl carbon in the maleic anhydride and the nearest CH2 is shorter for endo product than exo by 0.03Å. This can be interpreted as that endo product closer to the product structure and therefore more stabilised. In other words, endo- formation requires smaller activation energy and thus endo is a kinetic product. This is probably due to the secondary orbital interactions (SOI) which lowers the energy of endo- transition state while exo- has no SOI. SOI is illustrated below:
Marye Anne Fox et al[2] conducted many researches to study the balance between the steric effects and secondary orbital interactions (SOI). They defined SOI as the interaction of orbitals not involved in the primary bond forming overlaps. The SOI is often not strong enough to overwhelm the steric effects to form endo product if there is a presence of bulky groups. In the absence of bulky groups, like in this case, endo- form will be the dominant kinetic product. [3]
Referring to the MO diagrams below, the SOI can be seen for the endo form. The pi orbitals of the carbonyl carbons can communicate with the pi orbitals of the diene and stabilise the transition state. However, if there is a bulky group on either side, the distance of the two SOI p-orbitals will be too large and will have negligible effect on TS energy.
| Exo | Endo | ||
|---|---|---|---|
| HOMO | LUMO | HOMO | LUMO |
 |
 |
 |

|
| Antisymmetric | Antisymmetric | Antisymmetric | Antisymmetric |
Reference
- ↑ B. G. Rocque, J. M. Gonzales, H. F. Schaefer III, Molecular Phy., 2002, 100, 441 - 446DOI:10.1080/00268970110081412
- ↑ Marye Anne Fox, Raul Cardona, Nicoline J. Kiwiet DOI:10.1021/jo00384a016
- ↑ W.C. Herndon, C.R. Grayson, J.M. Manion, J. Am. Chem. Soc.., 2002, 124, 1130: DOI:10.1021/jo01278a003