Rep:Mod:eun
Computational Lab:Module 2
Seongmin Eun
CID:00549448
Notes on accuracy
- Energy will have an error up to 10kJ/mol which are 2.3x1021 hartrees.
- Dipole moment will only be accurate to 2 decimal places, i.e. 0.01 Deby.
- All frequencies are represented in wavenumbers with no decimal places.
- Frequency will have an error around 10%.
- Intensities are rounded up to the nearest whole integer.
- Bond distances are accurate to 0.01Å
BH3
Optimising a Molecule of BH3
In this calculation, the basis set was set to be 3-21G. Although 3-21G is a small basis set, the optimization is still expected to be fine as BH3 is a symmetric small molecule.
The log file of optimized BH3: https://wiki.ch.ic.ac.uk/wiki/index.php?title=Image:Eun_BH3_OPT.LOG
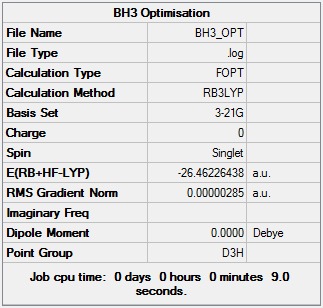
Optimisation Summary of BH3:
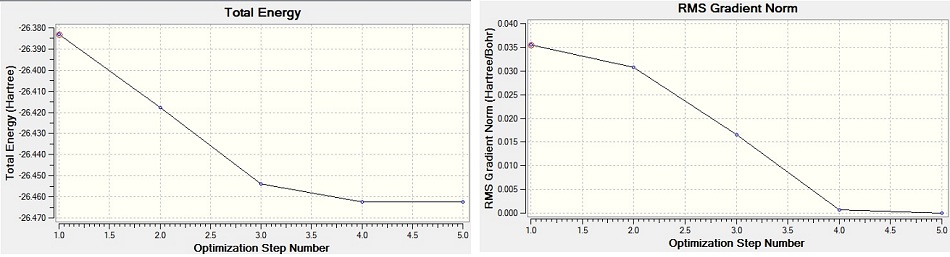
Energy and gradient graph were extracted from the output file of BH3 optimization (see below): The left graph illustrates the energy of molecule at each stage of optimisation and the right graph shows the gradient of the energy against optimization steps. The gradient in this case is defined as the rate of change of the energy with respect to the number of optimizations carried out. The input molecule is modified according to the repulsive and attractive forces. The minimum energy of geometry is approached by step by step decrease in energy until the gradient becomes zero.
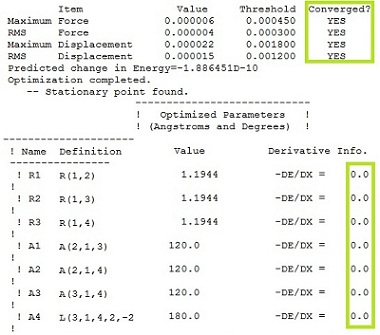
Gradient being zero proves that the optimization was complete:
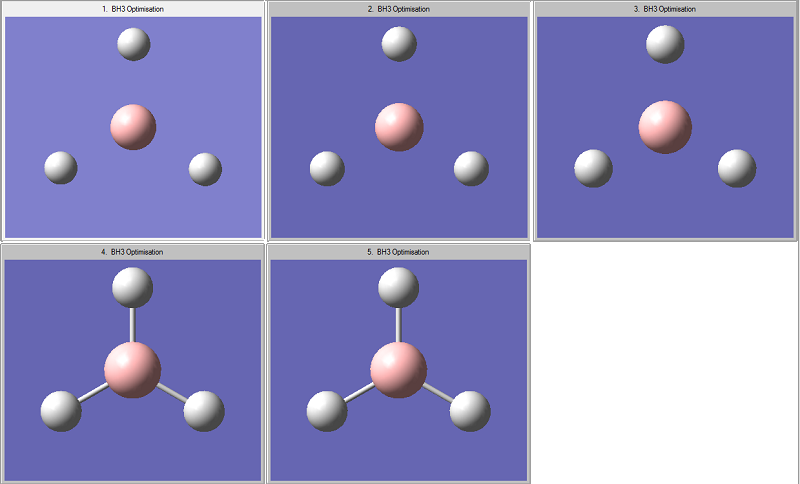
The picture below shows the step by step optimisation:
| Property | Value |
|---|---|
| B-H bond length (Å) | 1.192 |
| H-B-H bond angle (o) | 120 |
| Calculation method | B3LYP |
| Basis set | 3-21G |
| Final energy (a.u.) | -26.467 |
| Gradient (a.u.) | 0.000207 |
| Point group | D3h |
The bond length is very closely to the literature value, which is 1.21Å and the H-B-H bond angle is 120.1o.
Pseudo-Potentials and Basis Sets
Original File can be found here: DOI:10042/to-7533
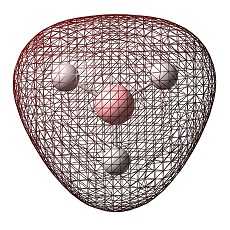
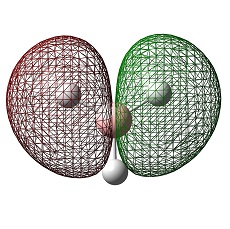
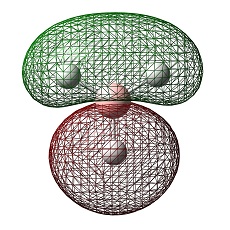
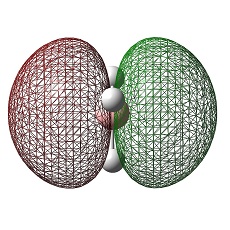
Molecular Orbitals of BH3
The HOMO was a degenerate e' and LUMO was a non-bonding pz on the boron atom. The LUMO was relatively low in energy as it was non-bonding pz of the electropositive boron atom. This low lying LUMO imparts the BH3 to be a good electron acceptor and therefore a good Lewis acid.
The main difference comes from the fact that in the LCAO MO diagram, each AO is overlapped one onto the other. On the other hand, in the real molecular orbitals, each AO is smoothly combined and electron density is dispersed over the molecular orbitals.
(LCAO is given by the formula Ψ Γ=N(c1 Ψ 1 +c2 Ψ 2...cn Ψ n)= NΣ ci Ψ i where Γ is the symmetry label, N is the normalisation criteria, the c is the normalisation constant, and i is an index.)
 |
 |
 MO 3 |
 MO 4 |
 MO 5 |
 MO 6 |
 MO 7 |
 MO 8 |
Frequency Analysis of BH3
This is the summary of BH3:
Below shows that animation of each vibration mode:
|
|
Vibration 3
|
Vibration 4
|
Vibration 5
|
Vibration 6
|
Optimised BH3 was then further analysed by its vibrational modes and frequency. BH3 has 6 vibrational modes which is accordance with the outcome of the non-linear vibrational modes formula 3N-6 (N=4). BH3 has a2' ', e', e', e' ', e' ', a1' '. Although the BH3 has 6 vibrational modes, they are not all infrared active. To be infrared active, a vibrational mode should consequence a change in dipole moment. In other words, a fully symmetric vibration would not result a change in dipole and thus it's IR inactive. a1' is a fully symmetric vibration and therefore it will not show up in the IR spectrum. a2' ' vibrational mode accompanies a change in dipole and the peak is observed on the IR spectrum. Each of e' and e' ' has two degenerate(=same frequency) vibrational modes so there are only two peaks are observed.
'Low Frequencies' are the motions that are related to the centre of mass. They are typically much smaller than those of normal vibrational modes.
Kaldor [1] reported peaks at 1125cm-1, 1604cm-1, 2808cm-1 and they are reasonably close to the calculated values as the dimerisation of BH3 to B2H6 is facile and changed the literature values. Also, the accuracy would have been better if larger basis set was used.
NBO Analysis for BH3
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.33126 1.99904 2.66970 0.00000 4.66874
H 2 -0.11042 0.00000 1.11010 0.00032 1.11042
H 3 -0.11042 0.00000 1.11010 0.00032 1.11042
H 4 -0.11042 0.00000 1.11010 0.00032 1.11042
=======================================================================
* Total * 0.00000 1.99904 6.00000 0.00097 8.00000
This summarises the variety of information of the analysis cycle. This tells that NBO search was carried out only once, and the resulted populations for Lewis and Non-Lewis are 7.99457 and 0.00543 respectively. The number of core (CR) was found to be one; 2-center bond (BD) was three, and there were no 3-center bond (3C) and no lone pair. The maximum deviation (Dev) of any formal bond order for the structure from a nominal estimate (NAO Wiberg bond index) is zero. The Lewis structure is acceptable since all orbitals for the formal Lewis structure is greater than the occupancy threshold (default=1.90 electrons).
NATURAL BOND ORBITAL ANALYSIS:
Occupancies Lewis Structure Low High
Occ. ------------------- ----------------- occ occ
Cycle Thresh. Lewis Non-Lewis CR BD 3C LP (L) (NL) Dev
=============================================================================
1(1) 1.90 7.99457 0.00543 1 3 0 0 0 0 0.00
-----------------------------------------------------------------------------
Structure accepted: No low occupancy Lewis orbitals
--------------------------------------------------------
Core 1.99904 ( 99.952% of 2)
Valence Lewis 5.99553 ( 99.926% of 6)
================== ============================
Total Lewis 7.99457 ( 99.932% of 8)
-----------------------------------------------------
Valence non-Lewis 0.00447 ( 0.056% of 8)
Rydberg non-Lewis 0.00097 ( 0.012% of 8)
================== ============================
Total non-Lewis 0.00543 ( 0.068% of 8)
--------------------------------------------------------
The above table describes the general quality of the natural Lewis structure in terms of the percentage of the total electron density. In this BH3, it’s around 99.9%. The table also shows the relative importance of the valence non-Lewis orbitals (i.e., the three valence antibonds, NBO 13-15, see below) relative to the extra-valence orbitals (the seven Rydberg NBOs 6-12) from the localised Lewis structure model.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99851) BD ( 1) B 1 - H 2
( 44.49%) 0.6670* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 55.51%) 0.7451* H 2 s(100.00%)
1.0000 0.0000
2. (1.99851) BD ( 1) B 1 - H 3
( 44.49%) 0.6670* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.51%) 0.7451* H 3 s(100.00%)
1.0000 0.0000
3. (1.99851) BD ( 1) B 1 - H 4
( 44.49%) 0.6670* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.51%) 0.7451* H 4 s(100.00%)
1.0000 0.0000
4. (1.99904) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
6. (0.00000) RY*( 1) B 1 s( 0.00%)p 1.00(100.00%)
7. (0.00000) RY*( 2) B 1 s( 0.00%)p 1.00(100.00%)
8. (0.00000) RY*( 3) B 1 s( 0.00%)p 1.00(100.00%)
9. (0.00000) RY*( 4) B 1 s( 0.00%)p 1.00(100.00%)
10. (0.00032) RY*( 1) H 2 s(100.00%)
0.0000 1.0000
11. (0.00032) RY*( 1) H 3 s(100.00%)
0.0000 1.0000
12. (0.00032) RY*( 1) H 4 s(100.00%)
0.0000 1.0000
13. (0.00149) BD*( 1) B 1 - H 2
( 55.51%) 0.7451* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 44.49%) -0.6670* H 2 s(100.00%)
1.0000 0.0000
14. (0.00149) BD*( 1) B 1 - H 3
( 55.51%) 0.7451* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 44.49%) -0.6670* H 3 s(100.00%)
1.0000 0.0000
15. (0.00149) BD*( 1) B 1 - H 4
( 55.51%) 0.7451* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 44.49%) -0.6670* H 4 s(100.00%)
1.0000 0.0000
The first column of above indicates the occupancy (0-2 electrons) and original label of the NBO.
(RY*=1-center Rydberg, BD*=2-center antibond, Starred=Lewis NBO, Unstarred=Non-Lewis NBO)
The next column shows the natural atomic hybrids of the NBO. This is represented with the square of the polarization coefficients of the NBO. The hybrid label tells that BH bond is sp2 hybridized (i.e. 33% s-character, 67% p-character). For instance, the B-H bonds (NBO 1-3) and antibonds (NBO 13-15) are described as below (Threshold = 0.5kcal/mol, which means any energy smaller than 0.5kcal/mol is not displayed):
Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
within unit 1
4. CR ( 1) B 1 / 10. RY*( 1) H 2 1.51 7.55 0.095
4. CR ( 1) B 1 / 11. RY*( 1) H 3 1.51 7.55 0.095
4. CR ( 1) B 1 / 12. RY*( 1) H 4 1.51 7.55 0.095
The next demonstrates the donor-acceptor (bond-antibond) interactions in the NBO basis:
SBH =0.6670(sp2)B + 0.7151(sp2)H
SBH*=0.7451(sp2)B – 0.6670(sp2)H
This analysis examines all possible interactions of filled (donor) Lewi-type NBOs with empty (acceptor) non-Lewis NBOs. Then, 2nd order perturbation theory is introduced to estimate their energetic importance. Donation of localised NBOs of the idealised Lewis structure into the empty non-Lewis orbitals proceeds via those interactions. The 0th order Lewis structure is deviated from the idealised Lewis structure by these delocalisation corrections. The E(2) associated with the delocalisation is calculated by the formula below:
Natural Bond Orbitals (Summary):
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (H3B)
1. BD ( 1) B 1 - H 2 1.99851 -0.43697
2. BD ( 1) B 1 - H 3 1.99851 -0.43697
3. BD ( 1) B 1 - H 4 1.99851 -0.43697
4. CR ( 1) B 1 1.99904 -6.64515 10(v),11(v),12(v)
5. LP*( 1) B 1 0.00000 0.67699
6. RY*( 1) B 1 0.00000 0.37185
7. RY*( 2) B 1 0.00000 0.37185
8. RY*( 3) B 1 0.00000 -0.04544
9. RY*( 4) B 1 0.00000 0.43447
10. RY*( 1) H 2 0.00032 0.90032
11. RY*( 1) H 3 0.00032 0.90032
12. RY*( 1) H 4 0.00032 0.90032
13. BD*( 1) B 1 - H 2 0.00149 0.41092
14. BD*( 1) B 1 - H 3 0.00149 0.41092
15. BD*( 1) B 1 - H 4 0.00149 0.41092
-------------------------------
Total Lewis 7.99457 ( 99.9321%)
Valence non-Lewis 0.00447 ( 0.0559%)
Rydberg non-Lewis 0.00097 ( 0.0121%)
-------------------------------
Total unit 1 8.00000 (100.0000%)
Charge unit 1 0.00000
1|1|UNPC-UNK|SP|RB3LYP|3-21G|B1H3|PCUSER|10-Mar-2011|0||# rb3lyp/3-21g
pop=(nbo,full) geom=connectivity||BH3 Optimisation||0,1|B,0,0.,0.,0.|
H,0,0.,1.19435287,0.|H,0,1.03433993,-0.59717644,0.|H,0,-1.03433993,-0.
59717644,0.||Version=IA32W-G03RevE.01|State=1-A1'|HF=-26.4622633|RMSD=
4.079e-007|Thermal=0.|Dipole=0.,0.,0.|PG=D03H [O(B1),3C2(H1)]||@
The table gives an overview of the relationships between the donor and acceptor NBO and their topological relationships. In this case, the acceptor orbitals are attached to an adjacent atom and therefore they are all in vicinal(v) positions. The summary at the bottom shows that 99.93% of the electron density is described in Lewis NBOs 1-4 and 0.07% of the electron density is described in non-Lewis NBOs 5-15.
TlBr3
The molecule TlBr3 was created using Gaussview, and the symmetry was set to D3h, increasing the tolerance to 0.0001 to ensure the MO and Vibrational calculations to be run later are correct. The optimisation was run using the B3LYP method, with the basis set set to LanL2DZ. Log File:https://wiki.ch.ic.ac.uk/wiki/images/d/d1/TLBR3_OPTIMISATION.LOG
| File Type | .log |
| Calculation Type | OPT |
| Calculation method | RB3LYP |
| Basis set | LANL2DZ |
| Final energy (a.u.) | -91.29 |
| Gradient (a.u.) | 0.00000072 |
| Point group | D3h |
Tl-Br bond length: 2.651 Angstroms
Br-Tl-Br bond angle: 120o
This is close to the literature[2] bond length (2.512 Angstroms) but the accuracy could be improved if a larger basis set is employed.
Vibrational Analysis on TlBr3
The vibrational and frequency analysis involve two main purposes here. Firstly, this analysis can be a measure of if the geometry optimisation was carried out successfully with correct structure. Secondly, the frequency analysis is a useful tool to judge if the optimised structure is actually the minimum. Frequency analysis usually employs the maxima and minima (first derivative) calculated from the optimisation in order to calculate the second derivative and see if the outcome is positive or negative. A positive value means the point is at the minimum place and a negative value means the point is at the maximum place (i.e. transition state). File:DOI:10042/to-7896
Same method as optimisation procedure was used in order to keep the consistency.
| File Type | .log |
| Calculation Type | FREQ |
| Calculation method | RB3LYP |
| Basis set | LANL2DZ |
| Final energy (a.u.) | -91.29 |
| Gradient (a.u.) | 0.00000072 |
| Point group | D3h |
The energy is the same as the optimised energy, i.e. the optimisation was successful and correct.
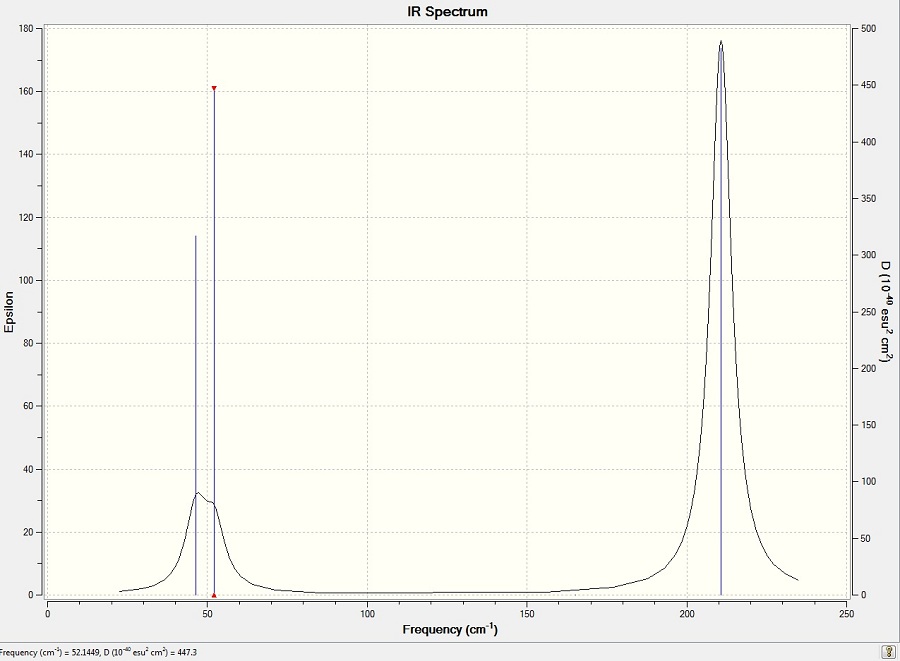
'Low frequencies' are taken from the log file. Their small magnitudes indicate that the calculation was successful.
- Low frequencies= 3.4214 -0.0025 -0.0004 0.0017 3.9368 3.9368
Gaussview does not recognise a bond which exceeds its bond length limit. Any greater than the bond length limit, the Gaussview thinks the two atoms are to distant to form a localised bond.
Then what is a bond? In short, a chemical bond is the favourable interaction between two atoms, induced by electrons. Normally, bondings lower the overall potential energy and therefore stabilise the system.
| Mode # | Vibration | Freq./ cm-1 | Intensity | Symmetry D3h point group | |||
| 1 |
Vibration 1
|
46 | 4 | E' | |||
| 2 |
Vibration 2
|
46 | 4 | E' | |||
| 3 |
Vibration 3
|
52 | 6 | A2' | |||
| 4 |
Vibration 4
|
165 | 0 | A1' | |||
| 5 |
Vibration 5
|
211 | 25 | E' | |||
| 6 |
Vibration 6
|
211 | 25 | E' |
Isomers of Mo(CO)4L2
This section is to model cis- and trans- Mo(CO)4PCl3 and compare their energies and vibrational modes.
Optimised structures of the cis and trans complexes and their relative energy
First, cis- and trans- Mo(CO)4PCl3 molecules were constructed on Gaussian View by B3LYP method. Then the chlorides in the structures were modified into a different orientations and another optimisation was carried out with LANL2MB. This basis set achieves a better accuracy than B3LYP as this only includes the minimal basis set for the phosphorus atom which is able to form a hypervalent form by using its low lying d-orbitals. Cis:DOI:10042/to-7897 TransDOI:10042/to-7898
The cis and trans isomers possess different symmetry point groups. Plus, their bond length of Mo-C and Mo-P are different. Mo-P bond is longer in cis isomer. The difference in bond length are thought to be due to steric repulsion of large chloride atom.
Thermodynamic Approach
The trans isomer was in lower energy than cis isomer by 3kJ/mol, which is very small and lies within the error of the method. The reason for cis isomer to be in higher energy would be due to the unfavourable steric repulstion between two bulky PCl3
Vibrational Anaylsis
They both featured 45 vibrational modes and this is the same as calculated from 3N-6 (N=17). Only the carbonyl stretches were investigated as they are the ones that can differentiate the isomers. Cis- isomer has a C2V symmetry and shows 4 active carbonyl stretching modes, whilst the trans isomer has a D4h symmetry and shows only 1 active carbonyl vibrational modes (actually 2 but merged into 1). Cis DOI:10042/to-7899 , TransDOI:10042/to-7900
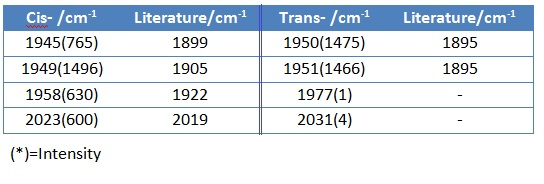The calculated values were reasonably close to the literature values.
The cis isomer features symmetric stretches for trans- pair of carbonyls and asymmetric stretches for cis- pair of carbonyls. This proves the existence of four vibrational modes on IR spectrum. Also, trans pairs of carbonyl groups have greater force constants than cis pairs, the highest frequency band at 2020cm-1 takes place in cis isomer with A1 symmetry.
In the trans isomer, there are two vibrational modes which are IR active. The trans isomer shows 1950-1 which is exhibited by the asymmetric stretching of two trans carbonyl pairs and has a Eu symmetry. Such asymmetric vibrations for cis isomer is at 1945cm-1.
Results for last year’s experiment (5 S Identification of stereochemical isomers of Mo(CO)4L2 by infrared spectroscopy) as well as literature data are presented below. For both complexes the computed IR stretching frequencies for Mo(CO)4(PCl3)2 correspond quite well to those reported in literature for Mo(CO)4(PPh3)2. Overall slightly higher stretching frequencies are computed here due to the P-Cl force constant being higher than P-R one. Further error is due to the medium level accuracy of the method and basis set.
Cis- Vibration 1
|
Cis- Vibration 2
|
Cis- Vibration 3
|
No negative frequencies were observed in both of the isomers. Low frequencies were displayed which correspond to rearrangements of the ligand groups about the Mo centre. This suggests the cis-trans isomerisation is thermally accessible at room tempearture. The first three vibrational modes (see above) of the cis isomer shows the partial rotations of the carbonyl and PCl3 groups to form a trans isomer. This particular isomerisation can be explained by 'Bailar-twist isomerisation'.
Trans- Vibration 42
|
Trans- Vibration 43
|
Trans- Vibration 44
|
Trans- Vibration 45
|
Cis- Vibration 42
|
Cis- Vibration 43
|
Cis- Vibration 44
|
Cis- Vibration 45
|
Mini Project
Introduction
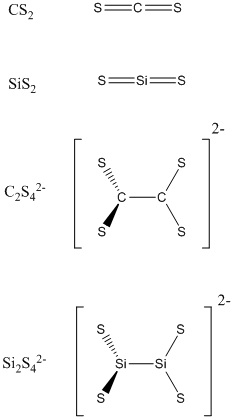
In this mini project, four molecules were intensively investigated.
The disulfides of Group 4 show the gradation in properties that might be expected to accompany the increasingly metallic character of the elements.
Carbon disulfide is made by heating charcoal with sulphur at 1200K. It is an excellent solvent which is used in the production of cellophane and rayon. Carbon disulfie is insoluble in water, but to some extent thermodynamically unstable with respect to hydrolysis to CO2 and H2S.
Silicon disulfide is prepared by heating silicon in sulfur vapour and forms dimeric chain. Interestingly, SiS2 shows no parallels with SiO2; SiS2 is instantly hydrolysed.
In addition, when carbon disulfide reacts with hydrochloric acid, [C2S4]2- is formed, whereas no such silicon compound was yet reported.
This project has two main purposes.
First, why does CS2 exists as a stable monomer but why SiS2 should polymerise?
Second, why does C2S42- forms but why Si2S42- cannot form?
(Since polymeric structure cannot be used in calculation, its dimeric anions were studied)
The questions were approached in a various ways. Optimisation was performed in prior to any other calculations. Then the molecular orbitals and frequency analysis were done.
Energy
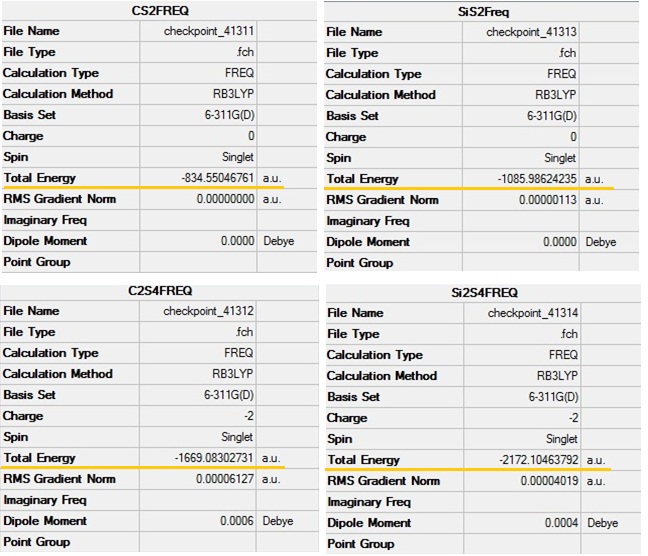
This is a summary of optimised compounds.
It can be noticed that both CS2 and SiS2 are lower in energy when they are in the form of dimeric anions.
Surprisingly, there are no great differences in energy between the species.
Optimised CS2:DOI:10042/to-7901
SiS2DOI:10042/to-7902
C2S4DOI:10042/to-7903
Si2S4DOI:10042/to-7904
Molecular Orbitals
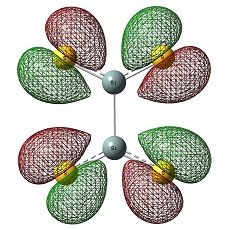
The two molecules do not feature a great difference other than that the LUMO of SiS2 is place in d-orbital.:
 |
 |
 CS2 LUMO20 |
 |
 |
 SiS2 LUMO24 |
Again, the HOMO and LUMO of each compound look very similar:
 C2S4-2 HOMO39 |
 C2S4-2 LUMO40 |
 Si2S4-2 HOMO47 |
 Si2S4-2 LUMO48 |
Therefore, molecular orbitals cannot be a clear guide to explain the stability of each compound.
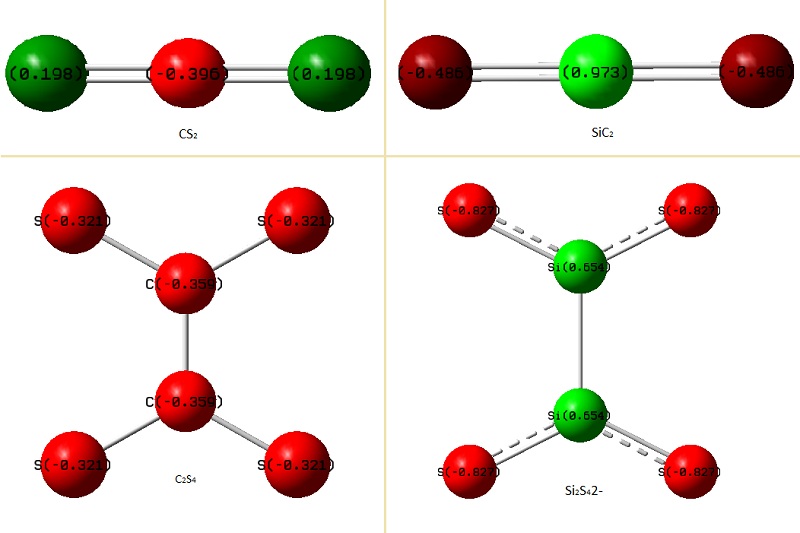
Natural Bonding Orbitals
This is the result of NBO calculation:
The red colour represents that the atom is negatively charged.
The green colour means it's positively charged.
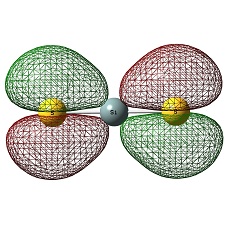
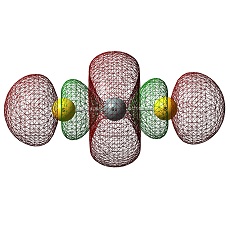
CS2 and SiS2
It is distinct that C atom is negatively charged in CS2 whilst Si is postively charged in SiS2.
This trend can be interpreted in terms of electropositivity- Si is more electropositive than C.
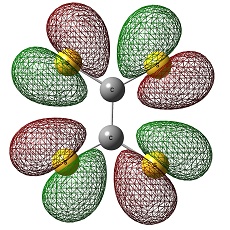
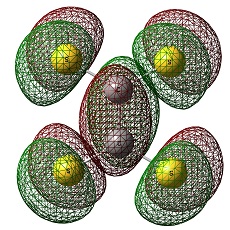
C2S42- and Si2S42-
Also, the most important information it gives is that the the carbon atom in C2S4 is negatively charged whilst in Si2S4, the negative charges are all distributed on the sulphur atoms, imparting Si atom to be positively charged. The reason for the carbon atoms to be negatively charged would be due to the small size of carbon atoms and therefore the large sulphur electrons are smeared out into it. On the other hand, Si atoms has available empty d-orbitals which Si atoms can use to disperse the electrons along the S-Si-S bond and avoids being negatively charged.
It can be concluded that polymeric structure is much more favourable for Si2S42-. Also, it can be seen from the log files that eight of electrons in Si2S42- are actually in antibonding manner. When this anion comes to form a neutral polymeric compound with positively charged species, this will be quite thermodynamically favourable.
Frequency Analysis
CS2:DOI:10042/to-7905 SiS2DOI:10042/to-7906 C2S4DOI:10042/to-7907 Si2S4DOI:10042/to-7908
Frequency Analysis was not quite useful here. There were no relevant references found.
Vibration 1 CS2
|
Vibration 2 CS2
|
Vibration 3 CS2
|
Vibration 4 CS2
|
Vibration 1 SiS2
|
Vibration 2 SiS2
|
Vibration 3 SiS2
|
Vibration 4 SiS2
|
Vibration 1 C2S4
|
Vibration 2 C2S4
|
Vibration 3 C2S4
|
Vibration 4 C2S4
|
Vibration 5 C2S4
|
Vibration 6 C2S4
|
Vibration 7 C2S4
|
Vibration 8 C2S4
|
Vibration 9 C2S4
|
Vibration 10 C2S4
|
Vibration 11 C2S4
|
Vibration 12 C2S4
|
Vibration 1 Si2S4
|
Vibration 2 Si2S4
|
Vibration 3 Si2S4
|
Vibration 4 Si2S4
|
Vibration 5 Si2S4
|
Vibration 6
|
Vibration 7 Si2S4
|
Vibration 8 Si2S4
|
Vibration 9 Si2S4
|
Vibration 10 Si2S4
|
Vibration 11 Si2S4
|
Vibration 12 Si2S4
|
References
- ↑ A. Kaldor and R. F. Porter, J. Am. Chem. Soc., 93 (1971) 2140 Template:DOI:10.1021/ja00738a008
- ↑ A.M. Glaser, J. and J ohansson, G. Caminiti, Acta Chem. Scand. A 35 125 639
- ↑ ELmer C. Alyea and Shuquan Song, Inorg. Chem., 1995 34, 3864-3873 DOI:10.1021/ic00119a006
- ↑ F. A. Cotton, Inorg. Chem., 1964, 3, 702-711 DOI:10.1021/ic50015a024