Rep:Mod:euhrfwfjhsd
3rd Year Computational Lab
Module 2: Inorganic
Day 1: The investigation of small molecules using Gaussian
BCl3
Gaussian was used in conjunction with gaussview to optimise the geometry of a BCl3 molecule using a DFT calculation with a B3LYP electron repulsion adjustment and a medium complexity basis set, LanL2MB; heavy and light atoms are treated differently. The more involved D95V basis set is used on first row atoms and the more facile Los Alamos ECP is used on the heavier elements.
The optimised molecule was found to have a B-Cl length of 1.86592Å and a Cl-B-Cl bond angle of 120°.
The file type was a .mol and the calculation type was FOPT. The method used was RB3LYP, and the basis set was LANL2MB. The final energy was calculated to be -69.43928112 A.U. and the dipole moment was 0.000 Debye. The point group was found to be D3h and the calculation took 14 seconds.
Phosgene; COCl2
The molecule was optimised as before and the results are displayed below.
Center Atomic Atomic Coordinates (Angstroms) Number Number Type X Y Z --------------------------------------------------------------------- 1 6 0 0.000000 0.615345 0.000000 2 8 0 -0.000013 1.829378 0.000000 3 17 0 -1.591600 -0.539074 0.000000 4 17 0 1.591606 -0.538990 0.000000 --------------------------------------------------------------------- Rotational constants (GHZ): 6.4476233 2.8525700 1.9776252
The C=O bond length was found to be 1.21403Å and the C-Cl bond lengths were found to be 1.96618Å. This distance is so long that gaussview doesn’t even display them as formal bonds. The reason for the length of these bonds is related to the extreme electrophillicity of the carbon the fact that Cl is an exceedingly good leaving group. All these lead to the bond being very weak and hence long.
The Cl-C-Cl bond angle is 108.09384° and the O-C-Cl bond angle is 125.95351°.
The calculation method was RB3LYP and the basis set used was LANL2MB. The final energy calculated was -141.67 a.u. and the dipole moment was. 1.7184 debye. The point group was calculated to be CS and the calculation took 39 seconds.
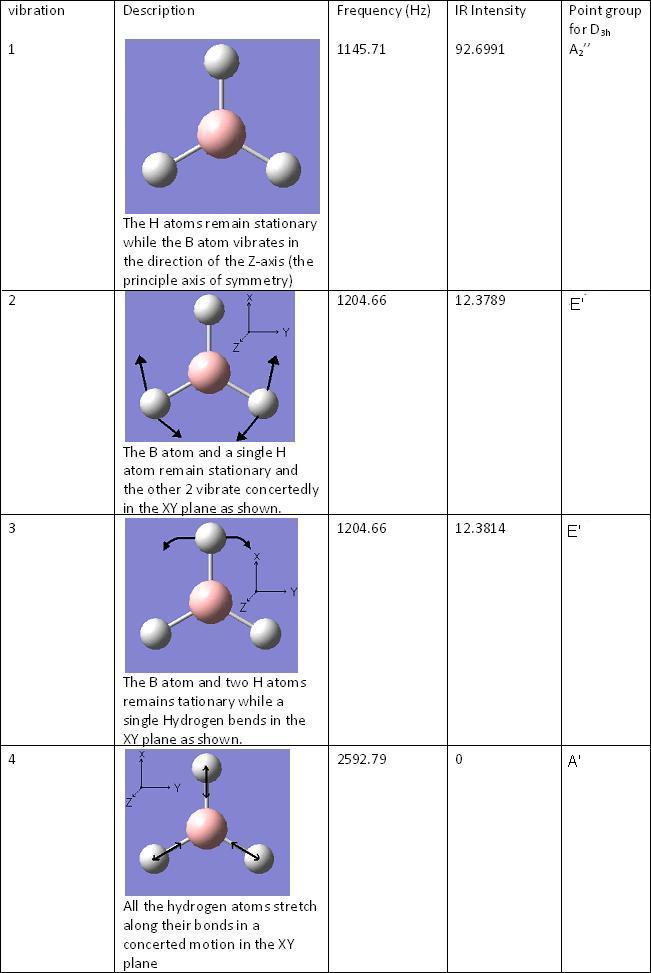
BH3 Vibrations
The vibrational energies were calculated for BH3 and the optimised energy was found to be -26.462 a.u.
Predicted MO Diagram
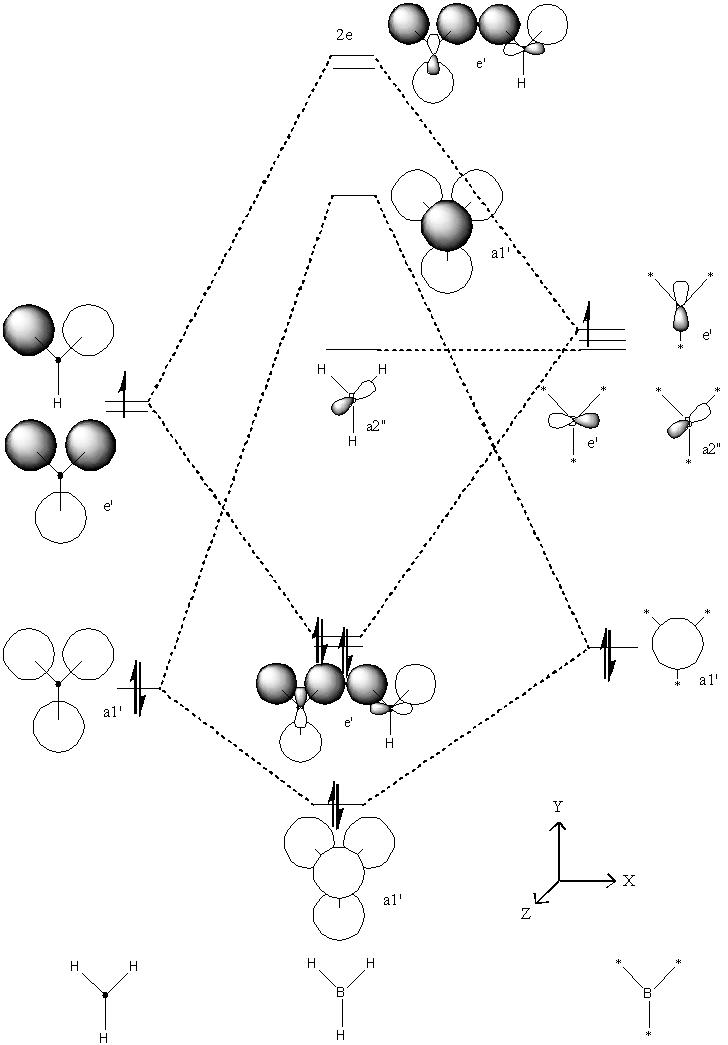
Comparison of the molecular orbitals calculated using computational methods and those by LCAO
MO 1
This MO has no equivalent on my MO diagram because I only use to show the valence orbital interactions (I neglected Boron’s 1S2 orbital). This is because the orbital is too low in energy to interact so will not affect the stability of the bond. If I had chosen to show the orbital I would have drawn an unhybridised S orbital centred on the boron atom. Consequently I can say LCAO was a very accurate method in predicting the shape of this orbital.
MO 2
Both molecules show a continuous array of electron density across all 4 atoms with no nodes. The computed orbital shows a smoother transition between the different atomic orbitals but on the whole is very similar to the LCAO orbital.
MO 3
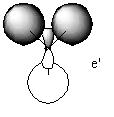
Both techniques show a molecular orbital with a single node and the same symmetry. The only difference between the two is that the computational method has smoothed the atomic orbitals that make up the molecular orbital together.
MO 4 (HOMO)
Both techniques give a MO with the same distribution of electron density (noticeable in its absence from one of the hydrogens). Again the only real difference is the smoothing of the atomic orbitals performed by the computational method.
MO 5 (LUMO)
Both techniques give almost identical representations of the Molecular orbitals.
Summary
Qualitative MO methods are extremely accurate at predicting the general shapes and symmetries of the MO’s but cannot accurately reveal the actual sizes and energies of the orbitals. The shapes cannot be predicted more accurately than the overlay of the atomic orbitals that contribute most towards them but in most cases this is a remarkably accurate approximation.
Day 2: The Investigation of a Transition Metal Complex
A Complex of Mo(CO)4(P(CH3)3)2 was built in Gaussview and then optimised using B3LYP method and a an approximate basis set,LANL2MB. The convergence criteria was set to be loose. An approximate method is used for this intital optimisation because it takes significantly less time to perform a series of optimisations with progressively more rigorous methods and basis sets than it is to run an calculation with tight optimisation criteria initially.
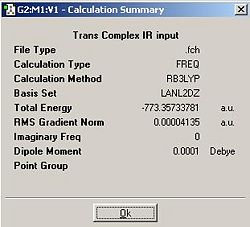
After the this initial optimisation was complete the out put was submitted to a more weighty optimisation,B3LYP method with the LANL2DZ basis set as well as int=ultrafine in the addition keywords. The results of these optimisation are located below.
Optimised Trans Complex Location http://hdl.handle.net/10042/to-1028
Optimised Cis Complex Location http://hdl.handle.net/10042/to-1029
Trans Complex IR Location http://hdl.handle.net/10042/to-1030
Cis Complex IR Location (IT staff contacted: optimised correctly but could not be submitted to depository. As the wiki instruction explicitly forbid linking to the .fchk file directly I suggest you contact me if you require the file and I shall email the .fchk file as soon as possible)
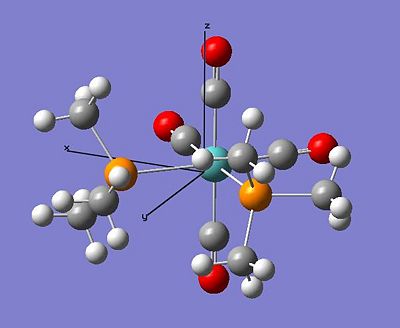
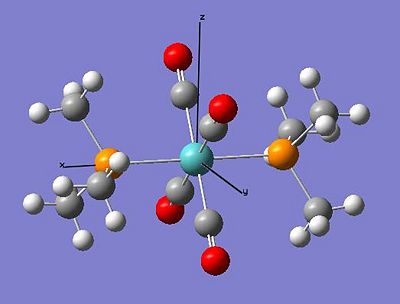
The Comparison of the Calculated Geometry with the Literature Geometry
The Beilstein database was searched using MDL Crossfire commander. No hits were returned for the drawn structure, or the IUPAC name. There were no hits for molecules containing bothnthe word 'molybdenum' and the word 'phosphine' anywhere in the chemical (including within other words).
The search parameter used for the last search. CN="*Molybdenum*" and CN="*phosphine*"
All the structures of molecules including the word 'molybdenum' or 'Mo' were quickly examined (there was a hitset of 134) yet there seemed no suitible octahedral complexes.
Scifinder Scholar could not be used because the were no available licences every time I tried to run the program.
Google Scholar returned no appropriate hits for "tetracarbonylbis(trimethylphosphine) Molybdenum" bis(trimethylphosphine) tetracarbonyl Molybdenum or tetracarbonylbistrimethylphosphine Molybdenum.
Web of Science also returned no useful results with these search terms, so it was decided to that my time would be used more efficiently comparing my molecule to the cis-tetracarbonylbis(dimethylphenyl) Molybdenum complex in the literature provided as references to this section:
"Steric contributions to the solid-state structures of bis(phosphine) derivatives of molybdenum carbonyl. X-ray structural studies of cis-Mo(CO)4[PPh3-nMen]2 (n = 0, 1, 2)", F. Albert Cotton, Donald J. Darensbourg, Simonetta Klein, and Brian W. S. Kolthammer, Inorg. Chem., 21, (1982), p294-299
The results were checked against this literature value to see if the calculation had produced a reasonable result.
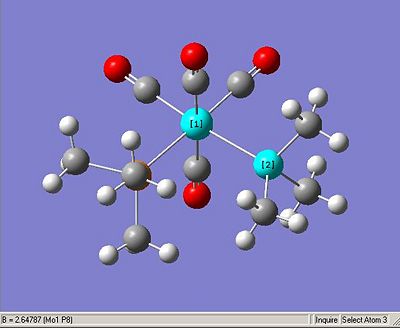
The literature complex showed an average P-Mo bond length of 2.529(4)Å compared to my computed cis-complex of 2.64687Å. This is close enough to confirm that the method employed in the computation has arrived at a reasonable result. My complex would indeed be expected to have a marginally shorter bond length as it has 3 methyl substituents instead of one phenyl and two methyl and is hence subject to less steric strain. This relaxation of steric strain would naturally cause a shorter Mo-P bond length. My trans complex has a bond length of 2.57176Å, fairly significantly shorter but, again within the region expected upon considering that the trans complex is under significantly less steric strain than either the computed cis or the literature trans complex. This is because in the trans complex the large phosphine ligands are not thrust together into such close proximity.
Likewise the P-Mo-P bond angle in the computed cis complex is 95.316° whereas the literature complex shows the equivalent angle to be 94.78°. This shows decent enough agreement but is still unexpected in that the molecule with the smaller subsituents is calculated to be more distorted from the octahedral geometry (90°) than the literature complex which has the larger dimethylphenylphosphine substituent. The computed complex has a P-Mo-P bond angle of 180° and I would have been very surprised if it ahd not, as the vector sum of all van der waal repulsion would be in the direction of the Mo-P bond and hence there would be no reason for it to distort this particular angle away from what would be expected from a perfectly octahedral geometry.
The average C-O bond length in the literature complex is 1.14Å and this compares to 1.188Å in the cis and 1.190Å in my trans complex.Both of these values values are very similar suggesting the the computational model predicts a very appropriate level of π-back bond in to the carbonyls in both complexes.
The C-Mo bond length in the literature complex for the carbonyls that are trans to a phosphine group is 1.982Å whereas the carbonyls that are trans to another CO ligand have a bond length of 2.016Å. This compares to my cis complex which has bond lengths of 1.9299Å and 2.03248Å respectively. This shows a very good agreement and even shows the same relationship in terms of the two carbonyl positions. The trans complex has only one carbonyl environment and all the Mo-C bond lengths are 2.02859Å.
In conclusion the computational model seems to have given a reasonable geometry complex optimisation compared with literature values, but may have systematically caused the bond lengths to be slightly too long.
Investigating IR Vibrational Frequencies of a Complex
These optimised geometry was then subjection to a frequency calculation (using the same method and basis set) and the IR frequencies were calculated.
In addition by searching last years lab scripts as advised the following reference for the cis- IR vibrations in a similar complex was found:
A. D. Allen and P. F. Barrett, Can. J. Chem., 1968, 46, 1649.
99 distinct vibrations were computed for both the cis and the trans complexes (3N-6). The most significant ones to characterise the complex shall be the C-O vibrations that cause a change in dipole moment because these are visible on an IR spectrum, very well defined and depend highly on the co ligands and co-ligand position.
The cis complex has 4 active C-O stretches (as is consistent with a C2v symmetry) at 1960.44Hz, 1869.95Hz and 1850.71Hz 1848Hz compared to lit 2005Hz, 1890Hz, 1875Hz and 1818Hz. The reason for the higher frequencies compared to the literature compound is that the phosphine in the literature compaound is triphenyl phosphine and that inducts electrons into the phosphine making it sigma donate more strongly into the Molybedum. This makes the Molybdeum more electron rich and hence will participate in a higher degree of backbonding with the carbonyls causing their C-O pi bonding to be weakened. This will lower the IR stretching frequencies of of vibrations associated with these bonds.
The computed trans complex has only 2 IR active CO stretches at 1838.95Hz and 1839.2Hz. The other C-O stretching frequencies at 1954.38 and 1882.63 are synchronous and due to the higher symmetry of the molecule, each C-O vibration causes a change in dipole moment that exactly cancels out the change in dipole moment caused by the CO trans to it. As every CO has a CO partner in the trans position in it only the two asynchronous vibrations that give a change in dipole moment.
The Energies of the Geometries
The cis geometry was found to have an energy of -2030457.29 KJmol-1 and the trans was found to have an energy of -2030449.69 KJmol-1. The means that the cis conformer is actually lower in energy by 7.60 KJmol-1 which is surprising considering that there would be expected to be significantly more steric strain in that geometry. To alter the relative ordering of the geometry, I would change the phosphine substituent for more sterically bulky fragments, isobutane for example. This will cause more steric repulsions and make the trans ligand lower in energy.
Day 3: The investigation of Ammonia
Ammonia was drawn and optimised in Gaussview using a DFT B3LYP method with a 6-31G basis set.
Symmetry
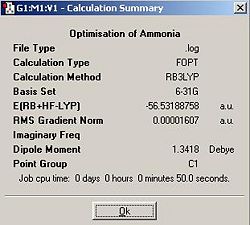
In this section I used a 6-31G basis set and the B3LYP method for all optimisations. Ammonia was drawn and optimised. The summary of the output is shown below
The ammonia was redrawn with one of was set to 1.01A, and the program was reoptimised.
A second possible geometry of ammonia in which the molecule is trigonal planer (the geometry of the transition state during an inversion) was optimised. the result is shown below.
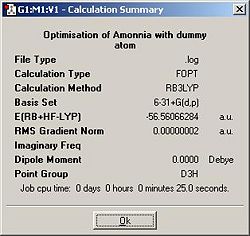
Discussion
When the input molecule was of higher symmetry for example D3h rather than C1 the geometry of the output was constrained to also be high symmetry because symmetry breaking transformations are not permitted in by the program. The lower the symmetry, the longer the calculation took because knowing that the symmetry of the optimised molecule will be high severely limits the possible geomtries that can be permitted. Essentially, if a molecule has a mirror plane, it makes the calculations significantly easier because only half the molecule need to be optimised (with any interactions at the edge being being returned in an identical fashion)and then mirrored to generate the other half. Consequently, as the optimisation will never involving breaking the symmetry, the higher the symmetry of the input molecule, the more constrained and hence quicker the calculations required to optimised it will be.
The lowest energy geometry is the one in which a single bond is altered to be 1.01Å.This came as a surprise to me as I would have thought this restriction on the allowed geomtries would have pushed the energy higher (surely any manually altered geometry would be higher in energy than one in which the program has a free reign to optimise.) On further contemplation I decided that by inputing a file with low symmetry, the system is actually less constrained in its optimisation; it no longer is forced to retain any symmetry. It still goes against common sense, which suggests that a molecule of ammonia's lowest energy geometry would indeed be C3V, but can be rationalised by realisation that the calculation is now allowed to consider any geometry to lower the energy, not merely the C3V geometries, and hence it is not entirely reasonable for it to give a marginally lower energy than the geometry with the C3V input.
1 au = 2625.5 kJmol-1
Source: http://www.rsc.org/ej/P2/2002/b201887j.pdf
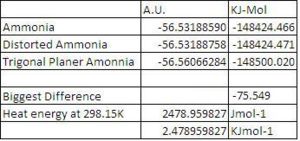
I believe that the difference in energy between the highest and lowest configurations, -75.549 KJMol-1 is significant, because it is an order of magnitude larger than the heat energy per mole present at room temperature, which was calculated by multiplying the temperature by the gas constant, R. This means that there will only a small percentage of molecules present in ammonia gas at room temperature that will have enough energy to ring flip.
Methods
Like the previous exercise, unadulterated C3V ammonia, as well trigonal planer D3h ammonia were optimised. This time a 6-311G+(d,p) basis set and the MP2 method were used.
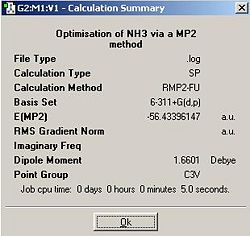
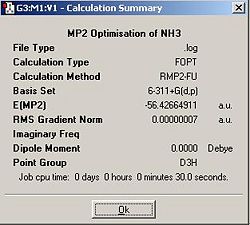
The optimisation initially assigned a C3 symmetry due to rounding errors inherent in the method. The input file was altered to remove these and the calculation was resubmitted. The lower calculation time for the C3v method may be a result of the fact that I explicitally constrained my input and optimised geometry to a C3v symmetry, to overcome the previous problem in which rounding errors caused the program to assign a lower symmetry.
The activation energy of the inversion will be the difference in energy between the initial geometry and the D3h trigonal planer intermediate.
EA = -56.42664911 a.u. - - 56.43396147 a.u.
EA = 0.00731236 a.u. = 19.198601 KJmol-1
As would be expected, the more weighty MP2 method resulted in a marginally lower energy for both conformations and this lowering was more pronounced on the D3h transition state.Consequently the activation energy for the ring flip is a third of the predicted EA by the previous B3LYP method. This EA agrees much more strongly with the literature value, 24.3 kJ/mol-1. The calculated value of the EA may be too low because of the approximations inherent in any quantum mechanical calculation. A more rigorous method may be used to give a better result but the calculation will take far longer.
Investigation into the vibrational frequencies
The Vibrational frequencies for the C3v and the D3h structure were calculated using a B3LYP/6-31G method.
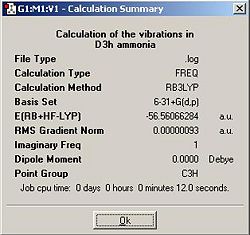
The results of these two calculations are shown below.
| Vibration on C3v NH3 | Vibration on D3h NH3 |
|---|---|
 Name: Vibration 2. Description: The central N atom vibrates up and down along the Z axis while the other 3 hydrogen remain stationary Frequency: 1576.58Hz |
 Name: Vibration 1. Description: The central N atom vibrates up and down along the Z axis while the other 3 hydrogen remain stationary Frequency: -768.258Hz |
 Name: Vibration 2. Description: 2 Hydrogens bend in the XY plane sychronously. All other atoms remain stationary. Frequency: 1680.47Hz |
Name: Vibration 1. Description: 2 Hydrogens bend in the XY plane sychronously. All other atoms remain stationary. Frequency: -768.258Hz |
 Name: Vibration 3. Description: 1 hydrogen bends in the XY plane. the rest of the molecule rotates in the opposite direction so that angular momentum in conserved. Frequency: 1680.47Hz |
Name: Vibration 3. Description: 1 hydrogen bends in the XY plane. the rest of the molecule rotates in the opposite direction so that angular momentum in conserved. Frequency: 1578.58Hz |
 Name: Vibration 4. Description: All the hydrogens undergo stretches along their bonds. Frequency: 3575.43Hz |
Name: Vibration 4. Description: All the hydrogens undergo stretches along their bonds. Frequency: 3625.18Hz |
 Name: Vibration 6. Description: Two hydrogens participate in stretches along their bonds, but asynchronously. Frequency: 3775.76Hz |
Name: Vibration 5. Description: Two hydrogens participate in stretches along their bonds, but asynchronously. Frequency: 3843.66Hz |
 Name: Vibration 5. Description: Two hydrogens participate in stretches along their bonds, asynchronously with the third that also performs a stretch along its bond. Frequency: 3775.76Hz |
Name: Vibration 6. Description:Two hydrogens participate in stretches along their bonds, asynchronously with the third that also performs a stretch along its bond. Frequency: 3843.66Hz |
Note the name of the vibration. Vibration 6 in D3h NH3 corresponds to vibration 5 in C3V and vis versa.
Discussion
There are 5 positive frequencies in the D3h symmetry NH3 and 5 in the C3v symmetry NH3. The transition state geometry ammonia has it's single negative frequency vibration at -768.258Hz. The vibration that follows the path of inversion is vibration one in which the central atom vibrates up and down the z axis.
The Mini Project: Fuels of the Future
Much work has been done to try and capture gaseous Hydrogen as a component in a solid molecule or complex so that it can be transported and released without the need to pressurise the gas. Pressurising the gas is undesirable for two reasons. Firstly, significant energy is required to perform the pressurisation, and secondly, vehicles moving at high speed carrying pressurised flammable gasses are at prone to explosion upon collision.
Storing the hydrogen as the solid, NH3BH3, is a promising concept for a number of reasons. Firstly each mole of the solid could potentially release 3 moles of H2, a large proportion of the product to reactant. In reality only 2 moles are released because the product produced, borazine, also contains hydrogen. Secondly it is a stable solid a room temperature and hence ideal to use as a fuel. To make the product, ammonium borohydride (NH4BH4)is produced in situ from NH4X and MBH4 salts (X = Cl, F, M = Na, Li) in liquid NH3,. Most of the ammonia is removed and tetrahydrofuran (THF) is added which causes the ammonium borohydrate to decompose to ammonia borane.
The two major drawbacks to using ammonia borane. The first is that the biproduct produced after the hydrogen is released, borazine, B3N3H6, a 6 membered ring of alternating B and N atoms, each with a single hydrogen attached, inhibits proton exchange membrane fuel cells. The second significant drawback is that the reaction involved in forming the fuel is not reversible; it is synthetically very inconvenient to turn borazine back into ammonia borane. Clearly the ideal fuel would be easily and efficiantly regenerated if in some way the system was given energy (much like H2 can be regenerated from H2O if electrically energy is applied via electrolysis.
Molecular Modelling Investigation Ammonia Borane
The molecule was drawn using gaussview and optimised using guassview. As all the elements involved are first row elements on the periodic table, no d-orbital interactions are anticipated. Consequently a B3LYP method and a 3-21G basis set were used for the DFT optimisation.
The initial optimisation produced a staggered molecule, but showed no formal bond between the boron and the nitrogen atoms, and the interatomic distance, 1.68512Å, was significantly longer than the literature value calculated from neutron diffraction 1.58(2)Å1.
The calculation was performed again except on this occasion, the input molecule was drawn in chembio3D and formal charges were added; the nitrogen was cationic and the boron was anionic.
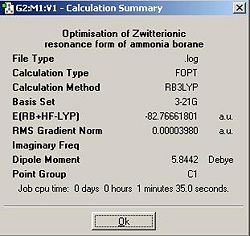
The optimised molecule was shown to have an almost identical N-B interatomic distance as is evident from the diagram and also shows the incorrect symmetry, C1. A perfectly staggered molecule would be expected to have C3v point group. This potential misassignment of the point group could potentially be a result of the input file having small rounding errors (as discussed in previous exercises). To see if this made any difference the molecule input file was changed and all the dihedral angles were made a multiple of 60, all B-H angles were made equal, all N-H angles were made equal and the bond angles for the SP3 hybridised centres were made π/2+sin-1(1/3), in approximate numerical terms (calculated by microsoft excel in conjunction with 'solver'), 109.471220636267°.
This high symmetry input was then optimised as before, and the output below was produced.
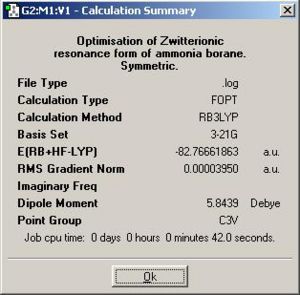
The raising of the symmetry did not impact significantly on the N-B bond length but did produce a high symmetry output file which is a better approximation to the staggered conformation of the molecule. In reality, however, the vibrations in the molecule caused by thermal agitation will break the symmetry of the molecule if ever observed but the average of the all the vibrations would be the higher symmetry staggered conformation.
Lowest energy structure Discussion
Though the N-B interatomic distance is rather larger compared to the literature value, all the different variations on the optimisation have shown that the stagger conformation is lowest energy. This is as would be expected considering 1-4 van der waals repulsions between the hydrogens.This is analogous to the isoelectronic and isostructual ethane which favours the staggered position for this reason.
Further Comparison with Ethane
The eclipsed form of ammonia borane will be drawn and optimised(insuring the input symmetry is C3v)and the difference between the staggered and eclipsed conformations and compare this with the equivilent conformations in ethane. I predict that the difference in energy between the two conformations will be lower in ammonia borane due to the much larger length of the B-N bond compared to the C-C bond. This will reduce the steric repulsions experienced by the 1-4 hydrogens and hence lower the energy of the eclipsed conformation.The C-C bond is predictied to be significantly shorter because there is a much better orbital overlap between a C atomic orbital and another C atomic orbital than between a a boron and a nitrogen atomic orbital. This is because there is a sizable electronegativity difference between the two elements and hence the energy of the atomic orbitals will be missmatched as well be the degree of diffusity.
Firstly the eclipsed conformation of ammonia borane was optimised.The input file dihedral bond angles for the optimised staggered conformation were altered so that the hydrogen atoms eclipsed each other. The optimisation was then carried out.
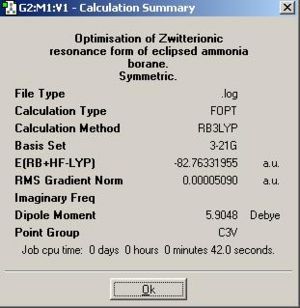
The energy was higher as predicted and the B-N internuclear distance was even longer (unsurprisingly as the increased 1-4 steric repulsions would be lessened by a longer B-N bond length and hence the molecule distorts to lower the energy).
Ethane was drawn in guassview and the same method was used as was used with ammonia borane to optimise its staggered conformation
The input file was modified as explained previously to convert the molecule into the eclipsed conformation.
Table of Energies and Bond Lengths
| Ammonia Borane Staggered | Ammonia Borane Eclipsed | Ethane Staggered | Ethane Eclipsed | |
|---|---|---|---|---|
| Bond Length (Å) | 1.68499 | 1.71129 | 1.54432 | 1.55996 |
| Energy (A.U.) | -82.76661863 | -82.76331955 | -79.40063889 | -79.39632464 |
| KJmol-1 | -217303.7572 | -217295.0955 | -208466.3774 | -208455.0503 |
| Difference in Energy Between Conformations (KJmol-1) | |
|---|---|
| Ammonia Borane | 8.66173454 |
| Ethane | 11.32706337 |
As predicted the the difference in energy between the staggered and the eclipsed molecules is greater in ethane than in ammonia borane. This will slightly increase the amount of free rotation in ammonia borane compared to ethane at the same temperature. As the amount of heat energy at room temperature per mole is 2.477KJmol-1 this is around the same order of magnitude and hence there will be a significant minority of molecules with enough energy to interconvert. According to the Boltzmann distribution there will be 3.037% of the ammonia borane molecules and 1.036% of the ethane with enough energy at any one time at 298.15K.
The Bonding present in the Compound
The bonding in ammonia borane is clearly different to its organic analogue ethane. There are clearly weaker interactions between the nitrogen and the Boron atoms and this is manifested in a longer bond length. This weaker bonding can be predicted from MO theory as it dictates that the strength on the interaction is highly dependant on the relative energies of the interacting orbitals, the relative sizes, the absolute sizes (and dispersion) and the geometric overlap.
The Relative Energies of the Interacting Orbitals
In ethane the two interacting molecular orbitals from the two CH3 units are identical. In ammonia borane they will be very different due to the difference in electronegativity. Ammonia is more electronegative so would be expected to have atomic orbitals much lower in energy. The orbitals that are expected to interact are the HOMO SP3 hybridised lone pair on the nitrogen and the LUMO vacant unhybridised p-orbital on the borane, and the nitrogen HOMO is expected to be lower in energy. This energy cap will lower the strength of the interaction.
The Sizes of Interacting Orbitals
As in the previous case ethane's two CH3 fragments interact very strongly as they are the same size orbitals. Also both carbons are first row elements so will interact strongly (their absolute orbital size are small and not defuse.
Both Boron and Ammonia are from the same row on the periodic table so it is expected for the HOMO on the ammonia and the LUMO on the borane to be approximately the same size. However the increased electronegativity on the the NH3 will cause the molecular orbital to be less dispersed. Both atoms are first row elements so will form stronger bonds than, say, two 3rd row elements.
The Geometric Overlap
Both the CH3 fragments and the BH3 and NH3 fragments have the same substitutions, Hydrogen and hence will be subjected to very similar constraints on how close they can approach each other to interact. Consequently both are fairly equivalent in terms of allowed geometric overlap.
The Computed Molecular Orbitals
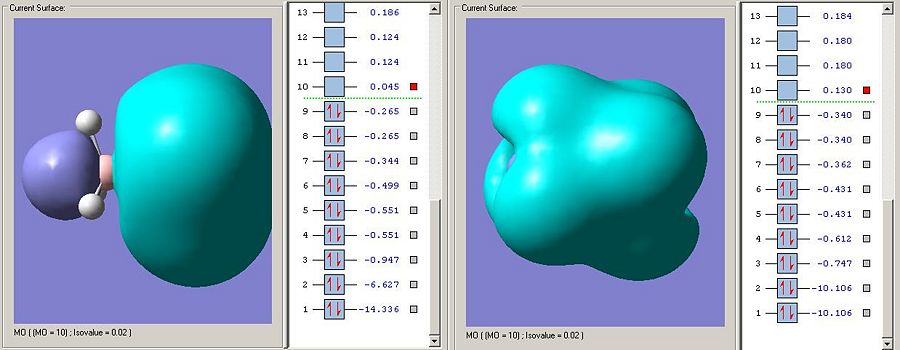
The molecular orbitals for ammonia borane and ethane were calculated
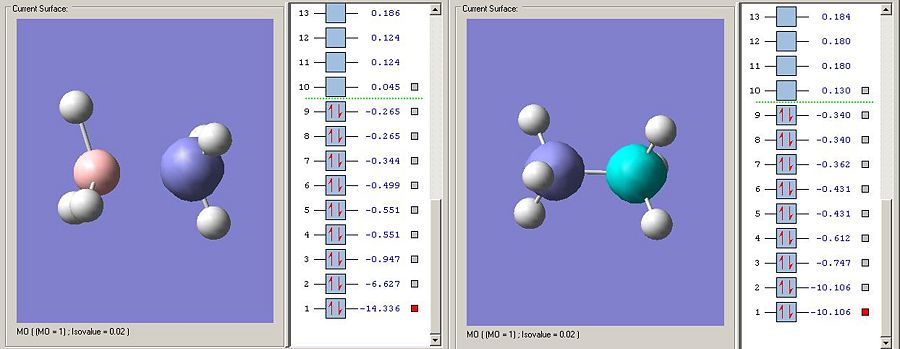
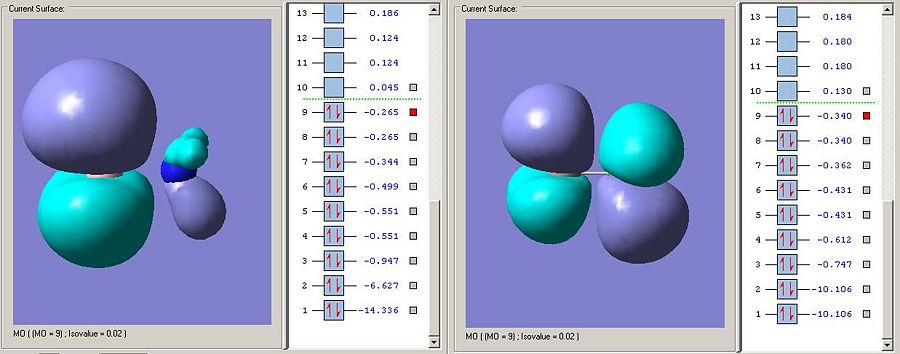
As predicted the energy for the equivilent 1S atomic orbitals on ammonia are much lower in energy than carbon. In this instance the nitrogen 1S orbital is non bonding as it is so low in energy.
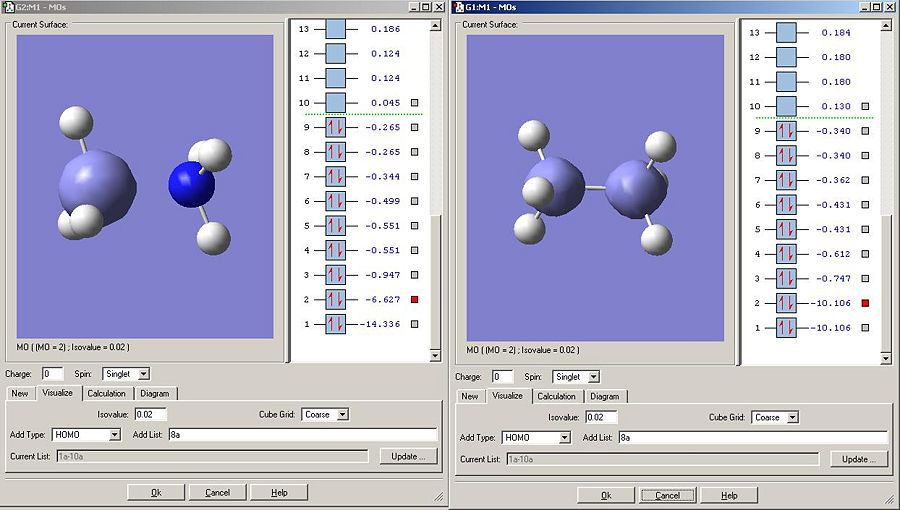
As predicted, borane, being less electronegative than carbon has higher energy 1S orbitals.
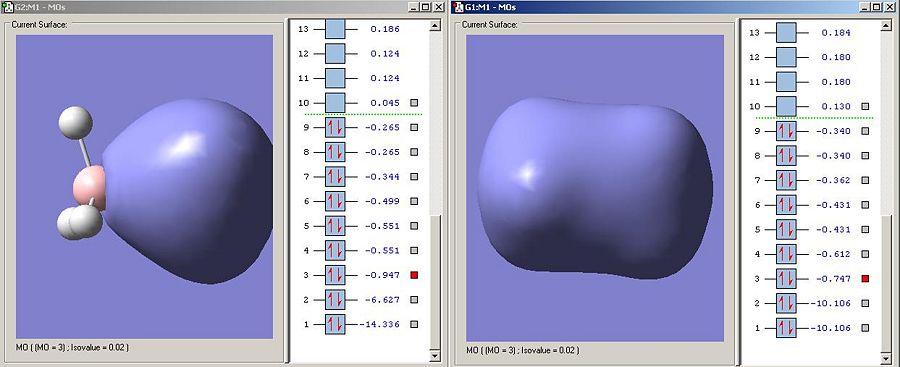
Bonding orbitals between to differing electronegativity tend to exhibit more charactor from the more electronegative fragments atomic orbitals. This is exhibited here as the electrodensity is very much centred around the nitrogen, the more electronegative element. This distortion is not present in ethane. Interestingly the B-N orbital is lower in energy than the C-C bond,and this suggests that this particular sigma-bonding orbital is stronger in ammonia borane, though this is contrary to the criteria for the strength of interaction already discussed.
Further evidence that the MO3 sigma-bonding type interaction is stronger in B-N than in C-C is that its corresponding sigma-antibonding orbital is much higher in energy. Whereas MO4 is the sigma antibonding type orbital described, the equivilent orbital in ammonia borane is in fact so high in energy its MO6.
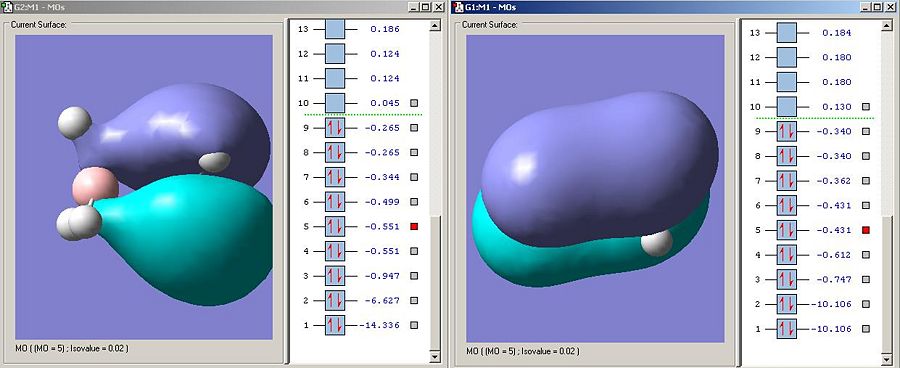
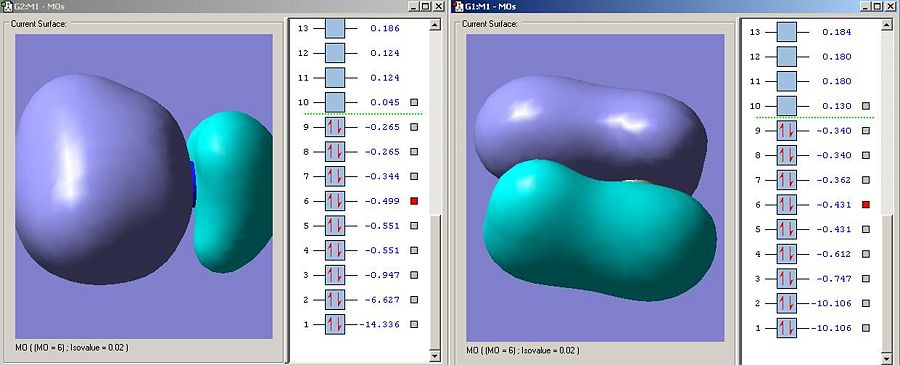
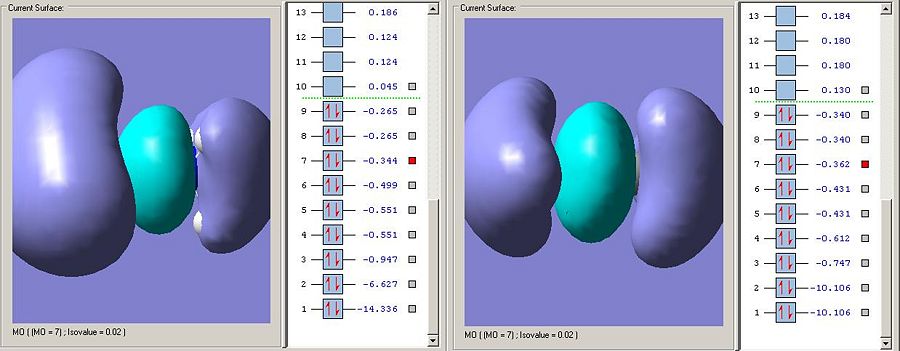
This is the important sigma-bonding type interaction because it is the one which most correstponds to the sigma bond observed in the molecules. The ammonia borane orbital is higher in energy suggesting it affords less stabalisation to the product than the sigma bond affort its methyl fragments. This suggests that the bonding will be weaker in ammonia borane than ethane as has been predicted.
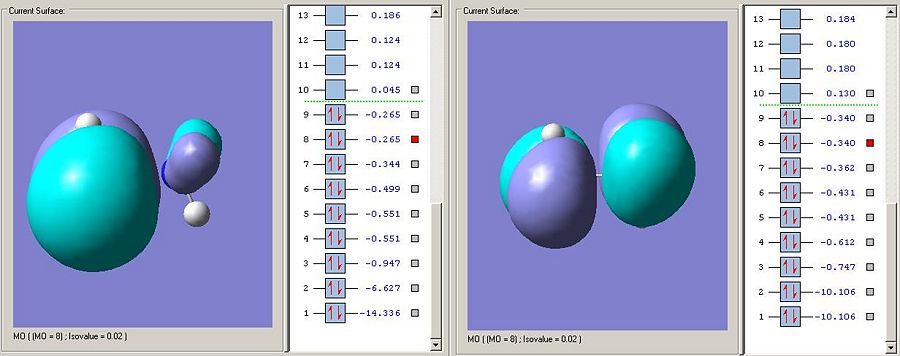
The LUMO on the ammonnia borane is the sigma antibodning orbital as is the LUMO on carbon. The fact that the LUMO is much lower in energy on the ammonia borane means that the bond is more susceptable to nucleophillic attack (espcially on borane looking at the elctron desity on the MO visualisation). This makes a lot of sense as the bond has been anticipated to be weaker and ammonia will be a far better leaving group than the CH3 fragment anion (the ammonia leaving group will be uncharged if the zwitterionic resonance form is attacked).
The Stability of the Products relative to the Reacts in the synthesis of Ammonia Borane
A B3LYP method and a 3-21G basis set were used for the DFT optimisation of the reactants and the products to get some idea of the standard enthalpies of the reaction.
NH4Cl
NaBH4
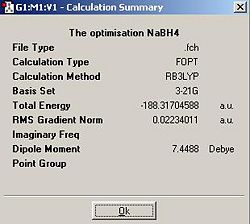
NH4BH4
NaCl
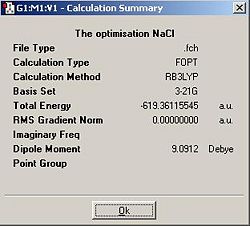
This type of optimisation may be inappropriate for modelling the energy of NaCl in this particular reaction because the molecule exists in an infinite ionic lattice while in the solid state and solid state structure is not modelled by this program.
H2
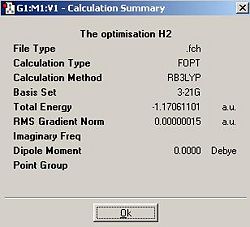
Discussion of the relative stabilities of the Products and Reactants
| a.u. | Kjmol-1 | |
|---|---|---|
| NH4Cl | -514.8506156 | -1351740.291 |
| NaBH4 | -188.3170459 | -494426.404 |
| Total energy for the reactants | -703.1676615 | -1846166.695 |
| NH4BH4 | -83.89065631 | -220254.9181 |
| NaCl | -619.3611555 | -1626132.714 |
| Total Energy for the intermediates | -703.2518118 | -1846387.632 |
| NH3BH3 | -82.76661863 | -217303.7572 |
| NaCl | -619.3611555 | -1626132.714 |
| H2 | -1.17061101 | -3073.439207 |
| Total energy for the products | -703.2983851 | -1846509.91 |
| Difference in energy between reactants and intermediates | -220.9366389 KJ-1 |
| Diference in energy between intermediates and products | -122.2782779 KJ-1 |
| Difference in energy between reactants and products | -343.2149168KJ -1 |
Clearly there is a very strong enthalpic driving force behind the formation of the formation of ammonia borane from the reactants. This is many due to the high stability of sodium chloride (ionic salts tend to be highly stable and hence low in energy). This has benifits but also drawbacks to the suitibility of ammonia borane as a solid container for hydrogen.
It is advantageous because the high thermodynamic driving force dorces the reaction to completion at very high yield.This is useful as it means there is no further purification step in making the fuel.
The major disadvantage is that the large change in energy inherent in the reaction means that the end product borazene cannot simply be 'recharged' with hydrogen my mixing it in the presence of an energy source. The reactants NaBH4 and NH4Cl are extremely high in energy require a series of reactions performed at extreme temperatures. Consequently in order to make ammonia borane a great deal of energy is required and the process involved in recharging the biproduct with more hydrogen is also lengthy and energetically unfavourable. This high energy requirement means that the process as it stands is highly unsuitable for use in the context of hydrogen fuel cells as the fundamental principle in using hydrogen is the energy efficiency of using hydrogen produced from the electrolysis of water to store energy produced from another source.
Solid State Structure of Ammonia Borane
Despite being isoelectronic ethane has a hugely lower melting point than ammonia borane. This explaination for this difference is of course to do with the differences in intermolecular bonding between the two groups.
A fairly facile explanation concerns the relative polarity of the two molecules. Ethane is entirely non-polar and hence the only intermolecular interactions open to it are instantaneous dipole induced-dipole interactions, van der waals interactions. These are caused by normal fluctuations of charge inducing another dipole in a nearby polarisable molecule and in doing so forming a temporary positive interaction. These tend to be weak and especially so in small molecules that are not particularly polarisable such as ethane. On the other hand NH3BH3 is polar with a dipole moment shown in previous optimisations to be 5.9048 debyes. This dipole will have a tenancy to cause other molecules to align with it and hence interact positively via a permanent dipole-dipole interaction. This is why, for example, H-Cl is a solid at room temperature whereas Cl2 is a gas.
A more involved explanation involves di-hydrogen bonding the molecular crystal lattice of ammonia borane.1 Neutron diffraction studies1 have shown the ammonia borane aligns itself in the crystal so that the Hydrogen atoms attached the Nitrogen atom can interact intermolecularly with a hydrogen atoms attached to boron atoms on other molecules. This interaction is similar to a H- interacting with a H+ because the hydrogen atom attached to the boron at will be marginally d-negative as the boron will have a slight electron donating effect and the hydrogen atom attached to the nitrogen will be slightly d-positive as the nitrogen will induct electrons away from it. This interaction is not trivial and has been predcted theoretically to be in the same region of strength, 16.7KJmol-1-25.1KJmol-1 2, as traditional hydrogen bonding. As the structure calculated by neutron diffraction found a very closepacked structure with a very high sumber of such dihydrogen intermolecular bonds it seems very likely that this is the cause of the differing properties.
If modelling the intermolecular interactions of the molecular via computational method is required,CRYSTAL can be used to calculate the molecular interactions in infinite lattices. In such an infinite latice a band structure will emerge and the difference in energy between the bonding interaction and the antibonding interaction will determine the strength of the bonding. I believe that an additional program not mentioned in module 3 will be required to optimise the geometry of the molecules within the crystal because the way in which CRYSTAL is used in module 3 seems to only predict the band structure, the density of states and the charge density, not in fact the geometry of the crystal (which is included in the input). One you have a system to generate an output energy for a given geometry input means that the variation theorem run as an iterative program can find a minimum energy geometry crystal coresponding to the crystal structure. This will be very expensive in terms of computational work however.
Aditional References
1. Klooster, W.T. (1999), "Study of the N-H...H-B Dihydrogen Bond Including the Crystal Structure of BH3NH3 by Neutron Diffraction", Journal of the American Chemical Society 121: pp. 6337–6343
2. Richardson, T. B.; deGala, S.; Crabtree, R. H.; Siegbahn, P. E. M. J. Am. Chem. Soc. 1995, 117, 12875