Rep:Mod:est

Module 3

Gareth Naylor

Cope Rearrangement

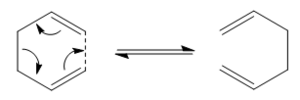
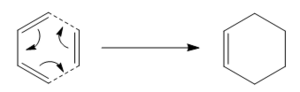
As well as modelling the structures and properties of molecules, programs such as Gaussview can also be used to study chemical reactivity. This can first be demonstrated using the Cope rearrangement of 1,5-hexadiene, specifically locating and analysing any low energy minima, also known as reactive intermediates, and high energy maxima, known commonly as transition states. The Cope rearrangement can be explained in simple terms as an alkyl group migrating in a (4n+2) electron process. A mechanism for the Cope rearrangement is shown in Figure 1.

Figure 1 - Mechanism for Cope Rearrangement

Wiest et al reported that DFT methods gave good results for the formation of transition states, however it was also noted that determining the nature of such transition states proved much more difficult. Such transition states could take either a chair or a boat form, with the chair structure having been found to lie at a lower energy.

Procedure

Using Gaussview a number of conformations of 1,5-hexadiene were separately produced, all of which contained an anti-linkage in the four central carbon atoms. These molecules were then cleaned using the Gaussview function and optimised using the HF (Hartree-Fock) functional and 3-21G basis set. The %mem was then set to 250MB. The .chk files from the results of these optimisations were loaded and a number of properties noted.

Results

These optimised structures can be analysed in terms of their energies and point groups. These results can be displayed in terms of whether they contain an anti- or gauche- central chain. The anti- structures are displayed in table 1, whilst the gauche structures are shown in table 2.

Table 1: anti- conformations of 1,5-hexadiene

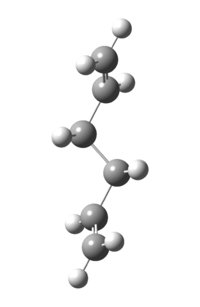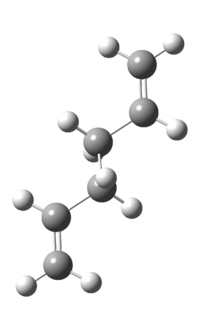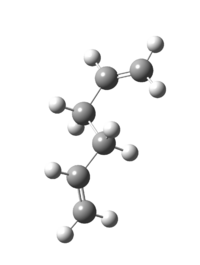Energy (a.u.)	-231.69260235	-231.69253506	-231.69097056
RMS gradient	0.00001929	0.00006411	0.00000614
Point group	C2	Ci	C1
Corresponding structure from Appendix 1	1	2	4

Table 2: gauche- conformations of 1,5-hexadiene

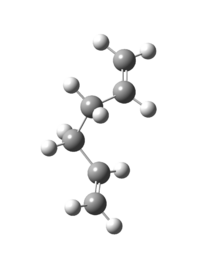Energy (a.u.)	-231.69153034	-231.68961576	-231.69266122
RMS gradient	0.00000795	0.00000373	0.00000735
Point group	C2	C1	C1
Corresponding structure from Appendix 1	4	5	3

From these results it can be seen that the lowest energy gauche conformation has a lower energy than the lowest energy anti conformation. This would not be the expected outcome from analysing the steric interactions of the molecules, however this can be rationalised from looking at the molecular orbitals. The HOMO's for both the gauche and the anti molecules are shown in figures 2 and 3.

Figure 2:anti HOMO

Figure 3:gauche HOMO

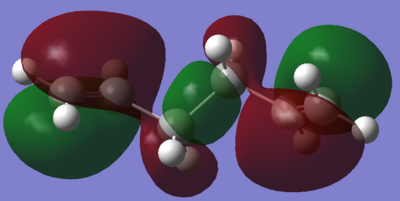
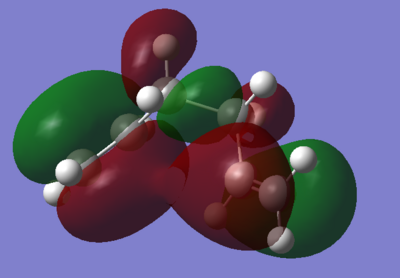
It is clear from figures 2 and 3 that the gauche conformer contains much more favourable interactions. This can be seen from the fact that some of the orbitals overlap, resulting in very good interactions. This is especially important for the interactions between the two alkene orbitals which stabilises the molecule greatly. On the other hand the most stable anti conformer has much smaller favourable interactions and the largest interactions are much further away from each other than for the gauche conformer.

The anti 2 conformer, shown in table 1 can be re-optimised using the DFT-B3LYP functional and 6-31G(d) basis set. This provides a more accurate simulation and should give a better optimised structure and lower energy. A comparison of the results for both methods is shown in table 3.

Table 3: Comparing properties of different computational methods for anti 2 structure

	HF 3-21G	DFT-B3LYP
Structure
Energy (a.u.)	-231.69253506	-234.61171330
C1-C2 Bond length (angstroms)	1.316	1.334
C2-C6 Bond length (angstroms)	1.509	1.504
C6-C9 Bond length (angstroms)	1.553	1.548
C1-C2-C6-C9 dihedral angle (degrees)	114.66	118.78
C2-C6-C9-C12 dihedral angle (degrees)	180.00	180.00

The major difference between these methods lies in the energies. The Density Functional Theory (DFT) model gives a considerably lower energy that the Hartree Fock (HF) method as it is a much more accurate method. The C-C bond lengths are extremely similar in the two structures, however the C2-C6-C9-C12 dihedral angle in each structure also changes a lot. It can be assumed that this change in the dihedral angle stabilises the structure.

Frequency

Procedure

A frequency calculation can then be carried out in order to confirm that an energy minimum has been obtained. This calculation was carried out using the B3LYP/6-31G* optimised structure. The calculation was simply done by selecting frequency under the job type tab. The job was then submitted and when it finished the log file was opened and the vibrational results analysed. The thermochemical properties of the molecule can also be computed, taken at 298.15K. These are shown in figure 4.

Figure 4 - Thermal properties for anti 2 structure optimised using DFT method

The energies given in these calculations can be defined as:taken from phys3 page
Sum of electronic and zero point Energies: the potential energy at 0 K including the zero-point vibrational energy (E = E_elec + ZPE)
Sum of electric and thermal energies: the energy at 298.15 K and 1 atm of pressure including contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + Evib + Erot + Etrans)
sum of electronic and thermal enthalpies: energy with an additional correction for RT (H = E + RT) which is particularly important when looking at dissociation reactions
sum of electronic and thermal free energies: energy including the entropic contribution to the free energy (G = H - TS)

Optimising the "Chair" and "Boat" transition structures

In order for a reaction such as the Cope rearrangement to occur a high energy transition state must form on the energy path between the reactant and the product molecules. This transition state can take either a "chair" or a "boat" structure. These two transition states can then be compared in terms of their properties and related back to the structures of 1,5 hexadiene produced in the previous exercise. This process started with a simple allyl fragment.

Chair

Procedure

An allyl fragment (CH₂CHCH₂) was copied into a molecule window and optimised using the HF/3-21G method. The optimised structure and properties are shown in figure 5. The HF/3-21G method was used for all calculations in this process as it gave the greatest accuracy:time ratio. Two versions of this optimised structure were then pasted into a new molecule window and orientated roughly into the shape of a chair transition state, demonstrated in Appendix 2. It is essential in this orientation that the terminal carbons are approximately 2.2 Angstroms away from each other. This is because it will be much more difficult to find the optimised transition state structure of the molecule if the guess structure of the molecule is not similar to the TS structure. The underlying theory behind this method involves the Hessian matrix, which allows the calculation to locate the negative direction of curvature.

Figure 5 - Optimised structure for allyl fragment

This chair representation of the transition state structure can now be optimised using two different methods. The first optimisation used the TS (Berny) job type, entered in the Gaussian Calculation menu. The force constants were set to be calculated once, whilst in the Keywords section, Opt=NoEigen was entered. This job was submitted for calculation and when it was finished the log file was opened and checked to see if the job had converged properly.

The next method of optimisation involved freezing the reaction coordinate in order to obtain a minimum for the rest of the structure. It is then possible to unfreeze the rest of the reaction coordinate and perform another TS (Berny) optimisation to find the most accurate optimised structure. It would be predicted that this technique would give the lowest energy structure as the "guess structure" would be more accurate in this case due to the initial coordinate freeze.

The frozen coordinate method is started using the same initial "guess structure" of two allyl groups as the TS (berny) method. The Redundant Coord Editor was then used to set the bond distance between each of the two sets of terminal carbons to 2.2 Angstroms. This was done by selecting the Bond and Freeze Coordinate options. The structure was then optimised to a minimum, the line Opt=ModRedundant should be present in the input line.

The resulting optimised structure, which retained C-C bond lengths of 2.2 Angstroms, was opened in the form of a chk file. It was then necessary to unfreeze the structure, as detailed above, in order to locate the transition state of the structure. This process was again carried out using the Redundant Coord editor, this time selecting the bond and derivative options. This process should again be repeated for both sets of terminal C-C bonds. A TS (berny) optimisation was then carried out, ensuring that force constants were not calculated The results of these there different optimisation techniques are shown in the next section.

Results

Each of the three optimisations gave very similar structures, therefore it was necessary to analyse the properties of the structures in order to distinguish between the optimisations. The vibrations section in the results for the TS (Berny) method was checked for negative frequencies, which signify the formation of the transition state. The structure and properties of this transition state, as well as an animation of the negative frequency are shown in table 4.

Table 4: Structures, animations and properties for both TS (Berny) and Frozen coordinate optimisation methods.

	TS (berny)	Frozen	Frozen followed by TS (berny)
Structure
Energy (a. u.)	-231.619	-231.615	-231.619
Terminal C-C distance (Angstroms)	2.021	2.000	2.0273
Imaginary Frequency Value	-818	-765	-818
Animation of Imaginary Frequency

All of the imaginary frequency animations shown in table 4 above correspond to motions representing the Cope rearrangement. All three show asymmetric stretches which represent bond breaking and bond forming motions between the terminal carbons. The energies of the structures given by the two transition state formation methods (TS (berny) and frozen followed by TS (berny) can be compared in order to determine which is the optimum route to a transition state structure. From the data shown in table 4 it can be seen that there is no difference in energies between the methods whilst there is also only a very small difference in the bond angles and no difference in the imaginery frequencies. Therefore it can be concluded from this data that the method of finding the transition state is not particularly important.

Boat

Procedure

In order to optimise the boat structure the QST2 method will be used. A QST2 calculation takes the structures of both a reactant and a product and follows the reaction path between the structures, in order to find a high energy transition state.

It is essential in this calculation that the reactant and product structures correspond to each other in terms of their atom numbering. In order to make the reactant and product correspond, firstly two copies of the same optimised anti 2 structure were copied into the same window but into different MolGroups. The molecules were numbered as in figures 6 and 7, which corresponded to the reactant and the product of the Cope rearrangement.

Figure 6 - Labelling of reactant molecule

Figure 7 - Labelling of product molecule

An attempt at a QST2 calculation was then made using these structures. This was done using a simple Gaussian calculation with a job type of Opt+Freq, optimising to a QST2 transition state. The result of this calculation and the reason for its failure are explained in the results section below.

In order to ensure a working QST2 calculation, the structures of the reactant and product molecules must resemble the desired transition state more so than they did in figures 5 and 6. Therefore it was necessary to modify certain angles within the molecules in order to make the structures more similar to the boat transition structure. Taking the reactant molecule as an example, the C-C-C-C dihedral angle should be changed to 0^o whilst both the C-C-C and the C-C-C bond angles should be modified to 100^o. This gave the structures shown in figures 8 and 9.

Figure 8 - Labelling of reactant molecule

Figure 9 - Labelling of product molecule

The QST2 calculation can be run using the same conditions as specified in the earlier failed calculation. The results of this calculation is shown in the results sections below.

Results

Firstly the structure of the initial QST2 calculation, which failed, can be discussed. This is shown in figure 10.

Figure 10 - Structure of failed QST2

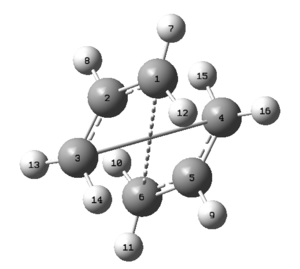
The structure of the failed QST2 represents the chair transition state. This can be explained by using Hammonds postulate which states that the transition state should resemble either the reactant or the products. Hence, since the calculation uses the same reactants and products as the chair transition state investigation it would be expected that a chair transition structure should be formed.

From analysing certain structural properties of the actual chair transition state and the failed QST2 chair TS, certain properties can be compared. The major difference in the structures lies in the bond distances between the terminal carbons. In the QST2 chair structure the two allyl groups are much further apart (3.52Angstroms) compared to the proper chair TS (2.02Angstroms) however, this can be attributed to the fact that in the QST2 calculation bond lengths were not set as they were in the TS (berny) case.

When the bond and dihedral angles between the carbons were altered this gave a much more accurate boat transition state. The structure for this can be viewed in figure 11.

Figure 11 - Structure of successful QST2

The successful QST2 method yielded some interesting properties. Firstly the energy of the structure was found to be -231.602a.u. As expected the boat structure has a higher energy than the chair structure. The imaginary frequency of this structure was found to be -839.33cm^-1. The corresponding animation is shown in figure 9. The terminal C-C bond distance in this structure is 2.14Angstroms, which is greater than that of the chair structure. This is a major reason for the boat structure being higher in energy.

IRC calculations

Now that transition states have been found for both the chair and boat structures it is possible to follow the reaction coordinate in either direction to lead to either the the reactants, products or a reactive intermediate. In the same way as the transition state investigation will find a high energy state, an Intrinsic Reaction Coordinate (IRC) method will search for a low energy intermediate. Both the chair and the boat structures can be investigated in order to find the conformer of 1,5-hexadiene that they have been formed from and go on to produce. The theory behind the IRC involves progressing down the energy curve where the gradient is steepest in a number of small geometry steps until a low energy intermediate is reached.

Procedure

Using the chk file from the chair and boat transition structures a gaussian calculation was carried out using IRC as the job type. This was done separately for each transition state. The calculation should proceed in the forward direction only. It is only necessary to model one one direction because the reaction is symmetrical. Ensure that the force constants are only calculated once and set the number of points along the IRC to be 50. These calculations were then run and the results shown in below.

Results

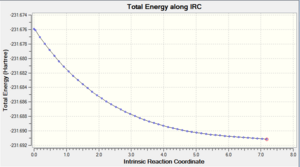
The results for the IRC calculations did not show minima. This was evident from viewing the IRC path graphs. It was therefore necessary to optimise to a minimum the final structures produced from the IRC, in order to produce one of the 1,5-hexadiene structures optimised earlier. The results of these optimisations are shown in table 5.

Table 5: Structures, animations and properties for both TS (Berny) and Frozen coordinate optimisation methods.

	Chair	Boat
Pre-minimization Structure
IRC path
RMS gradient of IRC path
Pre-minimization energy (a. u.)	-231.69113	-231.67898
Post minimisation structure
Post minimisation energy (a.u.)	-231.69166	-231.69266
Corresponding conformer of 1,5-hexadiene	gauche 2	gauche 3

It can be seen from these IRC gradient curves that a minimum was not found on the initial IRC. This is obvious because the gradients of these graphs do not converge to zero. Therefore it was necessary to perform the minimisations in order to gain the structures of the reactant/product in this reaction. It was interesting to note that the higher energy boat transition state was derived from the lowest energy gauche conformation and the chair transition state was formed from a higher energy gauche conformation. This shows that the structure of the reactant has no bearing on the transition state formed.

Calculating Activation Energies

Using the transition states computed it was also possible to predict a range of energy values, including the activation energies. The procedure for finding these energies involved optimising the HF/3-21G transition states to the B3LYP/6-31G level of theory. The structures and energies produced by the two levels of theory can be compared in table 6 and 7.

Table 6: Comparison of HF and DFT methods of optimisation for chair structure

	HF/3-21G	DFT/6-31G(d)
Structure
Energy (a.u.)	-231.61932	-234.55698
Terminal C-C bond lengths (angstroms)	2.02029	1.96776

Table 7: Comparison of HF and DFT methods of optimisation for boat structure

	HF/3-21G	DFT/6-31G(d)
Structure
Energy (a.u.)	-231.60280	-234.54309
Terminal C-C bond lengths (angstroms)	2.14016	2.20702

These comparisons show that, in terms of the energies of the molecules, the DFT method is much more accurate as it gives a much lower energy conformation in both cases. On the other hand, the bond lengths do not show any trends between the two methods.

The activation energies of the chair and the boat reactions can be calculated by taking the energy of the reactant structure from the energy of the transition state structure. These energies are shown in table 7.

Table 7: Comparison of activation energies for chair and boat transition structures

	chair	boat
Reactant Energy (a.u.)	-231.69166	-231.69266
Transition State energy (a.u.)	-231.619	-231.602
Activation Energy (a.u.)	0.07266	0.09066

This data shows that the boat structure has a greater activation energy than the chair structure. This means that if the kinetic reaction was followed then the chair transition state would be produced as it has the lower energy transition state.

The Diels Alder Cycloaddition

The Diels alder reaction is effectively an intermolecular version of the Cope rearrangement calculated earlier. Both reactions are pericyclic, however the Diels Alder is also a cyclo addition reaction involving 4n+2 electrons. This means it is an allowed reaction. Diels Alder reactions involve both a dienophile and a diene, in this case, ethylene being the diene and butadiene taking the role of the dienophile. The interactions between the molecular orbitals are particularly important in this reaction as the reaction will only take place when the orbitals have the same symmetry properties. A mechanistic representation of the Diels Alder reaction is shown in figure 12.

Figure 12 - Mechanism for Diels Alder Reaction

Many cycloaddition reactions, like the one being studied here can be stereoselective. This will be investigated more in the reaction of cyclohexa-1,3-diene with maleic anhydride shown below. The stereoselectivity of the reaction will depend on the stability of the transition state. In general the endo transition state predominates in most reactions as the endo transition state is lower in energy than the exo transition state.

Firstly the molecular orbitals of butadiene and ethylene were computed in order to prove that the reaction is allowed. This was done using the am1 semi-empirical computational method. The basic structures of the optimised molecules are shown in table 8.

Table 8: HOMO and LUMO orbitals of butadiene and ethene

	Butadiene	ethylene
HOMO
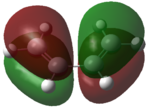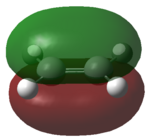LUMO

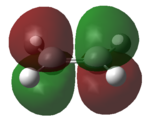From these molecular orbitals it is clear to see that either pair of HOMO-LUMO interactions would be allowed. This is due to the orbitals both having the same symmetry properties. For example the interaction of the LUMO of the ethylene and the HOMO of the diene would be allowed as both orbitals are antisymmetric. In practice it could be predicted that the HOMO of the diene would be more likely to interact with the LUMO of ethylene due to the greater electron density present on the diene.

Finding a transition state for a Diels Alder reaction

It was next possible to attempt to find a transition state for the Diels Alder reaction. This was initially carried out using am1 optimised molecules, in an envelope type geometry. This envelope geometry constituted of the ethylene molecule slightly above the plane of the diene molecule. The frozen coordinate technique, with terminal C-C bond lengths of 2.0 Angstroms, was first employed in an optimisation in order to ensure that the geometries of the molecule remained constant. The coordinates were then unfrozen and an opt+freq calculation run, in order to find a transition state using the TS (Berny) method. This also used the am1 method. This gave a transition state which was optimised to higher level of accuracy, using the DFT functional. The results of these transition state investigations are shown in table 9.

Table 9: Comparison of am1 and DFT Diels Alder Transition states

	Semi empirical am1	DFT/6-31G(d)
Structure of TS
Energy (a.u.)	0.111629	-234.543896
Terminal C-C bond lengths (angstroms)	2.11917	2.27349
Imaginary Frequency (cm-1)	-955.45	-525.19
Frequency Animation	Vibration	Vibration

Molecular orbital analysis of Transition State

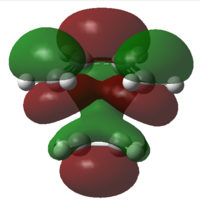
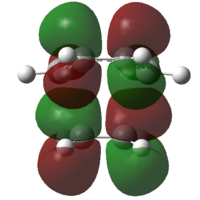
In order to confirm the fact that the symmetry of molecular orbitals allow a reaction to occur or forbid it from occurring, it is possible to analyse the molecular orbitals of the transition states. Both the HOMO and the LUMO orbitals for the transition states using both methods are shown in table 10.

Table 10: HOMO and LUMO orbitals for transition structure

	Semi-empirical AM1		DFT - TS (Berny)
	HOMO	LUMO	HOMO	LUMO
Molecular Orbital

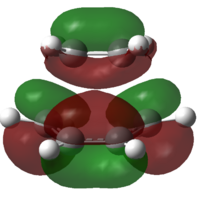It can be deduced from the molecular orbitals of the reactants the make up of the transition state HOMO's and LUMO's.
am1 HOMO: Ethylene LUMO and butadiene HOMO
am1 LUMO: Ethylene HOMO and butadiene LUMO
DFT HOMO: Ethylene HOMO and butadiene LUMO
DFT LUMO: Ethylene LUMO and butadiene HOMO

The difference between the HOMO's and the LUMO's in these diagrams is that the HOMO's have in phase interactions between the reactants whilst the LUMO's have out of out of phase interactions. Even though two of these orbitals are antisymmetric overall, the orbitals do confirm that only orbitals of the same symmetry can make up molecular orbitals.

Reaction of Maleic Anhydride with cyclohexa-1,3-diene

Another Diels Alder reaction that can be studied in a similar manner to those above is the reaction of cyclohexa-1,3-diene with maleic anhydride. This reaction is different to those aove because of the fact that it can produce structurally different exo- and endo- products. These two products of this reaction along with the mechanism are shown in figure 13.

Figure 13 - Mechanism for Reaction between Maleic Anhydride and Cyclohexa-1,3-diene

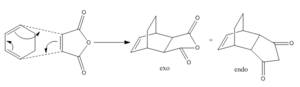
The endo product will predominate in this reaction as the endo transition state is lower in energy than the exo transition state.

Molecular orbital interactions

As with the Diels Alder reaction above, it is possible to analyse the molecular orbitals of the reactants in order to prove the theory that only orbitals of the same symmetry interact. In this reaction it would be predicted that the HOMO of cyclohexa-1,3-diene and the LUMO of maleic anhydride would interact as the cyclohexa-1,3-diene molecule would be the electron rich species in the reaction, acting as the equivalent of the diene in the Diels Alder reaction. The HOMO and LUMO molecular orbitals of both reactants are shown in table 11. This have been produced using the am1 level of theory.

Table 11: HOMO and LUMO orbitals of cyclohexa-1,3-diene and maleic anhydride

	cyclohexa-1,3-diene	maleic anhydride
HOMO
LUMO

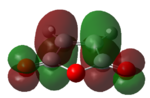These molecular orbital diagrams show that the LUMO of the cyclohexa-1,3-diene and the HOMO of maleic anhydride are symmetric (in the case of cyclohexa-1,3-diene only roughly symmetric, due to the lack symmetry in the actual molecule), whilst the HOMO of the cyclohexa-1,3-diene and the LUMO of maleic anhydride are unsymmetrical. This symmetry backs up the view that the HOMO of the cyclohexa-1,3-diene should interact with the LUMO of the maleic anhydride as it is symmetrically allowed.

Locating a transition state

These optimised structures could then be used in order to find a transition state for this Diels Alder reaction. This was done by arranging the molecules into both the endo and exo conformations and running both am1 and DFT level of theory calculations.

Table 12: Comparison of am1 and DFT for exo structured transition state

	Semi empirical am1	DFT/6-31G(d)
Structure of TS
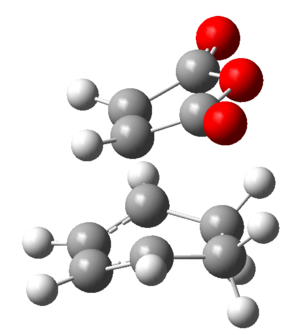Energy (a.u.)	-0.05042	-612.67931
Terminal C-C bond lengths (angstroms)	2.17043	2.29181
Imaginary Frequency (cm-1)	-812.09	-448.81
Frequency Animation	Vibration	Vibration

Table 13: Comparison of am1 and DFT endo transition state

	Semi empirical am1	DFT/6-31G(d)
Structure of TS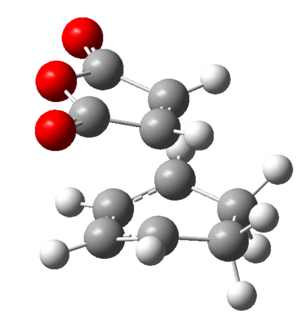
Energy (a.u.)	-0.05150	-612.68340
Terminal C-C bond lengths (angstroms)	2.16194	2.26903
Imaginary Frequency (cm-1)	-806.36	-447.06
Frequency Animation	Vibration	Vibration

Transition state MO analysis

It is then possible to analyse the molecular orbitals of the transition state in order to confirm that they are made up of a combination of either 2 symmetrical or 2 non-symmetrical reactant molecular orbitals. These molecular orbitals are in table14, found using the semi empirical am1 method.

Table 14: Molecular orbitals of transition state structures

	endo		exo
	HOMO	LUMO	HOMO	LUMO
Molecular Orbital

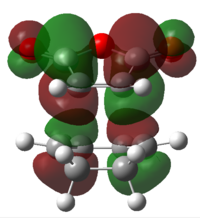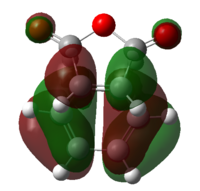The result of this MO analysis do not show a great deal of difference between the HOMO of the endo structure and the HOMO of the exo structure, therefore meaning that it is not possible to understand the greater stability of the endo transition state from these HOMO orbitals alone. The situation is unfortunately the same in the case of the LUMO orbitals.

Conclusion

In conclusion the techniques used in this investigation have been very useful in determining transition states of molecules. These techniques have also allowed one to compare the structures in different levels of theory, therefore proving that certain computational techniques are more accurate than others.