Rep:Mod:enricof11inorg

Written by Enrico Fantoni on 10.2010

Module 2 Inorganic Computational Laboratories

Intro

Computational chemistry is becoming an always more powerful tool to predict and support experimental data. In this report, we focus on the inorganic aspects of computational chemistry, especially concerning the use of energy optimisation tools, MOs, larger basis sets, NBOs and vibrations for elements involved in inorganic processes.

TlBr3

Studying the energy optimisation of TlBr3 computationally -using Gaussian- reveals that the most energetically stable conformation of the molecule is that in which:

the Tl-Br distance is 2.782Å (lit.2.69Å for TlI3. Reasonable result.)
the Br-Tl-Br angle is 120.0°

The calculation was carried out using the "medium" basis set LanL2MB, calculation method RB3LYP and calc.type FOPT. Convergence was achieved at -91.160 a.u.
To access the log file: https://www.ch.imperial.ac.uk/wiki/images/8/80/Ef108_TlBr3_opt.txt

Is this optimisation correct? We can double check by carrying out a frequency analysis using the same basis set and method, so that the two calculations are comparable. This is like finding the second derivative of the potential energy surface. Since, in this instance, all vibrations are positive, it confirms that the structure has been correctly optimised, as we have achieved a minimum in energy (as opposed to a maximum).

The low frequencies, i.e. the motions of the centre of mass, are ok but not excellent, since they are 1 order of magnitude smaller than the smaller "real" normal mode 41cm^-1. This is because the basis set adopted is not highly precise:

---Low frequencies (cm-1) -0.92 -0.005 -0.001 0.01 4.20 4.20
---Low frequencies (cm-1) 41 41 43 143 199 199

Note: In some instances, the image of the molecule appears without bonds only because the bond length is over a certain limit by which Gaussview classifies what is a "bond" and what is not. Bonds in gaussview are more of a visual aid to identify an existing interaction between two atoms, as the program "sees" the electrons involved in the interaction regardless of whether the interaction is labelled as "bond".

BH₃

In order to study the vibrations of BH₃, we submit a frequency job (http://hdl.handle.net/10042/to-5276) and gaussian is then able to show us that:

Vibrations of BH₃

number	form of the vibration	description of the vibration	frequency (cm-1)	intensity	symmetry D3h point group
1		The Hs move in and out of the z axis, B is stationary	1144	93	A2 translation along the z axis
2		2 Hs move away and towards the 3rd H, the 3rd H and B are stationary	1204	12	E' translation along y axis
3		B is stationary, 2 Hs rotate symmetrically around B, the 3rd H moves right/left with respect to the plane between the otehr 2 Hs and B.	1204	12	E' translation in the xy plane
4		All Hs move together outwards, B is stationary	2600	0	A1' totally symmetric
5		One H and B are stationary, the other two Hs move antisimmetrically towards and away from B	2700	104	E' translation in the xy plane
6		All Hs move towards/away from B, 2 of them symmetrically, the 3rd anti-symmetrically. B is stationary	2700	104	E' translation in the xy plane

The IR spectrum appears as follows. Only 3 peaks are present as 2 pairs of vibrational states are degenerate. Vibrations are assigned directly on the spectrum. Vibration 4 has 0 intensity, so it doesn't appear in the spectrum

MO analysis for BH₃

One of the features of calculating the electronic structure of BH3 with Gaussian is the possibility of viewing graphically the shape of the calculated MO. In the following section we compare the calculated MO with the theoretically predicted ones.

The MO of BH3 is as follows.

We can now compare the theoretically predicted MOs with the calculated ones.

The MOs above display excellent similarity! Some slight distortion of the electronic cloud can be noticed in the LUMO+2 and +3, to allow for the antibonding interactions to spread out. Overall, this match confirms the excellent validity and accuracy of qualitative MO theory.

Calculations on the isomers of Mo(CO)₄L₂

Three optimisations were necessary to obtain a stable structure for the molybdenum complex:

Optimisation 1 (basis set B3LYP, ECP LANL2MB, loose): cis --> http://hdl.handle.net/10042/to-5326 trans --> http://hdl.handle.net/10042/to-5329

Optimisation 2 (basis set B3LYP, ECP LANL2DZ, ultrafine): cis --> http://hdl.handle.net/10042/to-5335 trans --> http://hdl.handle.net/10042/to-5336

Optimisation 3 (D function for P added): cis --> http://hdl.handle.net/10042/to-5342 trans --> http://hdl.handle.net/10042/to-5341

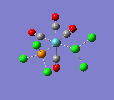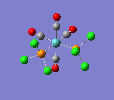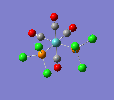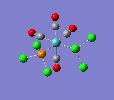
Finally, the optimised final structures are as follows:

Data on cis and trans [Mo(CO)4(PCl3)2] (all bond lengths are in Å)

	cis-[Mo(CO)4(PCl3)2]	trans-[Mo(CO)4(PCl3)2]	literature(std.deviation)
Mo-axialC	2.05	2.06	2.109
Mo-equatorialC	2.02	2.06	2.109
Mo-PCl3	2.48	2.42	2.462(0.046)
P-Cl	2.12	2.12	2.1
axial C-O	1.17	1.17	1.2
P-Mo-P	94.3°	176.7°
closest alignment of a Cl to the axial ligands (dihedral angle)	6.9°	31.3°
Mo-P-Cl	ranges from 116 (Cls with largest dihed. angle with axial CO) to 119° (Cl with smallest dihed. angle with axial CO)	ranges from 117 (Cls with largest dihed. angle with axial CO) to 120° (Cl with smallest dihed. angle with axial CO)

The literature values above are useful to suggest that the computational calculations gave reasonable results.

The cis isomer displays a slight angular distortion of the two trans COs, which are no more exactly 180&deg (as in the trans isomer); but more 178.6°, bent away from the PCl3s electron clouds. Moreover, a chlorine of the PCl3 group likes to be pretty much aligned to the axial ligands, but with a slight angular torsion. Also, the Mo-C distance is shorter for carbonyl groups trans to the PCl3 groups, due to the EW trans effect of the latter group.

An other interesting peculiarity that applies to both isomers is that the closer the dihedral angle Cl-P-Mo-CO is to 0°, the larger is the angle Mo-P-Cl. This is most probably due to steric factors, which require the chlorines to get more distant to CO the more the angle between the two is decreased.

Concerning energy optimisation, the optimised structures have relative energies of -623.693au = 1637506.1 kJ/mol for the cis isomer and 623.694au = 1637508.7 kJ/mol for the trans one. Therefore, the cis isomer is slightly more stable – by 2600 J/mol - than the trans. This is possibly because of the possibility of distorting more the angle of the other Mo ligands to accommodate the PCl3 groups and, effectively, lower the energy of the complex. On the other hand, in the trans compound this distortion is limited by the presence of the other PCl3 group in the trans position (i.e. if a distortion favoured sterically one PCl3 group, it would anyway disfavour the other).

If we wanted a more stable trans than a cis, we could modify the PCl3 group with bulkier groups (PPh3, P^tBu3, ), which would create some steric clash in the cis isomer, leaving the trans relatively more stable.

The vibrational analysis suggests that the structures obtained are optimised at the minimum energy as they do not contain large negative low vibrations.

Low frequencies --- -1.3097 0.0002 0.0004 0.0008 0.7875 1.9594 Low frequencies --- 11.7714 20.2901 45.8838

There is 1 order of magnitude difference between the low and the high frequencies. The optimisation is not great but has succeeded.

Frequency calculations: cis --> http://hdl.handle.net/10042/to-5348 trans --> http://hdl.handle.net/10042/to-5400

Low vibrations of Mo complex

trans complex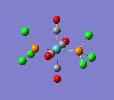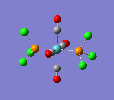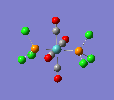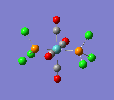
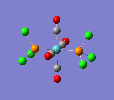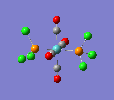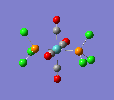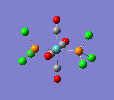cis complex

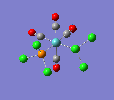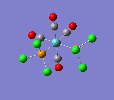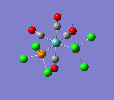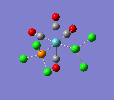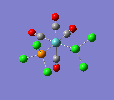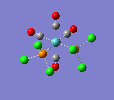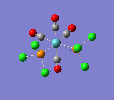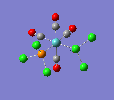At room temperature the molecule is quickly switching from a rotational state to another, as the energy needed to access such a state is minimal. IR of cis-complex's C=O: v/cm-1: 1952.36 (all CO asymm stretch), 1941.45 (cis CO stretch), 1938.17 (trans CO stretch), 2019.17 (all CO symm stretch). (Literature: 1899, 1911, 1929, 2023 cm-1).

IR of trans-complex's C=O: v/cm-1: 1937.79 (equatorial CO stretch), 1939.01 (axial CO stretch), 1966.70 (all CO asymm stretch), 2025.36 (all CO symm stretch).(Literature: 1902 cm-1, 1 band).

The number of bands doesn't correspond to that predicted from symmetry. Symmetry would predict that we have 1 CO stretching band for the trans complex (all COs are equal) while there would be 4 bands for the cis complex, due to the trans effect of the PCl3 ligands. However, here we do not see a one single band for the trans complex, probably as the computational calculation is able to distinguish between the 4 trans carbonyls so it sees them as 4 different environments, hence 4 stretches.

Vibrational spectrum of the trans complex

Vibrational spectrum of the cis complex

To visit the wikipage of the miniproject on adamantane follow the link -------> https://www.ch.imperial.ac.uk/wiki/index.php/Imprj:adamantane