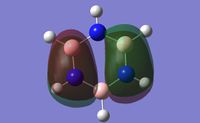
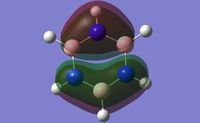
Rep:Mod:emf2407
Gaussian Optimisation Calculations
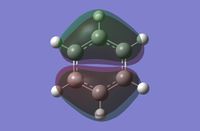
Optimised Structure of BH3
A molecule of BH3 was optimised using GaussView to find its lowest energy optimised geometry. The symmetry of the molecule was not constrained throughout the calculation and the three bonds were all altered to different lengths before the calculation. The lengths chosen were 1.53 A, 1.54 A, and 1.55 A respectively. This was to break molecular symmetry of the original planar structure.
The optimisation solves the Schrodinger equation for the electronic density and the energy, then for the position of the nuclei. This involves moving the nuclei to different positions and comparing the changed energy to find the lowest energy geometry.
The first optimisation calculation was done using the method: B3LYP, with the basis set: 3-21G. This method determines type of approximations. The basis set of 3-21G is quite low accuracy, but results in a very fast calculation.
| Parameter | Data |
|---|---|
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| Final Energy (a.u.) | -26.4622643 |
| Gradient (a.u.) | 0.00008851 |
| Dipole Moment (D) | 0.00 |
| Point Group | CS |
| Calculation Time (s) | 30.0 |
The calculation is complete as the gradient is very close to 0 (0.00008851), as well as the output code validating that the forces converged, and a stationary point in the geometry energy has been found.
Item Value Threshold Converged?
Maximum Force 0.000220 0.000450 YES
RMS Force 0.000106 0.000300 YES
Maximum Displacement 0.000940 0.001800 YES
RMS Displacement 0.000447 0.001200 YES
Predicted change in Energy=-1.672479D-07
Optimization completed.
-- Stationary point found.
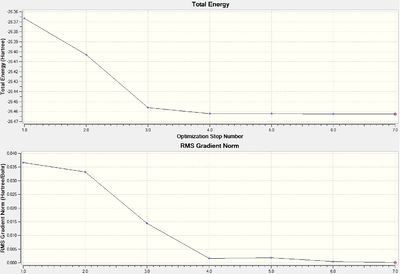
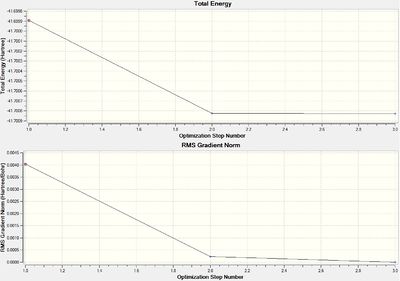
The two graphs shown above in figure 1, summarise how the energy and gradient of the molecule have changed through the optimisation. It shows that it took seven steps to find the lowest Energy and RMS Gradient geometry, a relatively high number due to the manual reduction in symmetry and the low accuracy basis set.
Summary of the optimised structure of BH3:
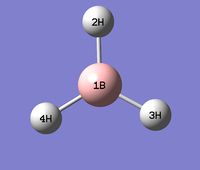
| Bond Length (A) | H-B-H Bond Angle (Degrees) | |
|---|---|---|
| 1B - 2H | 1.19 | 120.0 |
| 1B - 3H | 1.19 | 120.0 |
| 1B - 4H | 1.19 | 120.0 |
| Average | 1.19 | 120.0 |
Energy : -26.4622643 a.u. (7 d.p.)
The symmetry of the molecule was expected to be D3h however the calculation has come out with CS symmetry due to slight differences in each of the bond lengths and angles, which reduce the symmetry. This is a combined factor of the manual bond setting prior to the calculation (which removed symmetry) as well as very small inaccuracies in x, y, z coordinates. The CS symmetry has come out as the mirror symmetry was not manually broken.
The optimisation was then repeated using the 3-21G optimised file, and a more accurate basis set: 6-31G(d,p), to give a better result of the optimised structure. This allows a study of the effects of using different basis sets.

| Parameter | Data |
|---|---|
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -26.6153236 |
| Gradient (a.u.) | 0.00000706 |
| Dipole Moment (D) | 0.00 |
| Point Group | CS |
| Calculation Time (s) | 321.0 |
Item Value Threshold Converged?
Maximum Force 0.000012 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.000061 0.001800 YES
RMS Displacement 0.000038 0.001200 YES
Predicted change in Energy=-1.068574D-09
Optimization completed.
-- Stationary point found.
| Bond Length (A) | H-B-H Bond Angle (degrees) | |
|---|---|---|
| 1B - 2H | 1.19 | 120.0 |
| 1B - 3H | 1.19 | 120.0 |
| 1B - 4H | 1.19 | 120.0 |
| Average | 1.19 | 120.0 |
Energy : -26.6153236 a.u.
The energies of the two basis sets are considerably different but cannot be compared due to different approximations made in each calculation.
The bond angles are all very similar with plus/minus fluctation of 0.006 around the ideal value of 120 degrees, as the calculated values are accurate to 0.1 d.p. all angles come out at the idealised 120 degrees.
The bond lengths attained from this basis set are slightly lower than the previous, but to the level of accuracy of 0.01 A, all values are still the same. The bond lengths are similar to the literature value of 1.185 A[1]. This second estimate is slightly closer, taking into account more significant figures, meaning this basis set gave a slightly better result aligning with experimental.
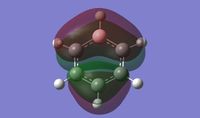
Optimised Structure of GaBr3
A molecule of GaBr3 was optimised to find the lowest energy geometry using GaussView. The molecule was constrained to the D3h point group throughout the optimisation, and given very tight (0.0001) tolerance.
The optimisation was run with calculation method: B3LYP, basis set: LanL2DZ. It uses D95V (medium basis set) on first row atoms, and Los Alamos ECP on heavier elements. This pseudo potential is required due to the high molecular weight of Gallium, where the atom consists of core electrons and valence electrons. This allows the program to assume that the valence electrons dominate in bonding interactions, and the core electrons can be modelled by a pseudo-potential.
| Parameter | Data |
|---|---|
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| Final Energy (a.u.) | -41.7008278 |
| Gradient (a.u.) | 0.00000016 |
| Dipole Moment (D) | 0.00 |
| Point Group | D3H |
| Calculation Time (s) | 13.8 |
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000003 0.001800 YES
RMS Displacement 0.000002 0.001200 YES
Predicted change in Energy=-1.282693D-12
Optimization completed.
-- Stationary point found.
Optimised Structure of GaBr3:

| Bond Length (A) | Br-Ga-Br Bond Angle (Degrees) | |
|---|---|---|
| 1Ga - 2Br | 2.35 | 120.0 |
| 1Ga - 3Br | 2.35 | 120.0 |
| 1Ga - 4Br | 2.35 | 120.0 |
| Average | 2.35 | 120.0 |
Energy : -41.7008278 a.u.
Due to the symmetry point group constraint of D3h all bond lengths and angles came out to be equal, this is because any difference in the three lengths and angles would cause a break in the symmetry of the molecule and therefore the point group would change.
The bond length for Ga-Br in GaBr3 is 2.3525 A in the gas phase[2]. This has come out very similar to the Gaussian calculated value of 2.35 A, showing that this method and basis set are highly accurate for the optimisation of this molecule.
Optimised Structure of BBr3
A molecule of BBr3 was optimised using a different technique in terms of basis sets. The optimisation was done using calculation method: RB3LYP, and basis set: GEN. This basis set option allow the basis set for each atom of the molecule to be individually set. The keyword 'pseudo=read gfinput' was added to allow pseudo potentials to be individually set for each atom.
The file for this calculation was edited to assign the boron atom as full basis set 6-31G(d,p), and the bromine atoms as pseudo potentials LanL2DZ (due to the high molecular weight).

| Parameter | Data |
|---|---|
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | Gen |
| Final Energy (a.u.) | -64.4364490 |
| Gradient (a.u.) | 0.00000962 |
| Dipole Moment (D) | 0.00 |
| Point Group | CS |
| Calculation Time (s) | 20.7 |
Item Value Threshold Converged?
Maximum Force 0.000017 0.000450 YES
RMS Force 0.000010 0.000300 YES
Maximum Displacement 0.000107 0.001800 YES
RMS Displacement 0.000062 0.001200 YES
Predicted change in Energy=-2.170129D-09
Optimization completed.
-- Stationary point found.
Optimised Structure of BBr3:

| Bond Length (A) | Br-B-Br Bond Angle (Degrees) | |
|---|---|---|
| 1B - 2Br | 1.93 | 120.0 |
| 1B - 3Br | 1.93 | 120.0 |
| 1B - 4Br | 1.93 | 120.0 |
| Average | 1.93 | 120.0 |
Energy : -64.4364490 a.u.
The average optimised B-Br bond distance was calculated to be 1.93 A. This is close to the literature value of 1.9004 A[3] (from gaseous electron diffraction), meaning the basis sets and approximations made in the calculation have a good level of accuracy.
The optimised Br-B-Br Bond Angle averaged as 120.0 degrees, expected for this symmetric, trigonal planar molecule. Small fluctuations around this ideal value, to a greater number of decimal places result from small inaccuracies in the calculation.
Comparative Discussion
| Molecule | Average Bond Length (A) | Average Bond Angle (Degree) |
|---|---|---|
| BH3 | 1.19 | 120.0 |
| GaBr3 | 2.35 | 120.0 |
| BBr3 | 1.93 | 120.0 |
All three molecules have the same bond angles of 120.0 degrees, this is due to the trigonal planar arrangement of the ligands around the sp2 centre. The ligands are held with maximum distance in between them minimising any possible repulsions. Both Boron and Gallium are in group 3, and hence with three ligands are electron deficient overall. This means there is a free p orbital which can be used to accept electron density and alleviate electron deficiency.
BH3 has the lowest bond length of the three molecules due to the small size and low electronegativity of the hydrogen atom. It can be held at a relatively close distance to the boron due to a lack of high atomic repulsion, due to the nature of the hydrogen ligand. The electronegativity of boron and hydrogen are very similar (X = 2.0, and 2.1[4] respectively) and result in good overlap between orbitals, and low bond polarity and therefore stronger, shorter bonds. Changing the hydrogen ligands to bromine atoms causes an increase in the bond length. The first reason is the bromine ligands are significantly larger than the hydrogen ligands, and nuclear repulsion is much higher - hence the bromine atoms are held further from the central core. The bromine ligands are also more electronegative (X = 2.8) than the hydrogen, resulting in more mismatched orbitals, worse overlap with the central atom, and considerably more polar bonds. This overall results in weaker, longer bonds. The bromine atoms are large and electron rich, with 3 lone pairs which are able to interact with the empty p orbital of the central atom, this increases the bond order of the ligand and results in a stronger, contracted bond.
GaBr3 has the largest bond length, (Ga X = 1.6) the bromine atoms and the gallium are both high molecular weight with a significant amount of electron density between the central nuclei, this leads to a certain level of repulsion between the two large centres which overall increases the equilibrium distance. The bonds between the ligand and the central atom are also much more polar due to the electronegativity difference, resulting in higher energy, longer bonds.
Gaussian does not draw in expected bonds for some structures in the optimisation process. This does not mean that a bond is not present between the two atoms, merely that the distance between the atoms is higher than the Gaussian 'limit' for the physical depiction of a chemical bond.
One of the first major chemists to fully classify a chemical bond was Linus Pauling, who defined it to be formed when the forces acting between two atoms lead to "formation of an aggregate with sufficient stability ... to consider it as an independent species"[5]. IUPAC extends this definition with the addition of bond characteristics, principally the existence of an inter-nuclear region where potential energy can drastically improve by atomic contraction with a small increase in kinetic energy. This is a general characterisation which is applicable to covalent bonds, ionic bonds, as well as weaker bonds[6].
Gaussian Frequency Calculations
BH3 Frequency
Vibrational analysis is used to confirm that the optimised structures are minimum energy. This frequency calculation was done using the 6-31G(d,p) BH3 fully optimised structure.
| Parameter | Data |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -26.6153236 |
| Gradient (a.u.) | 0.00000704 |
| Dipole Moment (D) | 0.00 |
| Point Group | CS |
| Calculation Time (s) | 13.0 |
Item Value Threshold Converged?
Maximum Force 0.000014 0.000450 YES
RMS Force 0.000007 0.000300 YES
Maximum Displacement 0.000088 0.001800 YES
RMS Displacement 0.000045 0.001200 YES
Predicted change in Energy=-1.479043D-09
Optimization completed.
-- Stationary point found.
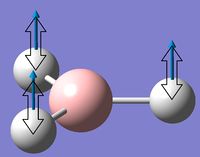
Low frequencies --- -25.0262 -12.9599 -0.0010 -0.0003 0.0000 15.1275 Low frequencies --- 1162.9971 1213.0313 1213.1466
The low frequencies relate to the vibrational frequencies of the molecule, 3N - 6 (non-linear) . The six low frequencies above are the equivalent to the '- 6' in the equation, relating to the centre of mass motion. For this case two of the six, 'zero' frequencies are quite high: - 25 and + 15. For a good frequency calculation all of the six must be very close to 0. These break the limits of plus/minus 15 cm-1, most likely due to the lower symmetry of the Cs point group compared to D3h.
Hence the molecular point group was constrained to D3h symmetry and this frequency calculation was repeated - resulting in much lower 'zero' frequencies of the molecule, as shown below:
| Parameter | Data |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -26.6153236 |
| Gradient (a.u.) | 0.00000526 |
| Dipole Moment (D) | 0.00 |
| Point Group | D3H |
| Calculation Time (s) | 5.0 |
Item Value Threshold Converged?
Maximum Force 0.000011 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000041 0.001800 YES
RMS Displacement 0.000021 0.001200 YES
Predicted change in Energy=-6.531237D-10
Optimization completed.
-- Stationary point found.
Low frequencies --- -4.8516 -1.2089 -0.0054 1.0196 9.0970 9.1770 Low frequencies --- 1162.9788 1213.1708 1213.1735
The low frequencies are in the range of plus/minus 10 which corresponds to a reasonable method used for the calculation.
Gaussian can next be used to animate the calculated vibrations to give visual interpretation of the vibrational frequencies of the molecule. The six vibrations are shown in the table below for the D3h BH3 molecule analysed above.
IR Spectrum:

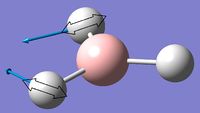
In order for a vibration to give a peak on an IR spectrum it must have a permanent dipole moment. There are six vibrations calculated for the BH3 molecule but only 3 visible peaks on the IR spectrum. Vibration 4 is a completely symmetric stretch, the forces cancel out due to equal magnitude, this means there is no permanent dipole within the vibration, and hence is not observed on the spectrum. Vibrations 2 and 3, and 5 and 6 are respectively degenerate and therefore appear at the same point on the spectra, meaning only two distinct peaks are observed rather than four. Together this gives rise to three peaks.
GaBr3 Frequency
The frequency calculations were then done for the optimised GaBr3 molecule to confirm the structure is a minimum.
| Parameter | Data |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| Final Energy (a.u.) | -41.7008278 |
| Gradient (a.u.) | 0.00000011 |
| Dipole Moment (D) | 0.00 |
| Point Group | D3H |
| Calculation Time (s) | 9.1 |
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000002 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-6.142863D-13 Optimization completed. -- Stationary point found.
Low frequencies --- -0.5252 -0.5247 -0.0024 -0.0010 0.0235 1.2010 Low frequencies --- 76.3744 76.3753 99.6982
The lowest real normal mode for this molecule is 76 cm-1.
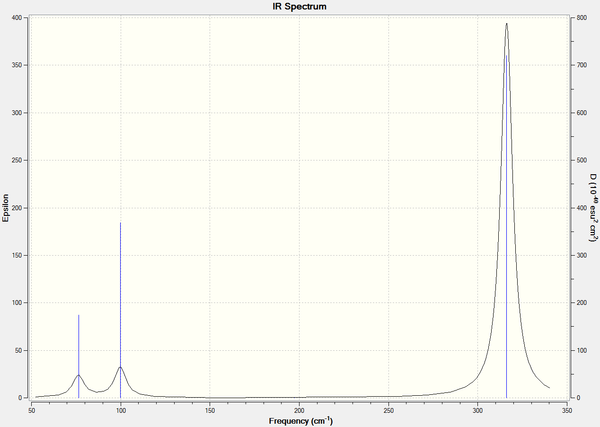
The IR spectrum for GaBr3 shown in figure 9, shows three peaks, the symmetric vibration once again IR inactive, and vibrations 1 and 2, and 5 and 6 are also degenerate similarly to BH3.
Comparative Vibrational Frequencies
| BH3 | GaBr3 | |||||
|---|---|---|---|---|---|---|
| Vibration Number | Frequency (cm-1) | Intensity | Symmetry D3h Point Group | Frequency (cm-1) | Intensity | Symmetry D3h Point Group |
| 1 | 1160 | 92 | A2" | 80 | 3 | E' |
| 2 | 1210 | 14 | E' | 80 | 3 | E' |
| 3 | 1210 | 14 | E' | 100 | 9 | A2" |
| 4 | 2580 | 0 | A1' | 200 | 0 | A1' |
| 5 | 2710 | 126 | E' | 320 | 57 | E' |
| 6 | 2710 | 126 | E' | 320 | 57 | E' |
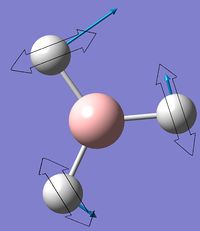
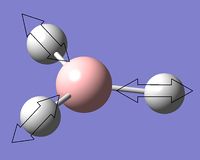
The symmetry point groups for the different vibrations for both GaBr3 and BH3 are overall the same - four E', A2", and A1'. This is a result of the molecules being the same point group with the same geometry, giving the vibrations the same symmetry overall. There has however been a reordering in the modes with the A2" mode for BH3 being lower energy than the two E' modes, compared to GaBr3 where this A2" is higher energy.
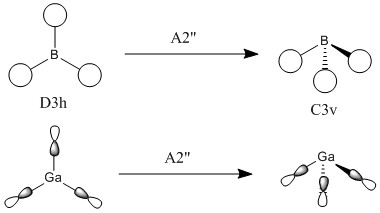
This can be rationalised by consideration of the forms of the vibrations. The significant difference in the two A2" modes is the motion of the central atom, where for BH3 the displacement of the boron is very low compared to the displacement of the Ga in GaBr3. One reason why this mode would be lower energy for BH3 would be to consider the bonding interactions of the ligands in the maximum displacement position - the symmetry has changed to C3v and interactions between the ligands are possible, as shown in figure 10. Due to shorter B-H bonds, the hydrogen atoms are closer together than the corresponding bromine atoms, hence more bonding interaction is possible to stabilise the mode and reduce its energy. Another factor to be taken into account are the valence p orbitals of bromine compared to s, p orbitals tend to be higher energy therefore interactions between them would be less stabilising compared to s orbital hydrogen interactions.
The frequency values are hugely different for the two molecules, with GaBr3 ranging between 75 - 315 cm-1, and BH3 1160 - 2715 cm-1. The frequency of an IR absorption is related to the force between the atoms (essentially bond strength) as well as the reduced mass of the atoms.[7] This is given by the equation:
Where c = speed of light, kf = force constant, reduced mass = m1m2 / (m1+m2)
This is a direct reflection of the bond strengths in the two molecules, where BH3 has considerably stronger bonds (as was previously indicated by the bond lengths). This was established to be due to the small, well-matched orbital sizes which result in strong overlap, as well as lower nuclear repulsion. The reduced mass is considerably larger for GaBr3 compared to BH3, which causes a reduction in the vibrational wavenumbers.
The IR spectra have very similar forms for each molecule, despite considerably different frequency values. Both graphs have high energy intense peaks corresponding to the higher energy degenerate E' modes, as well as two less intense lower energy peaks which are similar in energy to each other. This similarity is expected due to the molecules being the same point group with the same symmetry vibrational modes.
The higher energy modes which lie close together for both BH3 and GaBr3 (E', and A1') are much higher energy than the low energy modes due to the high level of bond length distortion caused by the vibration. For all the high energy modes on both molecules the vibration causes the ligand in some way to closely approach the central atom through bond shortening - this results in high repulsions which strongly increases the energy of these vibrations. All the low energy modes involve no bond shortening and all the ligands remain at a stable distance from each other, keeping repulsions low and the overall energy low.
The same method and basis sets are required for both the optimisation and frequency analysis calculations to allow direct comparisons to be made between molecules. Using a different method/basis set means that different assumptions are being made within the calculations and this can result in radically different results, but due to the nature of the underlying assumptions the results cannot be compared.
A frequency analysis is used to ensure that an optimised geometry for a molecule is a minimum. The calculation can only provide meaningful results at a stationary point of an energy curve, due to the second derivative calculations. If the frequency calculation gives results of very low frequencies (plus/minus 15 cm-1) and positive values for the real frequencies, it confirms the optimised structure is a minimum for the molecule.
The low frequencies represent motions of the centre of mass of the molecule, essentially the minus six of the 3N - 6 vibrational frequencies for non-linear molecules. These are required to be as close as possible to zero, a point corresponding to no overall change in the centre of mass for the molecule.
Gaussian Population Analysis
BH3 Analysis
The molecular orbitals of BH3 can also be computed using Gaussian. This is done with an Energy calculation, with the keyword: pop=full. This keyword switches the MO analysis on, and the full NBO calculation can then be run.
| Parameter | Data |
|---|---|
| File Type | |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -26.6153236 |
| Gradient (a.u.) | |
| Dipole Moment (D) | 0.00 |
| Point Group | CS |
| Calculation Time (s) | 22.7 |
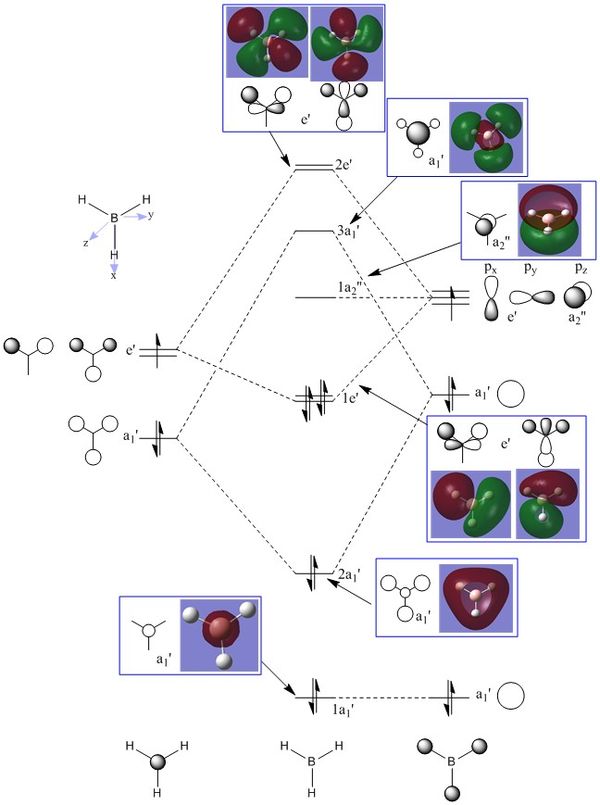
As can be seen in the above molecular orbital diagram (figure 11), the calculated molecular orbitals for BH3 are highly accurate when compared to the expected LCAOs. The red and green MO surface images correspond to the orbital phases highly accurately, with all LCAOs highly matched with their equivalent surface. The interface between the different coloured surfaces for the calculated MOs corresponds to the nodes between different phases of the LCAOs.
The one significant different between the LCAOs and the calculated MO images, is the size of the interactions. The LCAOs are highly localised to the orbitals of each atom of the molecule, resulting in obvious lacking in orbital interactions between atoms. The calculated MOs stretch across the whole molecule and can be considered to be delocalised within the framework of all the atoms.
NH3 Analysis
Optimisation:
This same analysis was then done for the NH3 molecule. The method and basis set used are the same as BH3 (B3LYP, 6-31G(d,p)) to allow direct comparison of resulting energies. The optimisation was done using keywords to give a good level of accuracy for the calculation: "opt=tight nosymm geom=connectivity int=ultrafine scf=conver=9".
| Parameter | Data |
|---|---|
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy (a.u.) | -56.5577687 |
| Gradient (a.u.) | 0.00000095 |
| Dipole Moment (D) | 1.85 |
| Point Group | C1 |
| Calculation Time (s) | 25.0 |
Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000005 0.000060 YES RMS Displacement 0.000003 0.000040 YES Predicted change in Energy=-9.687971D-12 Optimization completed. -- Stationary point found.
The very low value for the RMS gradient as well as the convergence of forces shows the optimisation is complete.
Frequency Calculation:
The optimised molecule was then used to undergo frequency analysis, to ensure the optimised structure is minimum energy.
| Parameter | Data |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy (a.u.) | -56.5577687 |
| Gradient (a.u.) | 0.00000095 |
| Dipole Moment (D) | 1.85 |
| Point Group | C1 |
| Calculation Time (s) | 11.0 |
Item Value Threshold Converged? Maximum Force 0.000002 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000005 0.001800 YES RMS Displacement 0.000002 0.001200 YES Predicted change in Energy=-1.088014D-11 Optimization completed. -- Stationary point found.
Low frequencies --- -6.5478 -4.7624 -0.0013 0.0014 0.0018 1.3376 Low frequencies --- 1089.3505 1693.9257 1693.9298
The low frequencies for this calculation have come out to be very low, showing the method used for the calculation to be accurate and a good approximation. The optimisation has reached the minimum energy form of the molecule.
Population Analysis:
Finally the optimised structure was used to carry out a population analysis to generate molecular orbitals for the molecule.
| Parameter | Data |
|---|---|
| File Type | .log |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy (a.u.) | -56.5577687 |
| Gradient (a.u.) | |
| Dipole Moment (D) | 1.85 |
| Point Group | C1 |
| Calculation Time (s) | 4.0 |


Natural Bond Orbital Analysis
Finally NBO analysis was carried out on the resulting NH3 molecule after the population analysis. The charge distribution of the molecule was visualised using NBO type option. The charge distribution is as expected for this molecule, as the highly electronegative nitrogen atom is negatively charge and the three hydrogen atoms are positively charged (using the colour charge range of -1.125 - 1.125).
The nitrogen atom has a charge of - 1.125, whilst each hydrogen atom has a charge of + 0.375. This charge distribution gives an overall charge of zero - expected for this neutral molecule. The atomic charges for each atom reflect the electronegativity differences. Nitrogen has a very high electronegativity, and is therefore able to strongly withdraw electron density from the weakly electronegative hydrogen atoms. As the nitrogen has three hydrogen molecules to withdraw electron density from it results in having a highly negative accumulative charge. The symmetry of the molecule is shown through each hydrogen having the same positive charge.
The NBO analysis can be further studied using the results file of this population analysis calculation. Below shows the individual atomic charges.
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
N 1 -1.12514 1.99982 6.11103 0.01429 8.12514
H 2 0.37505 0.00000 0.62250 0.00246 0.62495
H 3 0.37505 0.00000 0.62250 0.00246 0.62495
H 4 0.37505 0.00000 0.62250 0.00246 0.62495
=======================================================================
* Total * 0.00000 1.99982 7.97852 0.02166 10.00000
The section below describes the bonding in the molecule, where the nitrogen bonding orbitals are sp3 (as 75% p and 25% s), and the hydrogen bonding orbital is 100% s. The occupancy and the bond orbitals show that the bonds are 2 centre 2 electron between nitrogen and hydrogen with ca. 69% of the bond formed from the nitrogen orbital. Orbital four is the core s electrons of the nitrogen, and orbital five is the lone pair contained within an sp3 orbital on the nitrogen.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99909) BD ( 1) N 1 - H 2
( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%)
-0.0001 -0.4986 -0.0059 0.0000 -0.2910
0.0052 0.8155 0.0277 0.0000 0.0000
0.0281 0.0000 0.0000 0.0032 0.0082
( 31.17%) 0.5583* H 2 s( 99.91%)p 0.00( 0.09%)
-0.9996 0.0000 0.0072 -0.0289 0.0000
2. (1.99909) BD ( 1) N 1 - H 3
( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%)
0.0001 0.4986 0.0059 0.0000 0.2910
-0.0052 0.4077 0.0138 0.7062 0.0240
0.0140 0.0243 0.0076 0.0033 0.0031
( 31.17%) 0.5583* H 3 s( 99.91%)p 0.00( 0.09%)
0.9996 0.0000 -0.0072 -0.0145 -0.0250
3. (1.99909) BD ( 1) N 1 - H 4
( 68.83%) 0.8297* N 1 s( 24.86%)p 3.02( 75.05%)d 0.00( 0.09%)
0.0001 0.4986 0.0059 0.0000 0.2909
-0.0052 0.4077 0.0138 -0.7062 -0.0240
0.0140 -0.0243 -0.0076 0.0033 0.0031
( 31.17%) 0.5583* H 4 s( 99.91%)p 0.00( 0.09%)
0.9996 0.0000 -0.0072 -0.0145 0.0250
4. (1.99982) CR ( 1) N 1 s(100.00%)
1.0000 -0.0002 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
5. (1.99721) LP ( 1) N 1 s( 25.38%)p 2.94( 74.52%)d 0.00( 0.10%)
0.0001 0.5036 -0.0120 0.0000 -0.8618
0.0505 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 -0.0269 0.0155
The analysis below gives the mixing between any MOs in the molecule. This is empty for NH3 as mixing does not occur between MOs.
Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
The analysis below states the energy and occupancy of the N-H bonds, as well as stating the core electrons of the nitrogen and the lone pair.
Natural Bond Orbitals (Summary):
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (H3N)
1. BD ( 1) N 1 - H 2 1.99909 -0.60417
2. BD ( 1) N 1 - H 3 1.99909 -0.60417
3. BD ( 1) N 1 - H 4 1.99909 -0.60417
4. CR ( 1) N 1 1.99982 -14.16768
5. LP ( 1) N 1 1.99721 -0.31757
The N-H bonds have the same energy due to the high symmetry of the molecule. The nitrogen lone pair has higher energy than the bonding electrons most likely due to their more localised nature - with no positive nucleus to help stabilise. The core electrons of the nitrogen have significantly lower energy than the valence electrons, the reason why core electrons can be ignored on MO diagrams.
NH3BH3 Analysis

Ammonia-Borane is an acid-base complex, with a dative bond formed from the nitrogen lone pair to the boron empty p orbital. These two electrons are shared between the boron and nitrogen. The energy of this dative bond can be calculated using Gaussian. The association reaction of NH3 and BH3, as shown in figure 14, can be used to compute the reaction energy (essentially dative bond energy) on forming this complex.
Ammonia-borane was optimised using Gaussian with the same method and basis set as NH3 and BH3 (B3LYP, 6-31G(d,p)), to allow the energies to be compared. Keywords were used to ensure the minimum energy form was an accurate result: opt=tight nosymm geom=connectivity int=ultrafine scf=conver=9.
| Parameter | Data |
|---|---|
| File Type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy (a.u.) | -83.2246891 |
| Gradient (a.u.) | 0.00000122 |
| Dipole Moment (D) | 5.56 |
| Point Group | C1 |
| Calculation Time (s) | 67.0 |
Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000024 0.000060 YES RMS Displacement 0.000010 0.000040 YES Predicted change in Energy=-8.754453D-11 Optimization completed. -- Stationary point found.
Frequency Analysis
Frequency analysis was then done on the optimised ammonia-borane structure to ensure the optimised structure is minimum energy.
| Parameter | Data |
|---|---|
| File Type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy (a.u.) | -83.2246891 |
| Gradient (a.u.) | 0.00000131 |
| Dipole Moment (D) | 5.56 |
| Point Group | C1 |
| Calculation Time (s) | 32.0 |
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000024 0.001800 YES RMS Displacement 0.000010 0.001200 YES Predicted change in Energy=-1.172727D-10 Optimization completed. -- Stationary point found.
Low frequencies --- -3.2132 -2.7614 -0.0007 0.0013 0.0015 3.7326 Low frequencies --- 263.3416 632.9622 638.4409
The energy values for the optimisation and the frequency calculation are the same, showing the same geometry optimised form is used. The six 'zero' frequencies are very close to zero, within plus/minus four, reflecting the good method and basis set used. There are no negative frequencies , therefore the structure is the optimised, lowest energy.
Energy Summary
| Molecule | Energy (a.u.) |
|---|---|
| NH3 | -56.5577687 |
| BH3 | -26.6153236 |
| NH3BH3 | -83.2246891 |
The association energy for this reaction can now be calculated using the relative energy difference between the product and reactants, the relative energies can be compared as the same basis set and method have been used throughout:
This energy difference can now be converted to a more standard unit of kj/mol, using standard conversion factor:
This energy value is the association energy for the reaction, and can be subsequently be used to work out the dissociation energy, simply by reversing the sign, which is: + 135.47 kj/mol.
This is a sensible value for a bond dissociation energy. The bond energy of a molecule can vary greatly depending on the bond strength: a factor strongly dependent on bond polarity, and orbital size match. However most sigma bond strengths are in the order of 100 kj/mol[8]. So a "ballpark" value for this kind of heteronuclear first row bond would be around 100-200 kj/mol, taking into account the dative nature.
The value calculated above is very similar to the literature value of 130.1 kj/mol [9] showing the method and basis set used for the individual calculations have given rather accurate results in comparison to experimental data.
Aromaticity Project
Introduction

Aromatic compounds have huge significance in modern chemistry. The concept of aromaticity relates to the heightened stability of molecules with delocalised/conjugated electrons across a number of atoms, where the major requirements of this are: planar structure, and 4n + 2 delocalised electrons. Huckel's rule of aromaticity states the number of electrons required to show this stabilisation is 4n + 2 (where n = integer). This part of the project studies the properties and molecular orbitals of a range of isoelectronic molecules, each exhibiting a level of aromaticity. The classic example of an aromatic molecule is benzene, this common molecule will be the standard used in the comparisons. The molecules which will be compared to this are the isoelectronic molecules, pyridinium, boratabenzene, and borazine.
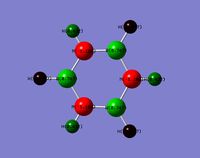
Benzene Analysis
A molecule of benzene was optimised using the method: B3LYP, and basis set: 6-31G(d,p). Keywords: opt=tight nosymm geom=connectivity int=ultrafine scf=conver=9
| Parameter | Data |
|---|---|
| File Type | |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -232.2582028 |
| Gradient (a.u.) | 0.00000839 |
| Dipole Moment (D) | 0.00 |
| Point Group | C1 |
| Calculation Time (s) | 292.2 |
Item Value Threshold Converged? Maximum Force 0.000011 0.000015 YES RMS Force 0.000004 0.000010 YES Maximum Displacement 0.000042 0.000060 YES RMS Displacement 0.000015 0.000040 YES Predicted change in Energy=-1.687646D-09 Optimization completed. -- Stationary point found.
The gradient above is very close to zero and the forces have converged, showing the optimum geometry has been calculated. All bond lengths are calculated to be 1.40 A, which is very close to the literature value of 1.39 A[10] .
Frequency Analysis
A frequency analysis was then done for the optimised molecule of benzene to ensure the result was a minimum in energy.
| Parameter | Data |
|---|---|
| File Type | |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -232.2582028 |
| Gradient (a.u.) | 0.00000823 |
| Dipole Moment (D) | 0.00 |
| Point Group | C1 |
| Calculation Time (s) | 629.3 |
Item Value Threshold Converged? Maximum Force 0.000021 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000044 0.001800 YES RMS Displacement 0.000019 0.001200 YES Predicted change in Energy=-1.736103D-09 Optimization completed. -- Stationary point found.
Low frequencies --- -8.0758 -3.7952 -3.4302 0.0002 0.0005 0.0009 Low frequencies --- 414.5374 414.5435 621.0493
The low frequencies shown above are within plus/minus 9, this shows the method and basis set suit the molecular calculation well. There are no negative frequencies, hence the optimised geometry is a minimum.
Population Analysis
Finally population analysis was done to obtain the full NBO set for benzene which can be used to compare subsequent isoelectronic molecules. The keyword: pop=full was used to allow calculation of the full set of molecular orbitals.
| Parameter | Data |
|---|---|
| File Type | |
| Calculation Type | |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -232.2582028 |
| Gradient (a.u.) | 0.00000823 |
| Dipole Moment (D) | 0.00 |
| Point Group | C1 |
| Calculation Time (s) |

The charge analysis shows the negatively charged carbon centres with the positively charged hydrogen atoms attached the charge is evenly distributed adhering to the molecular symmetry. The charge range shown is - 0.239 - + 0.239. The charge is completely symmetric for all atoms of the same element. The carbon is more positively charged due to its greater electronegativity compared to hydrogen, which has lost some electron density to carbon resulting in a positive charge.
The NBO can be further studied using Gaussian's computed data:
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
C 1 -0.23860 1.99910 4.22618 0.01331 6.23860
C 2 -0.23858 1.99910 4.22616 0.01331 6.23858
C 3 -0.23858 1.99910 4.22617 0.01331 6.23858
C 4 -0.23860 1.99910 4.22618 0.01331 6.23860
C 5 -0.23858 1.99910 4.22616 0.01331 6.23858
C 6 -0.23858 1.99910 4.22617 0.01331 6.23858
H 7 0.23859 0.00000 0.75998 0.00144 0.76141
H 8 0.23859 0.00000 0.75998 0.00144 0.76141
H 9 0.23859 0.00000 0.75998 0.00144 0.76141
H 10 0.23859 0.00000 0.75998 0.00144 0.76141
H 11 0.23859 0.00000 0.75998 0.00144 0.76141
H 12 0.23859 0.00000 0.75998 0.00144 0.76141
=======================================================================
* Total * 0.00000 11.99462 29.91690 0.08847 42.00000
The table above summarises the atoms of the molecule with their respective charges. It shows the presence of core electrons for the carbon atoms and the overall electron count of 42.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98098) BD ( 1) C 1 - C 2
( 50.00%) 0.7071* C 1 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 0.3027
-0.0226 0.7448 0.0277 0.0003 0.0000
0.0131 0.0000 0.0000 -0.0101 -0.0109
( 50.00%) 0.7071* C 2 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 -0.3404
-0.0356 -0.7283 -0.0023 -0.0002 0.0000
0.0111 0.0000 0.0000 -0.0123 -0.0109
2. (1.98098) BD ( 1) C 1 - C 6
( 50.00%) 0.7071* C 1 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 0.4605
-0.0158 -0.6590 -0.0320 -0.0006 0.0000
-0.0162 0.0000 0.0000 -0.0034 -0.0109
( 50.00%) 0.7071* C 6 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 -0.4937
-0.0353 0.6345 -0.0057 0.0006 0.0000
-0.0153 0.0000 0.0000 -0.0063 -0.0109
3. (1.66519) BD ( 2) C 1 - C 6
( 50.00%) 0.7071* C 1 s( 0.00%)p 1.00( 99.96%)d 0.00( 0.04%)
0.0000 0.0000 0.0000 0.0000 0.0005
0.0000 -0.0005 0.0000 0.9997 -0.0133
0.0000 0.0179 -0.0077 0.0000 0.0000
( 50.00%) 0.7071* C 6 s( 0.00%)p 1.00( 99.96%)d 0.00( 0.04%)
0.0000 0.0000 0.0000 0.0000 0.0005
0.0000 -0.0005 0.0000 0.9997 -0.0133
0.0000 -0.0020 0.0194 0.0000 0.0000
4. (1.98306) BD ( 1) C 1 - H 7
( 62.04%) 0.7877* C 1 s( 29.57%)p 2.38( 70.39%)d 0.00( 0.04%)
0.0003 -0.5437 -0.0126 0.0010 0.8336
-0.0145 0.0937 -0.0016 -0.0003 0.0000
-0.0037 0.0000 0.0000 -0.0162 0.0105
( 37.96%) 0.6161* H 7 s( 99.95%)p 0.00( 0.05%)
-0.9997 -0.0014 -0.0226 -0.0025 0.0000
5. (1.98098) BD ( 1) C 2 - C 3
( 50.00%) 0.7071* C 2 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 0.7963
0.0127 0.1103 0.0334 -0.0003 0.0000
0.0022 0.0000 0.0000 0.0164 -0.0109
( 50.00%) 0.7071* C 3 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 -0.8009
-0.0198 -0.0694 0.0297 0.0003 0.0000
0.0052 0.0000 0.0000 0.0158 -0.0109
6. (1.66518) BD ( 2) C 2 - C 3
( 50.00%) 0.7071* C 2 s( 0.00%)p 1.00( 99.96%)d 0.00( 0.04%)
0.0000 0.0000 0.0000 0.0000 0.0005
0.0000 -0.0005 0.0000 0.9997 -0.0133
0.0000 0.0178 -0.0079 0.0000 0.0000
( 50.00%) 0.7071* C 3 s( 0.00%)p 1.00( 99.96%)d 0.00( 0.04%)
0.0000 0.0000 0.0000 0.0000 0.0005
0.0000 -0.0005 0.0000 0.9997 -0.0133
0.0000 -0.0156 -0.0117 0.0000 0.0000
7. (1.98306) BD ( 1) C 2 - H 8
( 62.04%) 0.7877* C 2 s( 29.57%)p 2.38( 70.39%)d 0.00( 0.04%)
-0.0003 0.5436 0.0126 -0.0010 -0.4980
0.0087 0.6750 -0.0118 0.0006 0.0000
-0.0159 0.0000 0.0000 -0.0049 -0.0105
( 37.96%) 0.6161* H 8 s( 99.95%)p 0.00( 0.05%)
0.9997 0.0014 0.0135 -0.0183 0.0000
8. (1.98098) BD ( 1) C 3 - C 4
( 50.00%) 0.7071* C 3 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 0.4937
0.0353 -0.6345 0.0057 -0.0006 0.0000
-0.0153 0.0000 0.0000 -0.0063 -0.0109
( 50.00%) 0.7071* C 4 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 -0.4606
0.0158 0.6590 0.0320 0.0006 0.0000
-0.0162 0.0000 0.0000 -0.0034 -0.0109
9. (1.98306) BD ( 1) C 3 - H 9
( 62.04%) 0.7876* C 3 s( 29.57%)p 2.38( 70.39%)d 0.00( 0.04%)
-0.0003 0.5436 0.0126 -0.0010 0.3356
-0.0059 0.7688 -0.0134 0.0003 0.0000
0.0122 0.0000 0.0000 -0.0113 -0.0105
( 37.96%) 0.6161* H 9 s( 99.95%)p 0.00( 0.05%)
0.9997 0.0014 -0.0091 -0.0209 0.0000
10. (1.98098) BD ( 1) C 4 - C 5
( 50.00%) 0.7071* C 4 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 -0.3027
0.0225 -0.7448 -0.0277 -0.0003 0.0000
0.0131 0.0000 0.0000 -0.0101 -0.0109
( 50.00%) 0.7071* C 5 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 0.3404
0.0356 0.7283 0.0023 0.0002 0.0000
0.0111 0.0000 0.0000 -0.0123 -0.0109
11. (1.66518) BD ( 2) C 4 - C 5
( 50.00%) 0.7071* C 4 s( 0.00%)p 1.00( 99.96%)d 0.00( 0.04%)
0.0000 0.0000 0.0000 0.0000 0.0005
0.0000 -0.0006 0.0000 0.9997 -0.0133
0.0000 -0.0158 -0.0114 0.0000 0.0000
( 50.00%) 0.7071* C 5 s( 0.00%)p 1.00( 99.96%)d 0.00( 0.04%)
0.0000 0.0000 0.0000 0.0000 0.0005
0.0000 -0.0005 0.0000 0.9997 -0.0133
0.0000 -0.0023 0.0194 0.0000 0.0000
12. (1.98306) BD ( 1) C 4 - H 10
( 62.04%) 0.7877* C 4 s( 29.57%)p 2.38( 70.39%)d 0.00( 0.04%)
-0.0003 0.5437 0.0126 -0.0010 0.8336
-0.0145 0.0938 -0.0016 -0.0003 0.0000
0.0037 0.0000 0.0000 0.0162 -0.0105
( 37.96%) 0.6161* H 10 s( 99.95%)p 0.00( 0.05%)
0.9997 0.0014 -0.0226 -0.0025 0.0000
13. (1.98098) BD ( 1) C 5 - C 6
( 50.00%) 0.7071* C 5 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 -0.7964
-0.0127 -0.1103 -0.0334 0.0003 0.0000
0.0022 0.0000 0.0000 0.0164 -0.0109
( 50.00%) 0.7071* C 6 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 0.8010
0.0198 0.0694 -0.0297 -0.0003 0.0000
0.0052 0.0000 0.0000 0.0158 -0.0109
14. (1.98306) BD ( 1) C 5 - H 11
( 62.04%) 0.7877* C 5 s( 29.57%)p 2.38( 70.39%)d 0.00( 0.04%)
0.0003 -0.5436 -0.0126 0.0010 -0.4980
0.0087 0.6751 -0.0118 0.0006 0.0000
0.0159 0.0000 0.0000 0.0049 0.0105
( 37.96%) 0.6161* H 11 s( 99.95%)p 0.00( 0.05%)
-0.9997 -0.0014 0.0135 -0.0183 0.0000
15. (1.98306) BD ( 1) C 6 - H 12
( 62.04%) 0.7876* C 6 s( 29.57%)p 2.38( 70.39%)d 0.00( 0.04%)
0.0003 -0.5436 -0.0126 0.0010 0.3356
-0.0058 0.7688 -0.0134 0.0003 0.0000
-0.0122 0.0000 0.0000 0.0113 0.0105
( 37.96%) 0.6161* H 12 s( 99.95%)p 0.00( 0.05%)
-0.9997 -0.0014 -0.0091 -0.0209 0.0000
The table above shows the bonding electrons within the molecule, it confirms the high symmetry of the benzene molecule as there are 3 distinct bonds within the molecule: C-H, sigma component C-C, and pi component C-C. The bonds between two carbon centres are sp2 (ca. 35% s 65% p) with equal contribution from each carbon towards the bond. The bond between the sp2 carbon (ca. 30% s 70% p) and the hydrogen (100% p), the contribution from the carbon is 62% and 38% from the hydrogen.
Molecular Orbital Diagram for Benzene
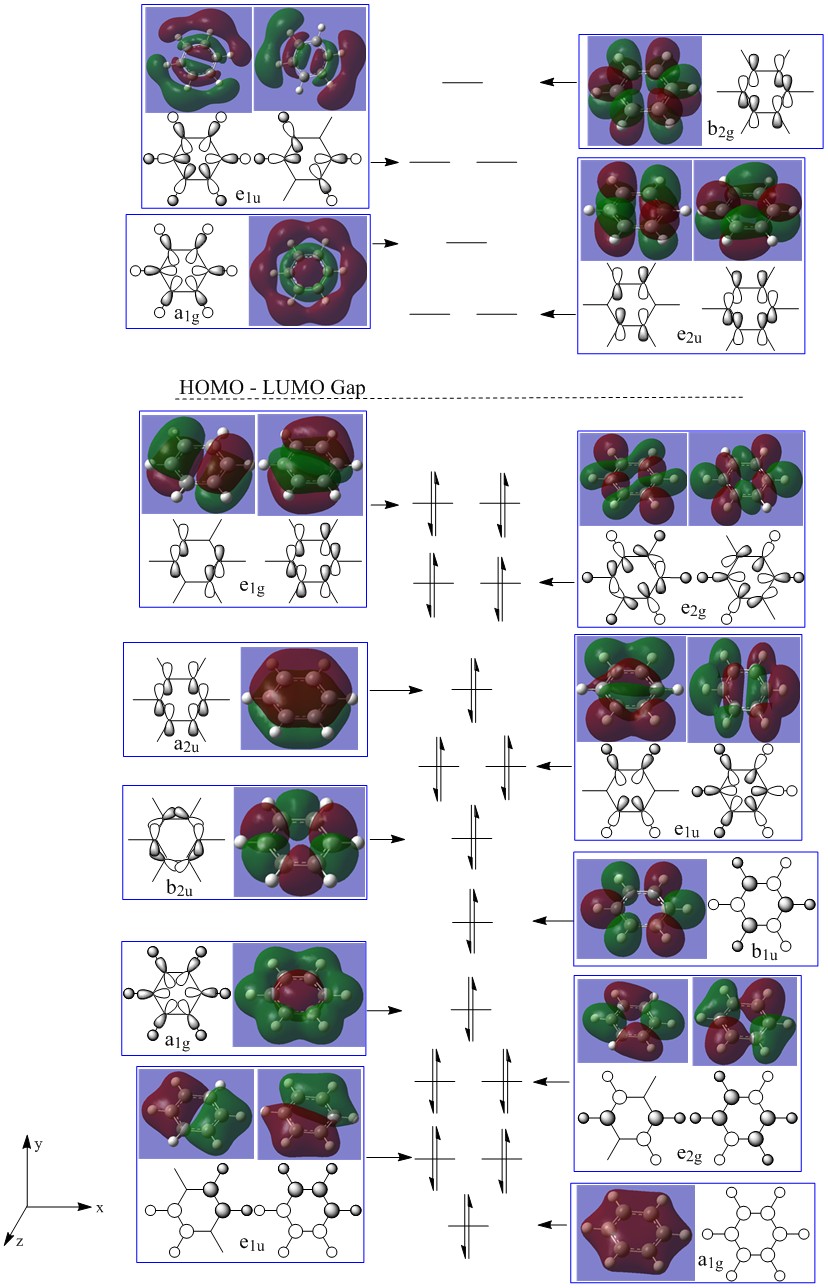
The calculated molecular orbital surfaces allow the LCAOs to be constructed. The major differences between these calculated MOs and the LCAOs are the localisation. The MOs allow the aromatic nature of the molecule to be visualised through the extensive delocalisation. This is particularly true for the all bonding pi orbital where the electron density is spread along the whole face of the cyclic ring.
Interestingly, it is shown in this molecular orbital diagram that the highest occupied sigma molecular orbital has greater antibonding character than the most bonding pi molecular orbital. This strongly suggests that excitation to cause sigma-pi transitions in benzene may occur at reasonably low energy.
The first major consideration of the nature of aromaticity in the benzene molecule was from Kekule in 1877, who thought of it as being made up of alternating single and double bonds between carbon atoms[11]. This theory was far ahead of its time and although not completely correct, still deserves high merit.
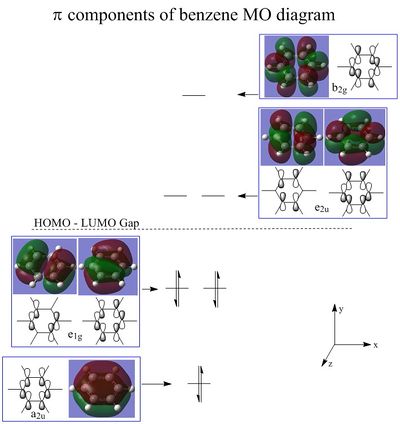
The modern day theory of aromaticity is based on a theory proposed by Huckel, stating a planar molecule with a delocalised system of electrons will have aromatic properties if the number of delocalised electron follows the 4n + 2 rule [12] where n is an integer. This directly relates to the benzene molecular orbital diagram above through consideration of the 6 pi orbitals.
The PI molecular orbitals are displayed in figure 18, there are three filled bonding orbitals containing 6 electrons - hence following 4n + 2 where n = 1. The three antibonding molecular orbitals are all unoccupied, this has a high contribution to the great stability of the benzene molecule - as filled antibonding orbitals destabilise the molecule and weaken bonds.
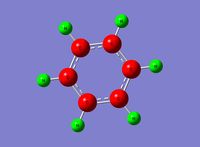
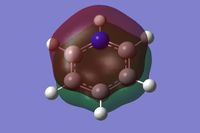
Boratabenzene Analysis
Optimisation

A molecule of boratabenzene was optimised using the method: B3LYP, and basis set: 6-31G(d,p). Keywords: opt=tight nosymm geom=connectivity int=ultrafine scf=conver=9.
| Parameter | Data |
|---|---|
| File Type | |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -219.0205229 |
| Gradient (a.u.) | 0.00000484 |
| Dipole Moment (D) | 3.92 |
| Point Group | C1 |
| Calculation Time (s) | 406.7 |
Item Value Threshold Converged? Maximum Force 0.000010 0.000015 YES RMS Force 0.000002 0.000010 YES Maximum Displacement 0.000039 0.000060 YES RMS Displacement 0.000011 0.000040 YES Predicted change in Energy=-6.013665D-10 Optimization completed. -- Stationary point found.
Figure 19 shows the bond lengths calculated for the optimised structure, the presence of the boron atom reduces the molecular symmetry which causes a change in the bond lengths of each carbon bond. The calculated values for boratabenzene are very close to literature values, where the C-C bond lengths are in the range: 1.38-1.41 A, and the B-C bond length of: 1.45 and 1.48 A[13].
Frequency Analysis
Frequency analysis was then done to confirm the optimised, low energy geometry.
| Parameter | Data |
|---|---|
| File Type | |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -219.0205229 |
| Gradient (a.u.) | 0.00000491 |
| Dipole Moment (D) | 3.92 |
| Point Group | C1 |
| Calculation Time (s) | 628.7 |
Item Value Threshold Converged? Maximum Force 0.000021 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000047 0.001800 YES RMS Displacement 0.000017 0.001200 YES Predicted change in Energy=-8.253583D-10 Optimization completed. -- Stationary point found.
Low frequencies --- -5.6580 -3.7890 -0.0013 -0.0009 -0.0008 4.2197 Low frequencies --- 371.2022 404.4383 565.0899
The low frequencies shown above are within plus/minus 6, this shows the method and basis set suit the molecular calculation. There are no negative frequencies, hence the optimised geometry is a minimum.
Population Analysis
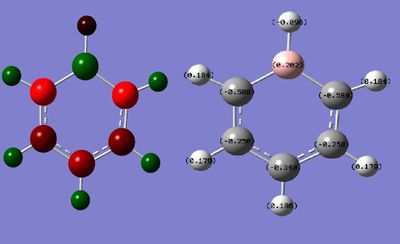
Population analysis was done using the keyword "pop=full" to give the full molecular orbitals for the molecule. The charge distribution was found to have a range: - 0.588 - + 0.588. The boron atom has a strong positive charge due to its low electronegativity compared to the surrounding carbon framework, this means the carbons adjacent have a more negative charge than for benzene, which is not evenly spread throughout. The charges together add up to - 1 as the molecule is negatively charged.
| Parameter | Data |
|---|---|
| File Type | |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -219.0205306 |
| Gradient (a.u.) | |
| Dipole Moment (D) | 2.85 |
| Point Group | C1 |
| Calculation Time (s) | 38.4 |
This calculation allows us to consider the nature of the chemical bonds within this molecule. The table below shows the atoms making up this molecule, as well as their respective tabulated charge, and the electronic distribution for each atom.
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
C 1 -0.58803 1.99901 4.57724 0.01178 6.58803
C 2 -0.25033 1.99910 4.23710 0.01413 6.25033
C 3 -0.34002 1.99907 4.32711 0.01384 6.34002
C 4 -0.25032 1.99910 4.23709 0.01413 6.25032
C 5 -0.58805 1.99901 4.57725 0.01178 6.58805
H 6 -0.09649 0.00000 1.09595 0.00054 1.09649
H 7 0.18385 0.00000 0.81397 0.00218 0.81615
H 8 0.17899 0.00000 0.81839 0.00263 0.82101
H 9 0.18574 0.00000 0.81227 0.00199 0.81426
H 10 0.17899 0.00000 0.81839 0.00263 0.82101
H 11 0.18385 0.00000 0.81397 0.00218 0.81615
B 12 0.20182 1.99906 2.78752 0.01160 4.79818
=======================================================================
* Total * -1.00000 11.99436 29.91623 0.08941 42.00000
The table below shows the characteristics of the bonding electrons within the molecule.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98271) BD ( 1) C 1 - C 2
( 49.23%) 0.7017* C 1 s( 32.50%)p 2.08( 67.45%)d 0.00( 0.05%)
0.0000 0.5698 -0.0200 0.0010 -0.0028
0.0270 0.8201 0.0353 0.0000 0.0000 The C-C bonds have almost equal contribution
0.0006 0.0000 0.0000 -0.0173 -0.0123 and sp2 hybrid orbitals as expected
( 50.77%) 0.7125* C 2 s( 37.60%)p 1.66( 62.37%)d 0.00( 0.03%)
-0.0001 0.6131 -0.0079 0.0007 0.0575
0.0311 -0.7869 -0.0164 0.0000 0.0000
-0.0020 0.0000 0.0000 -0.0150 -0.0098
2. (1.76874) BD ( 2) C 1 - C 2
( 51.88%) 0.7202* C 1 s( 0.00%)p 1.00( 99.97%)d 0.00( 0.03%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9998 -0.0054
0.0000 -0.0016 0.0185 0.0000 0.0000
( 48.12%) 0.6937* C 2 s( 0.00%)p 1.00( 99.97%)d 0.00( 0.03%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9996 -0.0213
0.0000 -0.0031 -0.0171 0.0000 0.0000
3. (1.98421) BD ( 1) C 1 - H 7
( 59.41%) 0.7708* C 1 s( 25.40%)p 2.93( 74.55%)d 0.00( 0.05%)
0.0003 -0.5040 0.0051 0.0025 -0.7905
0.0002 0.3471 0.0088 0.0000 0.0000
0.0111 0.0000 0.0000 -0.0149 0.0119
( 40.59%) 0.6371* H 7 s( 99.95%)p 0.00( 0.05%)
-0.9998 -0.0005 0.0191 -0.0100 0.0000
4. (1.96998) BD ( 1) C 1 - B 12
( 66.70%) 0.8167* C 1 s( 42.00%)p 1.38( 57.99%)d 0.00( 0.01%)
0.0000 -0.6479 -0.0159 -0.0012 0.6118 The B-C sigma type bond has much greater
-0.0293 0.4524 0.0090 0.0000 0.0000 contribution from the C compared to B
-0.0059 0.0000 0.0000 -0.0041 0.0057 The C centre is between sp2 and sp hybridised
( 33.30%) 0.5771* B 12 s( 33.40%)p 1.99( 66.53%)d 0.00( 0.08%) due to distortions from electropositive
0.0000 -0.5779 0.0059 -0.0048 -0.7056 sp3 hybridised B
-0.0393 -0.4070 0.0096 0.0000 0.0000
-0.0230 0.0000 0.0000 -0.0082 0.0133
5. (1.97969) BD ( 1) C 2 - C 3
( 49.96%) 0.7068* C 2 s( 35.53%)p 1.81( 64.43%)d 0.00( 0.04%)
-0.0001 0.5960 -0.0075 0.0006 -0.6872
-0.0034 0.4135 0.0325 0.0000 0.0000
-0.0146 0.0000 0.0000 0.0080 -0.0107
( 50.04%) 0.7074* C 3 s( 35.87%)p 1.79( 64.10%)d 0.00( 0.04%)
-0.0001 0.5989 -0.0072 0.0010 0.7062
0.0327 -0.3754 0.0141 0.0000 0.0000
-0.0137 0.0000 0.0000 0.0078 -0.0107
6. (1.98568) BD ( 1) C 2 - H 8
( 59.32%) 0.7702* C 2 s( 26.85%)p 2.72( 73.10%)d 0.00( 0.05%)
-0.0003 0.5180 0.0134 -0.0012 0.7230
-0.0089 0.4561 -0.0100 0.0000 0.0000
0.0177 0.0000 0.0000 0.0070 -0.0111
( 40.68%) 0.6378* H 8 s( 99.95%)p 0.00( 0.05%)
0.9998 0.0026 -0.0187 -0.0116 0.0000
7. (1.97969) BD ( 1) C 3 - C 4
( 50.04%) 0.7074* C 3 s( 35.87%)p 1.79( 64.10%)d 0.00( 0.04%)
-0.0001 0.5989 -0.0072 0.0010 -0.7062
-0.0327 -0.3754 0.0141 0.0000 0.0000
0.0137 0.0000 0.0000 0.0078 -0.0107
( 49.96%) 0.7068* C 4 s( 35.53%)p 1.81( 64.43%)d 0.00( 0.04%)
-0.0001 0.5960 -0.0075 0.0006 0.6872
0.0034 0.4135 0.0325 0.0000 0.0000
0.0146 0.0000 0.0000 0.0080 -0.0107
8. (1.98505) BD ( 1) C 3 - H 9
( 59.44%) 0.7710* C 3 s( 28.24%)p 2.54( 71.72%)d 0.00( 0.04%)
-0.0004 0.5312 0.0116 -0.0020 0.0000
0.0000 0.8468 -0.0076 0.0000 0.0000
0.0000 0.0000 0.0000 -0.0178 -0.0110
( 40.56%) 0.6369* H 9 s( 99.95%)p 0.00( 0.05%)
0.9998 0.0011 0.0000 -0.0217 0.0000
9. (1.98271) BD ( 1) C 4 - C 5
( 50.77%) 0.7125* C 4 s( 37.60%)p 1.66( 62.37%)d 0.00( 0.03%)
-0.0001 0.6131 -0.0079 0.0007 -0.0575
-0.0311 -0.7869 -0.0164 0.0000 0.0000
0.0020 0.0000 0.0000 -0.0150 -0.0098
( 49.23%) 0.7017* C 5 s( 32.50%)p 2.08( 67.45%)d 0.00( 0.05%)
0.0000 0.5698 -0.0200 0.0010 0.0028
-0.0270 0.8201 0.0353 0.0000 0.0000
-0.0006 0.0000 0.0000 -0.0173 -0.0123
10. (1.76873) BD ( 2) C 4 - C 5
( 48.12%) 0.6937* C 4 s( 0.00%)p 1.00( 99.97%)d 0.00( 0.03%)
0.0000 0.0000 0.0000 0.0000 0.0000slightly more uneven in contribution from C
0.0000 0.0000 0.0000 0.9996 -0.0213higher charged C contributes more towards bond
0.0000 0.0031 -0.0171 0.0000 0.0000
( 51.88%) 0.7202* C 5 s( 0.00%)p 1.00( 99.97%)d 0.00( 0.03%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9998 -0.0054
0.0000 0.0016 0.0185 0.0000 0.0000
11. (1.98568) BD ( 1) C 4 - H 10
( 59.32%) 0.7702* C 4 s( 26.85%)p 2.72( 73.10%)d 0.00( 0.05%)
0.0003 -0.5180 -0.0134 0.0012 0.7230
-0.0089 -0.4562 0.0100 0.0000 0.0000
0.0177 0.0000 0.0000 -0.0070 0.0111
( 40.68%) 0.6378* H 10 s( 99.95%)p 0.00( 0.05%)
-0.9998 -0.0026 -0.0187 0.0116 0.0000
12. (1.98421) BD ( 1) C 5 - H 11
( 59.41%) 0.7708* C 5 s( 25.40%)p 2.93( 74.55%)d 0.00( 0.05%)
0.0003 -0.5040 0.0051 0.0025 0.7906
-0.0002 0.3470 0.0088 0.0000 0.0000
-0.0111 0.0000 0.0000 -0.0149 0.0119
( 40.59%) 0.6371* H 11 s( 99.95%)p 0.00( 0.05%)
-0.9998 -0.0005 -0.0191 -0.0100 0.0000
13. (1.96998) BD ( 1) C 5 - B 12
( 66.70%) 0.8167* C 5 s( 42.00%)p 1.38( 57.99%)d 0.00( 0.01%)
0.0000 0.6479 0.0159 0.0012 0.6117
-0.0293 -0.4525 -0.0090 0.0000 0.0000
-0.0059 0.0000 0.0000 0.0041 -0.0057
( 33.30%) 0.5771* B 12 s( 33.40%)p 1.99( 66.52%)d 0.00( 0.08%)
0.0000 0.5779 -0.0059 0.0048 -0.7056
-0.0393 0.4071 -0.0096 0.0000 0.0000
-0.0230 0.0000 0.0000 0.0082 -0.0133
14. (1.98608) BD ( 1) H 6 - B 12
( 55.09%) 0.7422* H 6 s( 99.97%)p 0.00( 0.03%)
0.9998 0.0001 0.0000 0.0180 0.0000
( 44.91%) 0.6702* B 12 s( 33.17%)p 2.01( 66.78%)d 0.00( 0.06%)
-0.0005 0.5758 0.0069 -0.0060 0.0000
0.0000 -0.8172 0.0016 0.0000 0.0000
0.0000 0.0000 0.0000 -0.0213 -0.0105
The table above really emphasises the loss of symmetry due to the addition of a boron atom where contributions from each carbon to a C-C are not entirely equal in all cases.
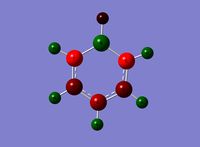
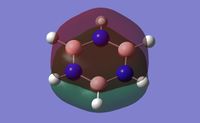
Pyridinium Analysis
Optimisation
A molecule of pyridinium was optimised using the method: B3LYP, and basis set: 6-31G(d,p). Keywords: opt=tight nosymm geom=connectivity int=ultrafine scf=conver=9.
| Parameter | Data |
|---|---|
| File Type | |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -248.6680609 |
| Gradient (a.u.) | 0.00000207 |
| Dipole Moment (D) | 27.27 |
| Point Group | C1 |
| Calculation Time (s) | 453.7 |
Item Value Threshold Converged? Maximum Force 0.000004 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000014 0.000060 YES RMS Displacement 0.000004 0.000040 YES Predicted change in Energy=-9.661140D-11 Optimization completed. -- Stationary point found.
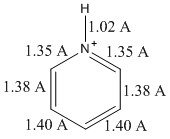
The bond lengths calculated are shown in figure 21. Although experimental literature values are not readily available for the pyridinium ion, the bond lengths can be roughly compared to pyridine molecule for ballpark figures. The N-C bond length of 1.35 A is very close to the value for pyridine, determined experimentally through use of microwave spectra, 1.3402 A, similar for the C-C bond lengths of 1.3945, and 1.3944 A respectively[14].
The dipole moment for pyridinium is significantly larger than for previously analysed molecules, this implies that the nitrogen will have a significant effect in altering the localisation of electron density.
Frequency Analysis
Frequency analysis was then done to confirm the optimised, low energy geometry.
| Parameter | Data |
|---|---|
| File Type | |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -248.6680609 |
| Gradient (a.u.) | 0.00000212 |
| Dipole Moment (D) | 27.27 |
| Point Group | C1 |
| Calculation Time (s) | 591.2 |
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000002 0.000300 YES Maximum Displacement 0.000010 0.001800 YES RMS Displacement 0.000004 0.001200 YES Predicted change in Energy=-1.046513D-10 Optimization completed. -- Stationary point found.
Low frequencies --- -9.3879 -2.9925 -0.0010 -0.0005 -0.0004 0.9537 Low frequencies --- 391.9003 404.3424 620.1996
The low frequencies are all close to zero (plus/minus 10 cm-1) and the real frequencies are all positive. This confirms the optimised structure is a minimum energy.
Population Analysis
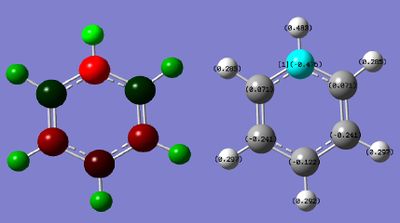
Population analysis was done using the keyword "pop=full" to give the full molecular orbitals for the molecule. The charge distribution is shown in figure 22 where the charge range is: -0.483 - +0.483. The highly electronegative nitrogen atom has substantial effects on the charge distribution of the molecule, causing electron deficiency in the carbon framework and high electron density on the nitrogen atom. The charges together add up to + 1, as the molecule is charged.
| Parameter | Data |
|---|---|
| File Type | .log |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -248.6680740 |
| Gradient (a.u.) | |
| Dipole Moment (D) | 1.87 |
| Point Group | C1 |
| Calculation Time (s) | 43.5 |
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
C 1 0.07102 1.99918 3.91065 0.01916 5.92898
C 2 -0.24106 1.99912 4.22862 0.01331 6.24106
C 3 -0.12241 1.99913 4.10941 0.01386 6.12241
C 4 -0.24106 1.99912 4.22862 0.01331 6.24106
C 5 0.07102 1.99918 3.91065 0.01916 5.92898
H 6 0.28493 0.00000 0.71397 0.00110 0.71507
H 7 0.29720 0.00000 0.70177 0.00103 0.70280
H 8 0.29169 0.00000 0.70718 0.00113 0.70831
H 9 0.29720 0.00000 0.70177 0.00103 0.70280
H 10 0.28493 0.00000 0.71397 0.00110 0.71507
H 11 0.48278 0.00000 0.51476 0.00246 0.51722
N 12 -0.47623 1.99937 5.46757 0.00929 7.47623
=======================================================================
* Total * 1.00000 11.99510 29.90895 0.09595 42.00000
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98297) BD ( 1) C 1 - C 2
( 50.42%) 0.7100* C 1 s( 38.50%)p 1.60( 61.46%)d 0.00( 0.04%)
-0.0001 0.6204 -0.0024 0.0030 0.7831 The bonding here is 50:50 contribution from
0.0046 -0.0141 -0.0331 0.0000 0.0000 each C, where both atoms are sp2 hybridised
0.0053 0.0000 0.0000 0.0168 -0.0095 to the same extent.
( 49.58%) 0.7042* C 2 s( 33.48%)p 1.99( 66.48%)d 0.00( 0.05%)
0.0000 0.5785 -0.0119 -0.0002 -0.8145
-0.0194 0.0007 -0.0320 0.0000 0.0000
-0.0047 0.0000 0.0000 0.0179 -0.0119
2. (1.98154) BD ( 1) C 1 - H 6
( 64.26%) 0.8016* C 1 s( 33.44%)p 1.99( 66.52%)d 0.00( 0.04%)
0.0004 -0.5780 -0.0180 0.0017 0.4694
-0.0193 0.6665 -0.0183 0.0000 0.0000
-0.0164 0.0000 0.0000 0.0019 0.0092
( 35.74%) 0.5978* H 6 s( 99.94%)p 0.00( 0.06%)
-0.9997 -0.0018 -0.0128 -0.0209 0.0000
3. (1.98862) BD ( 1) C 1 - N 12
( 36.68%) 0.6057* C 1 s( 28.13%)p 2.55( 71.74%)d 0.00( 0.13%) The carbon of the C-N bond is close to sp3
-0.0001 0.5293 -0.0334 -0.0013 -0.4043 hybridised - surprising as for this molecule
-0.0563 0.7417 0.0277 0.0000 0.0000 it would be expected to be sp2, however the
-0.0252 0.0000 0.0000 -0.0185 -0.0179 high electronegativity of nitrogen results
( 63.32%) 0.7957* N 12 s( 36.56%)p 1.73( 63.41%)d 0.00( 0.03%) in strongly uneven bond contributions which
-0.0001 0.6046 -0.0037 0.0006 0.3659 results in this slight change
-0.0187 -0.7069 -0.0132 0.0000 0.0000
-0.0107 0.0000 0.0000 -0.0059 -0.0115
4. (1.82446) BD ( 2) C 1 - N 12
( 28.54%) 0.5343* C 1 s( 0.00%)p 1.00( 99.83%)d 0.00( 0.17%)
0.0000 0.0000 0.0000 0.0000 0.0000 This reflects the double bond component
0.0000 0.0000 0.0000 0.9991 0.0132 for the C-N bond - where the overlap is 100%
0.0000 -0.0102 0.0394 0.0000 0.0000 p orbitals
( 71.46%) 0.8453* N 12 s( 0.00%)p 1.00( 99.98%)d 0.00( 0.02%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9999 0.0036
0.0000 0.0128 -0.0077 0.0000 0.0000
5. (1.98249) BD ( 1) C 2 - C 3
( 50.26%) 0.7089* C 2 s( 34.72%)p 1.88( 65.23%)d 0.00( 0.04%)
0.0000 0.5892 -0.0066 0.0009 0.4184
0.0371 0.6898 -0.0068 0.0000 0.0000
0.0122 0.0000 0.0000 -0.0118 -0.0115
( 49.74%) 0.7053* C 3 s( 34.45%)p 1.90( 65.51%)d 0.00( 0.04%)
0.0000 0.5869 -0.0086 0.0005 -0.3934
0.0234 -0.7063 -0.0290 0.0000 0.0000
0.0169 0.0000 0.0000 -0.0060 -0.0113
6. (1.54876) BD ( 2) C 2 - C 3
( 54.27%) 0.7367* C 2 s( 0.00%)p 1.00( 99.94%)d 0.00( 0.06%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9997 -0.0080
0.0000 -0.0086 0.0228 0.0000 0.0000
( 45.73%) 0.6762* C 3 s( 0.00%)p 1.00( 99.93%)d 0.00( 0.07%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9997 -0.0036
0.0000 -0.0241 -0.0101 0.0000 0.0000
7. (1.97822) BD ( 1) C 2 - H 7
( 64.83%) 0.8052* C 2 s( 31.78%)p 2.15( 68.19%)d 0.00( 0.03%)
0.0003 -0.5636 -0.0138 0.0005 -0.3990
0.0072 0.7227 -0.0181 0.0000 0.0000
0.0110 0.0000 0.0000 0.0085 0.0099
( 35.17%) 0.5930* H 7 s( 99.94%)p 0.00( 0.06%)
-0.9997 -0.0016 0.0116 -0.0208 0.0000
8. (1.98249) BD ( 1) C 3 - C 4
( 49.74%) 0.7053* C 3 s( 34.45%)p 1.90( 65.51%)d 0.00( 0.04%)
0.0000 0.5869 -0.0086 0.0005 -0.3935
0.0234 0.7063 0.0290 0.0000 0.0000
-0.0169 0.0000 0.0000 -0.0060 -0.0113
( 50.26%) 0.7089* C 4 s( 34.72%)p 1.88( 65.23%)d 0.00( 0.04%)
0.0000 0.5892 -0.0066 0.0009 0.4184
0.0371 -0.6898 0.0068 0.0000 0.0000
-0.0122 0.0000 0.0000 -0.0118 -0.0115
9. (1.98140) BD ( 1) C 3 - H 8
( 64.64%) 0.8040* C 3 s( 31.07%)p 2.22( 68.90%)d 0.00( 0.03%)
-0.0003 0.5572 0.0131 -0.0007 0.8298
-0.0199 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0153 -0.0101
( 35.36%) 0.5947* H 8 s( 99.94%)p 0.00( 0.06%)
0.9997 0.0018 -0.0242 0.0000 0.0000
10. (1.98297) BD ( 1) C 4 - C 5
( 49.58%) 0.7042* C 4 s( 33.48%)p 1.99( 66.48%)d 0.00( 0.05%)
0.0000 0.5785 -0.0119 -0.0002 -0.8145
-0.0194 -0.0007 0.0320 0.0000 0.0000
0.0047 0.0000 0.0000 0.0179 -0.0119
( 50.42%) 0.7100* C 5 s( 38.50%)p 1.60( 61.46%)d 0.00( 0.04%)
-0.0001 0.6204 -0.0024 0.0030 0.7831
0.0046 0.0141 0.0331 0.0000 0.0000
-0.0053 0.0000 0.0000 0.0168 -0.0095
11. (1.61443) BD ( 2) C 4 - C 5
( 52.23%) 0.7227* C 4 s( 0.00%)p 1.00( 99.94%)d 0.00( 0.06%)
0.0000 0.0000 0.0000 0.0000 0.0000 C-C bond has uneven contribution from each C
0.0000 0.0000 0.0000 0.9997 -0.0068 due to the difference in charge of each atom
0.0000 -0.0191 -0.0159 0.0000 0.0000
( 47.77%) 0.6912* C 5 s( 0.00%)p 1.00( 99.94%)d 0.00( 0.06%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9995 -0.0175
0.0000 0.0196 -0.0153 0.0000 0.0000
12. (1.97822) BD ( 1) C 4 - H 9
( 64.83%) 0.8052* C 4 s( 31.78%)p 2.15( 68.19%)d 0.00( 0.03%)
-0.0003 0.5636 0.0138 -0.0005 0.3989
-0.0072 0.7228 -0.0181 0.0000 0.0000
0.0110 0.0000 0.0000 -0.0085 -0.0099
( 35.17%) 0.5930* H 9 s( 99.94%)p 0.00( 0.06%)
0.9997 0.0016 -0.0116 -0.0208 0.0000
13. (1.98154) BD ( 1) C 5 - H 10
( 64.26%) 0.8016* C 5 s( 33.44%)p 1.99( 66.52%)d 0.00( 0.04%)
-0.0004 0.5780 0.0180 -0.0017 -0.4694
0.0193 0.6665 -0.0183 0.0000 0.0000
-0.0164 0.0000 0.0000 -0.0019 -0.0092
( 35.74%) 0.5978* H 10 s( 99.94%)p 0.00( 0.06%)
0.9997 0.0018 0.0128 -0.0209 0.0000
14. (1.98862) BD ( 1) C 5 - N 12
( 36.68%) 0.6057* C 5 s( 28.13%)p 2.55( 71.74%)d 0.00( 0.13%)
-0.0001 0.5293 -0.0334 -0.0013 -0.4042
-0.0563 -0.7417 -0.0277 0.0000 0.0000
0.0252 0.0000 0.0000 -0.0185 -0.0179
( 63.32%) 0.7957* N 12 s( 36.56%)p 1.73( 63.41%)d 0.00( 0.03%)
-0.0001 0.6046 -0.0037 0.0006 0.3659
-0.0187 0.7069 0.0132 0.0000 0.0000
0.0107 0.0000 0.0000 -0.0059 -0.0115
15. (1.98630) BD ( 1) H 11 - N 12
( 25.41%) 0.5041* H 11 s( 99.88%)p 0.00( 0.12%)
-0.9994 0.0064 -0.0342 0.0000 0.0000
( 74.59%) 0.8637* N 12 s( 26.82%)p 2.73( 73.15%)d 0.00( 0.02%)
0.0002 -0.5178 -0.0066 0.0013 0.8553
-0.0091 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 -0.0115 0.0106
There are a number of slight differences in the bond contributions as well as hybridisation between the carbon bonds tabulated above, this is the result of the highly electronegative nitrogen atom pulling electron density from the carbon chain. This causes uneven electron density across different carbons depending on their proximity to the nitrogen.
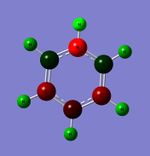
Borazine Analysis
Borazine is known essentially as the inorganic version of benzene, it is isoelectronic, and an aromatic molecule with 6 pi electrons. It has fairly substantial differences from benzene however due to the polarity of B-N, this causes a decrease in the cyclic delocalisation of the pi system[15]. Whether or not this molecule is actually aromatic has been a controversial topic for a number of years, through considering magnetic properties and ring currents the aromatic nature of the molecule is questionable. However through a number of recent computational analyses, the aromaticity is confirmed[16]. Though it is agreed that the extent of aromaticity for borazine is significantly lower than for benzene.
Optimisation
A molecule of borazene was optimised using the method: B3LYP, and basis set: 6-31G(d,p). Keywords: opt=tight nosymm geom=connectivity int=ultrafine scf=conver=9.
| Parameter | Data |
|---|---|
| File Type | |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -242.6845999 |
| Gradient (a.u.) | 0.00000066 |
| Dipole Moment (D) | 0.00 |
| Point Group | C1 |
| Calculation Time (s) | 1374.1 |
Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000014 0.000060 YES RMS Displacement 0.000004 0.000040 YES Predicted change in Energy=-2.772566D-11 Optimization completed. -- Stationary point found.
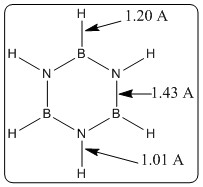
The bond lengths for optimised borazine are shown in figure 23 above. The bond lengths calculated average at 1.43 A, all bond lengths are the same throughout the molecule, another similarity to benzene. This compares very well to the literature values: average B-N length of 1.429 A, measured by single-crystal X-ray crystallography[17]. The bond angles are also exactly confirmed by the literature, B-N-B angle: 122.9 degrees (literature: 122.9 degrees), N-B-N angle: 117.1 degrees (literature: 117.1 degrees). This shows how accurate this method and basis set assumptions are for borazine - as provide highly accurate figures all round.
Frequency Analysis
Frequency analysis was then done to confirm the minimum energy geometry calculated above.
| Parameter | Data |
|---|---|
| File Type | |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -242.6845999 |
| Gradient (a.u.) | 0.00000069 |
| Dipole Moment (D) | 0.00 |
| Point Group | C1 |
| Calculation Time (s) | 629.9 |
Item Value Threshold Converged? Maximum Force 0.000002 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000015 0.001800 YES RMS Displacement 0.000007 0.001200 YES Predicted change in Energy=-3.293100D-11 Optimization completed. -- Stationary point found.
Low frequencies --- -6.3626 0.0007 0.0008 0.0008 3.6392 8.0904 Low frequencies --- 289.6210 289.6335 404.4599
The low frequencies are very close to zero (plus/minus 8) and all real frequencies are positive values, showing that the minimum energy geometry has been found.
Population Analysis
Population analysis was done using the keyword "pop=full" to give the full molecular orbitals for the molecule. The charge distribution for the molecule was calculated and shown in figure 24. This corresponds to the charge range: - 1.102 - + 1.102. This is the highest range of the four aromatic molecules as a result of the strong polarity of the bonds within the molecule. The boron is electropositive and the nitrogen strongly electronegative, this combined with the alternating sequence of atoms causes high differences in the charge of each atom. The nitrogen atom is strongly negative, and the boron atoms are strongly positive. The sum of the charges gives a charge of 0, due to the molecule having an overall neutral charge.
| Parameter | Data |
|---|---|
| File Type | |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy (a.u.) | -242.6845999 |
| Gradient (a.u.) | |
| Dipole Moment (D) | 0.00 |
| Point Group | C1 |
| Calculation Time (s) | 72.8 |
The nature of the bonds within the molecule can be further analysed using the Gaussian calculated data shown below:
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
H 1 0.43200 0.00000 0.56571 0.00228 0.56800
H 2 -0.07654 0.00000 1.07584 0.00069 1.07654
H 3 0.43201 0.00000 0.56571 0.00228 0.56799
H 4 -0.07654 0.00000 1.07584 0.00069 1.07654
H 5 0.43201 0.00000 0.56571 0.00228 0.56799
H 6 -0.07654 0.00000 1.07585 0.00069 1.07654
B 7 0.74694 1.99917 2.23868 0.01521 4.25306
B 8 0.74694 1.99917 2.23868 0.01521 4.25306
B 9 0.74694 1.99917 2.23868 0.01521 4.25306
N 10 -1.10241 1.99943 6.09820 0.00478 8.10241
N 11 -1.10240 1.99943 6.09820 0.00478 8.10240
N 12 -1.10241 1.99943 6.09820 0.00478 8.10241
=======================================================================
* Total * 0.00000 11.99579 29.93530 0.06891 42.00000
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98494) BD ( 1) H 1 - N 11
( 28.08%) 0.5299* H 1 s( 99.91%)p 0.00( 0.09%)
0.9996 -0.0010 -0.0294 0.0002 -0.0032
( 71.92%) 0.8481* N 11 s( 22.82%)p 3.38( 77.15%)d 0.00( 0.03%)
-0.0002 0.4776 -0.0114 0.0006 0.8729
0.0130 -0.0053 -0.0001 0.0962 0.0014
-0.0001 0.0036 0.0000 0.0120 -0.0116
2. (1.98670) BD ( 1) H 2 - B 9
( 54.03%) 0.7351* H 2 s( 99.96%)p 0.00( 0.04%)
0.9998 0.0002 -0.0094 0.0167 -0.0011
( 45.97%) 0.6780* B 9 s( 37.47%)p 1.67( 62.47%)d 0.00( 0.07%)
-0.0006 0.6120 0.0129 -0.0016 0.3884
-0.0132 -0.6865 0.0234 0.0434 -0.0015
-0.0202 0.0005 -0.0022 -0.0121 -0.0097
3. (1.98494) BD ( 1) H 3 - N 12
( 28.08%) 0.5299* H 3 s( 99.91%)p 0.00( 0.09%)
-0.9996 0.0010 -0.0148 -0.0255 -0.0016
( 71.92%) 0.8481* N 12 s( 22.82%)p 3.38( 77.15%)d 0.00( 0.03%)
0.0002 -0.4776 0.0114 -0.0006 0.4411
0.0066 0.7579 0.0113 0.0480 0.0007
-0.0106 -0.0016 -0.0011 0.0060 0.0118
4. (1.98670) BD ( 1) H 4 - B 7
( 54.03%) 0.7351* H 4 s( 99.96%)p 0.00( 0.04%)
0.9998 0.0002 -0.0096 -0.0166 -0.0010
( 45.97%) 0.6780* B 7 s( 37.47%)p 1.67( 62.47%)d 0.00( 0.07%)
-0.0006 0.6120 0.0129 -0.0016 0.3968
-0.0135 0.6817 -0.0232 0.0432 -0.0015
0.0205 0.0006 0.0022 -0.0116 -0.0097
5. (1.98494) BD ( 1) H 5 - N 10
( 28.08%) 0.5299* H 5 s( 99.91%)p 0.00( 0.09%)
0.9996 -0.0010 0.0145 -0.0257 0.0016
( 71.92%) 0.8481* N 10 s( 22.82%)p 3.38( 77.15%)d 0.00( 0.03%)
-0.0002 0.4776 -0.0114 0.0006 -0.4318
-0.0064 0.7632 0.0113 -0.0482 -0.0007
-0.0104 0.0016 -0.0012 -0.0063 -0.0118
6. (1.98670) BD ( 1) H 6 - B 8
( 54.03%) 0.7351* H 6 s( 99.96%)p 0.00( 0.04%)
0.9998 0.0002 0.0191 -0.0001 0.0021
( 45.97%) 0.6780* B 8 s( 37.47%)p 1.67( 62.47%)d 0.00( 0.07%)
-0.0006 0.6120 0.0129 -0.0016 -0.7851
0.0268 0.0048 -0.0002 -0.0865 0.0029
-0.0003 0.0044 0.0000 0.0234 -0.0094
7. (1.98437) BD ( 1) B 7 - N 10
( 23.53%) 0.4851* B 7 s( 31.25%)p 2.19( 68.50%)d 0.01( 0.25%)
-0.0003 0.5588 -0.0174 0.0032 -0.8205
-0.0448 -0.0174 0.0362 -0.0904 -0.0050
0.0051 0.0088 0.0006 0.0444 -0.0197
( 76.47%) 0.8745* N 10 s( 38.55%)p 1.59( 61.44%)d 0.00( 0.01%)
0.0000 0.6209 0.0043 -0.0001 0.7769
-0.0079 0.0562 0.0138 0.0856 -0.0009
0.0008 0.0024 0.0001 0.0070 -0.0083
8. (1.98437) BD ( 1) B 7 - N 11
( 23.53%) 0.4851* B 7 s( 31.25%)p 2.19( 68.50%)d 0.01( 0.25%)
-0.0003 0.5588 -0.0174 0.0032 0.3865
0.0534 -0.7283 -0.0216 0.0432 0.0059
-0.0355 0.0009 -0.0040 -0.0278 -0.0205
( 76.47%) 0.8745* N 11 s( 38.55%)p 1.59( 61.44%)d 0.00( 0.01%)
0.0000 0.6209 0.0043 -0.0001 -0.3315
0.0158 0.7091 -0.0002 -0.0371 0.0017
-0.0056 0.0011 -0.0006 -0.0045 -0.0084
9. (1.82089) BD ( 2) B 7 - N 11
( 11.79%) 0.3433* B 7 s( 0.00%)p 1.00( 99.62%)d 0.00( 0.38%)
0.0000 0.0000 0.0000 0.0000 -0.1093
0.0035 0.0008 0.0000 0.9916 -0.0313
0.0063 0.0211 -0.0571 -0.0023 0.0042
( 88.21%) 0.9392* N 11 s( 0.00%)p 1.00(100.00%)d 0.00( 0.00%)
0.0000 0.0000 0.0000 0.0000 -0.1095
0.0000 0.0008 0.0000 0.9940 -0.0003
-0.0001 -0.0045 0.0005 0.0005 -0.0009
10. (1.98437) BD ( 1) B 8 - N 10
( 23.53%) 0.4851* B 8 s( 31.25%)p 2.19( 68.50%)d 0.01( 0.25%)
0.0003 -0.5588 0.0174 -0.0032 -0.4337
0.0081 -0.7009 -0.0573 -0.0472 0.0009
-0.0416 -0.0020 -0.0045 0.0171 0.0204
( 76.47%) 0.8745* N 10 s( 38.55%)p 1.59( 61.44%)d 0.00( 0.01%)
0.0000 -0.6209 -0.0043 0.0001 0.4447
0.0077 0.6435 -0.0139 0.0485 0.0009
-0.0066 -0.0013 -0.0007 0.0027 0.0084
11. (1.82089) BD ( 2) B 8 - N 10
( 11.79%) 0.3433* B 8 s( 0.00%)p 1.00( 99.62%)d 0.00( 0.38%)
0.0000 0.0000 0.0000 0.0000 -0.1093
0.0034 0.0008 0.0000 0.9916 -0.0313
-0.0052 0.0380 0.0472 -0.0043 0.0073
( 88.21%) 0.9392* N 10 s( 0.00%)p 1.00(100.00%)d 0.00( 0.00%)
0.0000 0.0000 0.0000 0.0000 -0.1096
0.0000 0.0008 0.0000 0.9940 -0.0003
0.0005 0.0018 -0.0042 -0.0002 0.0004
12. (1.98437) BD ( 1) B 8 - N 12
( 23.53%) 0.4851* B 8 s( 31.25%)p 2.19( 68.50%)d 0.01( 0.25%)
0.0003 -0.5588 0.0174 -0.0032 -0.4251
0.0088 0.7062 0.0572 -0.0474 0.0009
0.0412 -0.0019 0.0046 0.0181 0.0204
( 76.47%) 0.8745* N 12 s( 38.55%)p 1.59( 61.44%)d 0.00( 0.01%)
0.0000 -0.6209 -0.0043 0.0001 0.4368
0.0079 -0.6488 0.0138 0.0487 0.0009
0.0066 -0.0013 0.0007 0.0029 0.0084
13. (1.98437) BD ( 1) B 9 - N 11
( 23.53%) 0.4851* B 9 s( 31.25%)p 2.19( 68.50%)d 0.01( 0.25%)
0.0003 -0.5588 0.0174 -0.0032 -0.3953
-0.0536 -0.7235 -0.0209 -0.0430 -0.0059
-0.0361 -0.0009 -0.0039 0.0269 0.0205
( 76.47%) 0.8745* N 11 s( 38.55%)p 1.59( 61.44%)d 0.00( 0.01%)
0.0000 -0.6209 -0.0043 0.0001 0.3402
-0.0158 0.7050 0.0000 0.0369 -0.0017
-0.0057 -0.0011 -0.0006 0.0044 0.0084
14. (1.98437) BD ( 1) B 9 - N 12
( 23.53%) 0.4851* B 9 s( 31.25%)p 2.19( 68.50%)d 0.01( 0.25%)
-0.0003 0.5588 -0.0174 0.0032 -0.8202
-0.0453 0.0274 -0.0357 -0.0904 -0.0050
-0.0062 0.0088 -0.0007 0.0443 -0.0197
( 76.47%) 0.8745* N 12 s( 38.55%)p 1.59( 61.44%)d 0.00( 0.01%)
0.0000 0.6209 0.0043 -0.0001 0.7762
-0.0081 -0.0657 -0.0137 0.0856 -0.0009
-0.0010 0.0024 -0.0001 0.0070 -0.0083
15. (1.82089) BD ( 2) B 9 - N 12
( 11.79%) 0.3433* B 9 s( 0.00%)p 1.00( 99.62%)d 0.00( 0.38%)
0.0000 0.0000 0.0000 0.0000 -0.1093
0.0035 0.0008 0.0000 0.9916 -0.0313
-0.0011 -0.0591 0.0099 0.0066 -0.0114
( 88.21%) 0.9392* N 12 s( 0.00%)p 1.00(100.00%)d 0.00( 0.00%)
0.0000 0.0000 0.0000 0.0000 -0.1095
0.0000 0.0008 0.0000 0.9940 -0.0003
-0.0004 0.0027 0.0037 -0.0003 0.0005
The bond analysis above confirms the symmetry of this molecule, there are four distinct types of bonds found in this molecule: B-H, N-H, B-N (sigma), B-N (pi). The high polarity of the B-N bond can be confirmed through consideration of the bond contributions, for the sigma component ca. 75 % of the bond is contributed from the nitrogen, and for the pi ca. 88 % is contributed from the nitrogen. Together this reinforces a very high bond polarity, responsible for a number of borazines properties.
Charge Comparison
As the standard for this aromaticity study, the charge distribution for benzene shows the highly symmetric nature of this molecule. Each carbon of the framework has the same charge, of - 0.239, due to the electronegativity difference between carbon and hydrogen.
Comparing benzene to the isoelectronic boratabenzene. The electropositive boron atom has a positive charge of + 0.202, attached to a slightly negatively charged hydrogen. The carbon atoms bonded to the electropositive boron are highly negatively charged due to electron density from the boron. The overall carbon framework is more electron rich and therefore negatively charged than benzene.

Pyridinium contains a highly electronegative nitrogen atom which strongly pulls electron density from the carbon framework and the attached hydrogen. The carbon atoms attached to the nitrogen are positively charged due to the nitrogen inductive effects[18], the charge distribution is as expected when considering where the positive charges are localised in the resonance forms, illustrated in figure 25.
Borazine is very different from benzene in terms of charge distribution, combination of highly electronegative nitrogen and electropositive boron atom causes high bond polarity. The nitrogen has high negative charge of - 1.102, adjacent to the highly positively charged boron atom, + 0.747. Borazine does however have similarities with benzene, particularly the high symmetry where each atom of the same element has the same charge. This is quite different to boratabenzene and pyridinium where the presence of a singular main group atom causes changes in the charges, and bond lengths across the carbon framework.
MO Comparison
The MOs chosen for this comparison show some interesting changes between the four aromatic molecules, the three MOs chosen to analyse are all pi molecular orbitals due to the nature of this study on aromaticity. MO 17 is the fully bonding pi molecular orbital, 20 and 21 are the two HOMO orbitals for benzene. Due to the loss in symmetry for pyridinium and boratabenzene MO 20 and 21 are different energies. Borazene is a highly symmetric molecule and maintains a level of degeneracy in its molecular orbitals, hence similarly to benzene these two orbitals are degenerate.
MO 17
The all bonding pi orbital has a similar form for all four molecules, and is built up of all-bonding p orbitals from each atom, hence this is the lowest energy pi orbital. Benzene has a perfectly symmetrical molecular orbital, very similar to borazine. There is a slight difference as the MO surface is slightly uneven, stretching further for the nitrogen atoms and less for the boron, this is only a small difference however. Their energies are also quite similar, particularly compared to pyridinium and boratabenzene. This is due to the highly stable nitrogen atomic orbitals to some extent "cancelling out" the destabilising boron orbitals, giving a mid point close to our standard.
Pyridinium has a much lower energy MO for the all bonding pi orbital, due to the stabilising nitrogen atomic orbitals. This also causes a slight distortion in the MO surface - with more of it localised around the nitrogen.
The opposite of this is true for boratabenzene, which, due to the less stable boron orbital, causes an increase in energy, with less of the MO localised around the boron atom.
MO 21 and 20
MO 21 and 20 are different energies for pyridinium, the lower energy MO 20 has an atomic orbital from the nitrogen atom, which lowers the energy through contribution of higher bonding electron density. MO 21 has higher energy due to less bonding electron density as the nitrogen atom does not contribute towards the molecular orbital. The energies for these orbitals is considerably lower than that of benzene. This is also due to the stabilising high bonding electron density from the nitrogen, giving the MO much higher bonding character compared to benzene.
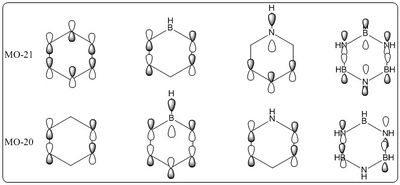
Boratabenzene has the MO containing B AO contribution higher energy than that of no B contribution. This is due to the low stability of the positively charge boron which overall destabilises the molecular orbital. The overall energy of these two molecular orbitals are much higher than benzene, due to the destabilising boron atom which causes higher antibonding character. MO 21 has a positive value for energy, this makes it overall antibonding - as electron density in this orbital overall increases the energy of the molecule. As this is a filled orbital it rationalises the higher energy, lower stability of this molecule in comparison to benzene.
MO 20 and 21 are similar forms for benzene and borazine, for benzene these orbitals are perfectly symmetric, reflecting that character of the benzene molecule. Although borazine is relatively symmetric, compared to pyridinium and boratabenzene, it is less symmetric compared to benzene (D3h point group compared to D6h). This results in slight changes in the MO forms, namely for MO 21, the MO surface has greater area around the N-B-N section compared to the opposite phase B-N-B section. This is principally due to the high electronegativity of nitrogen and the resulting negative charge which is able to contribute more electron density to the MO surface. Similarly MO 20 is slightly asymmetric due to an increase in MO surface size around the nitrogen atom.
The degenerate HOMO orbitals for borazine are more stable (lower energy) than the corresponding ones in benzene, this results in an overall higher HOMO-LUMO gap. However the overall energy spacing between the pi system is lower energy in borazine, this is thought to be due to the contributions from atomic orbitals towards the overall molecular orbital. The occupied pi MOs of borazine are largely constructed from nitrogen atomic orbitals, the unoccupied pi MOs have strong boron atomic orbital character. However since there are no two boron or nitrogen atoms next to each other there is less interaction within the pi MO set, hence less spaced MOs. For benzene the carbon atomic orbitals interact with each other, thus increasing energy different between orbitals[19].
Full MO Diagram Differences
The three main group aromatics show a number of change from the benzene molecular orbital diagram shown above. A significant difference for the MO diagrams of boratabenzene and pyridinium is the complete loss of any degeneracy in the orbitals. This is related to the low symmetry of the molecules (C2v compared to D6h for benzene) and differences in bond lengths.
Borazine is more symmetric, and maintains the degeneracy shown in the benzene MO diagram, however there is a difference in the distribution of energy levels - it doesn't exactly match benzene as the symmetry point group is lowered to D3h.
There are vast differences in the overall energy levels of each MO diagam. Borazine is very similar to benzene with all bonding orbitals being reasonably low energy, a contributing factor to the stability of the aromatic. The energy values for the MO diagram of pyridinium is much lower than that of benzene due to the stabilising nitrogen contribution. Boratabenzene has considerably greater energy MO diagram due to the destabilising boron contribution.
Analysis of Borazine
As mentioned previously, there has been a level of debate in a number of papers about whether borazine is in fact an inorganic benzene, or whether this was a hastily formed title. The aromaticity of these molecules has been extentively computed and spectroscopically studied, such as by NMR. Overall a delocalised system was confirmed, similar to our computed orbitals above. The stabilisation energy from borazine's aromatic system was calculated to be ca. 1/3 lower than for benzene[20].
The chemical reactivity differences between benzene and borazene are substantial. Borazine predominantly undergoes electrophilic addition reactions instead of electrophilic substitutions, which strongly implies the reactivity of borazine is not driven to reform pi system aromaticity. Electrophilic substitution reactions have been observed for borazine with alkylating ions such as Me2F+ and Me3C+, with the alkyl group falling on the nucleophilic nitrogen centre[21].
Some of the reasons for these differences in aromaticity relate to the polarisation of the bond, confirmed with the charge distribution analysis above for the two molecules. Due to the strong difference in charge between the boron and the nitrogen the bonds are considerably more reactive than the non-polar bonds of benzene. This explains the instability of borazine and its tendancy to decompose over time compared to the highly stable benzene.
Boratabenzene Chemistry
The derivatives of boratabenzene can be used as ligands in transition metal coordination chemistry. The complexation of this anion with a lithium cation forms a strong complex, which, due to covalent contributions to this bond, causes slight bond lengthening when compared to the singly charged anion.
The interesting factor resulting from this complexation is the ability for the lithium to migrate between the two faces of the ring, with a relatively low energy barrier[22]. Figure 27 shows this transition with the intermediate structure highlighted.
References
- ↑ Kawaguchi, K., Journal of Chemical Physics 1992, 96 (5), 3411-3415 DOI:10.1063/1.461942
- ↑ David R. Lide, ed., CRC Handbook of Chemistry and Physics, Internet Version 2005, <http://www.hbcpnetbase.com>, Pg 1399
- ↑ Martinsen, K. et al., Journal of Molecular Structure 1996, 385 (3), 159-165.DOI:10.1016/S0022-2860(96)09435-5
- ↑ Pauling, L, The nature of chemical bond, Cornell University Press, 3rd Edition, 1960, Page 93
- ↑ Pauling, L, The nature of chemical bond, Cornell University Press, 3rd Edition, 1960, Page 6
- ↑ Minkin, V, Pure Appl. Chem., 1999, Vol. 71, No. 10, pp. 1919-1981 DOI:10.1351/pac199971101919
- ↑ Atkins, P et. al., Atkins' Physical Chemistry, OUP Oxford, 9th edition, 2009, Pg 464
- ↑ Norman, N, Polyhedron, 1993, 12, 20, 2431-2446 DOI:10.1016/S0277-5387(00)83067-3
- ↑ Mo et al., J. Am. Chem. Soc. 2004, 126, 3974-3982 DOI:10.1021/ja039778l
- ↑ Trotter, J, Tetrahedron, Volume 8, Issues 1–2, 1960, Pages 13-22 DOI:101016/S0040-4020(01)933253-3
- ↑ Gero, A et al. Journal of Chemical Education, 1954, 31 (4), 201 DOI:10.1021/ed031p201
- ↑ Hepworth, J. et al., Aromatic Chemistry, RSC, 2002, pg 5-7
- ↑ Diego A. Hoic et. al., J. Am. Chem. Soc., 1995, 117 (32), pg 8480–8481 DOI:10.1021/ja00137a030
- ↑ Bak, B et al., Journal of Molecular Spectroscopy, Volume 2, Issues 1–6, 1958, Pg 361-368, DOI:10.1016/0022-2852(58)90087-0
- ↑ Boggavarapu, K et al. Inorg. Chem. 2001, 40, 3615-3618 DOI:10.1021/ic001394y
- ↑ Islas, R et. al., Structural Chemistry, 2007, Volume 18, Issue 6, pp 833-839 DOI:10.1007%2Fs11224-007-9229-z
- ↑ Boese, R et al., Chemische Berichte, Volume 127, Issue 10, pages 1887–1889, October 1994, DOI:10.1002/cber.19941271011
- ↑ Joule, J et al., Heterocyclic Chemistry, Wiley, Fifth edition, 2010, Pg 7-8
- ↑ Peyerimhoff, S et al., Theoret. chim. Acta (Berl.) 19, 1-- 19 (1970) DOI:10.1007/BF00527373
- ↑ Chiavarino, B. et al. J. Am. Chem. Soc. 1999, 121, 11204-11210 DOI:10.1021/ja992220m
- ↑ Chiavarino, B. et al. J. Am. Chem. Soc. 1999, 121, 2619.DOI:10.1021/ja983799b
- ↑ Minyaev, R et al., Russian Chemical Bulletin, December 2001, Volume 50, Issue 12, pp 2325-2335 DOI:10.1023/A:1015067025720