Rep:Mod:elle0000

1. The Molecular Mechanics Model

This module entails applying the theories and calculations derived from molecular mechanics to given molecules, using their lowest energy conformations to support real life observations and reactivity. Molecular mechanics assumes the total energy of a molecule is equivalent to the sum of five independent terms:

• Dipole-dipole interactions
• Van der Waals interactions
• Tetra-atomic bond torsion angles
• Tri-atomic bond angles
• Diatomic bond stretches

Bond lengths, bond angles and dihedral angles can be adjusted by the model in order to generate the minimal energy conformation. Molecular mechanics provides an instrument to predict and justify the optimised geometry of a molecule, the preferred reaction mechanism and the total energy of the molecule, taking into account the relative contributions from the five parameters listed above.

---

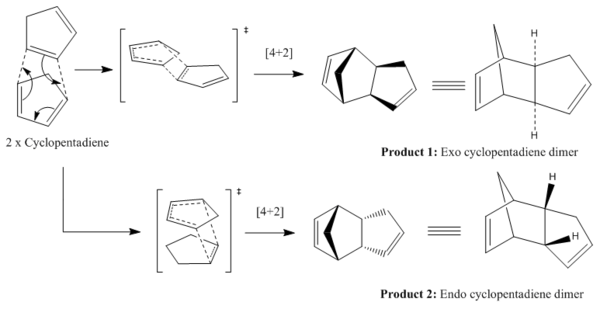
The Hydrogenation of Cyclopentadiene Dimer

Dimerisation of Cyclopentadiene

Cyclopentadiene undergoes a [π4s + π2s] Diels-Alder cycloaddition to form a cyclopentadiene dimer. This reaction will be explored through molecular mechanics to predict and verify which of the stereoisomers is produced from the dimerisation.

MM2 calculated energies for dimer products, 1 & 2

Parameter	Molecule 1	Molecule 2
Stretch	1.2833	1.2539
Bend	20.5902	20.8745
Stretch-Bend	-0.8389	-0.8375
Torsion	7.6486	9.5063
Non-1,4 VDW	-1.4184	-1.5531
1,4 VDW	4.2363	4.3071
Dipole/Dipole	0.3773	0.4475
Total Energy /kcalmol-1	31.8783	33.9987
Total Energy /kJmol-1	133.3788	142.251

The molecular mechanics model shows that the exo dimer, 1 is thermodynamically more stable, since it is 8.87 kJmol-1 lower in energy than the endo product, 2. The majority of this energy difference (86.7%) is due to the change of torsion angle. However, experimentally it is only the endo product that is formed from the dimerisation, implying that the reaction must proceed under kinetic control; thus, the endo dimer is the kinetic product. This is reasoned since the endo transition state is lower in energy, making this reaction pathway more kinetically favourable due to the greater probability of surpassing the lower activation energy. This can be justified by secondary orbital interactions between the HOMO and LUMO pz orbitals. Hence, the observed mode of dimerisation of cyclopentadiene is via an endo route, rather than the exo.

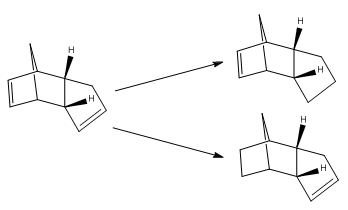
Hydogenation of Endo Cyclopentadiene Dimer

The relative ease of hydrogenation of the endo cyclopentadiene dimer (2) will now be examined using the same methods used to calculate cyclopentadiene dimerisation; i.e. Molecular mechanics (MM2 force fields)

MM2 calculated energies for hydrogenated products, 3 & 4

Parameter	Molecule 1	Molecule 2
Stretch	1.3009	1.0812
Bend	19.8983	14.4964
Stretch-Bend	-0.8376	-0.5416
Torsion	10.774	12.5079
Non-1,4 VDW	-1.1967	-1.0375
1,4 VDW	5.5885	4.5137
Dipole/Dipole	0.1621	0.1407
Total Energy /kcalmol-1	35.6895	31.1609
Total Energy /kJmol-1	149.3249	130.3772

Dihydro 4 shows the most thermodynamic hydrogenation, since it has a lower total energy than 3 by 18.95 kJmol-1, proving this product would be more easily formed. The difference between the two energies is largely to do with the bending term, which contributes 119.3% to the energy difference! This is reinforced by the fact that the norborene carbon-carbon double bond feels excess ring strain owing to the bridging methylene group. Therefore, relief of this strain (i.e. by forming 4) would be more favourable than reduction of the cyclopentene.

Energy difference between dimer 2 and respective dihydro derivatives, 3 & 4

Parameter	2→3	2→4
Stretch	-0.047	0.1727
Bend	0.9762	6.3781
Stretch-Bend	0.0001	-0.2959
Torsion	-1.2677	-3.0016
Non-1,4 VDW	-0.3564	-0.5156
1,4 VDW	-1.2814	-0.2066
Dipole/Dipole	0.2854	0.3068
Total Energy Difference /kcalmol-1	-1.6908	2.8378
Total Energy Difference /kJmol-1	-7.07434	11.87336

Formation of 3 & 4 dihydro derivatives from dimer 2

To view the hydrogenation as a reaction from 2→3 and 2→4, the total energy differences and the energies of each of the parameters have been compared. As evident, the formation of dihydro 4 is much more thermodynamically favourable since energy will be generated in forming 4, rather than consumed, as seen by the formation of dihydro 3.

---

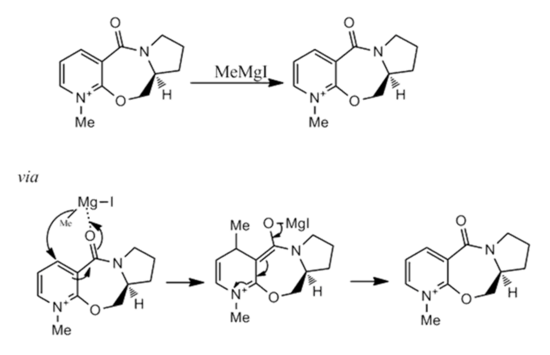
Stereochemistry of Nucleophilic Additions to a pyridinium ring (NAD+ analogue)

The following reactions involving NAD derivatives, examine regio- and stereo- selective nucleophilic attacks at carbon 4 in the pyridine ring. The selectivity of both reactions will be studied by applying MM2 methods to investigate the reactants and their lowest energy conformations.

Nucleophilic attack of Grignard reagent on 5

Molecule 5
Lowest energy conformation

The MM2 force field calculation was carried out on 5 forming the first reactant conformation. The carbonyl group was positioned at an angle of roughly 12°, just above the plane of the aromatic system. The remaining four conformations were derived by manually changing the coordinates of the carbonyl carbon and oxygen. The molecule would manipulate itself so as to lower its energy by adopting positions so as to keep the dihedral angle between the carbonyl and the aromatic plane small, (lowest energy conformation angled approximately at 11°). To try and provoke the molecule, the carbonyl group was positioned below the plane of the ring and the molecule unexpectedly did not reform back to its initial conformation. It was however, extremely high in energy. The main culprit causing the rise in energy was the bend energy, which comes to no surprise. The results show how imperative it is for the molecule to position the carbonyl group above the plane of the aromatic system, especially when considering how much energy it can save by doing so. The Grignard reagent allows coordination of one of the oxygen sp2 lone pairs to the Mg atom, which guides the methyl group to the 4-position in the pyridine ring. The MeMgI reagent could have been included in the calculations if the MOPAC PM6 model was used, but since the calculations were derived by the MM2 method, the appropriate force field parameters are necessary.

Parameter	Conformation 1	Conformation 2	Conformation 3	Conformation 4	Conformation 5
Dihedral Angle /°	11.5664	11.2443	8.2836	-178.47	-178.622
Stretch	2.0393	2.0336	2.0553	13.2062	13.1935
Bend	14.1599	14.2117	14.2997	172.6498	172.8414
Stretch-Bend	0.1347	0.1352	0.1311	-2.5113	-2.4986
Torsion	-5.1991	-5.1365	-5.0457	-1.922	-1.8229
Non-1,4 VDW	-0.595	-0.5761	-0.4573	1.0536	1.0497
1,4 VDW	16.5355	16.5349	16.5673	43.4028	43.3382
Charge/Dipole	9.6561	9.6413	9.5366	11.94	11.9288
Dipole/Dipole	-3.9842	-3.988	-4.0296	-3.0566	-3.0629
Total Energy /kcalmol-1	43.1454	43.129	43.1487	238.6064	238.613
Total Energy /kJmol-1	180.5204	180.4517	180.5342	998.3292	998.3568

A similar quantitative method used to show the preferred carbonyl orientation when attacked by the Grignard's reagent, was used to show the nucleophilic attack by anniline.

Nucleophilic attack of NHPh nucleophile on 7

Molecule 7
Lowest energy conformation

Initially the system seemed to oppose any changes changes imposed to it by readjusting the positions of the atoms. The dihedral angle between the carbonyl and the aromatic ring was then changed itself through the left control panel, and the molecule still managed to manipulate itself to change the angle! The most stable conformation found existed with the carbonyl group just less than 20° below the plane of the pyridine system. This prevents the nucleophilic aniline attacking at the lower face of the ring, since this position is now sterically hindered, which makes it very unfavourable for the relatively bulky nucleophile. Carbon-4 is the preferred, less electron rich position of attack.

Parameter	Conformation 1	Conformation 2	Conformation 3	Conformation 4	Conformation 5
Dihedral Angle /°	-20.6034	-20.2497	-19.7167	84.1402	123.4794
Stretch	3.9482	3.9341	3.9547	6.8224	6.6754
Bend	11.6049	11.5098	11.562	81.104	25.8999
Stretch-Bend	0.4031	0.3985	0.4005	-1.0256	0.6407
Torsion	9.8984	9.7536	9.7252	58.0757	36.1038
Non-1,4 VDW	3.4986	3.5395	3.4665	3.4118	3.1038
1,4 VDW	29.4452	29.4387	29.4141	39.4379	3.1887
Charge/Dipole	9.0043	9.0204	9.0196	-11.8865	0.527
Dipole/Dipole	-4.8856	-4.8867	-4.8837	-4.1778	-4.9907
Total Energy /kcalmol-1	62.917	62.7079	62.6589	171.7619	98.304
Total Energy /kJmol-1	263.2447	262.3699	262.1648	718.6518	411.3039

---

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Antropisomerism can be illustrated by the intermediates of the synthesis of Taxol, 9 and 10. These two molecules arise due to restricted rotation about a single bond owing to the steric demands of the molecule. The difference in the two molecules lies in the orientation of the carbonyl, which is either directed above the molecule ('Up') or below the molecule, ('Down').

9: Lowest energy Conformer
'''9'''

After drawing the chemical structure of 9 in ChemBio3D and performing a MM2 energy minimisation, conformer 1 was generated. The six membered ring was then positioned into a lower energy conformation to try and reduce the energy even further. This was a success, and this was taken as the lowest energy conformer for isomer 9.

10: Lowest energy Conformer
'''10'''

The carbonyl was then positioned facing downwards, and an MM2 calculation found this to reduce the energy from 9. Random atoms were altered to try and reduce the energy even further, but this failed since isomer 10 had already reached its optimal conformation. The remaining manipulations resulted in incremental increases in the energy.

Parameter	Conformation 1	Conformation 2	Conformation 3	Conformation 4	Conformation 5
Relative Orientation of Carbonyl group	Up	Up	Down	Down	Down
Stretch	2.5477	2.5516	2.5678	2.5860	2.5522
Bend	10.5856	10.6888	10.6545	10.6806	10.8092
Stretch-Bend	0.3205	0.3985	0.3173	0.3256	0.3252
Torsion	19.6061	19.5687	19.7462	19.6056	19.6538
Non-1,4 VDW	-1.1103	-1.2063	-1.3263	-1.2371	-1.4440
1,4 VDW	12.5712	12.5595	12.5053	12.5328	12.5750
Dipole/Dipole	-0.1820	-0.1828	-0.1818	-0.1814	-0.1811
Total Energy /kcalmol-1	44.3389	44.3040	44.2831	44.3120	44.2904
Total Energy /kcalmol-1 (MMFF94)	60.5904	60.5669	60.5554	60.5994	60.5611

The energy difference between the lowest conformers of isomer 9 and 10, is 0.209 kJ/mol, so it is a very minor energy difference, which is mainly due to the stretch-bending energy and torsion term. These differences could have arouse since the cyclohexane in 10 exists in its most stable, chair conformation, whereas in 9, it is a higher energy twist-boat conformation due to the carbonyl pointing above the ring system. The larger torsional strain in 10 was a result of the steric and electronic clash between the carbonyl and the bridging iso-propyl group, which is minimised in 9 due to distance between the two groups. The energy difference explains why 9 spontaneously isomerises into the more favourable 10 conformer.

The MMFF94 values are much larger than the corresponding MM2 values, which is due to the use of different force fields. However, both models show the same trend in values for both conformers.

However, the alkene reacts slowly to subsequent functionalisation due to the cage structure of the alkene, which confers stability to the alkene; i.e. hyperstable alkenes. These special types of alkenes are less strained than the parent saturated hydrocarbons, and the bridgehead position of the double bonds mean these alkenes show a reduction in reactivity.

---

Modelling Using Semi-Empirical Molecular Orbital Theory

Molecular Mechanics (MM2) has proved to be useful in estimating the relative energies of molecules and predicting the most probable conformers; however, the approximations and assumptions the model applies are rather crude. One of the key limitations demonstrated by MM2, is that it does not consider electronic influences when calculating energies. For this reason, the semi-empirical Molecular Orbital Theory model (MOPAC, PM6) will be utilised. Not only will this model enhance the derivations, but since it accounts for the electrons, more information can be obtained about our molecule –as illustrated by spectroscopic properties.

Regioselective Addition of Dichlorocarbene

Orbital Control of Reactivity Regioselectivity and reactivity is influenced by the molecular orbitals of the reacting molecules, more specifically, the frontier orbitals (i.e. HOMO and LUMO). This idea is illustrated well via the addition of dichlorocarbene to 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene (12).

Molecular Orbitals of 12

HOMO-1	HOMO	LUMO	LUMO+1	LUMO+2

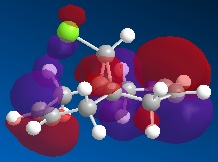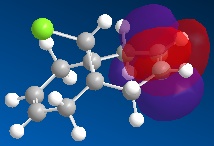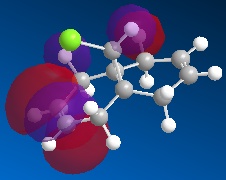Dichlorocarbene is an electrophile, hence, it will attack areas of high electron density. From the above MOs, some key points are evident which will help determine and explain the regioselectivity of the addition to 12 . The HOMO orbital immediately looks very nucleophilic, especially when compared to the HOMO-1 orbital. This can be justified since the HOMO represents the syn-alkene π orbital, which consists of a vast amount of electron density. On the other hand, the relatively electron-poor anti-alkene π orbital (HOMO-1) appears unfavourable for attack by the electrophilic dichlorocarbene. This is further highlighted since the HOMO-1 orbital lies lower in energy than the HOMO, so it would be less likely to react. The stability of the HOMO-1 orbital is reinforced by antiperiplanar interactions between itself and LUMO+1 (C-Cl σ* orbital), meaning that attack by an electrophile to the anti-alkene π orbital is deemed unfavourable. This would only be a possible option if the electrophile used was particularly aggressive, and in which case, both anti- and syn-alkenes would be under attack. This explains why in this specific reaction, the major product is the syn-trichloride and the di-adduct forms as the minor product.

Vibrational Frequencies

The vibrational frequencies of 12 were compared to a hydrogenated derivative, where the anti-alkene bond is replaced by a C-C single bond. Particular focus is made on the Cl-C and alkene bonds, which were obtained using B3LYP/6-31G (d.p) Gaussian geometry optimization and frequency calculation.

Stretching frequencies for tetrahydronapthelene derivatives (cm^-1)

Derivative	Anti-alkene Stretch	Syn-alkene Stretch	C-Cl Stretch
Di-alkene 12	1740.86	1759.11	771.63
Hydrogenated mono-alkene syn-alkene	-	1760.87	774.52
Hydroxy group	1771.29	1766.43	759.81

The calculated vibrational frequencies for all three C=C bonds are significantly higher than the quoted literature value (1640-1680 cm-1), but the C-Cl stretching frequencies correspond well to the literature (760 cm-1). Perhaps the reason for the abnormally high C=C frequency may be because of the calculations and parameters applied. They were calculated based upon an ideal harmonic oscillator, which clearly overestimate the strength of the bonds due to the absence of non-idealities that are evident in reality. To overcome this problem, the calculations should be carried out with a larger basis set to improve accuracy, and if time was not a limiting factor, an anharmonic oscillator model could be applied instead.

The syn-alkene stretch and hence bond energy, remains constant in both adducts, independent of the presence of the anti-alkene bond. Seemingly, the syn-alkene C=C stretches are higher than the corresponding anti-alkene stretch, suggesting that the anti-alkene is less stable due to a smaller bond energy. This contradicts the above speculations aroused from the HOMO and HOMO-1 orbitals, where the anti-alkene π orbital was lower in energy and thus less reactive. However, the molecular orbitals only took into consideration the π-bonds, whereas the stretching frequency accounts for the π and σ-bonds, in the case of double bonds. The destability of the anti-alkene bond due to the σ-bonds can still prevent the electrophile from accessing the π-bond for attack. Addition of a hydroxyl group to the anti-alkene shows a decrease in frequency of the C-Cl stretch, which is due to the lone pairs on –OH, rendering it a donating group, causing an increase in electron density in the anti-alkene bond and in the C-Cl σ* orbital. This would weaken the C-Cl bond, hence showing a decrease in frequency, whilst strengthening the C=C bond resulting in a higher stretching frequency.

N.B –The monohydrogenated dialkene belongs to the Cs symmetry point group and it has a plane of symmetry perpendicular to σh.

Structure Based Mini Project using DFT-based Molecular Orbital Methods

Cocaine (IUPAC name methyl (1R,2R,3S,5S)-3- (benzoyloxy)-8-methyl-8-azabicyclo(3.2.1) octane-2-carboxylate) is a stimulant obtained from the leaves of coca plants, and it is one of four diasteromers. The crystalline tropane alkaloid is infamous for its effects to the human central nervous system, which can lead to physiological addiction to the drug, as well as severe long-term damage to the human body.

This experiment will entail comparisons of computer generated 13C NMR spectra to true spectra carried out by Carroll, Coleman, and Lewin DOI:10.1021/jo00340a004 .They specifically studied the 13C and 1H NMR spectra of cocaine in 1981, and its three diasteromers: pseudococaine, allococaine and allopseudococaine. The objective for this exercise is to examine whether computer based generations of 13C NMR spectra using a TMS mPW1PW91/6-31G(d.p) CDCL3GIAO reference, is adequate enough to verify the true spectra.

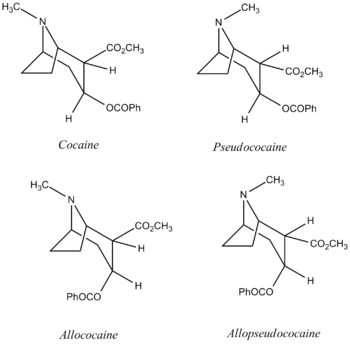
The piperidine ring structure adopts a chair conformation for all four diasteromers, to reduce each of their energies. For cocaine and allococaine, the N-methyl group is shown syn to the ethano bridge, whereas it is anti for pseudococaine and allopseudococaine. Optimisation of all four structures by MM2 force fields and then MOPAC PM6 prior to the 13C NMR calculations produced the following results.

Calculated ¹³C NMR peaks for cocaine, pseudococaine, allococaine and allopseudococaine; NB. 17 C atoms overall, numbering includes the 4 O atoms

Carbon atom	Cocaine shifts (ppm)	Pseudococaine shifts (ppm)	Allococaine shifts (ppm)	Allopseudococaine shifts (ppm)
1	-	-	-	-
2	61.71	61.61	60.99	60.59
3	40.57	27.10	27.27	26.51
4	64.94	28.61	26.52	30.92
5	27.29	35.88	39.06	39.76
6	23.88	63.85	73.21	70.67
7	31.85	47.94	54.48	62.09
8	72.49	66.12	61.93	63.60
9	50.21	-	41.00	167.64
10	168.54	40.60	167.17	-
11	160.51	-	-	40.85
12	-	-	-	-
13	127.21	53.42	51.77	54.88
14	-	53.42	-	-
15	126.47	-	167.79	166.11
16	124.70	126.48	-	-
17	129.71	127.72	127.91	125.35
18	124.69	165.40	129.87	129.43
19	127.68	124.686	125.64	126.93
20	-	129.72	128.44	129.62
21	-	124.90	123.63	124.74
22	51.43	126.88	123.32	125.10

Cocaine
Lowest energy conformation

Pseudococaine
Lowest energy conformation

Allococaine
Lowest energy conformation

Allopseudococaine
Lowest energy conformation

Functional Group	Cocaine Literature	Cocaine Calculated	Pseudococaine Literature	Pseudococaine Calculated	Allococaine Literature	Allococaine Calculated	Allopseudococaine Literature	Allopseudococaine Calculated
NCH3	41.02	40.57	37.36	35.88	41.37	41.00	40.38	40.85
OCH3	51.26	50.21	51.55	53.42	51.65	51.77	51.40	54.88
C=O	170.63	168.54	171.95	165.40	171.80	167.79	171.31	167.64
C=O	166.04	160.51	165.22	129.72	165.41	167.17	165.26	166.11

From the above results, it is evident that the results obtained agree with the literature values. The functional group spectral peaks are also in accordance to literature values, with the only real discrepancy being the second C=O peak for pseudococaine. This value can be improved by taking into account the systematic errors produced by the carbon being attached to the heavy oxygen atom, i.e. δcorr = 0.96δcalc + 12.2. The C=O chemical shift now changes to 136.71 ppm.

The 13C NMR spectra are each characteristic of the corresponding structure it represents, implying that 12C NMR analysis would solely be enough to differentiate each diasteromer. X-ray diffraction could also be used to aid improvements. This experiment has illustrated how useful computational techniques can aid structural assignment and help predict properties of the system. This being said, Carroll, Coleman, and Lewin could have simply used computational methods to carry out their experiment, which would have saved them a lot of time. However, since the paper was published in 1982, such precise and analytical calculations were most likely unavailable at that time, which meant true measurements would have been a necessity. By comparing the calculated spectra to the true spectra, the isomers can be easily and quickly identified.